低采样率高分辨率压缩功率谱估计方法的仿真研究
2016-03-07姚彦鑫
姚彦鑫
(北京信息科技大学,北京100010)
低采样率高分辨率压缩功率谱估计方法的仿真研究
姚彦鑫
(北京信息科技大学,北京100010)
低采样率的宽带功率谱估计在很多领域具有应用价值.采用压缩多核采样结构得到信号的压缩测量值,然后建立测量值相关函数与信号相关函数之间的关系,用最小二乘法实现相关函数估计,最后实现功率谱的估计.该压缩采样方法的等效采样率为M/N·fs,可在没有任何对时域或频域稀疏性的假设条件下降低采样率.仿真分析表明,该方法的系统噪声与加性噪声性能比周期图法略有降低,但只要系统设计合理,对于一定信噪比的信号,系统噪声与加性噪声基本可以忽略,并给出了对应的理论分析.估计分辨率与周期图法相比,等效长度相同时略有提高;由于本文方法降低了测量值的数目,对于一定长度的数据来说,估计分辨率得到了极大的提高.本文方法适用于低信噪比信号的低采样率高分辨率功率谱估计.
功率谱估计;降采样率;自相关;频率分辨率;信噪比
引 言
功率谱密度是随机信号自相关序列的离散傅里叶变换,用来表征随机信号的统计特征,可以用于谐波检测、噪声频谱测量、弱信号检测等.在雷达、声纳、通信、地址勘探、天文、生物医学工程领域具有广泛的应用[1-4].在通信领域可以应用于多载波通信中的解调环节,或者在突发通信模式中进行频率估计,从而保证可靠通信[2].
在高频雷达应用中,通过回波信号的功率谱密度分析可以得到有关目标的各种信息:根据功率谱密度峰值的宽度来判断运动目标的位置;根据峰值的高度判断运动目标的强度;根据峰值的位置来判断目标的运动速度等[5].在雷达信息处理中,多普勒频率估计及多普勒频率域处理是鉴别多目标的一种主要方法[6].在电子对抗领域,雷达信号的频率信息是信号分选、威胁识别、引导干扰的重要参数,如何对截获雷达信号载频进行高精度估计一直是电子战接收机的设计重点.大规模集成电路的发展为数字测频提供了硬件平台,模拟数字混合接收机既可以进行实时处理,也可以将信号存储起来,数字测频的核心在于算法.
信号功率谱的估计方法可分为两类:一为线性估计方法,有自相关估计、自协方差法及周期图法等[7].另一类为非线性估计方法,有最大似然法(MaximumLikelihood,ML)、最大熵法等.线性估计方法的谱分辨率随数据长度的增加而提高,如周期图方法等,然而这类方法在快速高分辨率估计中遇到了困难,难以实现多普勒的高精度估计[5].快速傅里叶变换线性估计方法估计频率也面临频率分辨率与处理数据量之间存在矛盾的问题[8].非线性估计方法大多是无偏的谱估计方法,可以获得高的谱分辨率.ML在所有方法中精度最高,信噪比性能最好,但需要解计算量超高的非线性问题,很多情况无法得到最优解,实时性很差,不适合实际应用.另外两种非线性方法,多重信号分类算法(MultipleSignalClassification,MUSIC)可以达到高的频率分辨率,但在对整个频域内搜索峰值耗时较多,实时性差[3];子空间旋转不变技术 (EstimatingSignalParametersviaRotationalInvarianceTechnique,ESPRIT)计算量比MUSIC小,但是精度没有MUSIC高[4].
实时信号处理希望处理的数据量越少越好,而高的频率分辨率却对数据量提出相反的要求.如果能够降低所需采样数据的数目,同时能够以较高分辨率分辨信号,就成为理想的选择.这方面的文章有基于压缩感知理论构造冗余字典的方法等[9],但此类方法一般需要压缩感知重构算法解算,计算量较大.文献[1, 10]给出一种宽带频谱的功率谱估计方案,其性能分析侧重于宽带谱感知的估计和检测性能方面[11-12].本文则侧重于频点估计的应用,进行了频率分辨率、噪声性能等方面的分析,并给出了在最小稀疏尺度准则的可选方案中,可借鉴的参数方案的选取方法,得到了兼顾采样数据数目、抗噪声性能与频率分辨率的参数方案,为该方法在频率估计中应用提供重要参考.仿真发现该方法在降低采样率的同时,频率分辨率得到提高.至于噪声性能,只要系统设计合理,该方法能够处理一定程度低信噪比的信号.
1 压缩采样
设x(t)是一带宽为1/T的复值广义平稳信号.图1是一个被称为模拟信息转换(AnalogInformationConversion,AIC)的采样装置[1],能够对模拟信号进行压缩采样.该装置有M个分支,第i个分支包含一周期为NT的随机波形调制器和一周期也为NT的积分锁存器,则第i支的第k个输出结果可表示为

(1)
式中,ci(t)是伪随机调制波形一个周期的信号pi(t)乘以1/N.图1实现了对原始信号的压缩,使得观测值含有了原始信号的所有信息.

图1 信号压缩采样框图
在数字仿真模拟数字转换采样过程的平台上,式(1)可表示为

(2)
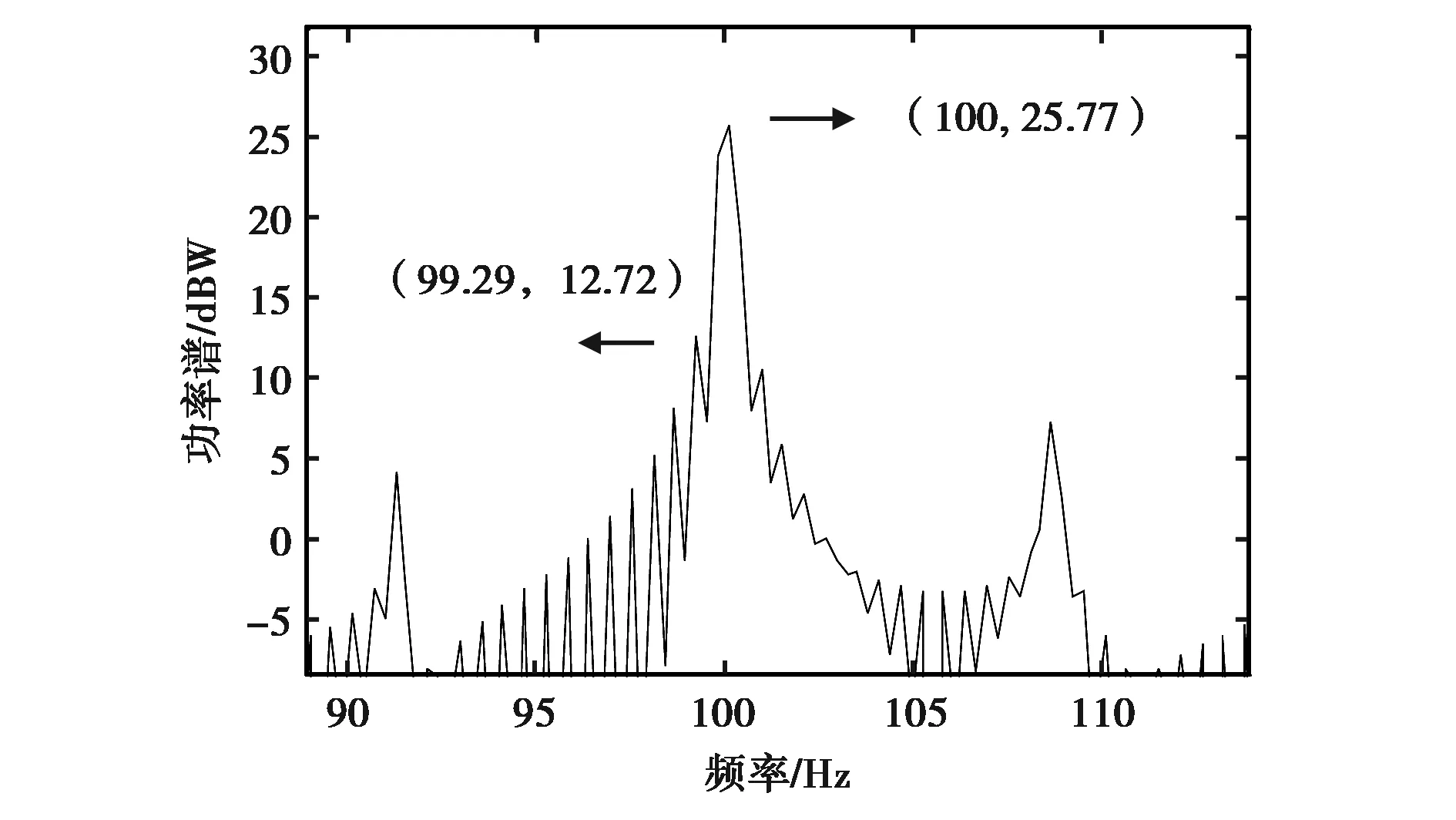
取调制波形为分段常数函数,满足ci(t)=ci[-n],nT 下面基于所获得的{yi[k]}i,k样本,进行x[n]的功率谱重构.x[n]的功率谱或功率谱密度表达式如下: (3) 定义rx(n)=E(x[m]x*[m-n])为x(n)的自相关函数.我们可利用M2个yi[k]与yj[k]的互相关值估计自相关函数rx(n),实现压缩估计而不需要任何关于x(t)的时域或频域稀疏约束条件. yi[k]与yj[k]的互相关表示为 (4) yi是一个对zi的N折叠抽取,即yi[k]=zi[kN]. rzi,zj[n] =rci,cj[n]⊗rx[n] (5) 式中,⊗表示卷积运算.由式(5)可得 (6) 式中: rci,cj[0]= [rci,cj[0],rci,cj[-1],…, rci,cj[-N+1]]T; (7) rci,cj[1]= [rci,cj[N],rci,cj[N-1],…, rci,cj[1]]T; (8) rx[k]= [rx[kN],rx[kN+1],…, rx[(k+1)N-1]]T. (9) rci,cj[l]为ci[·]信号的自相关; 通过级联M2个不同的互相关函数ryi,yj[k],i,j=0,1,…,M-1,得到了M2×1的矢量ry[k]=[…,ryi,yj[k],…]T.根据式(7)、(8)、(9)可推出 (10) 式中,Rc[0]=[…,rci,cj[0],…]T,Rc[1]=[…,rci,cj[1],…]T是M2×N的矩阵.虽然x(n)是带限的,ry会有无限的支撑,但在许多实际应用中,ry[k]只有在-L≤k≤L范围内具较大的值,在此范围外都是可忽略的.又由式(10)知,ry[k]取决于rx[k]与rx[k-1],则可认为rx[k]也需要被限制在-L≤k≤L.那么所有的有效观测量为: (11) (12) 注意以下两点: 1)据上讨论,rx[k]被限制于-L≤k≤L,且rx[n]有复共轭对称性,所以rx[n]被限制在-NL≤n≤NL,rx[L]的最后N-1个值都是0. 2)根据rci,cj[l]的定义,rci,cj[n]被限制在1-N≤n≤N-1,Rc[1]的第一列是0. 这两点使得可以将式(10)中的线性卷积表达为在-L≤k≤L上没有任何额外补零的循环卷积.因此,我们最终将ry以及rx的关系表示为 ry=Rcrx. (13) 式中,Rc是[(2L+1)M2×1]×[(2L+1)N×1]的矩阵, (14) 如果Rc是满列秩的,即要求M2≥N,则式(14)可以利用最小二乘法求解. 最后利用式(15)求出(2L+1)N×1阶的能量谱矢量Sx: =F(2L+1)Nrx. (15) 式中,F(2L+1)N是(2L+1)N×1的离散傅里叶矩阵. 为了保证最小二乘(Least Squares,LS)解的唯一性,随机调制波形可以有很多不同的实现方法,如高斯抽样、贝努力抽样等.研究如何选取随机调制波形,才能在保证估计性能的条件下,使支路的数目M尽量小. 本文采用最小稀疏尺度抽样多核实现方法.该方法基于最小稀疏尺度问题,可以通过简单地设置ci[n]来实现,对于不同的i,设置不同的ci[n].ci[n]=1如果-n=ni;ci[n]=0,如果-n≠ni,其中i≠j时,ni≠nj. 以上ci[n]的设置方法也可以由从单位阵IN中选择M个不同的行实现.然而,注意到这种行的选择不会是随机的,因为我们要保证式(14)中Rc的列满秩性,其实只需保证Rc中每列至少有一个1. 而由自相关函数的对称性和式(7)、式(8)知,如果Rc[0]对应于前[N/2]+1列至少有一个1,那么对应地,Rc[1]于后[N/2]列至少有一个1,[x]表示不大于x的最大整数.因此,问题成为选择IN的行组合,保证Rc[0]在其前[N/2]+1列至少有一个1.为了最小化压缩比M/N,希望M尽量小. (16) 式中,|S|表示集合S的势. 尽管式(16)可通过穷举或贪婪搜索法求解,但运算量太大.一个可能找到式(16)次优解的方法是通过解所谓的最小长度[N/2]稀疏尺度问题,该问题已经在文献[13-14]中被很好地研究.表1中是一些符合最小稀疏准则的可选M、N对的取值. 本文方法的优点是将N个采样点压缩为M个支路的测量值,压缩比为M/N,达到压缩功率谱估计的目标.并且直接在模拟域实现信号变换,而后进 表1 最小稀疏准则的例子 行压缩采样,大大降低了数字信号的采样率和处理复杂度,求解的时候,除了必要的傅里叶变换矩阵转换,即时域与频域的转换外,只用到了LS方法,避开了压缩感知恢复算法等复杂的运算环节,是功率谱估计一个可选方法.因此,本方法中只需要满足M2≥N和Rc矩阵的列满秩,即成为过定方程,可用最小二乘法求解. 4.1 分辨率性能分析 功率谱估计的分辨率是分辨两个频率相近的正弦(或窄带)信号的能力,常用功率谱的主瓣宽度来度量,即主瓣在半功率点处的半边宽度. 仿真方案:信号为单频信号x=10cos(2πf0t),最小稀疏尺度抽样多核采样方案,参数选取为(M=6、N/2=13),随机调制波形的码速率是1/T=800 Hz.周期图法中,参数为fs=800 Hz.为了方便比较,两种方法处理信号的时间长度均为N(L+1)T.对于同样时间的采样数据,采样数目不同,周期图法是N(L+1),本文方案是M(L+1). 两种方法分别对参数f0=100 Hz、200 Hz、300 Hz,L=5、10、20、30的每对组合进行100次试验.统计本文方法和周期图法功率谱估计分辨率的平均值,如表2所示.图2为某次实验中周期图法的频率分辨率的计算示意图. 表2 两种估计方法的频率分辨率对比(M=6、N/2=13) 图2 周期图法的频率分辨率L=30 由表2可知:在同样测量数目的情况下,本文方法的分辨率明显高于周期图法;而对于同样的等效数据长度,本文方法的分辨率也略高于周期图法. 为了比较最小稀疏尺度抽样多核采样方案在不同参数设置下分辨率的情况,选取L=20,对于f0=100 Hz、200 Hz、300 Hz,不同的采样方案(M、N/2)分别进行100次试验,统计分辨率如表3所示.观察得到当L一定时,最小稀疏尺度抽样多核采样方案使用实际数据的长度越长,分辨率越高. 周期图的频率分辨率严格与所使用数据的长度成反比[15].而本文方法当(M,N/2)取值一定的时候,分辨率随着L长度的增加而近似成反比例规律提高,如表2所示.实验结果不成严格反比关系可能是因为仿真次数较为有限,结果存在一些偏差.本文方法当L取值一定,参数(M,N/2)变化时,分辨率与等效数据长度表现出类似于反比例的关系,如表3所示. 表3 最小稀疏尺度抽样多核采样方案在不同参数方案的频率分辨率的对比 4.2 噪声条件下性能分析 衡量抗系统噪声性能指标的实验方案:取有用信号为x=10·cos(2πf0t).为考察最小稀疏尺度抽样多核采样方案的噪声性能,以L=30,(M=8,N/2=23)为例,1/T=800 Hz,那么测量数据长度为(L+1)M,等效数据长度为(L+1)N.周期图法采样率也为800 Hz,采样数据长度为(L+1)N.未在有用信号x上添加噪声时,计算有用频率处的谱峰值是p,代表有用信号的功率;计算其他位置处谱峰的最大值是q,代表该频率处的系统噪声功率,衡量抗系统噪声性能用10log2(p/q)dB.如图3(a)一次试验的局部图所示,抗系统噪声性能为13.05 dB. 为了验证最小稀疏尺度抽样多核采样方案取不同最小稀疏尺度时的有效性和抗噪声性能,随机选用0~400 Hz之间的单频点作为f0,用不同随机波形的选取方法,反复进行实验,得到抗系统噪声指标的平均值.为了公平,每组参数的第二次试验中,调整L使得等效的数据长度即(L+1)N接近相同. 由表4可见,除了(M=5,N/2=9)组合外,基本上抗自噪声性能都在13 dB左右.那么,综合压缩比的因素,得到M=8,N/2=23时,信号的压缩比与系统自噪声性能都相对较好.观察得到新方法的抗自噪声性能随着信号数据增加,没有明显改善.这与传统周期图法的规律是不同的.考虑主要是由于方法在L=30时数据自相关信息已经基本包括,L不需要取得更长. (a) 局部图 (b) 全局图图3 压缩功率谱估计系统噪声性能 (L=30,M=8,N=46) 周期图法的抗系统噪声性能:f0从0~400 Hz随机选取,采样率800 Hz,统计100次试验中最大相邻旁瓣与峰值之差的平均值得到抗系统噪声性能,在18 dB左右,较为理想.f0=100 Hz的示例如图4所示. 衡量抗加性噪声性能的实验方案:有用信号x=a·cos(2πf0t),在有用信号x基础上添加了加性噪声,该加性噪声是均值为0、方差为σ2的限带高斯白噪声,噪声覆盖带宽为0~800 Hz.周期图法采用fs=800 Hz,使用了(31·N)的采样数据长度.多核采样方法参数采用M=6、N/2=13、L=30. 图4 周期图法的抗系统噪声性能 M[N/2]L选择的尺子抗系统干扰性能/dB3330116[0,1,3]14.9613.15593043[0,1,2,5,9]8.909.006133053[0,1,4,5,11,13]13.1013.2182330[0,1,2,11,15,18,21,23]13.00 两种方法都随机选用0~400 Hz之间的单频作为f0,当正弦信号幅度a和噪声方差σ2取不同值时,反复进行Monte Carlo实验,得到的抗加性噪声性能如表5所示.将两种方法得到的功率谱有用频率处谱峰值,与代表加性噪声最大谱峰值的比值作为抗加性噪声性能指标. 表5 两种方法的抗加性噪声性能对比 从表5可以看出,新方法相比于周期图法,其抗系统噪声性能略有降低.这是因为经过理论推导,发现周期图法等效于使用自相关函数加上三角Bartlett窗来计算功率谱[15],而新方法相当于使用自相关函数加上近似为矩形的窗来估计功率谱.由于抗系统噪声性能主要取决于所使用窗函数第一旁瓣与主瓣的高度比值,而两种方法分别使用的窗函数频谱的主瓣与第一旁瓣比值为:矩形窗约为9dB,Bartlett窗为17dB.这个理论分析的结果与表5中仿真得到的两种方法的平均抗系统噪声11.80dB和18.48dB基本吻合. 两种方法的抗加性噪声的性能随信噪比的降低而减弱.新方法的抗加性噪声的性能并没有随着噪声强度变化成正比变化,这是因为根据式(10),当x(t)包括噪声时,估计自相关中会包括无噪信号的自相关、噪声自相关与无噪信号和噪声的互相关三项.仿真发现,由于所使用估计信号长度有限,限带“白噪声”的互相关也并不是完美地为“0”,加上噪声与信号的互相关项的影响,使得估计出来的自相关函数随着噪声能量的增加,并不呈现明显的线性关系.自相关函数再经过傅里叶变换得到功率谱(见式(15)),则新方法的抗加性噪声性能,虽然具有单调性,但呈现出较为复杂的非线性关系,如表5所示. 虽然新方法的抗噪声性能不如周期图法,但能够降低采样数据的数目,且分辨率佳.新方法的测量值数目压缩比可高达0.27.另外,新方法的频率分辨率不随测量数据长度的减少成正比例关系下降,降低较少,抗噪声性能在大多数应用场合能够适应.因此,对于很多应用,最小稀疏尺度抽样多核采样方案是具有实用性的,可以达到对一定程度低信噪比的信号在总数据处理量增加不多的前提下,提高频率分辨率的效果. 1) 本文方法能够在对时域和频域都没有稀疏性假设条件的前提下,以较低的采样率,实现低信噪比信号的功率谱估计. 2) 系统的噪声性能,包括系统噪声与加性噪声,主要取决于系统参数.系统噪声虽然较大,但通过对基于最小稀疏尺度准则的采样结构的研究,发现只要参数设计合理,就能够完全克服这个问题;当选取参数合理时,抗加性噪声性能也可以接受. 3) 本文方法的估计分辨率与相同等效长度的周期法相比,分辨率略有提高;由于本文方法降低了测量值的数据长度,那么对于一定长度的测量数据来说,估计分辨率得到了极大的提高. 4) 对于基于最小稀疏准则的多核采样方案,如何设计参数能够取得更好的性能还有待进一步研究. [1] ARIANANDA D D, LEUS G. Compressive wideband power spectrum estimation[J]. IEEE transactions on signal processing, 2012, 60(9): 4775-4789. [2] 石盛超, 索龙龙, 张卫同. 基于自相关函数的前向频率估计方法综述[J].电子质量, 2012(12):38-42. SHI S C, SUO L L, ZHANG W T. Autoeorrelation-based feedforward carrier frequency estimator[J]. Electronics quality, 2012(12):38-42. (in Chinese) [3] 蒋琼. 基于MUSIC算法的电力谐波、间谐波频谱估计方法研究[D]. 长沙:长沙理工大学, 2012. JIANG Q. The research of spectrum estimation for the electrical harmonic and interharmonic based on MUSIC algorithm[D]. Changsha: Changsha University of Science & Technology, 2012. (in Chinese) [4] 司伟建, 蓝晓宇, 刘学. 提高二维DOA估计分辨率的改进MUSIC算法[J]. 西安电子科技大学学报(自然科学版), 2012, 39(2):138-144. SI W J, LAN X Y, LIU X. Modified MUSIC algorithm for improving the resolution of 2-D direction of arrival estimation[J]. Journal of Xidian University(natural science), 2012, 39(2): 138-144. (in Chinese) [5] 梁宏光. 基于压缩感知的频率估计技术的研究[D]. 哈尔滨:哈尔滨工业大学, 2013. LIANG H G. Research on frequency estimation on techniques based on compressed sensing[D]. Harbin: Harbin Institute of Technology, 2013. (in Chinese) [6] 刘银恩. 高精度频率估计算法研究[D]. 南京: 南京理工大学, 2007. LIU Y E. Study on high precision frequency estimation algorithm[D]. Najing: Nanjing University of Science and Technology, 2007. (in Chinese) [7] 单凉, 王伟, 黄超. 列车测速中多普勒频率估计方法研究[J].电子技术, 2016, 45(2): 1-5. SHAN L,WANG W, HUANG C. Train speed estimation method of Doppler frequency [J]. Electronic technology, 2016, 45(2):1-5. (in Chinese) [8] 黄翔东, 王越冬, 靳旭康, 等. 无窗全相位FFT/FFT相位差频移补偿频率估计器[J]. 电子与信息学报, 2016, 38 (5): 907-912. HUANG X D, WANG Y D, JIN X K, et al. N o-windowed apFFT/FFT phase difference frequency estimator based on frequency-shift & compensation[J]. Journal of electronics & information technology, 2016, 38 (5): 907-912.(in Chinese) [9] 沈志博, 董春曦, 黄龙, 等. 一种基于稀疏分解的窄带信号频率估计算法[J]. 电子与信息学报, 2015, 37(4): 907-912. SHEN Z B, DONG C X, HUANG L, et al. A frequency estimation algorithm of narrow-band signal based on sparse decomposition[J]. Journal of electronics & information technology, 2015, (4):907-912. (in Chinese) [10]LEUS G, ARIANANDA D D. Power spectrum blind sampling[J]. IEEE signal processing letters, 2011, 18(8): 443-446. [11]卢光跃, 弥寅, 包志强, 等. 基于特征结构的频谱感知算法[J]. 西安邮电大学学报, 2014, 9(2): 1-10. LU G Y, MI Y, BAO Z Q, et al. Cooperative spectrum sensing algorithms based on eigenvalue structure of the received signal[J]. Journal of Xi’an University of Posts and Telecommunications, 2014, 19(2): 1-10. (in Chinese) [12]刘学谦. 支持向量机在频率估计算法中的应用研究[D]. 郑州: 解放军信息工程大学, 2014. LIU X Q. Research on application of support vector machoine in frequency estimation algorithm[D]. Zhengzhou: The PLA Information Engineering University, 2014. (in Chinese) [13]Sparse ruler [EB/OL]. [2016-08-20]. https://en.wikipedia.org/wiki/Sparse-ruler, 2013. 01. [14]LEECH J. On the representation of 1, 2… n by differences[J]. Journal of the London Mathematical Society, 1956, 31: 160-169. [15]姚天任, 江太辉. 数字信号处理[M]. 2版. 武汉: 华中科技大学, 2000. Simulation on low sampling rate high resolution compressed power spectrum estimation method YAO Yanxin (BeijingInformationandScienceTechnologyUniversity,Beijing100010,China) Low sampling rate power spectrum estimation could be applied in many domains. In the paper, firstly the compressed multi-coset sampling structure is adopted to obtain the compressed measuring values, and the relationship between correlation of measuring values and autocorrelation is built. Secondly, the estimation for signal autocorrelation is realized using least squares. At last, the power spectrum estimation is realized through frequency domain transformation. To reduce the compression rate, the realization structure based on minimal sparse rule is studied. The equivalent sampling rate for the method isM/N·fs, which enables low sampling rate spectrum estimation without any sparse assumptions about the frequency or time domain signals. Through simulations, it proves that the system noise and additive noise performance is not as good as periodogram method. But if system design parameters are properly designed, the noise could be ignored. The corresponding theoretical analysis is given as well. The frequency resolution performance is improved compared to periodogram method, however, the method reduces the number of measured data, so for certain measured data, the frequency resolution performance is elevated greatly. Thus, the method is applicable to the low sampling power spectrum estimation of low SNR signals. power spectrum estimation; low sampling rate; autocorrelation;frequency resolution;signal-to-noise ratio 10.13443/j.cjors.2016082001 2016-08-20 国家自然科学基金(61302073);北京市自然科学基金(4172021);北京市教委面上项目;北京市自然科学基金(Z160002) TP391 A 1005-0388(2016)06-1172-08 姚彦鑫 (1982-),女,河北人,副教授,硕士生导师,研究方向为卫星导航、认知无线电. 姚彦鑫. 低采样率高分辨率压缩功率谱估计方法的仿真研究[J]. 电波科学学报,2016,31(6):1172-1179. YAO Y X. Simulation on low sampling rate high resolution compressed power spectrum estimation method [J]. Chinese journal of radio science,2016,31(6):1172-1179.(in Chinese). DOI: 10.13443/j.cjors.2016082001 联系人: 姚彦鑫 E-mail: yanxin_buaa@126.com DOI 10.13443/j.cjors.20160820012 功率谱估计的时域重构方法
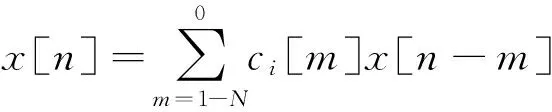


3 最小稀疏尺度抽样方案

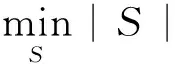

4 压缩功率谱估计方法的性能







5 结 论
