基于有限元方法的凸齿镇压器运动学和动力学分析

张智泓，张广凯，佟 金，Stephen Carr，赖庆辉，张兆国， 方秋容

(1.昆明理工大学现代农业工程学院，云南昆明 650500；2.吉林大学生物与农业工程学院，吉林长春 130025；3.吉林大学工程仿生教育部重点实验室，吉林长春 130025；4.International Soil and Water Renewables，LLC，Indiana Salem 47167 US)



基于有限元方法的凸齿镇压器运动学和动力学分析

张智泓1，张广凯1，佟 金2，3，Stephen Carr4，赖庆辉1，张兆国1， 方秋容1

(1.昆明理工大学现代农业工程学院，云南昆明 650500；2.吉林大学生物与农业工程学院，吉林长春 130025；3.吉林大学工程仿生教育部重点实验室，吉林长春 130025；4.International Soil and Water Renewables，LLC，Indiana Salem 47167 US)

摘要为探索凸齿镇压器在作业过程中的运动学和动力学特性，基于验证有效性后的有限元模型，求解了凸齿镇压器外缘点运动轨迹和速度以及加速度随时间的变化规律曲线。结果表明：轮缘点所在凸齿冲击土壤的行为并未在轮缘点竖直方向速度最大时完成；凸齿镇压器轮缘外一点的绝对运动轨迹呈波动状态的余摆线形式；凸齿镇压器轮缘点在接地位置有与前进方向相反的相对滑动。

关键词凸齿镇压器；土壤表面微形貌加工；有限元方法；运动轨迹求解；运动学和动力学分析

土壤表面微形貌加工是近年来在干旱与半干旱耕作区得到快速发展的一种整地方式。在地面机械领域，研究横轴类旋转工作触土部件的工作机理时，探索工作部件特征点的运动轨迹曲线是分析机具正常工作的条件及其量化指标的重要研究内容[1-3]。目前，求解机具旋转工作部件运动轨迹主要依靠经典力学的基础理论推导，然而使用基础理论求解凸齿镇压器轮缘点运动轨迹具有如下局限性：分析过程中需要做大量简化，与实际作业条件有一定的偏离；与地面相互作用时，受到垂直载荷、凸齿形状、牵引速度等参数的影响；土壤流动变形特征具有复杂本质，导致一些工作参数难以测量。随着计算机计算能力的逐步提高，借助于计算机应用有限元等数值方法求解机械对土壤加工的典型工艺问题增多，有限元分析方法成为分析土壤与农机触土部件相互作用规律的有效工具。为了揭示凸齿镇压器的轮缘点运动特征和运动学特性，笔者基于有限元方法，对凸齿镇压器工作过程中轮缘点的轨迹及其运动学特征进行求解和分析，旨在为提高凸齿镇压器的工作性能和作业质量提供理论基础。

1材料与方法

1.1土壤表面微形貌加工原理土壤表面微形貌加工原理如图1所示，通过在田间土壤表面加工出若干规则微坑阵列以改变地表微观地形地貌，从而拦蓄降水产生的田间地表径流[4]。通过该整地措施，地表径流得以汇集并渗入土壤内部，不仅有效地控制过量降水造成的水土流失，还把雨水转化为土壤水，使水分富集于地表土壤以供作物生长利用，从而趋利避害，在降低过量降水对农业生产的负面影响的同时集蓄降水，使其对作物生长产生积极作用，最大限度地提高天然降水的利用效率，达到控制水土流失和缓解干旱缺水的双重目标[5-7]。

凸齿镇压器是实现土壤表面微形貌加工作业的新型特殊滚动触土部件。该机具圆柱面上均匀分布凸齿，凸齿形状为4个端面为斜角的棱柱，凸齿镇压器机具作业时，由牵引机具以一定速度牵引并在田间土壤表面滚动，滚动时凸齿挤压地表土壤，使地表土壤流动和变形，在田间地表加工出几何形状规则的微坑形貌[8-9]。在凸齿镇压器加工地表微形貌的过程中，其非圆形轮廓在滚动时重心呈周期性的交替升高和下降，凸齿镇压器的势能和动能周期性转化为冲击能作用于地面，凸齿镇压器的轮缘点运动轨迹、速度、加速度等因素影响着工作效率和作业质量。

注：a为土壤表面微形貌加工过程；b为微坑蓄水示意。Note：a.Process of micro-topographical preparation；b.Diagram of water storage in micro-basin.图1　土壤表面微形貌加工原理Fig.1　Principles of micro-topographical preparation

而在农业机械领域，旋转工作触土部件可归纳为驱动式和牵引式，由于工作原理不同，其工作部件的运动情况也不同。对于非驱动牵引式旋转工作部件，如旋耕机，工作时刀片一边绕轴正向旋转，一边随机组做直线运动，因此，刀片的绝对运动轨迹是一条由旋转运动与直线运动合成的数学摆线。数学摆线形式由机组前进速度和机具旋转角速度两个参数同时决定，由于二者之间的数值及其组合不同，其合成后的摆线形状存在较大差异，摆线形式可分为短摆线、滚摆线、余摆线，并且对旋耕机最终的工作结果产生不同影响。对于非驱动牵引式旋转工作部件，如传统刚性轮，在地面做无滑动滚动时其轮缘外一点的运动轨迹是标准滚摆线形式[10-11]。然而，凸齿镇压器与其他牵引式典型圆形工作轮[12-14]有本质区别，凸齿镇压器为非圆形工作轮，运动时其质心呈周期性的升高和下降，故作业过程中对土壤产生冲击作用，具有冲击压实的效果。另外，与刚性轮在地表做无滑动滚动不同的是，凸齿镇压器在土壤表面工作时，工作情况具有复杂特性，一方面，土壤为弹塑性材料，凸齿镇压器在土壤表面工作的过程中土壤会发生变形；另一方面，凸齿镇压器与土壤的接触界面存在滑动摩擦。1.2凸齿镇压器工况设置凸齿镇压器与土壤相互作用时的工况如图2所示。相对运动：凸齿镇压器外缘的一点M相对于凸齿镇压器的中心RP做旋转运；牵连运动：凸齿镇压器中心RP被牵引机构牵引，在水平方向向前运动；在加工微坑过程中，凸齿镇压器在竖直方向载荷与水平方向牵引力的作用下，不断嵌入土壤并被抬起，因此凸齿镇压器中心RP在竖直方向上做往复运动。

图2　凸齿镇压器工况Fig.2　Working condition of toothed wheel

1.3有限元模型尺寸和边界条件凸齿镇压器与土壤作用模型如图3所示。L为模拟土槽的长度，尺寸设置为2 500 mm；W为模拟土槽的宽度，尺寸设置为200 mm；H为模拟土槽的高度，尺寸设置为250 mm。凸齿镇压器以1 000 mm/s的速度沿X轴向前运动2 000 mm。为了使凸齿镇压器各单元的牵引力集中计算输出，设定凸齿镇压器滚动轮旋转中心为整个凸齿镇压器的刚性参考点(RP)。将土体模型底面设定为全局约束，限制底面的全部6个自由度，将通过原点的YZ平面设为对称面，土体模型的上表面不做约束。参考点RP沿水平方向以固定速度运动，时沿竖直方向自由移动，轮缘点M绕参考点RP做圆周运动，同时做以上几种运动的合成运动。由于该模型为几何对称型，为提高计算效率，采用沿对称面分割的半个模型进行模拟，但输出结果为完整模型的结果。

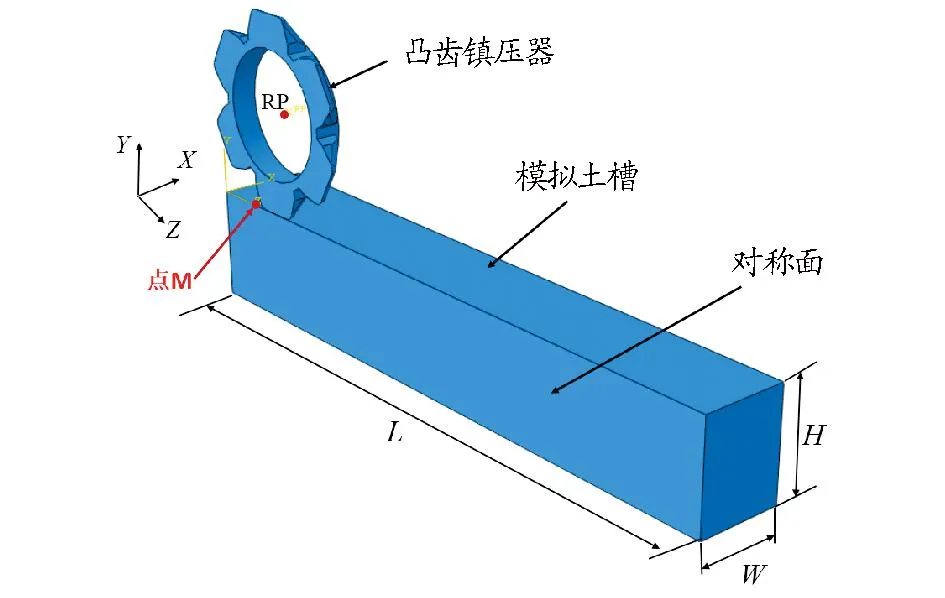
图3　土壤模型Fig.3　Size of soil bin model

1.4凸齿镇压器的尺寸凸齿镇压器的尺寸(图4)为目前被广泛采用的凸齿镇压器设计尺寸[4]，其中D和d分别为凸齿镇压器滚动轮的外径和内径，尺寸分别为340和300 mm，U为凸齿镇压器的滚动轮宽度，尺寸为115 mm。凸齿镇压器上沿圆周均匀分布有6个凸齿，每个齿为三角棱形状，凸齿宽度z为90 mm，凸齿高度y为70 mm，凸齿底部长度b为150 mm，凸齿顶部长度t为100 mm。

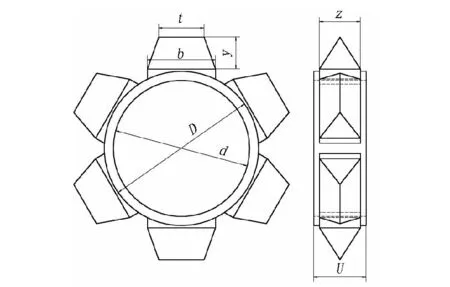
图4　凸齿镇压器模型Fig.4　Size of toothed wheel model

1.5有限元模型网格在有限元模型的建立过程中，有限元网格划分的质量直接影响计算的精度和速度。在进行网格划分时，首先确定单元类型。模拟土槽模型的网格采用八节点缩减积分实体单元C3D8R，该类型的单元常被用于连续材料的三维应力应变分析，土壤模型单元尺寸设置为8 mm，节点总数为261 248，单元总数为242 575。凸齿镇压器模型作为离散刚体导入有限元软件，其网格采用三维四面体单元C3D4，单元为9 mm，节点总数为5 781，单元总数为25 006。

1.6模型运行计算机环境有限元模型的计算求解在吉林大学工程仿生教育部重点实验室的工作站进行。工作站型号：戴尔Precision T7500(CPU型号：E5645，CPU主频：2.4 G，内存容量：8*DDR3)。

1.7有限元模型的有效性验证基于前期研究结果[8]，为了验证模型的准确性，在吉林大学工程仿生教育部重点实验室土槽实验室进行验证实验。选择牵引力和土壤流动变形结果作为验证参数，基于室内土槽测试系统搭建牵引实验平台(图5)，在载荷为250 N，牵引机构运行速度为1 m/s的作业条件下，考察实际实验与有限元分析的误差。通过比较有限元与土槽实验求解的牵引力与时间的关系曲线，发现2条曲线变化规律一致；比较牵引力平均值，计算得到相对误差为3.40%，证实有限元分析结果达到所需精度；同时，将有限元方法求解得到的微坑形貌与土槽实验结果比较，结果表明有限元方法预测的微坑外部和内部的形貌特征与实测实验一致。因此，笔者所建立的有限元模型可有效地模拟凸齿镇压器与土壤间的相互作用。

图5　牵引实验平台Fig.5　Test platform of draft force

2结果与分析

2.1场变量输出结果模型连续求解时间合计260 h，运行完成后，场变量输出结果如图6所示。土壤模型网格规整，未出现网格单元过渡扭曲现象。

2.2轮缘点运动轨迹曲线求解所得点M(图6)的绝对运动轨迹如图7所示。与刚性轮在地表做纯滚动的标准旋轮线运动轨迹不同，凸齿镇压器在土壤表面运动时，由于凸齿镇压器圆周上的凸齿依次压入土壤和抬离地面，凸齿外缘点M的运动曲线并非光滑曲线，而是呈规律的波动状态。施加竖直向下载荷后，点M在0~40 mm位置有一个向下的位移，对点RP施加水平速度后，随着凸齿镇压器的向前运动，凸齿被抬起，点M向上移动，在800 mm位置处运动至最高点，完成提升过程；此后开始向下移动，在1 400 mm位置处，点M的竖直方向位移已为负值，此时点M位置的凸齿已开始贯入微坑；点M在1 450 mm位置运动至最低点并到达微坑的底部，完成冲压过程。在图6的框中放大区域位置，点M有一定的向后移动距离，在此处凸齿压入土壤，然后随着凸齿镇压器继续向前运动凸齿再次被抬离，进入下一个工作周期。

图6　场变量输出结果Fig.6　 Result of field ouput

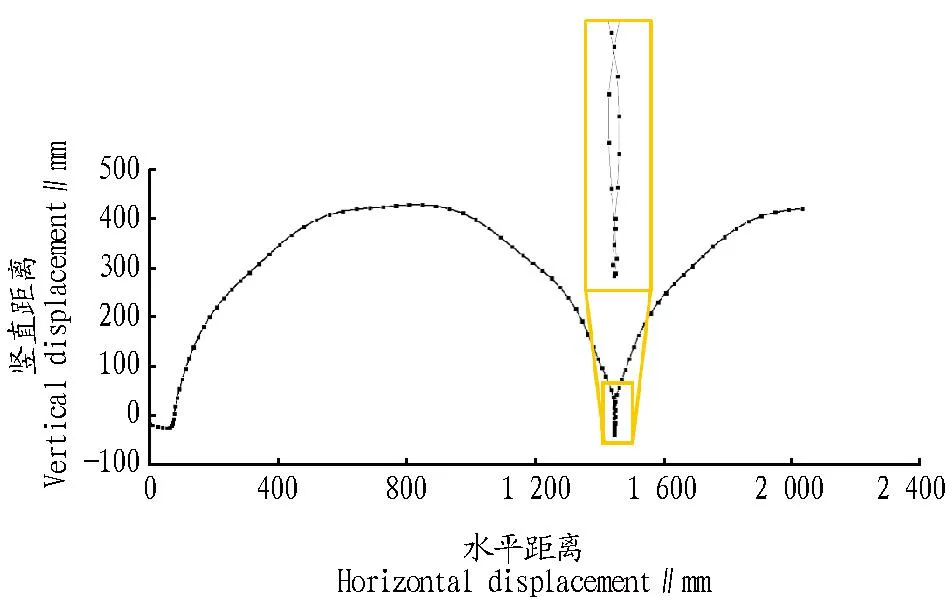
图7　凸齿镇压器轮缘点的运动轨迹Fig.7　Motion trail of toothed wheel outer edge point

为进一步揭示凸齿镇压器的运动轨迹规律，将点M的合位移分解为沿水平和竖直方向的分位移。如图8所示，凸齿镇压器运动开始后，点M在竖直方向向上移动的过程中，水平方向位移也在增加；点M在0.9 s时到达最高点，此后迅速向下移动；在1.5 s时，点M竖直方向位移值为负，此时点M已开始贯入微坑，并在1.6 s时运动至最低点；点M运动到最低点后，水平方向位移曲线趋于平缓并有一定程度的下降，此时凸齿压入微坑最底端，说明凸齿与微坑底部在水平方向有一定的相对滑动；在1.7 s时，点M竖直方向位移转换为正值，此时点M所在凸齿已从微坑中抬离。

2.3轮缘点速度随时间变化曲线的求解分别对点M在水平方向和竖直方向的速度分量随时间的变化曲线进行求解。从图9可以看出，点M在0.9 s达到最高点之前，其所在的凸齿属于提升过程，水平方向速度分量不断增加，而竖直方向速度分量先增加后减小，并在0.9 s位置为0；点M在0.9 s达到最高点之后，其所在的凸齿进入冲击过程，水平方向速度分量逐渐减少，竖直方向分量沿相反的方向逐渐增大，即点M在向下做加速运动，在1.3 s位置点M竖直向下的速度达最大值。然而，点M所在凸齿冲击土壤的行为并未在其速度最大时完成，这是由于其所在凸齿开始冲击土壤的同时也是前一个凸齿从土壤中抬起的过程，该过程阻碍了点M所在凸齿的向下运动，从而减小了其竖直向下的速度。而点M在1.5 s和土壤接触时仍具有较高的竖直向下速度，因此冲击作用明显。冲击发生后，点M在竖直方向的速度变化有一定减缓，此时点M所在凸齿贯入微坑，在水平方向上的速度为最低点，随后出现正负交替，同样说明此时点M在水平方向上与土壤有相对滑动。2.4轮缘点加速度随时间变化曲线的求解为更加直观地观察水平方向和竖直方向加速度分量随时间的变化情况，分别对点M在水平方向和竖直方向的加速度分量随时间的变化曲线进行求解。从图10可以看出，冲击发生的1.4 s前的瞬间，点M竖直方向加速度为正，说明此前点M竖直向下的速度在逐渐减小；冲击发生后，点M竖直方向加速度为0，说明此时点M有一段匀速运动过程；冲击完成后，点M加速度迅速增大，说明此时点M贯入微坑过程中向下运动的速度迅速减小；最终，点M离开微坑时向上做加速运动。

注：a为水平方向的运动轨迹；b为竖直方向的运动轨迹。Note：a.Motion trail at horizontal direction；b.Motion trail at vertical direction.图8　凸齿镇压器轮缘点在不同方向的运动轨迹Fig.8　Motion trail of toothed wheel outer edge point at different directions

注：a为水平方向的运动速度分量；b为竖直方向的运动速度分量。Note：a.Velocity at horizontal direction； b.Velocity at vertical direction.图9　凸齿镇压器轮缘点在不同方向的运动速度分解Fig.9　Velocity of toothed wheel outer edge point at different directions

注：a为水平方向的运动速度分量；b为竖直方向的运动速度分量。Note：a.Velocity at horizontal direction；b.Velocity at vertical direction.图10　凸齿镇压器轮缘点在不同方向的运动加速度分解Fig.10　Velocity of toothed wheel outer edge point at different directions

3结论与讨论

笔者使用有限元方法求解了凸齿镇压器轮缘上一点的运动轨迹，以及该点速度、加速度不同方向的分量随时间的变化情况，结果表明：①从绝对运动轨迹随时间变化曲线可以看出，凸齿镇压器轮缘外一点的绝对运动轨迹为非光滑曲线，表现为呈波动状态的余摆线形式；②从轮缘点位移与速度随时间变化曲线可以看出，轮缘点运动到最低点时，凸齿压入微坑最底端，水平方向位移曲线趋于平缓并有一定程度的下降，同时观察到轮缘点在水平方向上的速度矢量出现正负交替，证实凸齿镇压器轮缘点在接地位置有与前进方向相反的相对滑动；③从速度与加速度随时间变化曲线可以看出，冲击发生前的瞬间，轮缘点竖直方向加速度为正、方向向上，说明此前轮缘点竖直向下的速度逐渐减小，轮缘点所在凸齿冲击土壤的行为并未在轮缘点竖直方向速度最大时完成，这是由于轮缘点所在凸齿开始冲击土壤的同时也是前一个凸齿从土壤抬离的过程，该过程阻碍了轮缘点所在凸齿的向下运动，从而减小了轮缘点竖直向下的速度。

该研究揭示的基本信息和科学规律为今后凸齿镇压器的研究提出如下思路：一方面，充分利用凸齿镇压器轮缘和土壤的相对滑动现象改变凸齿刃口结构，如将平滑刃口改为锯齿结构刃口，从而将滑切方式改为锯切方式，以减小凸齿贯入土壤的阻力，并增加所加工微坑的深度；另一方面，改变凸齿沿轮缘排列方式或改变凸齿外缘轮廓几何结构，以使凸齿冲击土壤的行为在轮缘点速度最大时完成，从而提高所加工微坑的质量和效率。

参考文献

[1] 何岳平，陈青春，何瑞银，等.以穴宽为优化目标的大蒜栽植机关键机构运动仿真及优化设计[J].安徽农业科学，2009，37(36)：8161-8164，8179.

[2] 张华标，朱梅，朱德泉，等.高速水稻插秧机分插机构振动特性研究 [J].安徽农业科学，2012，40(18)：9906-9907，9919.

[3] 赵志国.吊篮-鸭嘴式移栽机栽植器运动轨迹分析[J].安徽农业科学，2011，39(19)：11932，11935.

[4] PATRICK C，KECHAVARZI C，JAMES I T，et al.Developing reservoir tillage technology for semi-arid environments [J].Soil use and management，2007，23(2)：185-191.

[5] SALEM H M，VALERO C，MUOZ M，et al.Effect of integrated reservoir tillage for in-situ rainwater harvesting and other tillage practices on soil physical properties [J].Soil and tillage research，2015，151：50-60.

[6] SALEM H M，VALERO C，MUOZ M，et al.Short-term effects of four tillage practices on soil physical properties，soil water potential，and maize yield [J].Geoderma，2015，237/238：60-70.

[7] SALEM H M，VALERO C，MUOZ M，et al.Effect of reservoir tillage on rainwater harvesting and soil erosion control under a developed rainfall simulator[J].Catena，2014，113：353-362.

[8] 佟金 张智泓，陈东辉，等.凸齿镇压器与土壤相互作用的三维动态有限元分析[J].农业工程学报，2014，30(10)：48-58，293.

[9] 张智泓，佟金，陈东辉，等.不同材质仿生凸齿镇压器滚动件的模态分析[J].农业工程学报，2012，28(13)：8-15.

[10] KIM K U，SHIN B S.Modeling motion resistance of rigid wheels[J].Journal of Terramechanics，1985，22(4)：225-236.

[11] 高海波.用旋轮线方程求轮缘上点的速度和加速度[J].鄂州大学学报，1996(3)：36-37，46.

[12] WONG J Y.Behaviour of soil beneath rigid wheels [J].Journal of agricultural engineering research，1967，12(4)：257-269.

[13] NAKASHIMA H，KOBAYASHI T.Effects of gravity on rigid rover wheel sinkage and motion resistance assessed using two-dimensional discrete element method [J].Journal of terramechanics，2014，53：37-45.

Kinematics and Dynamics Analysis of Toothed Wheel Based on Finite Element Method

ZHANG Zhi-hong1, ZHANG Guang-kai1, TONG Jin2,3et al(1. School of Modern Agricultural Engineering, Kunming University of Science and Technology, Kunming, Yunnan 650500; 2. School of Biological and Agricultural Engineering, Jilin University, Changchun, Jilin 130025; 3. The Key Laboratory of Bionic Engineering, Jilin University, Changchun, Jilin 130025)

AbstractIn order to investigate the kinematics and dynamics characteristics of operating toothed wheel, we adopted the validated finite element model, solved the toothed wheel rim point motion trajectory, and obtained the change rule curves of velocity and acceleration velocity with the time. It was found that when toothed wheel rim point hit the soil, the speed at vertical direction did not reach its maximum; motion trajectory of toothed wheel rim point presented to be a fluctuating trochoidal curve. At the bottom of micro-basin, toothed wheel rim point motion had relative sliding in the opposite direction of movement.

Key wordsToothed wheel; Micro-topographical preparation; Finite element method; Motion trajectory solution; Kinematics and dynamics analysis

收稿日期2015-12-21

作者简介张智泓(1986- )，男，白族，云南昆明人，讲师，博士，从事农业机械化工程和农业工程仿生研究。

基金项目国家自然科学基金面上项目(51075185)；云南省科技计划项目青年项目(2015FD011)；云南省教育厅科学研究基金项目(2015Y079)；昆明理工大学引进人才科研启动基金项目(14118940)；昆明理工大学学生课外学术科技创新基金(2015BA132)。

中图分类号s 222.29

文献标识码A

文章编号0517-6611(2016)02-325-05