960 MPa高强度钢材轴压柱局部稳定性能及设计方法

2017-03-09徐克龙施刚林错错

湖南大学学报·自然科学版 2017年1期

关键词：设计

徐克龙+施刚+林错错

摘要：为研究960 MPa（屈服强度标准值）高强度钢材轴心受压构件的局部稳定受力性能，本文使用ANSYS软件建立有限元模型，对4个箱形截面和4个工字形截面轴心受压构件进行了有限元分析.模型考虑了几何初始缺陷及焊接残余应力的影响，提取构件的极限承载力和局部屈曲临界承载力的有限元计算结果与试验实测结果进行对比，验证了模型的有效性.利用这种建模方法，对960 MPa高强度钢材箱形和工字形轴心受压构件的局部稳定受力性能进行了有限元参数分析，并将有限元计算结果，以及本文汇总的已有试验结果，与中国、美国和欧洲的钢结构设计规范中轴心受压构件的设计曲线进行了对比，并提出了新的设计公式.结果表明，本文使用的有限元建模方法能够准确地分析计算960 MPa高强度钢材轴心受压构件的局部屈曲受力性能；几何初始缺陷和残余应力对构件的极限应力的影响很小，但是对板件宽厚比较大构件的局部屈曲应力的影响相对较大；相对于中美欧现行钢结构设计规范中的设计方法，本文提出的设计公式更适用于960 MPa高强度钢材轴心受压构件的局部屈曲应力和屈曲后极限应力的设计计算.

关键词：高强度钢材；轴心受压；局部稳定；有限元方法；设计

中图分类号：TU391 文献标志码：A

相对于普通强度钢材而言，960 MPa高强度钢材的应力应变曲线无明显的屈服平台并且材料的屈强比较大，并不满足大多数设计规范中对结构用钢材的材性要求，这限制了960 MPa高强度钢材在工程中的应用.而由于力学性能的变化，由此种钢材构成的焊接截面构件的受力性能将不同于普通强度钢材.此外，为了充分发挥高强度钢材强度高的优势，高强度钢材构件通常采用板件宽厚比较大的截面形式，这将导致构件的局部稳定性能成为重要的制约因素，钢构件由稳定性能控制而不是由强度性能控制的特性将更加显著[1-2].相关研究表明，对于高强度钢材受压构件，截面残余应力与钢材屈服强度的比值要比普通钢材构件小，从而能够提高受压构件的局部稳定承载力.此外，高强度钢材构件可以考虑利用板件局部屈曲后强度进行设计.

湖南大学学报（自然科学版）2017年

第1期徐克龙等：960 MPa高强度钢材轴压柱局部稳定性能及设计方法

目前，国内外对于960 MPa高强度钢材构件的局部稳定性能的研究较为有限，其中清华大学施刚等[3]对4个箱形截面构件和4个工字形截面构件进行了轴压试验研究.

本文运用通用有限元软件ANSYS，建立引入几何初始缺陷和残余应力的有限元模型，将计算结果与已有试验结果进行对比，验证有限元模型.随后利用此有限元模型，对960 MPa高强度钢材箱形截面和工形截面轴心受压构件的局部屈曲受力性能进行参数分析，将参数分析结果与中美欧的钢结构设计规范中相关计算公式进行对比分析，并提出新的设计计算方法.

1 有限元模型验证

1.1 有限元建模

本文选取文献[3]中960 MPa高强度钢材箱形截面和工字形截面短柱的轴心受压试验进行有限元模型的验证，采用通用有限元软件ANSYS进行分析计算，选取SHELL181单元和SOLID95单元建立有限元模型模拟轴心受压试验，建模计算过程与文献[4]和[5]所述类似.

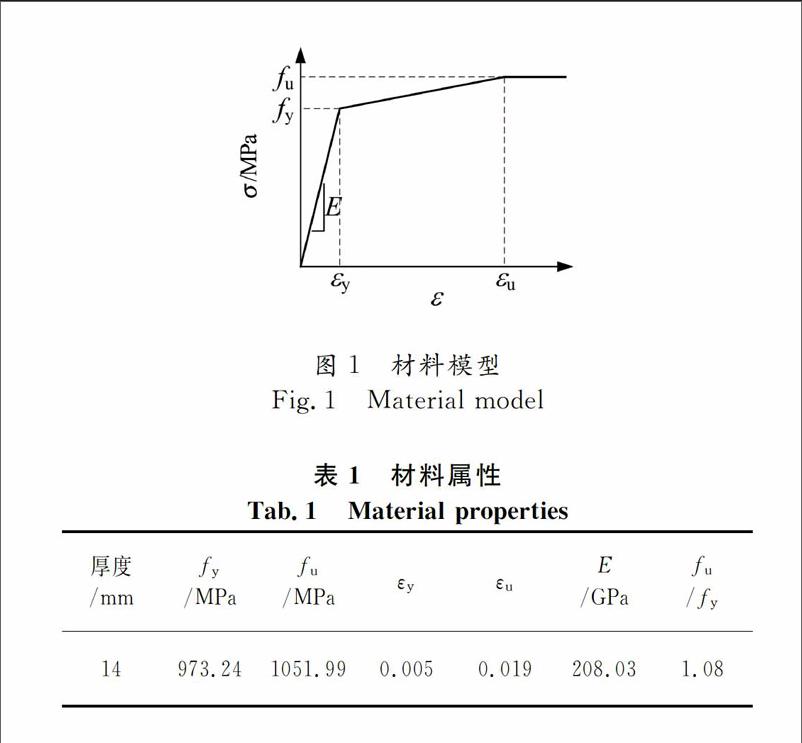
根据钢材力学性能试验结果[3]，所有试件的有限元模型均采用von Mises屈服准则，本构关系均采用三折线各向同性強化模型，如图1所示.试件的试验实测数据平均值如表1所示，其中，fy表示钢材屈服强度，fu表示极限强度，εy表示屈服应变，εst表示屈服平台末端应变，εu表示极限应变，E表示钢材弹性模量，ν表示泊松比.

湖南大学学报（自然科学版）2017年

第1期徐克龙等：960 MPa高强度钢材轴压柱局部稳定性能及设计方法

1 有限元模型验证

1.1 有限元建模

根据钢材力学性能试验结果[3]，所有试件的有限元模型均采用von Mises屈服准则，本构关系均采用三折线各向同性强化模型，如图1所示.试件的试验实测数据平均值如表1所示，其中，fy表示钢材屈服强度，fu表示极限强度，εy表示屈服应变，εst表示屈服平台末端应变，εu表示极限应变，E表示钢材弹性模量，ν表示泊松比.

图1 材料模型

Fig.1 Material model

表1 材料属性

Tab.1 Material properties

厚度

/mm

/MPa

εy

εu

/GPa

/fy

973.24

1051.99

0.005

0.019

208.03

1.08

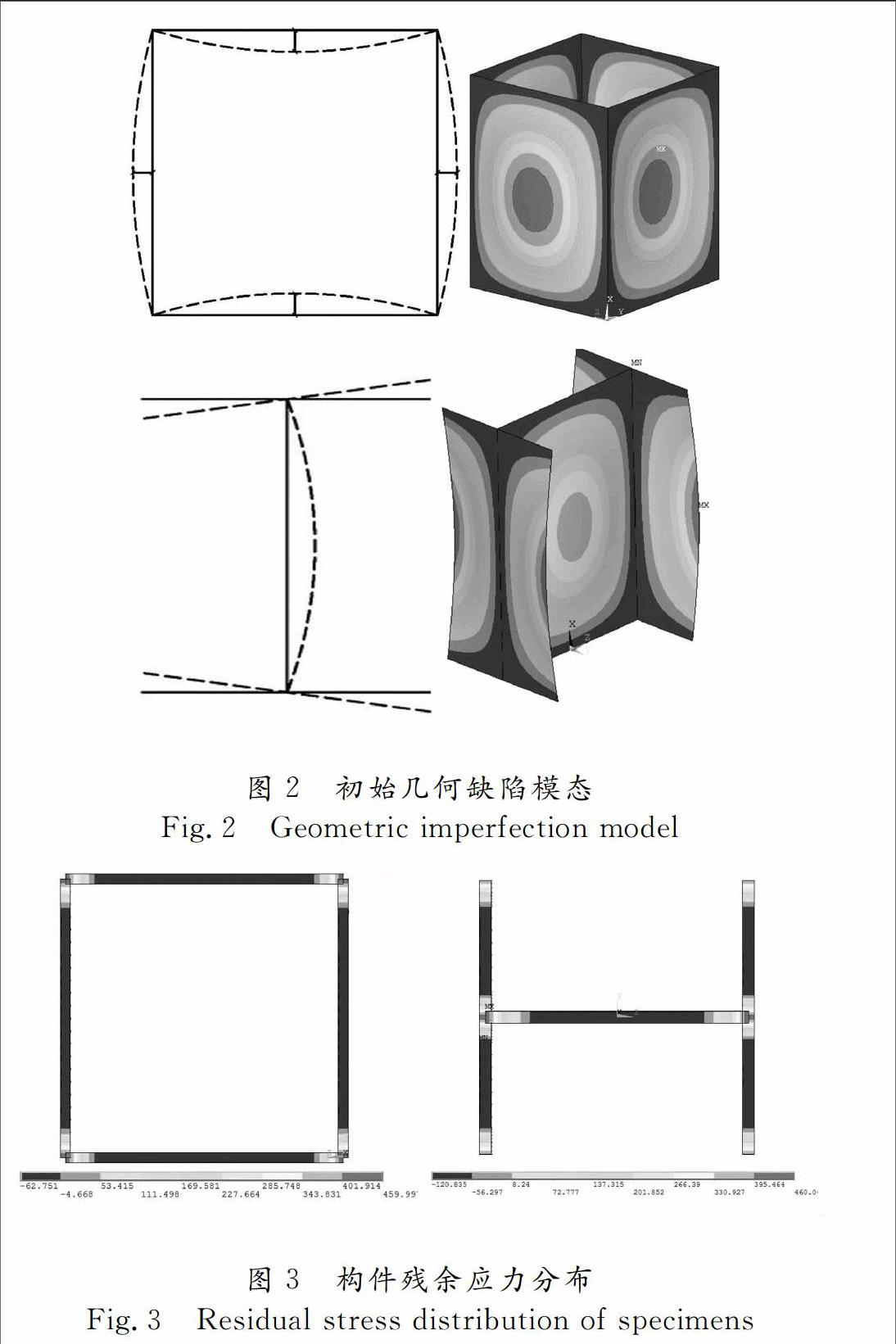
在进行钢构件的局部屈曲分析时，有限元模型一般以特征值屈曲分析中构件的第一阶局部屈曲模态作为构件的初始几何缺陷模态，如图2所示.缺陷模态的幅值采用文献[3]给出的所有试件的实测平均值.

图2 初始几何缺陷模态

Fig.2 Geometric imperfection model

本文分别根据文献[6]和[7]提出的残余应力分布模型和计算公式施加箱形截面和工字形截面试件的焊接残余应力，施加残余应力后试件的典型应力分布如图3所示.

图3 构件残余应力分布

Fig.3 Residual stress distribution of specimens

1.2 有限元结果与试验结果对比

本文对所建立的有限元模型的分析计算过程均分为四步，分别为静力求解、特征值屈曲分析、施加初始缺陷后非线性静力求解和提取计算结果.提取结果具体操作是分别提取时间步的最大值和构件鼓凸点中平面应变的最大压应变值对应的时间步，乘以所施加的轴压力，得到构件模型的极限承载力和局部屈曲承载力的有限元计算值，其中，根据“最大中平面应变法”[4]判定板件是否达到局部屈曲承载力.具体分析过程可参考文献[5]和[8].

两组试件极限承载力的有限元计算结果和试验结果的对比如表2所示.其中FT为试验值，FE为有限元计算值，Δ为（FE-FT）/FT.可见，本文所建立的有限元模型能够准确地分析计算960 MPa高强度钢材轴心受压构件的局部屈曲极限承载力.

标准差

3.99

可见，上述对比结果偏差的平均值及标准差均较小，验证了此有限元模型的准确性和可靠性，能够准确模拟960 MPa高强度钢材轴心受压构件的局部稳定受力性能.

2 参数分析

采用上述经过验证的建模方法，对960 MPa高强度钢材轴心受压构件的屈曲后极限承载力和局部屈曲承载力进行参数分析研究.由于工字形构件腹板与箱形构件板件的支承条件相似，轴心受压下其局部屈曲受力性能变化规律一般认为与箱形构件板件相同.因此，本文只研究板件宽厚比、局部几何初始缺陷幅值和残余压应力值对箱形截面构件板件和工字形截面构件翼缘的屈曲后极限应力和屈曲临界应力的影响.

箱形截面和工字形截面标准组构件的截面形式和构件尺寸分别如图4，表5和表6所示.根据实际工程经验，选定箱形构件钢板厚度为10 mm，工字形构件翼缘、腹板厚度分别为14 mm，10 mm；工字形构件腹板的宽厚比取为20，避免腹板发生局部屈曲而影响翼缘的局部屈曲；箱形構件钢板宽厚比范围为10～70，工字形构件翼缘宽厚比范围为5～35；

根据标准组构件计算结果可见：

1）随着板件宽厚比的增大，箱形构件板件和工字形构件翼缘的屈曲后极限应力和局部屈曲应力均随之减小.

2）对于箱形截面构件，当板件宽厚比小于30时并没有发生局部屈曲，局部屈曲承载力与极限承载力相同；当板件宽厚比大于30时，板件出现局部屈曲，且应力比（σcrb/σub）随宽厚比的增大而减小，这表明板件的屈曲后强度在提高.

3）对于腹板高厚比为20的工字形截面构件，当翼缘宽厚比大于5时，翼缘先于腹板发生局部屈曲，且应力比（σcrf/σuf）随宽厚比的增大而减小，这表明板件的屈曲后强度在提高.

2.2 工字形构件腹板对翼缘的约束作用

针对工字形构件翼缘，以腹板高厚比为研究参数，本文分别选取工字形构件腹板高厚比为20（标准组），40和60的三组构件，其他参数均相同，计算分析翼缘的局部屈曲受力性能.三组构件翼缘局部屈曲后极限应力的计算结果如表10所示.可以看出，翼缘极限应力随腹板高厚比的增大呈减小的趋势，并且在翼缘宽厚比较小时，腹板高厚比的影响较大，但偏差均小于20%.因此，工字形构件翼缘和腹板的屈曲后极限承载力可以分开独立计算.

三组构件翼缘局部屈曲应力的计算结果如表11所示，需要说明的是，本文仅关注先屈曲板件的局部屈曲临界应力.可以看出，随着腹板高厚比的增大，翼缘宽厚比较小的试件腹板先于翼缘发生局部屈曲，先屈曲的翼缘的局部屈曲应力均随着腹板高厚比增大而减少，且偏差较大.但为了简化设计方法，本文将偏于安全地以计算结果的下限值分别提出翼缘和腹板的局部屈曲应力的独立设计公式.

0/500，h0/200（标准组）和h0/50以及工字形构件翼缘局部几何初始缺陷幅值为bf/500，bf/200（标准组）和bf/25，其他参数均相同，进行对比分析.三组构件板件屈曲后极限应力的计算结果对比如表12所示.可以看出，局部几何初始缺陷幅值变化对于极限应力的影响不超过15%.因此，局部几何初始缺陷幅值的变化对于960 MPa轴心受压柱的极限承载力的影响很小.

三组构件板件局部屈曲应力计算结果对比如表13所示.可以看出，当缺陷幅值减小时，板件局部屈曲应力增大；当缺陷幅值增大时，板件局部屈曲应力减小.并且，对于部分板件宽厚比较大的构件，缺陷幅值对其屈曲应力的影响超过50%.因此，在960 MPa轴压受压构件的加工过程中，需要严格控制加工工艺以减小局部几何初始缺陷的不利影响.2.4 残余压应力值

以残余压应力值为研究参数，本文分别选取残余压应力值为标准组构件板件残余压应力值0.5倍和1.5倍的构件组与其进行比较，其他参数均相同.三组构件板件的局部屈曲后极限应力的计算结果对比如表14所示.可以看出，残余压应力的变化对于极限应力的影响不超过5%.因此，残余压应力的变化对于960 MPa轴心受压柱的局部屈曲后极限承载力的影响很小.

三组构件板件的局部屈曲应力计算结果对比如表15所示.可以看出，当残余压应力值减小时，板件局部屈曲应力增大；当残余压应力值增大时，板件局部屈曲应力减小.并且，对于部分板件宽厚比较大的构件，残余压应力值对其屈曲应力的影响超过20%.因此，在计算960 MPa轴压受压构件局部屈曲承载力时，需要考虑残余压应力的不利影响.

4 结论

利用有限元软件ANSYS建立模型，对960 MPa高强度钢材箱形和工字形轴心受压构件的局部屈曲受力性能进行了研究，并将参数分析结果与中国、美国和欧洲的钢结构设计规范的设计曲线进行了对比，并提出了960 MPa高强度钢材箱形和工字形轴心受压构件板件屈曲后极限应力和局部屈曲应力的建议计算公式.基于上述工作，本文结论如下：

1）建立的有限元模型考慮了几何初始缺陷和焊接残余应力的影响，能够较为准确地分析计算960 MPa高强度钢材轴心受压构件的局部稳定受力性能.

2）板件屈曲后极限应力和局部屈曲应力随宽厚比增加而减小；几何初始缺陷和残余应力对屈曲后极限应力影响较小，对局部屈曲应力影响较大.

3）提出的建议设计公式（11）和（12）能够较好地预测960 MPa高强度钢材轴心受压箱形构件板件和工字形构件翼缘和腹板的屈曲后极限应力.

4）提出的建议设计公式（16）能够较好地预测960 MPa高强度钢材轴心受压箱形构件板件和工字形构件腹板的局部屈曲应力；本文建议仍然采用中国规范的设计公式计算960 MPa高强度钢材轴心受压工字形构件翼缘的局部屈曲应力.

参考文献

[1] 施刚，王元清，石永久. 高强度钢材轴心受压构件的受力性能[J]. 建筑结构学报，2009，30（2）：92-97.

SHI Gang， WANG Yuanqing， SHI Yongjiu. Behavior of high strength steel columns under axial compression [J]. Journal of Building Structures， 2009， 30（2）： 92-97. （In Chinese）

[2] SHI Gang， HU Fangxin， SHI Yongjiu. Recent research advances of high strength steel structures and codification of design specification in China [J]. International Journal of Steel Structures， 2014， 14（4）： 873-887.

[3] 施刚，林错错，周文静，等. 960MPa高强度钢材轴心受压构件局部稳定试验研究[J]. 建筑结构学报，2014，35（1）：126-135.

SHI Gang， LIN Cuocuo， ZHOU Wenjing， et al. Experimental study on local buckling of 960 MPa high strength steel columns under axial compression [J]. Journal of Building Structures， 2014， 35（1）： 126-135. （In Chinese）

[4] TILLMAN S C， WILLIAMS A F. Buckling under compression of simple and multicell plate columns[J]. ThinWalled Structures， 1989， 8（2）： 147-161.

[5] 施刚，徐克龙，林错错. 460MPa高强度钢材工字形截面轴心受压柱局部稳定有限元分析和设计方法研究[J].工业建筑，2016，46（7）：22-31.

SHI Gang， XU Kelong， LIN Cuocuo. Finite element analysis and design method study on the local buckling of 460MPa high strength steel I-section columns under axial compression [J]. Industrial Construction， 2016，46（7）：22-31. （In Chinese）

[6] 班慧勇，施刚，石永久. 960MPa高强钢焊接箱形截面残余应力试验及统一分布模型研究[J]. 土木工程学报，2013，46（11）： 63-69.

BAN Huiyong， SHI Gang， SHI Yongjiu. Experimental study on residual stress in 960MPa high strength steel welded box sections and unified model [J]. China Civil Engineering Journal， 2013，46（11）： 63-69.（In Chinese）

[7] 班慧勇，施刚，石永久. 高强钢焊接构件工字形横截面残余应力试验及统一分布模型研究[J]. 工程力学，2014，31（8）：83-91.

BAN Huiyong， SHI Gang， SHI Yongjiu. Experimental and unified model investigations on residual stress within high strength steel welded I-sections [J]. Engineering Mechanics， 2014，31（8）：83-91.（In Chinese）

[8] 施刚，林错错，周文静，等. 460MPa高强钢箱形截面轴压柱局部稳定有限元分析和设计方法研究[J]. 工程力学，2014，31（5）：128-136.

SHI Gang， LIN Cuocuo， ZHOU Wenjing， et al. Finite element analysis and design method study on the local buckling of 460MPa HSS box section axial compressed columns[J]. Engineering Mechanics， 2014， 31（5）：128-136.（In Chinese）

[9] GB 50205—2001 鋼结构工程施工质量验收规范[S]. 北京：中国计划出版社，2001： 30-31.

GB 50205—2001 Code for acceptance of construction quality of steel structures [S]. Beijing： China Planning Press， 2001： 30-31. （In Chinese）

[10]林错错. 高强度钢材焊接截面轴压构件局部稳定性能和设计方法[D]. 北京：清华大学，2012： 60-79.

LIN Cuocuo. Local buckling and design method of high strength steel weldedsection members under axial compression [D]. Beijing： Tsinghua University， 2012： 60-79. （In Chinese）

[11]GB 50017—2003 钢结构设计规范[S] . 北京：中国计划出版社，2003.

GB 50017—2003 Code for design of steel structures [S]. Beijing： China Planning Press， 2003. （In Chinese）

[12]AISC 360-10 Specification for Structural Steel Buildings [S]. Chicago： American Institute of Steel Construction， 2010.

[13]EN 1993-1-5 Eurocode 3： Design of steel structuresPart 15： Plated structural elements [S]. Brussels： European Committee for Standardization， 2006.

[14]何保康. 轴心压杆局部稳定试验研究[J].西安冶金建筑学院学报，1985，41（1）： 20-34.

HE Baokang. Experimental study of local buckling of the centrally compressed members[J]. Journal of Xian Institute of Metallurgy and Construction Engineering， 1985， 41（1）： 20-34. （In Chinese）