轨道交通开行方案优化模型研究综述
2016-03-04张星臣
于 剑 张星臣 许 璐
(中国铁路经济规划研究院1) 北京 100038) (北京交通大学交通运输学院2) 北京 100044)
轨道交通开行方案优化模型研究综述
于剑1)张星臣2)许璐2)
(中国铁路经济规划研究院1)北京100038)(北京交通大学交通运输学院2)北京100044)
摘要:列车开行方案是轨道交通运输组织中的核心技术计划,亦是研究热点之一.文中总结了轨道交通列车开行方案典型优化模型和求解方法,分析了目前研究的不足.优化模型方面,归纳出运营商和旅客2类共14种优化目标,及车站能力约束、区间能力约束、车底运用约束、乘务规则约束、客流关联约束、服务水平约束、其他相关约束7类共24种约束条件;求解算法方面,归纳出常用的启发式算法和数学解析方法2类共13种方法,并指出了现有成果在客流分配和算例规模方面的不足.
关键词:铁路运输;研究综述;文献查阅;开行方案;优化模型;求解方法
于剑(1990- ):男,硕士生,主要研究领域为交通管理工程
0引言
列车开行方案是轨道交通列车运输组织计划的核心内容之一,一般包括5项内容,即交路计划(route/path planning),开行频率(frequency)、停站计划(halting pattern)、列车编组(fleet size)和列车类型(train mode).交路方案.决定列车开行的起讫点和经由路径;开行频率.决定某条交路单位时间内的开行对数,进而决定了其服务能力;停站方案.决定列车在其经由路径内的停站方法,对服务能力和服务质量有重要影响;编组计划.决定列车编组长度,同样对服务能力有决定性作用;列车类型.决定列车的速度等级、车型、席位席别等.
开行方案从根本上决定了轨道交通服务产品,问题本身又具有高复杂性,得到了国内外学者的广泛重视,相关文献数量较多.以往的研究综述如王爽等[1]、闫海峰等[2]、左大杰等[3],强调了分步求算、循环迭代的思想,但大都偏重于定性分析,为深入研究开行方案编制方法,有必要对其定量优化的主要手段——优化模型和求解方法进行系统总结.
1典型开行方案优化模型
大多数定量研究开行方案编制方法的文献都建立了优化模型.铁路和城市轨道交通虽然因为各自特性的不同,在模型内容和侧重点上有一定区别,如铁路可能将停站优化作为重点之一,客流分配也需要考虑列车等级甚至时刻表,而城轨可能将开行频率与客流波动的匹配作为优化重点,客流分配更加注重换乘路径比选等,但模型形式上是相似的,常见的种类有单目标模型(如蓝伯雄等[4])、多目标模型(如彭其渊等[5])、双层规划模型(如王永亮等[6])等,其中双层规划模型的上层一般用来评价、约束开行方案,下层一般用来进行客流分配,且大量文献认为客流分配符合用户平衡.这些模型虽各有侧重,但仍有较多相似性,现分为优化目标和约束条件2个部分对相关文献中的开行方案优化模型进行总结,其中客流分配是较为独立的步骤,作为一大研究方向有大量文献,此处不做综述,且各文献中重复的优化目标、约束未全做引用标号.
1.1优化目标
开行方案影响着运营商和旅客的效益,所以绝大多数模型的优化目标都同时考虑这2个方面(谭政红[7]认为,运营商成本应通过完善管理制度而不是牺牲旅客服务质量来控制,所以不考虑),具体包括:
1) 运营商方面运营商的效益包括收益和成本2个方面.
(1)运营商收益票价总额,即客票收入.史峰等[8]使用人公里票价率乘以旅客总周转量计算.
(2)运营商成本
•列车固定成本,即开行一列车的固定成本,主要是整备维修,员工工资福利等费用,如付慧伶等[9]、王媛媛等[10].
•列车运营成本,即列车在运营中的可变成本,包括折旧、能耗、材料购置等费用.文献[8]使用列车公里费用乘以列车走行距离计算,文献[11]将这项成本细化为列车公里总费用、车公里总费用、车小时总费用,2008年[11]增加列车组织费用.
•中转组织费用,文献[8]将其描述为一个关于中转人次数正相关的线性公式.
•列车开行时段数量,列车开行时段数量过多将增加运营成本,邓连波等[12-13]将最小化时段数量作为优化目标.
•区间断面客流量均衡度,文献[6]提出,指各区间上下行路段的断面客流量之比(以较小者作为分子)的平均值,反映城轨的正外部性.
•运能不足导致的客流流失惩罚成本,由蓝伯雄等[14]提出,用来体现轨道交通的公共服务特性,左大杰[15]极小化了剩余客流量.
•列车空位走行距离,此值越大代表列车坐席虚糜度越高,汪波等[16]将坐席虚糜度最小作为目标.
2) 旅客方面同理,旅客的效益也包括收益和成本2个方面.
(1)旅客收益文献[8]指出旅客在旅行中收益是位移,由于对于不同开行方案,旅客的位移并无差别,所以不将其纳入目标函数.文献[13]指出,考虑弹性旅客需求时,可将乘客人公里最大化作为优化目标.
(2)旅客成本
•票价支出,一般用客流量、人公里票价率、行程长度之积计算.
•乘车时间成本,即旅客在车上耗费的时间成本,可分为乘车运行时间成本和停站时间成本,杜欣等[17]将后者最小化作为目标,文献[10]给出了城轨大小交路下这两项的详细计算方法,文献[7]定义了始发集结时间.
•换乘时间成本,换乘时间是指旅客换乘过程的走行时间和等待时间之和(如文献[9-10]).有较多研究将最大化直达客流量作为优化目标,本质上是减少换乘时间成本.考虑换乘时间成本将使客流分配过程变得较为复杂,部分文献忽略了这部分成本,如Ralf Borndörfer等[18];部分研究将换乘时间成本设为定值,如王柄达等[19].
•旅行时间成本,是乘车时间成本与换乘时间成本之和.文献[11]将其表示为旅行时间、客流量和旅客平均时间价值三者的乘积.宋健等[20]和郑锂等[21]指出列车跨站开行有利的条件是长距离出行乘客得到的节约时间总和大于部分乘客增加的候车与换乘时间总和.
•中转风险,文献[8]提出,反映旅客除中转时间外所承担的风险和精神负担,取决于中转站往终点站的旅客运输能力,表示为换乘时间乘以一定参数.
•旅行舒适度,可用拥挤费用表示,文献[12]利用列车实际载客量和定员的比值定义(当实际载客量低于定员时,拥挤费用为0);类似的,文献[5]定义了旅客出行舒适度,与列车等级、速度、换乘时间、停站时间相关;由文献[8]提出的疲劳恢复时间,也用来反映乘车舒适度,与乘车环境和乘车时间相关;文献[20]定义的客专舒适度仅考虑列车和席位类型,不考虑载客量,陈胜波等[22-23]认为载客量与列车定员间的方差应最小化,满载率应在一定范围内;何宇强等[24]提出旅客方便性概念,由列车的发车时段决定.
1.2约束条件
开行方案约束条件保证了开行方案的可行性,数量较多,引用文献[16]对开行方案约束条件的分类方法,对相关文献中涉及到的约束条件总结如下(未列出个别不常见约束).
1) 车站能力约束
•车站接发车能力约束[25],类似的,部分文献考虑始发站发车能力约束、终到站终到能力约束[26]、车站通过能力约束
单位时间在车站通过或停靠的总列车数≤
车站接发车能力
(1)
•折返站折返能力约束
单位时间在车站折返的总列车数≤
车站折返能力
(2)
•中转换乘组织能力约束,类似的,有文献提出车站集散能力约束[27]
单位时间车站内中转换乘旅客的总人数≤
车站中转换乘组织能力
(3)
2) 区间能力约束区间最小追踪间隔约束[28],同理也可表示为区间最大通过能力约束,即区间开行频率小于能力允许的最大开行频率

(4)
3) 车底运用约束
•车底数量约束
∑每列车的编组长度≤可使用的车底总数
(5)
•各类列车的车辆小时总数约束,这是为了考虑运输资源的有限性,同理,也可表示为列车公里数约束
∑某类列车的车辆小时≤
该类列车的车辆小时总数最大值
(6)
•列车编组长度约束
最小编组长度≤列车编组长度≤最大编组长度
(7)
•列车检修约束,城市轨道交通系统一般不考虑这个约束
列车交路长度≤有关规定中列车的检修距离
(8)
4) 乘务规则约束乘务组不超劳约束,城市轨道交通系统一般不考虑这个约束
列车连续运行时间≤值乘该列车的
各乘务组最大值乘时间之和
(9)
5) 客流关联约束此类约束一般为对客流分配结果的约束,如OD间各客流路径上客流量的和(小于)等于该OD客流总量,列车最大车上人数小于等于列车满载人数等,本文不予详述.
6) 服务水平约束
•列车输送能力约束,此约束要求旅客运输需求量必须被全部满足,但考虑到实际中输送能力可能不足的情况,可不将此作为紧约束
∑区间上各列车定员×最大上座率≥
该区间断面客流量
(10)
•区间最大开行间隔约束,这是为了保证一定的服务质量

(11)
•最大、最小上座率约束[29],上座率的大小影响服务水平和运营成本
定员×频率×最小上座率≤区间断面客流量≤
定员×频率×最大上座率
(12)
•最低停站等级约束,减少停站可提高列车旅速
列车所停站等级≥该列车最低停靠站等级
(13)
•最小停站距离约束
相邻两停站间距离≥最小停站距离
(14)
•最大停站数量约束,高等级的高速铁路旅客列车应有一定的停站数量限制,以提高服务水平
某等级列车的停站数量≤
该等级列车最大停站数量
(15)
•必须停站要求约束,这是考虑到因技术作业或政治经济等因素要求列车必须在某些站停车的情况
必须停的站点集合⊆列车停站集合
(16)
•每站必须有列车停靠、每区间必须有列车经过约束[22,24]
停靠/通过各站、区间的列车数量≥1
(17)
•各时段内站站停列车至少开行1列[30]
•存在换乘可能的列车间必须有至少一个相同的停靠站
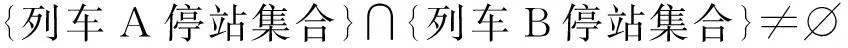
(18)
•停站数量对旅行速度的影响等式约束
列车速度系数=
(19)
•交路最大绕行率约束,交路长度与最短路径长度相比不应有太大差距,防止过远绕行,也有文献考虑交路最大长度约束
(20)
•最大、最小交路个数约束,这是考虑到经过各区段、始发终到站的不同交路数量不应过多的事实,文献[6]还考虑了全网最大、最小交路数.
最小交路个数≤区间、车站不同交路
数量≤最大交路个数
(21)
•网络最大旅客周转量约束、最大席位周转量约束、最小平均上座率约束(前两者的商)、最大平均旅客剩余率约束、最大平均换乘次数约束,对个别重点OD客流,单独考虑的剩余率、上座率约束
•直达率约束,这是一种最大化直达客流量的思想
(22)
7) 其他相关约束主要是各变量、符号的关系约束、非负约束、整数约束、0-1约束
2求解方法总结
在求解方法上,国内外形成了较鲜明的对比,中、大规模路网优化中,国内一般使用启发式算法求算满意解,而国外则偏向于使用数学方法寻求最优解,常用的规划求解软件是Cplex;对于小规模优化,国内文献一般使用Lingo软件求解.下面对现有文献中求解开行方案的启发式算法和数学方法进行总结.
2.1启发式算法
启发式算法在求算大规模问题时的优势是可在合理时间内得到满意解,所以应用较多,常见的开行方案启发式算法有:
1) 基于人工经验的算法文献[8]提出了基于编制人员“按流开车”经验的列车开行原则,设计了相应启发式算法,特点是只需计算一次,无迭代,效率高,可以用来生成初始方案和邻域方案.类似的还有文献[27]等.
2) 模拟退火算法模拟退火计划表是其核心,重点是设计解的邻域生成方法和退火规则.文献[11]利用模拟退火算法求解双层规划模型,客流分配运用了“GP配流算法”,使用类似方法的还有文献[12-13],其中文献[13]采用增广Lagrange算法进行客流分配,利用合并时段的方法降低开行时段数;再如周文梁等[31]利用模拟退火算法研究了开行方案和运行图的综合优化.
3) 禁忌搜索算法禁忌搜索算法通过引入禁忌表防止迂回搜索,同时通过藐视准则赦免被禁忌的优良解,是一种有效的全局搜索算法.文献[22]设计了禁忌表,采用最大迭代次数作为终止规则,并讨论了禁忌长度的合理取值.
4) 遗传算法遗传算法通过模拟生物进化过程择优,是近年来受到广泛关注的全局搜索算法,其关键是编码方法、杂交和变异算子设计.文献[16]设计了含停站序列、速度等级、定员、频率等的染色体编码方法,染色体较长.文献[5]利用遗传算法求解其多目标模型,将开行频率和客流分配方案作为染色体,对小型路网进行了研究.董守清等[32]对交路和停站编码,利用群体飘移产生初始种群,采用Baltzmann选择策略,并使用协同对称群体交叉遗传算子.文献[6]将模拟退火算法和遗传算法混合,将后者作为主引擎,前者作为邻域解生成和判定的步骤,求解其双层规划模型.陈路锋等[33]利用遗传算法搜索备选集,每代对优良抗体进行邻域搜索并更新备选集.
5) 混沌算法混沌优化是混沌应用研究领域的一个崭新方向,适用于局部搜索.何宇强等(2006)[24]利用混沌算法求解其双层规划模型,对0-1决策变量建立相应混沌变量并载波,得到了满意解.
6) 拉格朗日松弛算法拉格朗日松弛算法将模型中的难约束转化为目标函数,并通过权重进行调整与松动,可降低优化难度.文献[9]利用拉格朗日松弛算法将模型分为客流分配和开行方案确定两个子问题,每次拉格朗日松弛算法迭代中分别利用线性规划方法和其他启发算法求解子问题.
7) 蚁群算法蚁群算法,又称蚂蚁算法,模拟的是蚂蚁寻找食物的过程.文献[31]利用蚁群算法对单线停站方案进行优化,Saeed Asadi Bagloee[34]将其运用于备选交路集的择优过程.
2.2数学解析方法
数学解析方法可以求出问题的最优解,但计算复杂,计算量大,适用于中小规模开行方案优化问题.文献中常见的几类数学方法或手段如下:
1) 利用LINGO软件求解LINGO意为“交互式的线性和通用优化求解器”,由美国LINDO系统公司推出,内嵌各类优化算法,以下文献均使用LINGO求解 (文献[35]利用EXCEL求解).
马长青等[36]基于情景集思想优化小规模线路的停站和频率;文献[18]对指定交路下的列车开行频率建模优化;文献[10]建立混合整数非线性规划模型,通过理想点法将多目标转化为单目标,并分析了相关参数对最优解的影响;文献[24]利用多目标模型对单线路备选交路集择优;
2) 动态规划法动态规划通过把原问题分解为相对简单的子问题的方式求解复杂问题.陈强等[37]利用动态规划法优化跨线开行频率,文献[19]求算网络中有长度限制的最长路径.
3) 列生成算法列生成算法主要应用于求解变量数远大于约束数的大型模型,子问题为主问题提供优秀的基变量,主问题提供引导子问题的对偶信息,此方法也经常与启发式算法、分支定界法结合.文献[15,19]设计了结合启发式算法的列生成算法,分别用CPLEX9.1,CPLEX10.1求解,证明列生成算法能有效减少计算量,提高求解效率.
4) 分支定界法、分支切割法分支定界(Branch-and-Bount)法和分支切割(branch-and-cut)法都是有效的整数、混合整数规划求解算法,Goossens, J.-W.等[38]应用后者求解模型.
5) 模糊数学规划法模糊数学规划法可将多目标线性规划问题转化为单目标线性规划问题,Yu-Hern Chang等[39]使用了该方法.
3结 束 语
开行方案编制是运输组织计划编制的核心工作之一,国内外学者对相关问题做出了较多探索,取得了一定成果,但也存在一些问题,如部分研究建立了客流平衡分配模型,而其在轨道交通领域运用的科学性有待论证,再如大多数文献算例规模较小,所提出的方法对大规模网络的求算效率不明确.今后的研究应着重在模型实用性、算法高效性和客流处理科学性方面做出更深层次的探索.
参 考 文 献
[1]王爽,赵鹏.客运专线旅客列车开行方案研究综述[J].综合运输,2008(4):58-62.
[2]闫海峰,董守清,李群仁,等.客运专线列车开行方案优化思路综述[J].铁道运输与经济,2008,30(5):69-71,75.
[3]左大杰,王慈光,陈韬,等.铁路旅客列车开行方案问题的研究综述[J].铁道运输与经济,2010,32(1):35-39.
[4]蓝伯雄,吴李知.高速铁路客运网络列车开行方案优化模型[J].中国管理科学,2010,18(6):51-58.
[5]彭其渊,贾晓秋,关晓宇,等.随机稳定性配流规划的客运专线列车开行方案模型[J].西南交通大学学报,2011,46(1):143-147.
[6]王永亮,张星臣,徐彬,等.城市轨道交通网络化列车开行方案优化方法[J].中国铁道科学,2012,33(5):120-126.
[7]谭政红.基于旅客服务特性的客运专线旅客列车开行方案研究[D].成都:西南交通大学,2013.
[8]史峰,邓连波,黎新华,等.客运专线相关旅客列车开行方案研究[J].铁道学报,2004,26(2):16-20.
[9]付慧伶,聂磊,杨浩,等.基于备选集的高速铁路列车开行方案优化方法研究[J].铁道学报,2010,32(6):1-8.
[10]王媛媛,倪少权.城市轨道交通大小交路模式列车开行方案的优化[J].铁道学报,2013,35(7):1-8.
[11]史峰,周文梁,陈彦,等.基于弹性需求的旅客列车开行方案优化研究[J].铁道学报,2008,30(3):1-6.
[12]邓连波,曾强,高伟,等.基于弹性需求的城市轨道交通列车开行方案研究[J].铁道学报,2012,34(12):16-25.
[13]邓连波,曾强,高伟,等.城市轨道交通列车开行方案优化方法[J].中国科技论文在线,2010,5(10):767-772.
[14]蓝伯雄,吴李知.铁路客运网络列车开行方案优化模型的列生成算法[J].运筹与管理,2012,21(1):1-10.
[15]左大杰.铁路快速客运网络旅客列车开行方案优化研究[D].成都:西南交通大学,2010.
[16]汪波,杨浩,张志华,等.基于周期运行图的京津城际铁路列车开行方案研究[J].铁道学报,2007,29(2):8-13.
[17]杜欣,牛永涛,韩宝明,等.基于节点重要度的客运专线旅客列车开行方案[J].北京交通大学学报,2010,34(6):5-10.
[18]RALF B, MARTIN G, MARC E. A column-generation approach to line planning in public transport[J]. Transportation Science,2007,41(1):123-132.
[19]王柄达.客运专线旅客列车开行方案编制优化方法研究[D].成都:西南交通大学,2010.
[20]宋键,徐瑞华,缪和平,等.市域快速轨道交通线开行快慢车问题的研究[J].城市轨道交通研究,2006,9(12):23-27.
[21]郑锂,宋瑞,何世伟,等.城市轨道交通跨站停车方案优化模型及算法[J].铁道学报,2009,31(6):1-8.
[22]陈胜波,何世伟,何必胜,等.基于免疫克隆选择算法的市域快速轨道交通列车开行方案优化研究[J].石家庄铁道大学学报:自然科学版,2013,26(3):81-86.
[23]陈胜波,何世伟,何必胜,等.客流波动条件下城市轨道交通列车开行方案研究[J].城市轨道交通研究,2013,16(10):53-58.
[24]何宇强,张好智,毛保华,等.客运专线旅客列车开行方案的多目标双层规划模型[J].铁道学报,2006,28(5):6-10.
[25]邓连波,史峰,周文梁.旅客列车停站设置方案优化[J].中国铁道科学,2009,30(4):102-107.
[26]黄武国.客运专线旅客列车开行方案研究[D].成都:西南交通大学,2011.
[27]熊星.基于混合集合规划的高速铁路列车开行方案优化研究[D].北京:北京交通大学,2012.
[28]DENG Lianbo, ZENG Qiang, GAO Wei, et al. Optimization method for train plan of urban rail transit[J]. ICCTP 2011: Towards Sustainable Transportation Systems-Proceedings of the 11th International Conference of Chinese Transportation Professionals,2011:1189-1199.
[29]佟璐,聂磊,付慧伶,等.基于运输组织模式导向的旅客列车开行方案模型研究[J].大连交通大学学报,2011,32(3):26-31.
[30]房霄虹.城市轨道交通网络化运输组织协调理论及方法研究[D].北京:北京交通大学,2010.
[31]周文梁.客运专线网络列车开行方案与运行图综合优化模型及算法[D].长沙:中南大学,2010.
[32]董守清,闫海峰,李群仁.基于运行网络配流的客专列车开行方案遗传优化研究[J].中国铁道科学,2012,33(4):105-111.
[33]陈路锋,宋瑞,何世伟,等.基于双层规划模型的高速铁路列车开行方案优化研究[J].铁道运输与经济,2013,35(6):18-23.
[34]Saeed A B, Avishai A C. Transit-network design methodology for actual-size road networks[J]. Transportation Research Part B-Methodological,2011,45(10):1787-1804.
[35]杨晓.客运专线旅客列车开行方案研究[D].北京:北京交通大学,2008.
[36]马长青,徐健.基于情景集的鲁棒列车开行方案问题研究[J].物流技术,2011,30(9):135-137.
[37]陈强,何世伟,宋瑞,等.动态规划方法研究城市轨道交通网状线路跨线列车开行方案[J].城市轨道交通研究,2010,13(3):17-22.
[38]Goossens J W, van Hoesel S, Kroon L. A branch-and-cut approach for solving railway line-planning problems[J]. Transportation Science,2004,38(3):379-393.
[39]CHANGYuhern, YEH Chunghsing, SHEN Chingcheng. A multiobjective model for passenger train services planning: Application to Taiwan’s high-speed rail line[J]. Transportation Research Part B: Methodological,2000,34(2):91-106.
Review on the Optimization Models of
the Train Line Plan in Rail Transport
YU Jian1)ZHANG Xingchen2)XU Lu2)
(EconomicPlanningInstituteofChinaRailway,Beijing100038,China)1)
(SchoolofTrafficandTransportation,BeijingJiaotongUniversity,Beijing100044,China)2)
Abstract:Line planning is a key technical plan and a research hotspot in the organization of rail transport system. This paper presents a systematical summary of the typical optimization models and solving methods of the line planning problem (LPP) of rail transport system and the shortcomings in the current study based on a number of relevant literatures. The summary of the optimization models includes 14 different objectives, classified as 2 categories considering the operators and passengers respectively; and 24 different constrains, classified as 7 categories: station capacity constrain, section capacity constrain, rolling stock operation constrain, crew management constrain, passenger flow constrain, service constrain and other related constrains; whereas the summary of the solving methods includes 13 different common methods, classified as 2 categories: heuristic algorithm and mathematical analysis method. Passenger flow assignment and the scale of the cases in the literatures are considered as shortcomings of the current achievements.
Key words:railway transportation; research review; literature review; line plan; optimization model; solving method
收稿日期:2015-11-27
doi:10.3963/j.issn.2095-3844.2016.01.040
中图法分类号:U292.6
