一种新的多重权重复杂公交网络模型的研究*
2016-03-04沈文国安新磊
张 莉 沈文国 安新磊
(兰州工业学院基础学科部1) 兰州 730050) (兰州交通大学数理学院2) 兰州 730070)
一种新的多重权重复杂公交网络模型的研究*
张莉1)沈文国1)安新磊2)
(兰州工业学院基础学科部1)兰州730050)(兰州交通大学数理学院2)兰州730070)
摘要:以传统的加权复杂网络为基础,构造了一种新的多重权重复杂网络模型.通过网络拆分,按每条边上权重性质的不同,将其拆分为单权值的复杂网络,同时研究了这种复杂网络的全局同步.并以此为基础,以公交停靠站点为节点,建立了多重权重公交网络模型.在此网络的每条边上,赋予具有不同意义的属性作为权值.以每条边上不同的权值为研究对象,采用Lorenz混沌系统进行数值仿真,讨论整个公交网络的平衡性问题.
关键词:多重权复杂网络;网络拆分;复杂网络同步;公交网络;网络平衡
张莉(1982- ):女, 硕士,讲师,主要研究领域为非线性系统建模和非线性动力学
*国家自然科学基金项目(批准号:61164003、11561038)、兰州交通大学青年科学研究基金项目 (批准号:2014024) 资助
0引言
近年来,复杂动力网络吸引了许多相关领域研究人员的注意,这些研究主要集中在网络建模、网络动力学分析、计算,以及应用等方面.在网络动力学分析中,同步问题可以很好地探究节点间的动力学特性,因此,研究复杂网络意义下的同步具有积极的现实意义[1-2].过去10 a里人们还是主要侧重于理论研究[3-5],离真正的实际应用还有相当长的一段路要走,今后这方面的一个重点就是如何将己有的理论成果应用于实际的复杂网络系统为人类社会服务.
现实中许多网络都是加权网络,边权为复杂网络中节点之间的关系提供了更加方便的表达方式,而权重及其分布会对网络的性质和功能产生重要影响,所以加权网络已经成为复杂网络研究的一个重要领域.近几年来,加权网络的同步化也被广泛研究[6-8].对于加权复杂网络,目前大部分都是对单权的复杂网络进行研究,而对于多个权值的复杂网络的研究相对较少[9-10],文献[9]为了分析股票间的相关性,建立了双重加权网络模型,从成交量和回报两方面研究了中国股票市场煤电板块.文献[10]在一般网络的数据分布模型上增加了站点的处理能力,考虑通讯代价和处理能力不同的双权复杂网络中的数据分布优化问题.
随着复杂网络研究的日渐成熟,其理论在城市公交网络中的应用越来越广泛.城市公交网络系统是一个复杂的、动态的、巨系统,目前很多复杂公交网络[11-13]的研究主要集中在一些网络的性质上,如平均最短距离、聚类系数、度分布和网络直径等,鲜有文章对公交网络的稳定性进行研究.
基于上述的讨论,文中研究了一种新的多重权重复杂网络模型,根据网络拆分的思想将其拆分为多个单权的复杂网络并研究了其全局同步问题.在此基础上,以公交站点为节点,建立多重权重公交网络模型,并从发车频次、客流密度和可达性等三个方面讨论了整个公交线网的稳定性,最后通过Lorenz混沌系统进行数值仿真.从结论可得知:(1)适当地增加发车频次,以及公交公共站点时,可以使公交网络更快地达到平衡,从而节约乘客的出行时间.(2)优化公交线路,当乘客出行较长距离时,使乘客的换乘次数最少,从而使出行最舒适.
1多重权复杂网络模型
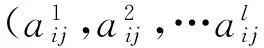
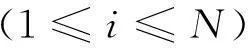
(1)
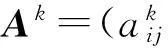
(2)
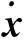
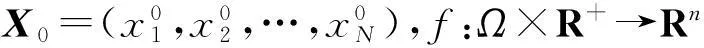
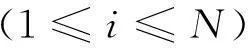
式中:x0⊆Ω.由此可知,式(1)所描述的系统就达到同步,并且Λ×…×Λ被称为动态网络系统的同步域.
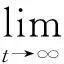
(3)
式中:F(xi,s,t)=f(x,t)-f(s,t)
h1(ej(t))=H1(xj(t))-H1(s(t))
h2(ej(t))=H2(xj(t))-H2(s(t))
⋮
hl(ej(t))=Hl(xj(t))-Hl(s(t))
下面给出定理中所需的假设与引理.
假设1假设存在非负常数α,满足∀t∈R+,有
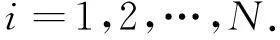
假设2假设存在非负常数βl,满足t∈R+,有
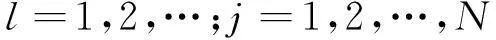
假设3假设多重权复杂网络中每条边的所有权重均非负.
引理1∀x,y∈R+,有2XTY≤XTX+YTY.
2同步准则
定理1若假设1和假设2成立,选取控制器为
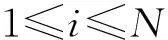
(4)
式中:d是正常数.
证明考虑如下的于Lyapunov函数
(5)
对V进行求导,并将式(3)和式(4)代入得
(6)
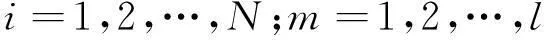
由假设1可得
于是
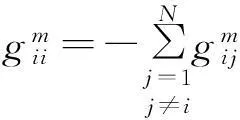
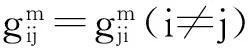
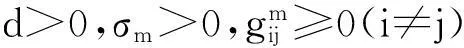
于是系统式(1)在式(4)的作用下趋于同步.
3多重权重公交网络模型
对于多重权重复杂网络每条边上的多个权值,文中有如下定义.
1) 发车频次公交线路上公交车发车间隔的时间.
2) 客流密度在公交线路的某个站点上,需要乘坐公交车的人数.
3) 可达性反映了某2个站点之间的连通情况.其大小定义为2站点之间直达公交车的车辆数的倒数.若无直达车,则为换乘2次可到达目的地的公交车辆数的倒数乘以2,若无换乘2次可达目的地的,则为换乘3次可到达目的地的公交车辆数的倒数乘以3.
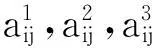

图1 三重权重复杂网络的拓扑结构图及拆分示意图
4数值仿真
高自友等在文献[14]中得到城市公交乘客流量满足非线性性质.通过对整个公交网络的研究分析可得整个公交线路网络模型具有BA无标度网络的特性.假设公交线路客流量变化量满足非线性Lorenz系统,即选取Lorenz混沌系统为网络节点的动力学方程,假设H1=H2=H3=diag(1,1,1),由式(1)得:当i=1,2,3,4时
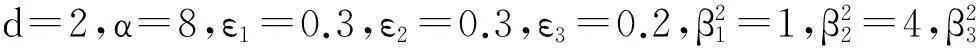
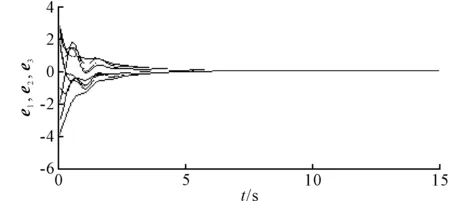
图2 复杂网络的误差收敛曲线
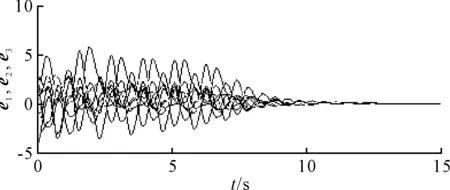
图3 复杂网络的误差收敛曲线
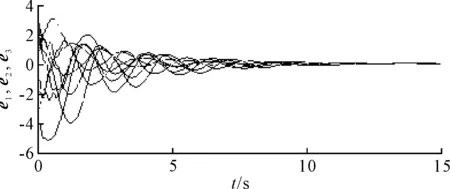
图4 复杂网络的误差收敛曲线
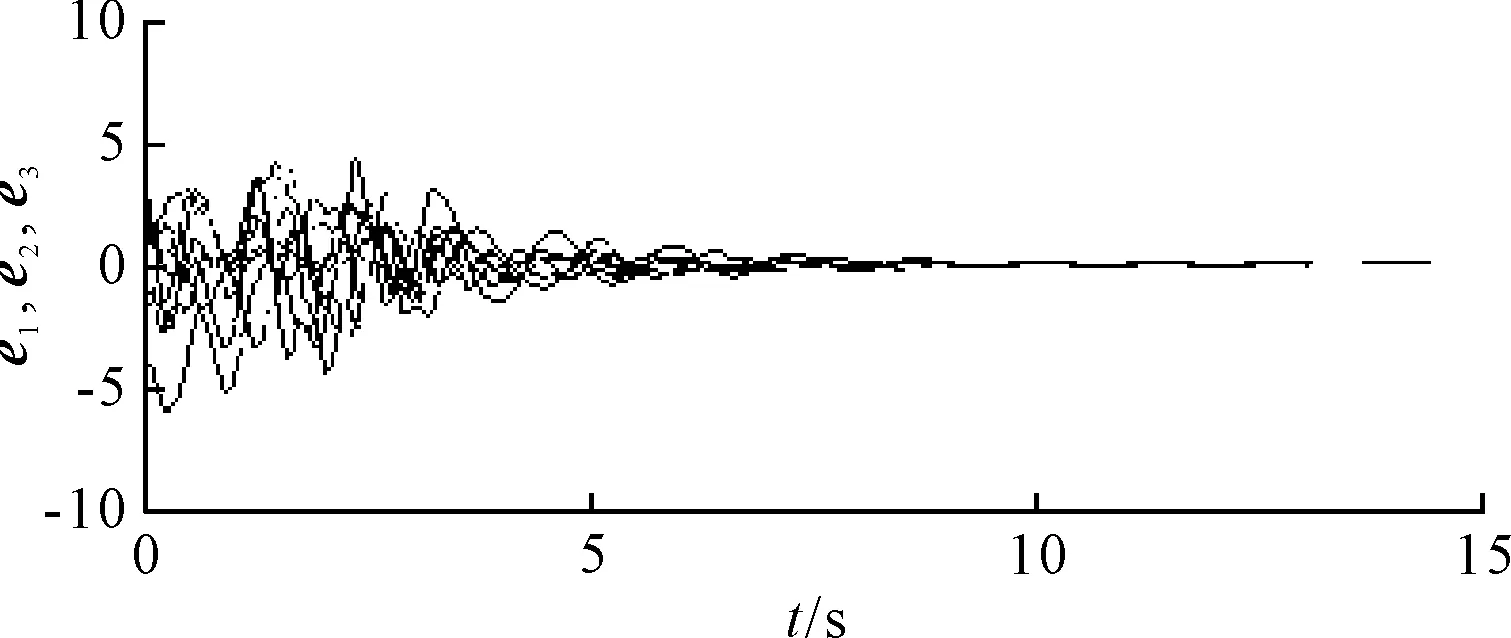
图5 复杂网络的误差收敛曲线
5结 束 语
文中在传统的单权重复杂网络的基础上,建立了一种新的多重权重复杂网络模型,并研究了其全局同步问题.在现实生活中,有很多问题都可以用多重权复杂网络来描述,例如有多重关系的不同公交线路组成的公交网络模型,有多种不同关系的人际关系网络等.文中把多重权重的思想引入公交网络,以发车频次、客流密度和可达性系数等公交系统中的3个指标作为多重权重复杂公交网络3个不同性质的权重,构建了多重权重公交网络模型.分别从上述3个指标讨论了此公交网络模型的平衡性问题.从结论中可以看出:适当地增加发车频次,可以使整个公交网络更快地达到平衡,减少乘客的出行时间;适当地对公交线路和公交站点进行优化,使乘客在出行较长距离时,尽量避免换乘或减少换乘次数,以便乘客出行最舒适.
参 考 文 献
[1]王瑞兵.复杂网络的同步及其在保密通信中的应用[D].镇江:江苏大学,2010.
[2]蒋强.复杂网络同步控制及其在电力系统中的应用研究[D].成都:西南交通大学,2011.
[3]LU J H, CHEN G R. A time-varying complex dynamical network model and its controlled synchronization criteria[J]. IEEE Trans. Automat, Control,2005,50(6):841-846.
[4]吕金虎.复杂动力网络的数学模型与同步准则[J].系统工程理论与实践,2004,24(4):17-22.
[5]CHEN G R, ZHOU J, LIU Z R. Global synchronization of coupled delay neural networks and applications to chaotic CNN models [J]. Int. J. Bifurcation and Chaos,2004,14(7):2229-2240.
[6]ZHANG R, HU M F, XU Z Y.Synchronization in complex networks with adaptive coupling [J]. Physics Letters A,2007,368:276-280.
[7]WANG Q Y, DUAN Z S, CHEN G R. Synchronization in a class of weighted complex networks with coupling delays[J]. Physica A,2008,387:5616-5622.
[8]郑海青,井元伟,刘晓平.一类时滞加权动态复杂网络的牵制同步[J].东北大学学报,2010,31(8):1065-1069.
[9]兰旺森,赵国浩.基于双重加权网络的股票强相关性分析[J].数学的实践与认识,2011,41(13):46-51.
[10]吴润秀,孙辉.双权复杂网络数据分布优化策略[J].南昌水专学报,2003,22(2):9-13.
[11]王波,王万良,杨旭华.一种基于加权复杂网络的最优公交换乘算法[J].武汉理工大学学报,2008,32(6):1113-1116.
[12]胡一竑.基于复杂网络的交通网络复杂性研究[D].上海:复旦大学,2008.
[13]王喆,彭其渊.成都市公交复杂网络拓扑特性研究[J].交通与计算机,2007,25(2):39-42.
[14]吴建军,高自友,孙会君,等.城市交通系统复杂性-复杂网络方法及其应用[M].北京:科学出版社,2010.
Study of a New Complex Public
Traffic Network Model with Multi-weights
ZHANG Li1)SHEN Wenguo1)AN Xinlei2)
(TheBasicCoursesDepartmentofLanzhouInstituteofTechnology,Lanzhou730050,China)1)
(SchoolofMathematicsandPhysics,LanzhouJiaotongUniversity,Lanzhou730070,China)2)
Abstract:Based on the traditional weighting network, this paper proposes a new multi-weights complex network model. According to the method of network split, splits the multi-weights complex network into several different single weighted complex networks, and studies its global synchronization. Using it as a base, taking bus stops as the network nodes, this paper establishes a new public traffic network model with multiple weights, and gives different properties weights in every edge. Regard the different weights as research object, taking the Lorenz chaotic system for example, discusses the balance of the whole public traffic roads network.
Key words:multi-weights complex network; network split; complex network synchronization; public traffic network; network balance
收稿日期:2015-11-05
doi:10.3963/j.issn.2095-3844.2016.01.022
中图法分类号:U121
