基于改进蚁群算法在软件缺陷预测中的应用
2016-03-03杨泽辉乔冰琴
杨泽辉,李 琳,乔冰琴
(太原理工大学财经学院经济信息系,太原 030024)
基于改进蚁群算法在软件缺陷预测中的应用
杨泽辉,李琳,乔冰琴
(太原理工大学财经学院经济信息系,太原 030024)
摘要:为提高软件缺陷预测算法的分类准确度和运算效率,将改进的蚁群算法应用于基于支持向量机的软件缺陷预测模型中。支持向量机作为二值分类模型进行软件缺陷预测,并对蚁群算法进行改进优化,每只蚂蚁只根据搜索半径参数在前次迭代中的最优解附近搜索,在缩小搜索范围的同时尽快实现最优解,并对支持向量机的参数进行优化。实验结果表明,与传统方法相比,该方法具有更高的预测精度和运算效率。
关键词:改进的蚁群算法;支持向量机;软件缺陷预测;运算效率
自20世纪70年代至今,软件缺陷预测技术一直伴随着软件工程飞速发展,该技术根据软件的复杂度、过程、规模等基本因素和软件历史数据来预测软件中隐藏但暂时未发现的缺陷[1],是软件评测过程中的关键过程,对提高软件可靠性、降低软件开发维护成本和缩短研发时间具有直接的促进作用。随着软件预测技术的发展,研究者统计发现在软件中缺陷并不是完全随机分布或者平均分布,研究得出软件工程学科内著名的“8/2原则”:80%的软件缺陷集中在20%的特定软件模块中,正是这部分易出错的软件模块造成软件发生错误[2],因此软件预测方法不用逐一审查出错软件的所有模块,在研发的初期集中资源预测有可能发生错误的模块,达到优化资源配置的目的,基于支持向量机的软件预测方法是其中一种应用较多的缺陷预测方法,将缺陷预测作为二值分类问题处理[3],综合统计学的VC维理论和结构风险最小原理在软件模型的学习能力和复杂度之间得到平衡,以得到较好的泛化能力。本文为了提高预测模型的准确性和效率,将一种改进的蚁群算法应用到基于支持向量机的软件缺陷预测模型中。
1改进的支持向量机算法
1.1 支持向量机
在分类问题方面,支持向量机[4]的基本原理是将初始的输入空间进行非线性变换,该变换以定义合适的内积函数φ(•)达成,输出的是一个高维空间,最优分类面从这个高维空间内得到。设样本集是(xi,yi),i=1,2,…M,M是样本集中样本数目,yi∈{+1,-1}是样本的类别,xi∈Rd是样本特性,得到的最优分类面如式(1)所示。
f(x)=ω•φ(x)+b=0
(1)
式(1)中,ω是权值矢量,b是阈值,分类面需满足式(2)所示的约束:
yi•(ω•φ(x)+b)≥1
(2)
以达到最小化结构风险的目的。
由于一些特定范围中的分类误差是不可避免的,因此需要引入非负松弛量ξi,所以可以表述数据分离面的优化问题如式(3)所示。
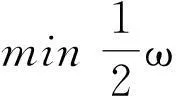
(3)
式中C是惩罚函数,用来控制错误样本的惩罚程度,同时还要满足式(4)的条件。
yi•(ω•φ(x)+b)≥1-ξi,ξi≥0
(4)
式中i=1,2,…m.
引入拉格朗日乘子算法,通过拉格朗日对偶原理简化求得二次规划问题,则式(3)可变为:
(5)
式中k(xi,xj)=φ(xi)•φ(xj)是核函数,且还需满足式(6)的条件:
(6)
而ai>0对应的点即支持向量,在此基础上得到的最优分类面如式(7)所示:
(7)
1.2 改进的蚁群算法
蚂蚁觅食时会沿途释放信息素,路径信息量越大蚂蚁更可能走,从而释放更多的信息素,这样造成一个良性循环,蚁群算法[5]是模拟蚁群觅食行为方式的优化算法,但蚁群算法易陷入局部的极值点。本文的改进算法设定蚂蚁以任意转向的方式搜索其可行空间内的最优解,在结束每次迭代时,全局最优解附近只有一只蚂蚁,同时在上次迭代结束时的最优解附近搜索全局最优解,这样可以缩小可行搜索空间的范围,提高搜索效率。
改进的蚁群算法主要分为三个流程:(1)初始化,(2)信息素更新,(3)求得最优解,算法流程图如图1所示。
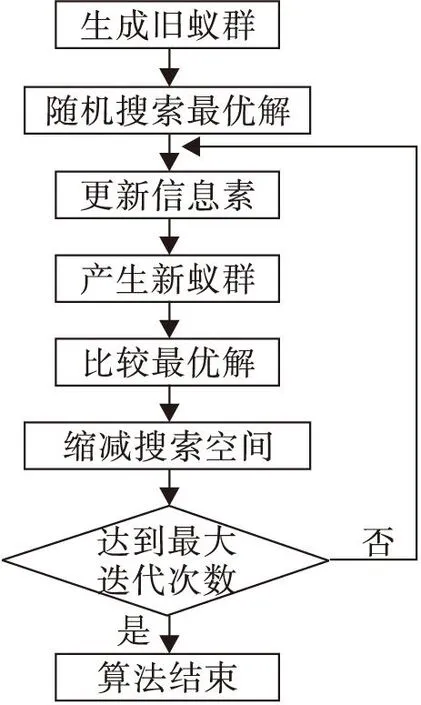
图1 改进蚁群算法流程
在第(1)阶段,生成一个旧蚁群,蚁群中的全部n只蚂蚁在可行搜索空间范围内随机搜索最优解,得到n个随机初始向量(xi,i=1,2,…n).然后进行第(2)阶段,更新信息素。在第(3)阶段,将蚁群蚂蚁按式(8)更新。
(8)
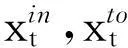
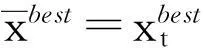
(9)
(10)
信息素在最优值区域变强,重复这个过程直到达到最大迭代次数为止。
1.3 优化的支持向量机算法
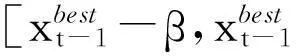
(11)
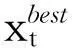
αt=0.99αt-1,βt=βt-1
(12)
重复迭代直到达到最大迭代次数为止,得出支持向量机C和σ的最佳参数,再运行支持向量机算法,得到最佳分类面。
2改进的软件缺陷预测模型
2.1 软件缺陷预测原理
软件的缺陷预测实质上是进行模式识别[7],分类问题是软件缺陷预测模型的基本要素。从组成上来说,一个软件是由许多编程模块按照一定的逻辑架构组合而成的,而模块的复杂度特性是用于表述模块内部的构设特征属性,这样模块的复杂度量属性和模块内部存在的缺陷个数可以映射出某种关联关系。利用支持向量机算法,对某些比较可能出错的软件模块的特征参数进行训练,并和对应模块的错误概率相关联,构造一个预测出错的黑箱模型。以这个黑箱模型为介质,来预测软件各模块的错误概率,从而实现软件缺陷预测。
2.2 软件缺陷预测模型的建立
运用改进的蚁群算法优化支持向量机的软件缺陷预测模型的流程图如图2所示。
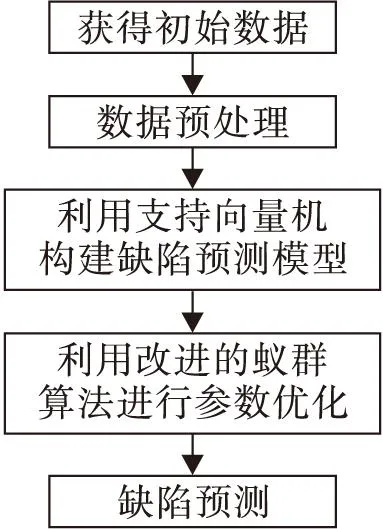
图2 改进的缺陷预测模型流程
首先需要获得表征软件复杂度特征的数据集,并进行简单的数据预处理,将冗余无用数据去除,避免浪费系统资源,将预处理后的数据做为样本,并以向量机为核心,建立构件缺陷预测模型,在模型中,以改进的蚁群算法对支持向量机进行优化,得出支持向量机的最佳参数,并以最佳参数条件下的支持向量机进行缺陷预测。
2.3 实验及结果
为了对改进后的算法进行验证,利用MATLAB 2007软件进行编程测试,实验数据来自NASA的NASA IV&V Facility Metrics Data Program(MDP)数据集[8]。
虽然MDP数据集已广泛应用,但很少有人研究其中有可能存在的问题,最新研究成果表明,这些MDP数据集中存在一定的矛盾数据、重复数据,会对软件缺陷预测的实验结果造成影响。因此首先进行数据预处理,将这些重复或者矛盾的数据删除。选取MDP中的JM1数据集作为实验数据,并进行预处理,两个数据集的信息如表1所示。
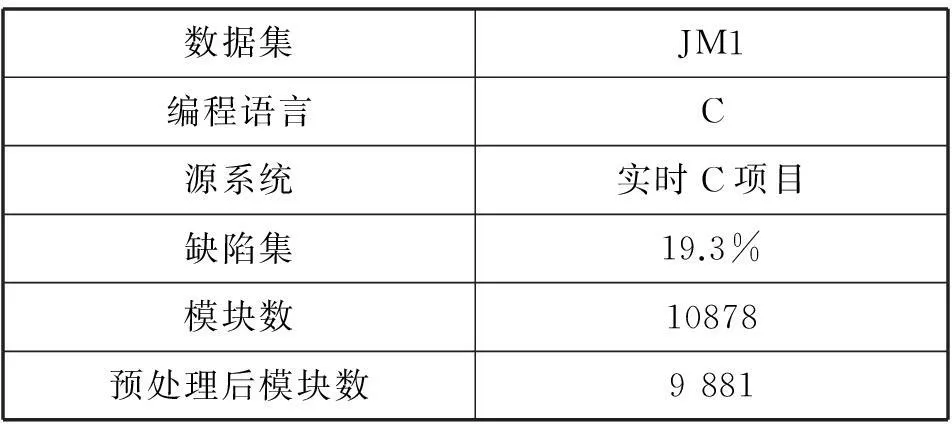
表1 实验数据
对这个数据集,采用数据挖掘领域公认的十折交叉验证方法[9],将数据集均分为10份,各份数据不交叉,在各次试验中,轮流取其中9份数据集用于训练,另外一份用于测试,重复10次,最后的分类测试结果取平均值。
为了测试改进算法的效能,同时进行标准蚁群算法支持向量机的缺陷预测软件的性能测试,两个模型除蚁群算法不同之外,其余条件相同,两种算法对JM1数据集得出的最优参数如表2所示。

表2 最优参数实验数据比较
在评价体系里,将所有模块分为正确模块和缺陷模块两类,按预测结果分为四类,如表3所示。
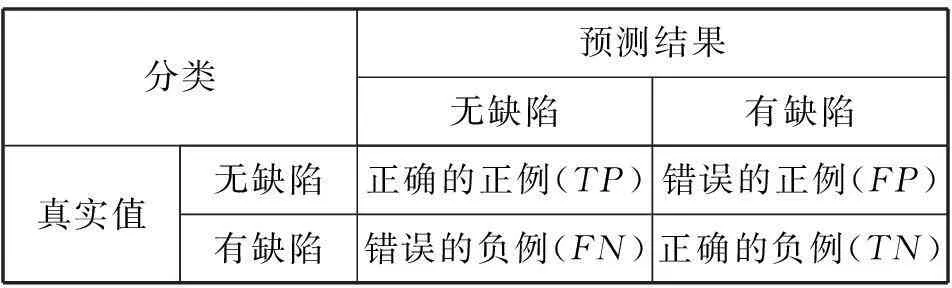
表3 分类比较
设模块总数目为N=TP+FP+FN+TN,以模糊矩阵为基础,设置准确率、查准率、查全率和F1值[10]作为缺陷预测模型的预测能力的定量性能分析标准。准确率Pa是模块有无缺陷预测的结果与实际情况一致的模块数目占总的模块数目的比例,其计算公式如式(13)所示:
(12)
查准率Pp是预测结果有缺陷实际也有缺陷的模块所占比例,计算公式如式(13)所示:
(13)
查全率Pr是指正确预测的缺陷模块的比例,计算方法如式(14)所示:
(14)
F1值是准确率和查全率的调和平均值,其计算方法如式(15)所示:
(15)
运用MATLAB编程进行运算,比较标准算法和改进算法的准确率、查准率、查全率和F1值,得到的柱形图如图3所示。
由图3可以看出,相比基于蚁群算法支持向量机的缺陷预测模型,通过改进的蚁群算法,缺陷预测模型的准确率、查准率、查全率和F1值都有一定的提高,证明改进算法在性能上得到提升。同时利用MATLAB中的etime函数测得程序的运行时间如表4所示。
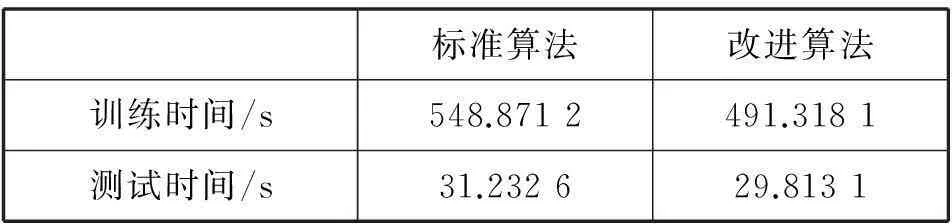
表4 运行时间比较
从表4可以看出,算法改进后,训练时间由548 s变为491 s,训练时间缩短为原来的89.5%,效果较为明显,测试时间由31.232 6 s缩短为29.813 1 s.
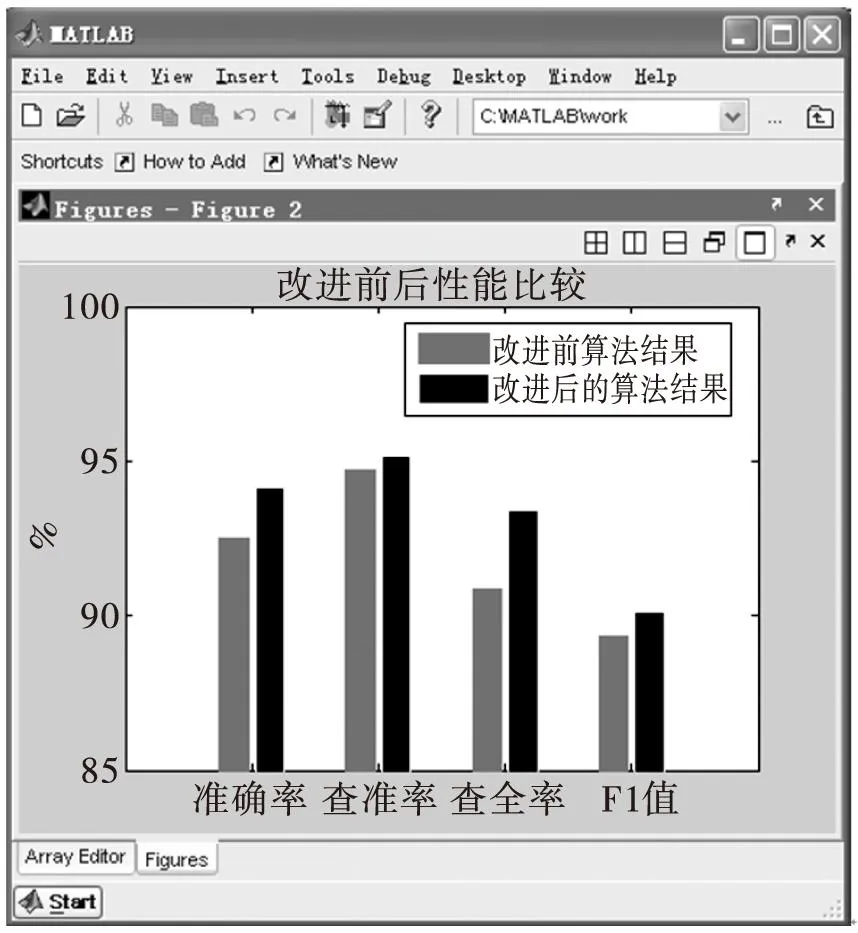
图3 算法结果
3结论
在基于支持向量机的软件缺陷预测模型的基础上,对支持向量机的蚁群算法进行优化改进,使每只蚂蚁只根据设定的搜索半径在前次迭代中的最优解附近搜索,在缩小搜索范围的同时尽快实现最优解,提高运算效率。实验结果表明,优化后的算法与原算法相比,训练时间、测试时间变短,准确率、查全率、查准率、F1值也得到提升,测试能力得到优化。但该算法需要较大的样本数目时才能取得较明显的效果,此外搜索半径的选取算法评估还需要进一步明确,在保证搜索效率的同时尽量提高模块预测性能。
参考文献:
[1]雷挺.基于缺陷分类和缺陷预测的软件缺陷预防[J].计算机工程与设计,2013,34(1):215-220.
[2]包祎.应用直线集合分割的软件缺陷预测模型[J].计算机工程与应用,2013,49(14):34-38.
[3]LOU DER-CHYUAN,LIU CHIANG-LUNG,LIN CHIN-LIN.Message estimation for universal steganalysis using multi-classification support vector machine[J].Computer Standards & Interfaces,2009,31(2):420-427.
[4]王培,金聪.遗传优化支持向量机在软件缺陷预测中的应用[J].电子测量技术,2012,35(2):126-129.
[5]袁东锋,吕聪颖.改进蚁群算法在二次分配问题中的应用[J].计算机与现代化,2013,39(3):9-16.
[6]王涛,李伟华,刘尊,史豪斌.基于支持向量机的软件缺陷预测模型[J].西北工业大学学报,2011,29(6):864-870.
[7]李倩茹,姚伟.基于均衡有偏支持向量机的软件缺陷预测[J].计算机工程,2013,39(8):87-91.
[8]JIANG YUAN,LI MING,ZHOU ZHI-HUA.Software defect detection with ROCUS[J].Journal of Computer Science and Technology,2011,26(2):328-342.
[9]吴晓萍,赵学靖,乔辉等.基于LASSO-SVM的软件缺陷预测模型研究[J].计算机应用研究,2013,30(9):2748-2754.
[10]姜慧研,宗茂,刘相莹.基于ACO-SVM的软件缺陷预测模型的研究[J].计算机学报,2011,34(6):1148-1154.
Application of Improved Ant Colony Algorithm in Software Defect Prediction Model
YANG Ze-hui,LI Lin,QIAO Bing-qin
(Institute of Finance and Economics,Taiyuan University of Technology,Taiyuan 030024,China)
Abstract:For raising the classified accuracy and the operational efficiency of the software defect prediction algorithm,the improved ant colony algorithm is used in the software defect prediction model based on support vector machine.The support vector machine algorithm operates as binary classifying model to realize the software defect prediction.The ant colony algorithm is improved and optimized,in which each ant searches near the optimum solution of the last iteration according to the parameter of searching radius.The final optimum solution can be acquired as soon as possible while the searching band is reduced,and the parameters of the support vector machine are optimized.The experimental results prove that the improved algorithm has higher prediction accuracy and operational efficiency by comparing with the traditional algorithm.
Key words:software defect (DP)prediction,improved ant colony algorithm(ACA),support vector machine(SVM),operational efficiency
中图分类号:TP311.5
文献标志码:A
doi:10.3969/j.issn.1673-2057.2016.01.004
文章编号:1673-2057(2016)01-0017-05
作者简介:杨泽辉(1979-),男,讲师,主要研究方向为无线通信技术和软件工程软件测试技术。
基金项目:山西省科技攻关项目(20130321002-05)
收稿日期:2014-11-21
