塔式起重机的分数阶滑模定位和防摆控制
2016-03-03陈志梅张井岗邵雪卷
陈志梅,孙 辉,张井岗,邵雪卷
(太原科技大学电子信息工程学院,太原 030024)
塔式起重机的分数阶滑模定位和防摆控制
陈志梅,孙辉,张井岗,邵雪卷
(太原科技大学电子信息工程学院,太原 030024)
摘要:针对塔式起重机防摆控制系统,考虑塔机的回转运动和变幅运动,提出了分层分数阶滑模定位和防摆控制新方法。把塔式起重机防摆控制系统分为小车位移控制系统和负载摆角控制系统两个子系统,采用两层分数阶滑模面,分别设计分数阶滑模控制器控制臂架小车的位移、起重臂的回转角及负载的摆角。与传统的整数阶滑模控制方法相比,加快了系统的响应速度,增强了系统的鲁棒性,改善了系统的控制性能,有效保证臂架小车精确定位和负载的消摆。仿真结果也表明分数阶滑模控制是提高此系统控制性能的一种更有效的方法。
关键词:塔式起重机;回转;变幅;分数阶;分层滑模控制
塔式起重机在工作过程中,由于其频繁的启动、制动以及受各种外界因素的干扰(如风力、摩擦力、力矩转动等),使得起重机所吊重物来回摆动。由于摆振的存在,对塔身产生周期性的倾矩和扭矩,导致系统定位精度降低,辅助工作时间延长,效率降低,同时也增加了操作工人的劳动强度和危险性。因此,研究塔式起重机的定位和防摆控制具有极其重要的理论价值和实际意义。
塔式起重机的定位和防摆控制研究广泛,但也存在不少问题[1-6]。Omar设计全状态反馈控制器,控制小车的定位和起重臂的回转,在一个摆动周期内有效抑制载荷摆动,但系统鲁棒性较差。S.Chatterjee将速度反馈应用到起重机的回转和变幅运动,然而执行时间较长。Jorg Neupert设计了鲁棒控制器,控制塔机的回转运动,但未考虑其变幅运动。张晓华提出了基于输入整形的前馈开环消摆控制策略,但抗干扰性能也较差。
滑模控制设计方法简单,鲁棒性强,所以国内外学者针对不同的系统、不同的控制要求对滑模控制方法进行研究[7-9]。近年来,分数阶微积分理论成为研究热点,用分数阶模型来描述的动态系统要比整数阶模型所描述的更加精确,并可以使系统获得更理想的控制效果[10-14],但分数阶微积分的研究目前还处在初级阶段,在实际工程方面的应用比较少。
针对上述问题,本文考虑塔机的回转运动和变幅运动,提出分数阶滑模控制方法,设计两层分数阶滑模平面,分别控制小车的位移、起重臂的回转角及负载的摆角。系统能快速趋近滑模面,降低滑模抖振,并实现塔式起重机小车的精确定位和负载的消摆。
1塔式起重机的数学模型
塔式起重机的简化模型如图1所示[15]。
进行线性化,得到其动力学模型为:


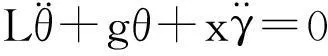
(1)

图1 塔式起重机简化模型
x为臂架小车与塔机中心轴线的垂直距离;M为臂架小车的质量;m为负载的质量;L为绳长;γ为负载旋转的角位移;Tγ为回转转矩;J0为转动惯量;将负载摆角分解为两个分量,φ为绳长在XZ平面上的投影与Z轴的夹角,θ为绳长在XZ平面上的投影与绳长方向的夹角;Fx为沿X方向上臂架小车受的作用力。
令u1=Fx,u2=Tr,式(1)改写为:
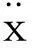

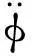
(2)
其中:
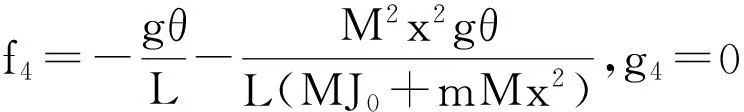
定义误差:

(3)
其中xd,γd,φd,θd分别是x,y,φ,θ的期望值,一般而言,要求φd=0,θd=0.
则系统的误差模型为:
(4)
2分数阶滑模控制
(5)
式中,R(α)是α的实部。分数阶微积分有不同的定义,实际应用中以Caputo定义较为多见。 因此,本文采用Caputo定义:

(6)
Γ(·)是EulerGamma函数,定义为:
(7)
对于系统(4),定义分数阶滑模面为:
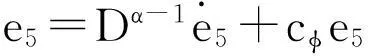
s5=α1s1+β1s3
s6=α2s2+β2s4
(8)
采用等速趋近律,即:
(9)
其中,cx,cγ,cφ,cθ,α1,β1,α2,β2,ε1,ε2是正常数。
为了抑制抖振,选取双曲正切函数代替符号函数。双曲正切函数为:
(10)
根据式(8)-(10)推导可知,系统的分层分数阶滑模控制律为:
(β1h2+β2h4)+ε2g′(s6)(a1h1+α2h3)
u1=___________________________________________
(α1g1+α2g3)(β1h2+β2h4)-(β1g2+β2g4)·
(α1h1+α2h3)
(11)
u2=__________________________________
(12)
β1h2+β2h4
其中Dα-1e(·)由式(6)、(7)定义。
3仿真研究
对上述方法进行仿真研究。塔式起重机系统参数:M=100 kg,m=200 kg,J0=200 kg/m2,g=9.8 m/s2,变幅运动期望值为10 m,回转角期望值为0.5 rad.取微积分的阶次α=0.8,μ=5,控制器参数cx=1.5,cγ=3,cφ=1.0,cθ=3.0,α1=1.0,α2=7.5,β1=5.0,β2=8.5,ε1=ε2=7.0,和整数阶滑模控制进行比较,在27 s处给摆角系统加入幅值为0.8的阶跃干扰,仿真结果如图2-3所示。当系统参数发生摄动(不同负载质量)时,也进行了仿真研究,由于篇幅限制,只给出负载摆角的变化曲线,仿真结果如图4所示。

图2 塔式起重机无干扰的仿真结果
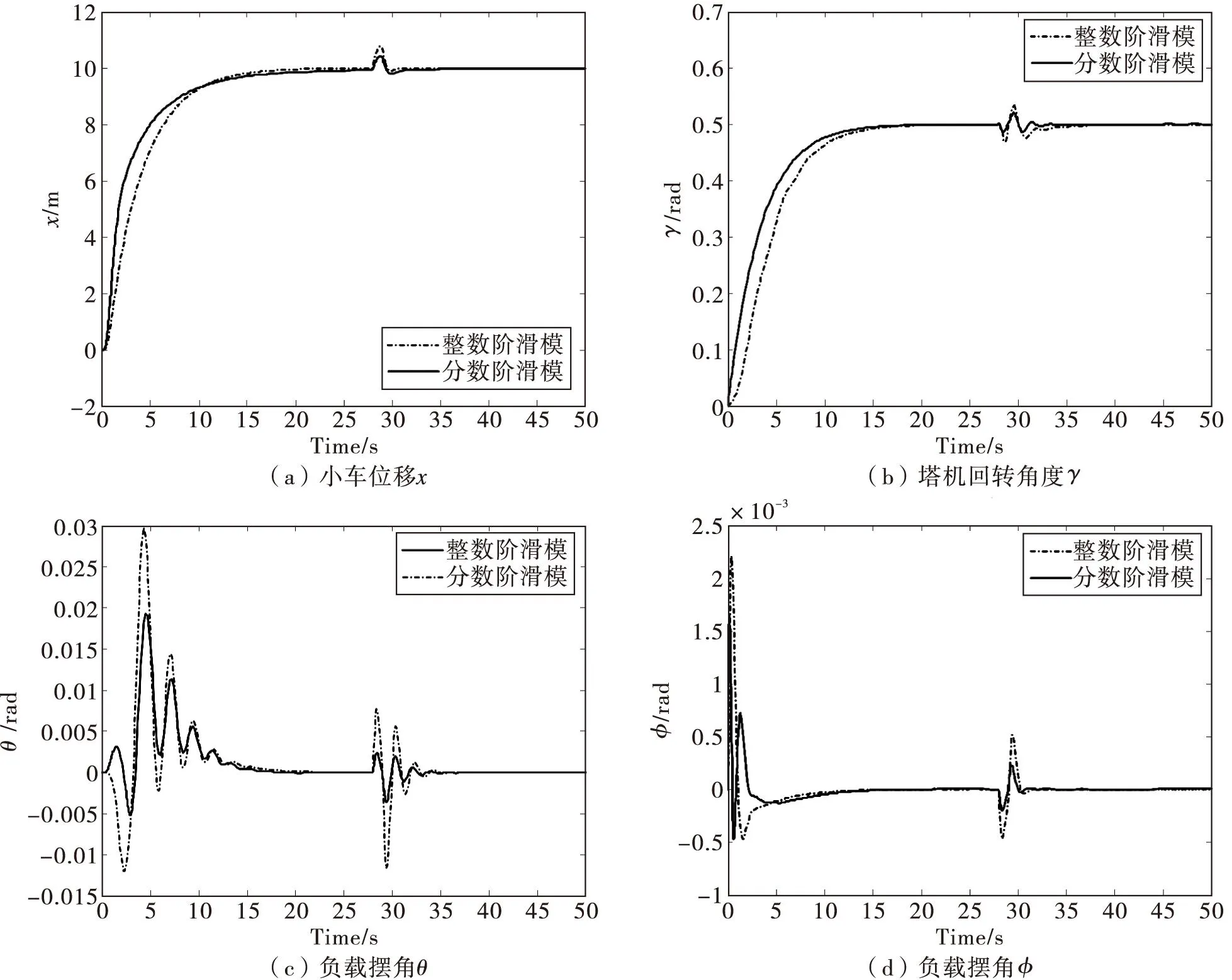
图3 塔式起重机摆角系统加干扰的仿真结果

图4 不同负载质量时负载摆角的变化曲线
从仿真结果可知,基于分数阶的滑模控制与整数阶的滑模控制相比,前者负载摆角φ最大角度仅为0.001 6 rad,θ最大角度仅为0.019 rad,并很快趋于零。而且小车到达期望位置时间也缩短。系统参数发生变化时,负载摆角变化不明显,且加入干扰后,系统能快速到达滑平面,体现出较强的鲁棒性。
4结论
将分数阶微积分理论和滑模控制相结合,提出了分层分数阶滑模控制方法,并应用于塔式起重机的定位和防摆控制。采用分数阶滑模面代替传统滑模面,加快了系统的响应速度,增强了系统的鲁棒性,有效保证塔式起重机小车精确定位和负载的消摆,取得了较好的控制效果。仿真结果也表明此方法的正确性和有效性。
参考文献:
[1]OMAR H M,NAYFEH A H.A simple adaptive feedback controller for tower cranes[C]∥Proc.of 18thBiennial Conference on Mechanical Vibration and Noise,Pittsburgh:American Society of Mechanical Engineers,2001:2611-2621.
[2]S CHATTERJEE.Vibration control by recursive time-delayed acceleration feedback[J].Journal of Sound and Vibration,2008,317(1-2):67-90.
[3]KUNIHIKO NAKAZONO,KOUHEI OHNISHI,HIROSHI KINJIO,et al.Vibration control of load for rotary crane system using neural network with GA-based training[J].Artificial Life and Robotics,2008,13(1):98-101.
[4]JORG NEUPERT,ECKHARD ARNOLD,KLAUS SCHNEIDER,et al.Tracking and anti-sway control for boom cranes[J].Control Engineering Practice,2010,18(1):31-44.
[5]DAVID BLACKBURN,JASON LAWRENCE,JON DANIELSON,et al.Radial-motion assisted command shapers for nonlinear tower crane rotational slewing[J].Control Engineering Practice,2010,18(5):523-531.
[6]张晓华,贾智勇.基于输入整形策略的船上回转吊车防摆控制[J].控制工程,2008,15(3):245-249.
[7]肖敏,史忠科.水雷出水模型突变的控制方法[J].自动化学报,2012,38(10):1609-1617.
[8]BINGLONG CONG,XIANDONG LIU,ZHEN CHEN.Disturbance observe based time-varying sliding mode control for uncertain mechanical system[J].Journal of Systems Engineering and Electronics,2012,23(1):108-118.
[9]MEHMET ONDER.Fractional order sliding mode control with reaching law approach[J].Turkish Journal Electrical Engineering & Computer Sciences,2010,18(5):731-747.
[10]S HASSAN HOSSEINNIA,INES TEJADO,BLAS M VINAGRE,et al.Boolean-based fractional order SMC for switching systems:application to a DC-DC buck converter[J].Signal,Image and Video Processing,2012,6(3):445-451.
[11]MOHAMMAD P A.Finite-time chaos control and synchronization of fractional-order non- autonomous chaotic(hyperchaotic)systems using fractional nonsingular terminal sliding mode technique[J].Nonlinear Dynamics,2012,69(4):247-261.
[12]VINAGRE B M,PODLUBNY I ,HERNANDEZ A,et.al.Some approximations of fractional order operators used in control theory and applications[J].Fractional Calculus and Applied Analysis,2000,3(3):231-248.
[13]HADI DELAVARI DUNITRU BALEANU,JALIL SADATI.Stability analysis of Caputo fractional-order nonlinear systems revisited[J].Nonlinear Dynamics,2012,67(4):2433-2439.
[14]刘舒其,陈志梅,赵志诚.永磁同步电机的分数阶全局快速滑模控制[J],太原科技大学学报,2014,35(3):190-193.
[15]刘晓胜,周进.塔机运行的关键控制算法研究[J].科学技术与工程,2010,10(2):1671-1815.
Fractional-order Sliding Mode Position and Anti-swing Control of Tower Crane
CHEN Zhi-mei,SUN Hui,ZHANG Jing-gang,SHAO Xue-juan
(School of Electronic Information Engineering,Taiyuan University of Science and Technology,
Taiyuan,030024,China)
Abstract:Considering the slewing motion and luffing motion of tower crane,a layered fractional-order sliding mode control method is proposed for tower crane anti-swing control system.It is divided into two subsystems which are the trolley displacement control system and load swing angle control system.A two-layer fractional-order sliding surface is introduced to replace the ordinary sliding surface to control the trolley displacement,the slewing angle of the boom and load swing angle respectively.Compared with the integer-order sliding mode control,the new control scheme accelerates the system response speed,enhances the robustness and improves the control performance.Not only precise positioning but also anti-swing ability are realized with the fractional-order method.Simulation results also show that the fractional-order sliding mode control is an effective method to improve control performance of tower crane system.
Key words:tower crane,slewing,luffing,fractional order,layered sliding mode control
中图分类号:TP273;TH215
文献标志码:A
doi:10.3969/j.issn.1673-2057.2016.01.003
文章编号:1673-2057(2016)01-0012-06
作者简介:陈志梅(1970-), 女,教授,博士,主要研究方向为机电一体化系统控制。
基金项目:山西省自然科学基金(2014011020-2、2014011020-1);山西省研究生教改项目(20142058);太原科技大学教改项目(20133014)
收稿日期:2015-05-08
