多孔板等效弹性常数的均匀化预测及实验研究
2016-03-03晋艳娟李盛静崔小朝
杨 昆,晋艳娟,李盛静,崔小朝
(太原科技大学应用科学学院,太原 030024)
多孔板等效弹性常数的均匀化预测及实验研究
杨昆,晋艳娟,李盛静,崔小朝
(太原科技大学应用科学学院,太原 030024)
摘要:基于均匀化方法,对多孔板的宏观等效弹性常数进行预测,得到了面内的弹性模量、泊松比和剪切模量。然后通过拉伸实验的方法,对多孔板进行拉伸性能测试,得到了应力应变曲线,并将实验得到的弹性模量与均匀化方法计算得到的弹性模量进行比较。结果表明,均匀化方法计算得到的等效弹性模量与实验得到的结果相吻合,验证了均匀化方法预测多孔板弹性常数的可行性。
关键词:均匀化方法;多孔板;等效弹性常数;实验研究
多孔板类结构在各类核电设备、换热设备中应用十分广泛,其特点是在结构中周期性分布着许多小孔,这些小孔的尺寸与整体的多孔板的尺寸相比小得多。在对周期性分布小孔的多孔板结构进行有限元分析时,将圆孔多孔板当量化成均质实心板是一种有效的方法[1]。这种均质的实体板,即当量板,必须具有与实际开孔板等效的弹性常数。文献[1]总结了当量板弹性常数的求解方法,给出了常见圆孔板有效弹性常数工程设计公式[2],但多数是通过实验方法得到的。对于圆孔多孔板,由于其研究方法、建立的模型不同,得到的结果也存在差异。
均匀化理论(homogenization)于20世纪70年代由法国科学家提出[3-4]。一直以来,该方法被认为是复合材料、混凝土材料当量性能的常用手段之一。该理论也可应用于计算多孔板的宏观等效弹性常数[5-7]。因此,本文基于均匀化方法对圆孔多孔板的等效弹性常数进行预测,得到圆孔板的等效弹性模量,然后通过实验方法测得面内弹性模量,将计算结果与实验结果进行比较,证明均匀化方法的正确性。
1均匀化方法及其有限元列式
均匀化方法是一种用于分析周期性微观结构材料性能并且经过严密的数学推导的方法。它由材料的微观结构“胞元”出发,将胞元均匀化方法引入到宏观和微观尺度中,采用摄动技术建立了宏细观之间的联系,由一个细观单胞进而得到整体材料的宏观性能。因此,周期性微观结构在周期性边界条件下等效弹性常数的计算表达式为:
(1)
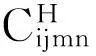
由于周期性结构材料为横观各向同性,弹性系数矩阵为对称矩阵[Cijmn],且Cijmn用紧缩形式Dij表示,则有:
[Cijmn]=D=[d1,d2,d3,d4,d5,d6]
(2)
同时定义:
(3)
(4)
代表单元体为横观各向同性材料,微分ε(χmn)可表示为:
利用有限单元离散代表单元体,选取四面体单元作为离散单元,对于任意单元,利用相应的插值函数分别对χkl,ε(χkl),v,ε(v)进行插值:
(5)
(6)

根据式(2)-(6),方程(1)可分别化为:
(7)
(8)
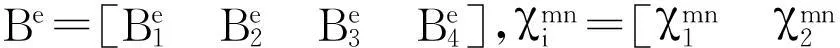
(9)
则方程(7)可化为:
(10)
节点虚位移u可以任意取值,方程(10)简化为:
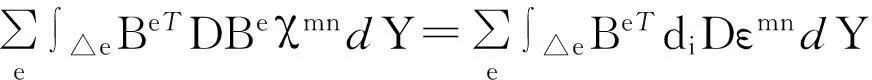
(11)
2多孔板的弹性常数预测
2.1 多孔板有限元模型的建立
正四边形和正三角形的排列方式在多孔板结构的实际运用中较为常见,如图1所示。根据购买的如图1(b)所示的排列方式的圆孔多孔板建立有限元分析模型,如图2所示,具体模型尺寸见表1.根据单胞排列的对称性和单胞的周期性边界条件的要求,图中阴影部分即为1/4单胞有限元分析的计算区域。
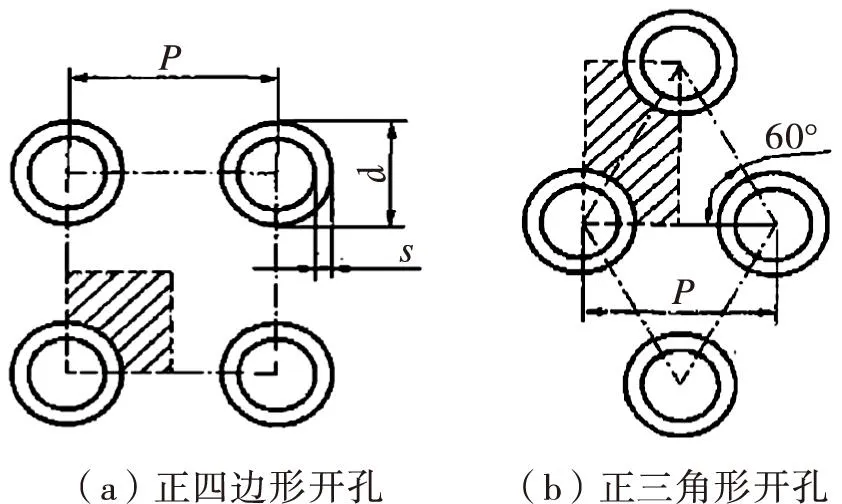
图1 多孔板开孔的分布规律

图2 有限元分析模型
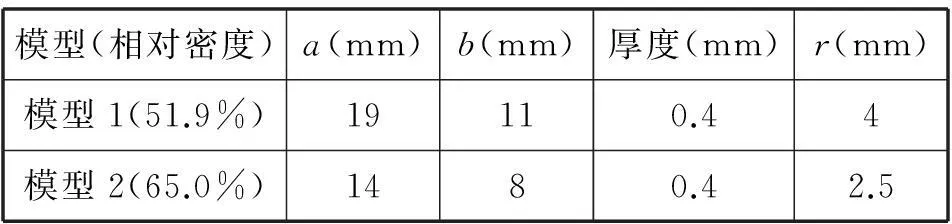
模型(相对密度)a(mm)b(mm)厚度(mm)r(mm)模型1(51.9%)19110.44模型2(65.0%)1480.42.5
利用Abaqus有限元软件建立单胞的实体及有限元模型,其单元类型采用四面体单元。在有限元分析模型的建立过程中,首先建立单胞模型的1/4并对其划分网格,然后再将网格部件进行对称复制操作,从而保证所有节点位置的完全对应。多孔材料的弹性常数为:E=32.46 GPa,v=0.25.
2.2 周期性边界条件的确定
对细观单胞进行有限元求解时,需要满足周期性边界条件。采用建立点对点的约束方程、施加顶点零位移自由度的方式来实现周期性边界条件在Abaqus软件中的加载。若用u,v和w分别表示等效位移χ在y1、y2和y3三个方向的位移分量,那么周期性边界条件如式(12)所示。
(12)
2.3 计算结果
将有限元计算的结果,运行均匀化方法计算宏观弹性矩阵的程序,得到多孔板的弹性张量CH(单位:GPa).进而得到多孔板面内的宏观弹性常数见表2.
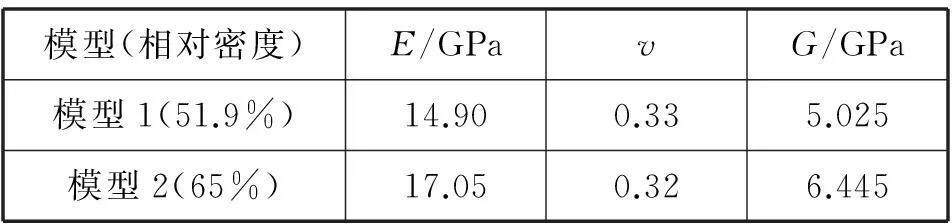
表2 多孔板的宏观弹性常数
由表2可知,随着相对密度的增大,面内的弹性模量越大,剪切模量也越大,即随着相对密度的增大,面内的弹性模量和剪切模量都呈现逐渐增加的趋势。
3多孔板材料性能的实验研究
3.1 试验试样及实验装置
选择孔径大小不同的两种的圆孔多孔板进行试验,试样1长宽为:110 mm×19 mm ,孔半径为4 mm,试样2的长宽为:80 mm×14 mm,孔半径为2.5 mm.实验装置采用XWW-20A型电子万能材料实验机。
3.2 多孔板拉伸实验
试验选择两组孔径大小不同的试件。夹好试件后,采用位移控制在多孔板y方向缓慢加载直至多孔板断裂。实验完成后,圆孔半径为4 mm的圆孔多孔板的一组应力-应变曲线如图3所示。
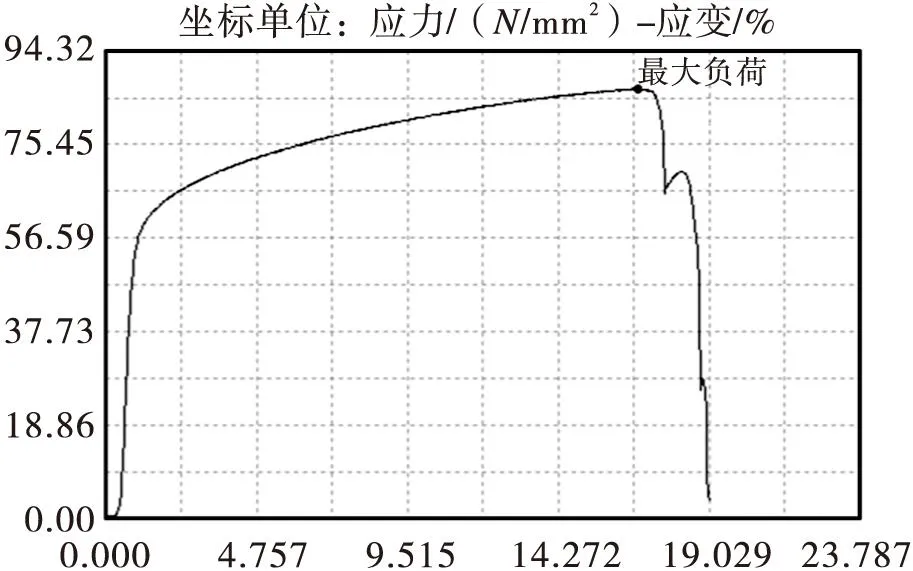
图3 圆孔直径8 mm多孔板的应力-应变曲线
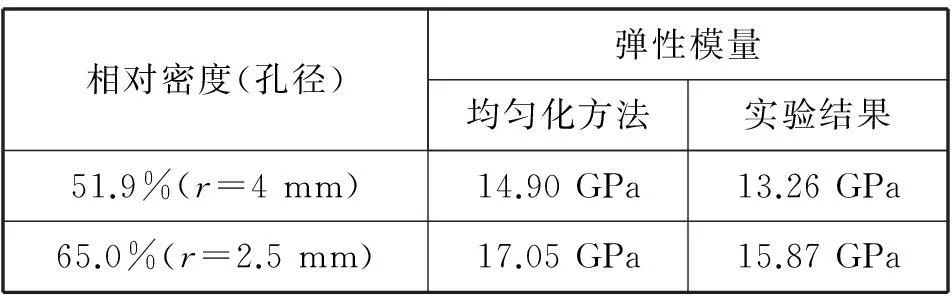
相对密度(孔径)弹性模量均匀化方法实验结果51.9%(r=4mm)14.90GPa13.26GPa65.0%(r=2.5mm)17.05GPa15.87GPa
通过多次试验求平均的方法,得到不同孔径的多孔板的弹性模量,孔半径为4 mm的多孔板的弹性模量为13.26 GPa,孔半径为2.5 mm的多孔板的弹性模量为15.87 GPa.由模拟结果与实验数据平均值(表3)的比较发现均匀化方法的计算结果与实验数据基本吻合。结果表明,均匀化方法可以用于预测圆孔多孔板的等效弹性模量。
4结论
利用均匀化方法对圆孔多孔板的等效弹性性能进行预测,得到了多孔板的等效弹性常数,其面内等效弹性模量的预测结果与实验结果基本吻合,说明均匀化方法预测圆孔多孔板等效弹性模量的正确性。随着相对密度的增大,弹性模量和剪切模量逐渐增大。
参考文献:
[1]OSWEILLER F.Evolution and Synthesis of the Effective Elastic Constants Concept for the Design of Tubesheets[J].Journal of Pressure Vessel Technology,1989,111(3):209-217.
[2]JAMESR FARR,MAANH JAWAD.ASME压力容器设计指南[M].北京:化学工业出版社,2003.
[3]PALEY M,ABOUDI J.Micromechanical analysis of composites by the generalized cells model[J].Mechanics of Materials,1992,14(2):127-139.
[4]GHOSH S,LEE K,MOORTHY S.Multiple scale analysis of heterogeneous elastic structures using homogenization theory and Voronoi cell finite element method[J].International Journal of Solids and Structures,1995,32(1):27-62.
[5]汪荣鑫.数理统计[M].西安:西安交通大学出版社,1986.
[6]龚曙光,陈艳萍,谢桂兰.均匀化理论在多孔板结构优化中的应用研究[J].机械科学与技术.2004,23(8):995-998.
[7]HASSANI B,HINTON E.A review of homogenization and topology optimization I—homogenization theory for media with periodic structure[J].Computers & Structures,1998,69(6):707-717.
Homogenization Predication of Equivalent Elastic Modulus for Perforated Plates and Experimental Research
YANG Kun,JIN Yan-juan,LI Sheng-jing,CUI Xiao-chao
(School of Applied Sciences,Taiyuan University of Science and Technology, Taiyuan 030024,China)
Abstract:The equivalent elastic modulus of perforated plates can be predicted based on homogenization theory,and the in-plane elastic modulus,Poisson′s ratio and shear modulus can be achieved.Then the tensile property of perforated plates can be tested with tensile experiment method, and the stress-strain curves were got.The elastic modulus obtained by experiment method is compared with that calculated by homogenization method.The results show that the elastic modulus calculated by homogenization theory is consistent with that obtained by experiment,and it is verified to be feasible to predict elastic modulus of perforated plates with homogenization method.
Key words:homogenization method,perforated plates,equivalent elastic constant,experimental research
中图分类号:TB383
文献标志码:A
doi:10.3969/j.issn.1673-2057.2016.01.017
文章编号:1673-2057(2016)01-0077-04
作者简介:杨昆(1993-),男,主要研究方向为工程问题的数值解法;通讯作者:晋艳娟,博士,讲师,E-mail:jinyanjuan2003@163.com
基金项目:山西省高等学校大学生创新创业训练项目(2014261);校级大学生创新创业训练项目(xj2014019);山西省基础研究项目(2015011002,2015021021)
收稿日期:2015-04-17
