基于非线性平滑转换回归模型的我国“费雪效应”检验
2016-03-02彭文兵严国津
彭文兵 严国津
内容摘要:本文通过引入非线性平滑转换回归方法,并基于我国1990年12月-2015年1月的月度时间序列数据,实证检验我国以“一年期贷款利率”和“一年期居民定期存款利率”为代理的名义利率与通货膨胀率之间是否存在“费雪效应”。研究表明:相较于线性模型,利用平滑转换模型更能准确把握我国名义利率和通胀水平两者之间的关系;我国存在较弱的费雪效应,且该效应在不同的通胀状态下存在显著的非对称性,其中通胀紧缩和高通胀状态相对温和,通胀状态有较大水平的减弱;此外,一年期居民定期存款利率与通胀水平的费雪效应要强于一年期贷款利率与通胀水平之间的费雪效应。最后,分析了实证检验所蕴含的政策含义并提出政策建议。关键词:费雪效应 非线性平滑转换回归 名义利率 通货膨胀率
研究概述
名义利率与通货膨胀率两者之间关系的研究始于英国古典学派经济学家费雪。他在被经济学界称之为“费雪效应”的这一理论假设中指出:在市场信息可以充分预见的前提下,名义利率与通货膨胀率两者之间表现出一一对应的变动关系,通货膨胀的变动可以由名义利率的变动完全反映出来,从而名义利率与通货膨胀率之差即实际利率将保持不变。费雪效应具有明显的政策涵义,可以以其为标准用来判断货币政策等作用机制:若存在完全的费雪效应,则表明货币幻觉并不存在、货币政策具有超中性,政府通过货币政策来影响实际利率进而干预经济活动仅能导致名义经济变量同比例的变动,而对就业等实际变量不会产生影响;此外,费雪效应的存在还表明可以利用名义利率来预测通货膨胀预期。因此,研究是否存在费雪效应,不仅在理论上具有重要价值,而且具有重要的现实意义,因而成为国内外学术界的一个热点问题。
尽管费雪效应在提出之后,在理论上被普遍接受,且许多经济学和金融学模型以其为基本假设而展开分析。但现有基于计量经济学方法的实证研究结果与理论假设存在很大差异,并没有得到统一的结论,即存在所谓的“费雪悖论”。协整理论自20世纪80年代提出并得以广泛使用后,检验是否存在费雪效应的一个主要切入点就是利用协整理论和误差修正模型来分析名义利率和通货膨胀率两者之间的长期均衡关系和短期动态调整及因果关系。如Mishkin(1992)基于美国1953-1990年月度时间序列,发现美国名义利率与通货膨胀率均为I(1)序列,两者之间存在显著的长期费雪效应,而短期费雪效应并不存在。Granville和Mallick(2004)基于1900-2000年度数据,运用JJ协整检验发现英国名义利率与通货膨胀率之间在长期内存在完全的费雪效应。
协整理论等计量方法亦被应用到我国费雪效应的检验之中,如:刘康兵等(2003)基于我国1979-2000年的名义利率和通胀数据,分别利用完全修正自回归分布滞后模型和广义矩估计法分析长期和短期费雪效应,发现长期和短期费雪效应均存在。王信文等(2005)运用虑及结构突变的ADF单位根检验模型以我国台湾地区为对象,发现样本期内并不支持费雪效应的存在。王少平等(2008)应用非参数单位根和非参数协整理论对我国1990年1月至2007年4月的月度数据进行了检验,结果表明我国存在弱的费雪效应。
上述文献均是在名义利率与通胀水平之间为线性关系的前提下进行的,然而近年来随着非线性理论的不断发展,越来越多文献表明名义利率和通货膨胀率之间的长期关系应为非线性。封福育(2009)基于我国月度数据,利用多元门限回归模型分析了我国一年期贷款利率与通胀水平之间的关系,其研究结论表明不同的通胀水平下两者关系并不一致。陈海燕等(2010)利用门限协整理论对我国费雪效应进行了再检验,其结论也支持上述非线性关系。需要指出的是,封福育和陈海燕的研究中所用的非线性调整在不同机制间的转换为非连续的,而Granger(1993)的研究结果表明,大多数经济变量在不同机制间的转换过程往往为一个连续平滑过渡的过程。而新近发展起来的非线性平滑转换回归(STR)方法能够刻画经济变量在两个不同区制间连续平滑的转换,且已被广泛地应用于经济、金融等领域。因此,本文将借助STR方法,实证检验不同通胀水平下我国名义利率与通货膨胀率之间的关系。
模型与数据
(一)理论模型
费雪效应可用以下形式的费雪方程来说明:
Rt = rt + E(πt) (1)
其中:Rt是名义利率,rt为事前实际利率,E(πt)为预期通货膨胀率。
Fama(1975)认为费雪方程中的实际利率取决于经济中的实际因素而与预期通货膨胀无直接关系,因此可以将实际利率rt视为常数,即rt = r;此外,由理性预期假说可知,人们对通货膨胀率预期是无偏的,即成立πt = E(πt) + εt,其中εt为服从怀特白噪声过程的随机扰动项。因此,可以得到用于实证检验费雪效应是否存在的线性回归模型:
Rt = r + απt + ηt (2)
其中:ηt为非预期的误差成分,α为通货膨胀率对名义利率的弹性系数,若α=1,说明存在完全的费雪效应;若0<α<1且参数估计显著,则表明存在部分或较弱的费雪效应。
(二)基于STR方法的实证检验模型
如前所述,之所以出现“费雪悖论”,其原因在于没有考虑到名义利率与通货膨胀率之间可能存在非线性关系。同时考虑到STR方法自身的优越性,本文设计以下实证模型来检验名义利率与通货膨胀率在不同通胀水平下所可能呈现的不同关系:
Rt = r1+α1πt+(r2+α2πt)F(γ, c,πt)+et (3)
F(πt,γ,c)为平滑转换函数,其值介于0-1之间。其中,参数γ>0表示平滑参数,表示经济变量从一个区制转换到另一个区制速度的快慢以及调整的平滑性;而参数c为门槛参数,用来表示两个区制的转换位置。et为随机误差项。
现有文献中转换函数F(πt,γ,c)通常采用LSTR1模型、LSTR2模型或ESTR模型三种形式,其对应的表达式分别为:
LSTR1:F(γ,c,πt)={1+ exp[-γ(πt - c)]}-1 (4)
LSTR2:F(γ,c,πt)={1+ exp[-γ(πt- c1)(πt - c2)]}-1 (5)
ESTR:F(γ,c,πt)=1 - exp[-γ(πt - c)2],c1≤c2 (6)
通过引入以通货膨胀率πt为转换变量的非线性平滑转换函数F(γ,c,πt),能够考察名义利率和通货膨胀率在不同通胀水平下是否有不同的关系、以及在不同状态间转换的速度。STR模型较之线性模型能够更为准确刻画现象背后所反映的经济规律。
(三)数据及其描述统计
为减少估计的偏误本文采用月度数据进行实证分析,同时考虑到数据的可获得性,样本区间选择为1990年12月至2015年1月,样本容量为284个数据。其中,通货膨胀率以居民消费物价指数CPI的同比变化率来表示,即:
πt = (CPIt - CPI t-12) *100%/ CPI t-12 (7)
为更全面的考察费雪效应,并与现有文献进行比较,同时选择一年期贷款利率和一年期居民定期存款利率作为名义利率,分别记为DRt和CRt。本文所用数据来源于中国统计局国家数据和中国人民银行网站。
实证及结果分析
(一)单位根检验及线性协整检验结果
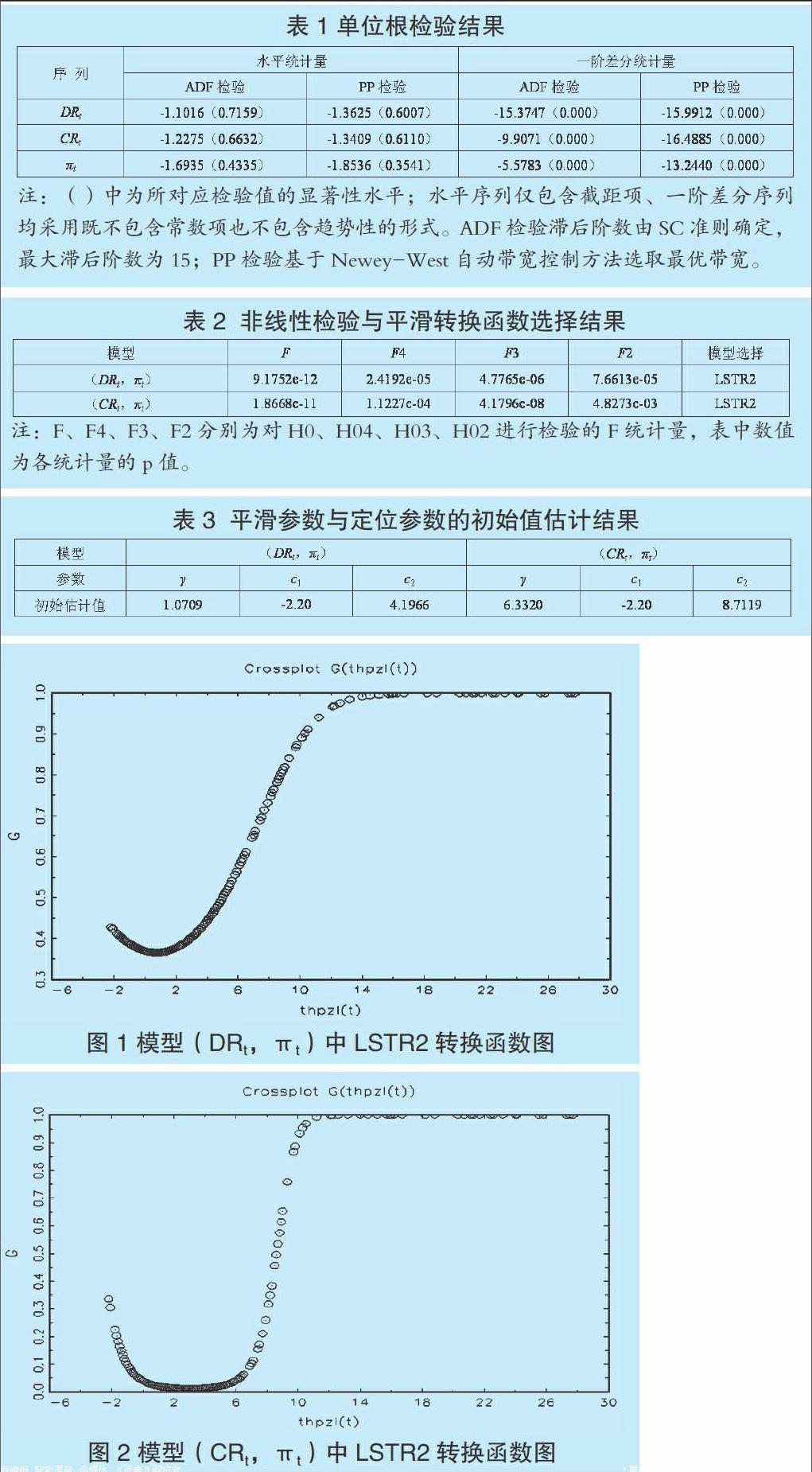
在检验费雪效应之前,需要检验名义利率和通货膨胀率的平稳性,以确定其单整阶数。本文同时采用ADF和PP单位根检验方法,其结果见表1。
表1中ADF检验和PP检验都表明:DRt、CRt和πt在10%的显著性水平下均为非平稳,但其对应的一阶差分序列均在1%显著性水平下平稳。因而可以利用E-G两步法对名义利率和通货膨胀率是否存在长期协整关系进行检验。为此分别对(DRt,πt)和(CRt,πt)进行线性回归,可以得到(方括号内的数字为对应系数t值,下同):
DRt=6.06554+0.25011πt+η1t (8)
(19.2417)
AD-R2=0.5661,AIC=3.4628,SC=3.4885,HQ=3.4731
CRt = 2.81598+0.39503πt+η2t
(22.1537) (9)
AD-R2=0.6306,AIC=4.1667,SC=4.1941,HQ=4.1777
对(8)、(9)式的残差进行单位根检验,可知(8)和(9)式的残差均在5%显著性水平下平稳,故DRt和CRt均与通货膨胀率存在长期协整关系,且从系数大小可以看出,均表现为部分费雪效应的存在。
(二)非线性检验及平滑转换函数选择
本部分将基于Terasvirta所提出的序贯检验程序检验当以通货膨胀率πt为转换变量时,我国名义利率与通货膨胀率是否存在显著的非线性转换特征。为此,先将转换函数F(πt,γ,c)在γ=0状态下进行泰勒展开,代入模型(3)可得以下形式的辅助回归:
Rt = ztb0 +πt2b1 +πt3b2 +πt4b3 +e*t
(10)
其中,zt = (1,πt),e*t = et+R3(γ, c,πt) ( r2+α2πt), R3(γ, c,πt)为转换函数泰勒展开式的余项。在(10)式的基础上对原假设H0:b1=b2=b3=0进行基于F统计量的检验,若拒绝原假设,则表明存在非线性关系。可通过检验下述假设选择平滑转换函数形式:
H04:b3=0
H03:b2=0|b3=0
H02:b1=0|b2=b3=0
若F统计量的相伴概率p值强烈拒绝H03,则平滑转换函数选择LSTR2或ESTR模型;否则,选择LSTR1模型。由表2检验结果可以发现,对于模型(DRt,πt)和(CRt,πt),其接受线性假设的概率均远小于1%,故拒绝原假设,即两者之间存在非线性关系。两模型转换函数均选择LSTR2。
(三)STR模型估计结果及分析
为估计模型参数,先利用格点搜索法估计STR模型中平滑参数γ及定位参数c的初始值,其中γ的取值范围为[0.5,10],c为[-2.20,20],将这两个区间均60等分得到3600个组合,取使得残差平方和最小值所对应的组合为初始值,其结果见表3。
表3显示的初始估计值均落在事先确定的取值范围之内,在此基础上,本文利用带有数值导数的BFGS算法来估计STR模型参数,详细步骤可参照Hendry(1995),此处不再赘述。逐步剔除不显著的变量,得到模型(DRt,πt)的最终估计结果为:
DRt=3.1360+0.097πt+( 7.7290-0.0911πt) {1+exp[-1.1725(πt+3.5459)(πt - 5.0109)]}-1+e1t (11)
AD-R2=0.6525,AIC=0.4451,SC=0.5350,HQ=0.4811
模型(CRt,πt)的最终估计结果为:
CRt=2.3677+0.3935πt+( 6.7342-0.3124πt){1+exp[-5.4209(πt+2.6511)(πt-8.6129)]}-1+e2t (12)
AD-R2=0.7064,AIC=1.0784,SC=1.1683,HQ=1.1145
对(11)(12)式的残差进行单位根检验,可知(11)(12)式残差均在1%显著水平下平稳,表明样本期内我国名义利率与通货膨胀率确实存在阈值协整关系。
此外,比较(8)和(11)式,发现AD-R2由线性模型的0.5661提升至LSTR2模型的0.6525,而AIC、SC和HQ判断准则均大幅度减少;比较(9)和(12)式,在AD-R2值由0.6306提升至0.7064的同时,三个判断准则亦有较大幅度的降低。上述结果表明,非线性STR模型能够更为准确的反映我国名义利率与通货膨胀率之间的内在依从关系。
图1和图2揭示了由于通胀水平的不同所导致的名义利率与通货膨胀率之间关系具有区制转换的非线性特征。
结合图1和(11)式发现:转换函数中的两个门槛值为c1=-3.5459,c2=5.0109,转换函数关于(c1+c2)/2=0.7325对称,当通胀水平πt=0.7325%时,此时转换函数F(γ,c,πt)为0,故模型所显示的为完全的线性形式。而当通胀水平πt小于-3.5459%或大于5.0109%,即当出现通胀紧缩或高通胀状态时,函数值将以γ=1.1725的速度向1转换,体现出不同通胀水平对以“一年期贷款利率”为代表的名义利率影响的非对称性。当处于温和通胀状态时(πt在-3.5459%与5.0109%之间),通胀水平对名义利率的影响作用体现出较为稳定的线性关系,当通货膨胀率每上升1%,“一年期贷款利率”将提高0.097%。当处于通胀紧缩或高通胀水平时,通货膨胀率每上升1%,“一年期贷款利率”将相应提高0.0059%。
由图2和(12)式可知:当以“一年期居民定期存款利率”作为我国名义利率的代理指标时,当通胀水平为πt=(c1+c2)/2=2.9809%时,转换函数F(γ, c,πt)为0,名义利率和通胀水平之间的关系为完全的线性形式;此时,当通货膨胀率小于-2.6511%或大于8.6129%时,函数值将以γ=5.4209的速度向1转换,由此表明“一年期居民定期存款利率”对不同通胀水平的非对称性反映。具体的,当处于通胀紧缩或者高通胀水平时,通货膨胀率每上升1%,“一年期居民定期存款利率”将相应提高0.0811%;当通货膨胀率介于两者之间时,通货膨胀率每上升1%,“一年期居民定期存款利率”将提高0.3935%,两者之间体现出较为稳定的线性关系。
以上结论表明,无论以“一年期贷款利率”还是“一年期居民定期存款利率”作为我国名义利率的代理指标,我国均存在较弱的费雪效应,且这一效应在通货紧缩或高通胀的情况下有很大程度的降低,该结论与封福育(2009)的结论有一定的类似之处。进一步比较(11)和(12)式发现:从费雪效应程度来看,一年期贷款利率相对一年期居民定期存款利率而言要更弱;另一方面,从模型的转换速度来看,一年期存款利率要大于一年期贷款利率(γ=5.4209>1.1725),表明当通胀水平进入极端状态,相对贷款利率而言,存款利率将以较快速度做出相应的反应。其原因可能在于:虽然我国较早开始了利率市场化的改革,但在实践中我国名义利率并非是根据市场价格信号做出相应的反应,而往往是中央银行根据我国经济发展的需要进行主动调整,由于利率政策的制定及实施是通过行政指令下达,存在较长的时滞,使得名义利率难以对预期通胀水平的变动做出有效的反应,最终导致市场参与者对预期通胀水平的估计存在较大偏差,也进一步弱化了费雪效应在我国的存在,而这一现象在通胀水平极端情况下更为明显。
结论
准确把握名义利率和通胀水平两者之间的数量关系,分析是否存在费雪效应,是进一步制定货币政策并实施的重要基础。为此,本文在分析现有研究我国费雪效应的文献基础上,将新近发展起来的非线性平滑转换回归方法引入至费雪效应研究中。并基于我国1990年12月至2015年1月的月度数据,分别利用“一年期贷款利率”和“一年期居民定期存款利率”作为名义利率的代理指标,以“居民消费物价指数CPI的同比变化率”来衡量通胀水平,实证分析了我国名义利率与通货膨胀率两者之间的数量关系。各种判别准则表明,相较于线性模型,基于非线性平滑转换回归模型更能准确刻画两者之间的关系。进一步的实证检验结果表明,我国存在较弱的费雪效应,且该效应在不同的通胀水平下存在非对称性,并且一年期贷款利率和一年期存款利率对投资水平的反应存在较大的差异,具体的:当通货膨胀率上升1%,在温和通胀状态下,一年期贷款利率将提高0.097%、而一年期存款利率将提高0.3935%;而在通胀紧缩或高通胀水平下,一年期贷款利率仅提高0.0059%、一年期存款利率相应提高0.0811%。
以上结论表明,我国现行利率政策并没有与市场经济的发展完全相适应,缺乏有效的传导机制,使得利率对市场价格的变动反应较为微弱;与此同时,名义利率也难以灵活地传导货币政策,使得市场参与者无法根据名义利率的变动做出合理的通货膨胀预期。因此,需要进一步促进利率市场化,以在我国逐步建立起以利率指标作为中介目标的货币政策,使得名义利率能够灵活真实地传导货币政策,同时也能及时准确对通货膨胀水平的变动做出有效的反应。
参考文献:
1.刘康兵,申朴,利达.利率与通货膨胀:一个费雪效应的经验分析[J].财经研究,2003,29(2)
2.王信文,吴幸芳.市场结构反转下的费雪效应研究[J].当代经济科学,2005,27(4)
3.王少平,陈文静.我国费雪效应的非参数检验[J].统计研究,2008,25(3)
4.苏芳,周璐,蔡经汉.中国经济费雪效应再检验:基于两区制门槛协整模型的实证研究[J].安徽大学学报(哲学社会科学版),2010(5)
5.封福育.名义利率与通货膨胀:对我国“费雪效应”的再检验—基于门限回归模型分析[J].数量经济技术经济研究,2009(1)
6.陈海燕,李松臣.中国费雪效应的门限协整检验[J].统计与信息论坛,2010,25(2)
