基于有限元仿真的细长导轨加工变形与误差补偿技术

王小龙，王爱民，吕艳鹏

（北京理工大学 机械与车辆学院数字化制造研究所，北京 100081）

0 引言

在航天航空制造业中，整体薄壁件因其强度高、可靠性好等优点被广泛使用。细长导轨工件纵向尺寸大，截面尺寸小，尺寸精度要求高，是一种典型的整体薄壁件。细长导轨通常长达数米，但截面尺寸最薄处只有几毫米厚，且形状复杂，使得其装夹困难，局部刚度强弱不一。细长导轨的加工通常采用铣削加工，以小切深、慢进给的方式减小加工变形，但是由于刚度弱而导致的让刀变形仍然很明显，使得加工后导轨直线度与平面度不达标，是加工变形的主要因素。针对让刀变形，可以通过误差补偿技术来减小。

国内外对误差补偿技术的研究已取得一些成果，国外学者Ratchev等[1]研究了薄壁件铣削加工时刀具、工件变形耦合效应的柔性预测方法及其误差补偿方法。Weinert等[2]通过限元方法对铝合金薄壁件周铣过程中静态误差进行了预测。国内学者赵欣等[3]研究了薄壁叶片加工变形模型预测与误差补偿，模拟了不同切削参数对工件变形产生的影响，王光宇等[4]采用自适应网格技术对铣削加工变形和走刀路径对加工变形的影响进行了分析，陈双喜[5]对壁圆筒零件车削加工变形进行了补偿计算；尹飞鸿[6]等研究了薄壁框铣削变形预测。

虽然现有研究较多，对小型加工件的误差补偿技术较成熟，但是在对大型薄壁零件，比如细长导轨件的研究还是空白。现有研究多集中在对切削过程的模拟，通过对真实刀具与工件进行三维建模，并对其有限元切削模拟结果进行分析，从而指导实际生产。为了使得结果精确度高，可以对加工部分的网格进行密化，或使用自适应网格技术，这在小型工件的加工过程模拟中是很好实现的，但是对于细长导轨类大型工件，密化网格将使得网格数量大幅增加，这将导致显式切削计算量变得非常庞大，单次计算求解时间长达数周，研究周期长。因此，针对大型工件，需要探索新的误差补偿方法，本文从细长导轨工件加工的误差补偿技术入手，提出了一种适合于大型工件的误差补偿方案。

通过对细长导轨上每个采样点施加切削力来获取该采样点的加工变形，并通过镜像误差补偿理论获取刀具补偿轨迹，最后通过实际加工验证了该误差补偿技术的准确性。

1 细长导轨表面加工变形误差补偿解决思路

对铣削过程模拟的首要任务就是对铣削力的获取，查阅机械加工工艺手册[5]，可以获得刀具对工件作用的铣削力经验公式，经验公式求得的结果可作为参考，本文通过运用Abaqus有限元通用软件对真实尺寸的刀具进行三维切削仿真来获取细长导轨加工过程的铣削力，并与铣削力经验公式进行对比，定量的判断仿真结果的准确性。

获取铣削力后，可以将其施加在导轨加工面的采样上，利用隐式静力学分析，获取整个导轨的静态响应。考虑到加工过程的动态性，只有施加铣削力的采样点处的变形是精确的，因此，对此该铣削力载荷的静力结果，仅取出施加铣削力采样点的变形数据。然后对下一个采样点施加铣削力，获取该采样点变形数据，直至最后一个采样点。虽然该方法需要对每个采样点施加一次载荷并求取结果，分析步数量很多，但是其每一步的分析所需要的时间成本是很低的，实践证明，针对该细长导轨的分析仅需3小时即可完成。运用该方法的另一个难点就是需要对每个采样点设置一个分析步，工作量很大，解决的方法是对Abaqus进行二次开发[7]，通过Python语言编写的脚本可以很方便的完成分析步和载荷的施加。

针对本文所述细长导轨工件，需要设置采样点提取数据，通过分析加工工艺，设置了7个采样面，每个采样面上分布有若干条采样线，共49条，每条采样线沿导轨纵向延伸，均包含102个采样点，共4998个采样点，如图1所示。

图1 导轨采样面、线、点分布

通过切削力求解方法，分别计算采样面上的铣削力，将求得的切削力通过隐式静力学分析作用到采样面的采样点上，并求取采样点处的加工变形。依次对每个采样点分析，获取数据，并通过MATLAB对数据进行展示与分析。然后通过镜像误差补偿理论，即可获取刀具补偿轨迹，最后通过实际加工，验证该方法的可行性，该方法的流程图如图2所示。

2 细长导轨表面加工过程建模与仿真

2.1 切削力经验公式计算

通过查阅金属切削手册，可以知道铣削力的经验公式如下：

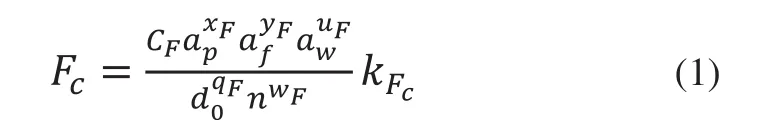
图2 加工变形误差补偿流程

其中ap为背吃刀量，af为每齿进给量，aw为铣削切削层公称宽度，d0为铣刀直径，n为铣刀转速取，其余为切削其他参数。结合实际加工工艺数据，即可求取切削力大小。例如细长导轨采样面1加工刀具为面铣刀，材料为硬质合金，n=2000r/min，d0=60mm，af=0.216mm/齿，ap=2mm，aw=53mm，查找铣削力参数表可知，CF=7750，xF=1.0，yF=0.75，uF=1.1，wF=0.2，qF=1.3，kFc=0.55，带入式(1)得：

即通过经验公式求得的切削力为227.2N。

2.2 铣削力有限元仿真求解过程

铣削力有限元仿真的求解要求刀具采用真实切削刀具尺寸，工件可以选用块状工件，材料属性为真实工件材料属性即可。该细长导轨面1加工采用面铣刀，面铣刀主要用于工件表面的铣削，本文建立了典型的面铣刀三维模型，材料为硬质合金SMP，直径60mm，周部6个刀刃，刀刃前角14°，后角9°。工件材料为2A12铝合金，切削力求解工件模型为60*60*20mm的块状件。

切削本构模型采用Johnson - Cook材料模型，该模型能有效的模拟应变率效应和温升软化效应，通过力-热耦合使得求解出的铣削力更加准确。具体表达式如式3所示。

张伟等[8]通过试验获取了2A12铝合金Johnson - Cook材料模型的相关参数，其中A=400MPa，B=424MPa，n=0.350，m=1.426，C=0.001，tr=293K，tm=863K。

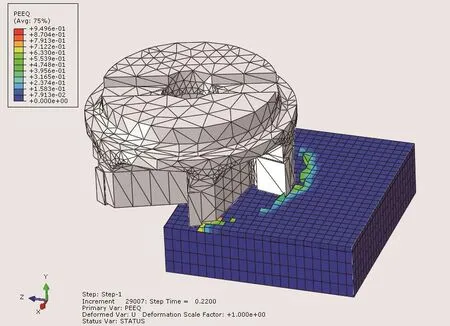
图3 切削仿真过程

图4 仿真切削力曲线

铣削仿真过程如图3所示，通过采集工件对刀具的反作用力，即可获得三方向上的仿真铣削力曲线，如图4所示。仿真结果表明，刀具对工件的铣削力在切向方向上的值为Fx=216N，在进给方向上的值为Fz=-87N，在轴向方向上的切削力为Fy=-72N，铣削合力为：

仿真计算出的铣削力与经验公式计算出的铣削力误差为：

仿真结果与经验公式计算结果接近，可以认为该仿真模型接近真实结果。

2.3 加工变形有限元仿真求解过程

仿真加工工件采用真实尺寸细长导轨模型，导轨的材料为2A12铝合金，长度为4044mm，截面尺寸为290*130mm，最薄处厚度为7mm。加工采样面1、采样面2、采样面3的工装如图5所示。

图5 加工上表面工装

细长导轨通过压板和支撑杆固定在工作台面上，压块和支撑杆在导轨纵向上的尺寸为80mm，在导轨纵向上均匀分布5个图5所示装夹结构。有限元分析过程中，通过对Abaqus进行Python语言的二次开发，可以实现参数化模型求解，简化求解过程。

3 有限元仿真结果分析

3.1 细长导轨截面变形结果分析

细长导轨截面上的加工变形图可以通过一个截面上的所有采样点显示，离端面100mm距离的截面变形图如图6所示。

图6 导轨截面加工变形图

仿真结果表明，导轨采样面1和采样面3虽然结构对称，但由于切削力方向均为x轴正方向、y轴负方向，导致其让刀变形完全不同，因此加工变形也不相同。面1处的加工变形比面3小，因此在实际加工中，应改变面3处的铣削方向，使切削力方向为x轴负方向。同理可在面2上指导铣削的方向。

通过镜像误差补偿理论，我们可以获得刀具的补偿轨迹如图7所示。

图7 导轨截面刀具补偿轨迹图

3.2 细长导轨纵向变形结果分析

细长导轨纵向上的加工变形图可以通过某条采样线上的所有采样点组成，采样面1、采样面2、采样面6上典型采样线加工变形曲线如图8所示。

图8 导轨纵向加工变形图

仿真结果表明，面1的加工表面精度受装夹点位置分布影响较大，变形量最大能达到0.018mm，面2面6在两端的局部刚度较弱，变形量大，中间的变形量小，且面6处的局部刚度比面1和面2强，变形量远小于面1和面2。通过镜像误差补偿理论，面1典型采样线上的刀具补偿轨迹如图9所示。

4 试验验证

图9 导轨纵向刀具补偿轨迹图

为了验证仿真结果的准确性，本文设计了两组加工试验，A组按照装夹方式常规加工，B组通过刀具补偿轨迹对工件进行补偿加工，结果通过三坐标测量仪Daisy564测量。测量过程分为导轨截面尺寸测量和纵向尺寸测量，截面上测量点数量和仿真采样点数量一致，纵向上测量点数量为仿真采样点数量的一半，对仿真出的加工变形曲线、刀具未补偿的加工变形曲线以及刀具补偿后的加工变形曲线进行分析，采样面2上某横截面变形图如图10所示，采样面1纵向典型采样线的变形图如图11所示。

图10 面2横截面变形尺寸对比图

图11 面1纵向典型线变形尺寸对比图

从结果曲线中可以看出仿真出的加工变形曲线和刀具未补偿的实际加工变形测量曲线结果相近，偏差原因是由于加工塑性变形以及残余应力释放导致的。经过刀具路径补偿后的加工变形明显减小，横截面上加工变形量减小约60%，纵向上加工变形量减小约75%，加工变形未完全去除的原因是由于刀具轨迹补偿后铣削力也动态增加，变形量比原有值更大，增加的变形量没有得到补偿所致。

5 结论

1）通过Abaqus铣削过程仿真可以获取真实尺寸的铣刀以实际切削参数加工的三个坐标方向上的铣削力，采用经验公式计算出的铣削力与仿真结果对比，验证了铣削力仿真结果的准确性。

2）通过Abaqus隐式静力学分析代替显示切削过程模拟可以有效减少细长导轨等大型工件的加工变形分析时间，通过Python语音进行二次开发，对大量数据进行了求取与分析，获取了基于真实尺寸工件的加工变形曲线，同时通过镜像误差补偿理论，求取了刀具补偿轨迹。

3）通过试验验证了铣削仿真加工变形模型的准确性，按照刀具补偿轨迹加工，可以明显减少加工变形60%以上，效果显著。

[1] Ratchev S,Liu S,Becker A A.Error compensation strategy in milling flexible thin—wall parts[J].Journal ofMaterials Processing Technology,2005,162(5):673-681.

[2] Weinert K,Grunert S,Kersting M.Analysis of cutting technologies for lightweight frame components in flexible manufacture of lightweight frame structures[J].AdvancedMaterials Research,2006,10:121-132.

[3] 赵欣,欧剑,李跃.薄壁叶片加工变形模型预测与误差补偿[J].制造业自动化,2014,(13):36-40.

[4] 王光宇,吴运新,闫鹏飞,等.航空铝合金薄壁件铣削加工变形的预测模型[J].中南大学学报(自然科学版),2012,43(5):1696-1702.

[5] 王先逵,主编.铣削、锯削加工（机械加工工艺手册:单行本）[M].北京:机械工业出版社,2008.

[6] 尹飞鸿,唐国兴,陈志伟,等.铝合金航空薄壁框铣削变形预测研究[J].制造业自动化,2012,34(9):37-40.

[7] 肖建,林海波.Python编程基础[M].北京:清华大学出版社,2003.

[8] 张伟,魏刚,肖新科.2A12铝合金本构关系和失效模型[J].兵工学报,2013,34(03):276-282.