机加工表面粗糙度的光切显微成像测量方法与试验研究

2016-03-02金守峰田明锐

制造业自动化 2016年4期

金守峰，陈蓉，范荻，田明锐

（1.西安工程大学机电工程学院，西安 710048；2.长安大学道路施工技术与装备教育部重点实验室，西安 710064）

0 引言

机加工零件表面由于在加工过程中的刀痕、切屑分离时的塑性变形、机床设备的高频振动等影响所产生的微小的峰谷称为表面粗糙度。表面粗糙度直接影响产品质量，快速、准确地测量表面粗糙度对于提高产品质量、改善加工条件等均具有重要意义。目前机加工表面粗糙度测量方法有接触式和非接触式测量[1]。接触式测量法即传统的触针扫描法，测量结果稳定可靠，测量灵敏度和横向分辨率较高。测量过程中触针与表面始终保持接触只能对表面进行一维测量，测量效率低。接触式测量尽管对测量力进行了严格控制，但不可避免地会划伤表面和磨损触针。非接触式测量以光学法为主，如光切法、干涉法、散射法和激光法等[2]，光学测量方法对软质表面无损伤，但对光源和测量环境有严格要求，调节光学仪器时人为的主观误差将使测量误差增大，且自动化程度不高，效率低。机器视觉测量技术具有非接触、高精度的优点，不仅可以实现在线测量，而且测量速度快、精度高，是表面粗糙度测量的发展方向。

图像的边缘是图像的基本特征以图像局部不连续的形式出现，表示图像中一个区域的终结和另一个区域的开始。图像的边缘信息包括了目标图像的轮廓信息，常用的经典边缘检测算子有Roberts、Sobel、Prewitt及 Canny算子等，但是这些算子的精度均为像素级，不能满足高精度的边缘检测要求。亚像素边缘检测是通过分解边缘附近的像素来精确定位、细化边缘的方法，常用的算法有形心法、灰度重心法、拟合法和空间矩法等，其中利用矩原理的Zernike典的正交矩分析方法，除了对图像的几何变换具有旋转不变性外，还具有良好的抗噪能力和图像识别能力。

本文利用光切显微镜和CCD成像系统获取零件表面粗糙度的轮廓图像，通过改进Zernike矩方法提取了轮廓的亚像素边界，在此基础上采用最小二乘拟合法确定了轮廓基准中线，根据国家标准建立了轮廓的算术平均偏差Ra的数学模型，实现了机加工表面粗糙度的非接触、高精度测量。

1 光切法测量表面粗糙度系统构成

光切法测量原理如图1所示，光源的光线经狭缝及物镜形成带状光束以45°角的方向投射到被测表面，由于被测表面不是一个理想的光滑反射面，表面具有微小的峰谷，如图1(a)中S点为波峰，S'点为波谷，峰谷点产生反射，分别成像在a与a'点，在目镜中可以看到如图1(b)所示的与被测表面相似的弯曲光带，该光带反映了被测表面的微观几何形状[3]。

图1 光切显微镜的工作原理

由光切显微镜的目镜千分尺测得a至a'点之间的距离h'，而被测表面实际微观不平度峰谷间的高度h为：

式中： h'为45°方向上的成像高度；N为物镜放大倍数。

光切法表面粗糙度测量系统如图2所示。将工业相机1安装在光切显微镜2的相机接口，被测量物3放置在载物台4上，被测物的加工表面经光切显微镜所得到的微观图像经工业相机千兆以太网传输至计算机6，测量系统对图像信号进行预处理、亚像素边缘特征提取、拟合中线，建立粗糙度测量模型自动计算被测物表面粗糙度数值。

图2 光切法表面粗糙度测量系统

2 表面粗糙度轮廓边缘亚像素特征提取

2.1 表面粗糙度轮廓图像预处理

由成像原理可知，光切显微镜的光源是通过狭缝照射在被测表面，而狭缝具有一定的宽度，图像放大后显示的是一条亮带，实际上亮带和背景的上边缘或下边缘即为被测表面微观轮廓，取其一即可。轮廓边缘是图像的基本特征以图像局部不连续的形式出现，表示图像中一个区域的终结和另一个区域的开始。对粗糙度带状图像的边缘特征提取既要将边缘断开连接起来，同时对于远离边缘曲线的像素点剔除掉。在图像采集和传输的过程中，由于受到多种因素影响，往往会导致图像降质[4]。必须对图像进行预处理，以去除噪声干扰、提高图像对比度，增强图像细节信息。预处理后的图像如图3所示，其中图3(a)为原始图像，图3(b)为预处理后的图像，图像边缘特征更加清晰。

2.2 改进Zernike矩的亚像素边缘特征提取

假设单位圆的圆心位于图像的某个像素点上，如果单位圆内存在边缘f(x，y)将该圆分割成两个部分，边缘模型如图4所示。

图4 边缘模型

图4中h为背景灰度，k为阶跃灰度，则阴影部分的灰度值为h+k，l为圆心到边缘的垂直距离，ø为边缘垂直线与x轴的夹角。

边缘f(x，y)的n阶m次Zernike矩定义为：

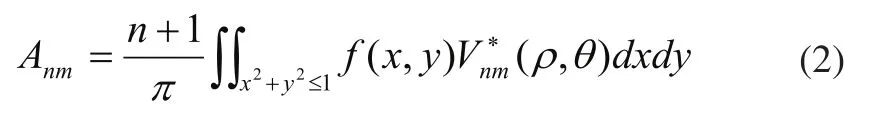
将图像顺时针旋转角度ø，使ø=0，则边缘f(x，y)与y轴平行，如图4(b)所示，旋转后的边缘为f‘(x，y)，则有：

根据Zernike矩定义，式(2)即为相应矩A’11的虚部位为：

图像旋转角度为：

Zernike矩具有旋转不变的特性，即旋转前后Zernike矩只改变相角，而幅值不变。由此可推导出A00、A11、A20所对应的积分核函数为：

旋转后图像的Zernike矩为：

由式(6)、式(7)、式(8)联立可求解其参数为：

假设在边缘检测过程中采用的模板大小为N×N，对放大效应进行修正，得到利用Zernike矩进行亚像素边缘检测的计算公式为：

式中：xi，yi为亚像素坐标值；x，y为原点坐标值。

公式(9)为如图5(a)所示的理想阶跃模型推导出边缘亚像素坐标值，但所获取表面粗糙度轮廓图像的边缘难以达到理想阶跃状态，必然存在如图5(b)所示的过渡区域。

图5 亚像素边缘模型

在传统的Zernike算法中，利用 k≥T ∩ l≤δ作为选取亚像素边缘的判定依据，由于2δ必须小于一个像素的长度，所以δ选取为一个像素长度的1/。由于阶跃灰度k的范围较大，阈值T对边缘的判断结果以及算法的精度有着极大的影响。本文根据过渡区域中图像的灰度值与阶跃灰度值在同一像素点具有相同的变化趋势，以最大类间方差法计算目标与背景基于阶跃灰度的最大类间方差从而得到最优的阈值T。

实际计算过程中，本文利用经典的Sobel算子确定表面粗糙度轮廓图像的像素级边缘，再利用上述改进的Zernike矩对像素级边缘进行亚像素定位，避免对整幅图像进行Zernike矩计算，提高了计算效率。最终获得表面粗糙度轮廓图像亚像素级边缘如图4所示。

3 表面粗糙度计算

3.1 基于图像边缘特征的最小二乘拟合中线

在粗糙度测量中中线是具有几何轮廓形状并划分轮廓的基准线，以此基准线评定表面粗糙度的幅度参数。在表面粗糙度带状图像边缘特征提后，确定其坐标位置，设测量图像的坐标系为x-o-y，表面粗糙度轮廓曲线为f(x)。本文以最小二乘拟合中线作为评定表面粗糙度的基准线，则最小二乘拟合中线的回归方程为：

回归系数分别为：

式中：m为采样点数，xi为采样点x轴坐标，yi为采样点y轴坐标

通过图4所提取的边缘点所对应的位置坐标，以最小二乘法拟合中线如图6所示。

图6 最小二乘中线

最小二乘拟合中线回归方程中为：

表面粗糙度轮廓各点距离最小二乘中线的距离为轮廓偏距Zi：

在取样长度上的轮廓平均偏距为：

3.2 粗糙度评定参数模型

以国标GB/T3505-2009为依据，建立粗糙度评定参数模型。粗糙度评定参数各项参数包括幅度参数和间距参数，按国家标准规定必须标注的幅度参数为轮廓的算术平均偏差Ra，轮廓的算数平均偏差的定义为在一个取样长度内纵坐标值的绝对值的算数平均值，可以充分反映工件表面微观几何形状特征，本文在取样长度范围内建立轮廓算术平均偏差Ra的数学模型为：

式中：za为轮廓平均偏距，K为标定系数。

4 试验分析

4.1 标定

用CCD获取被测零件表面轮廓图像时，边缘信息会以像素为单位转换成数字信号，则被测表面的物点映射到图像平面上像素点，两者的位置之间存在确定的对应关系，要得到被测表面的粗糙度必须确定每个像素所代表的真实物理尺寸，即标定系数。本文使用标准刻度尺进行标定，在不同物镜放大倍数下测量刻度尺图像的像素数N(pixel)，已知刻度尺的尺寸L(μm)，则在幅度方向的标定系数K为：