基于状态空间模型的铸型装配质量预测

杜宝瑞，刘 跃，屈力刚，苏长青

（地址：）

0 引言

砂型铸造方法可用来生产钢、铁和大多数有色合金铸件。由于砂型铸造所用的造型材料价廉易得，铸型制造简便，对铸件的单件生产、成批生产和大量生产均能适应，长期以来，一直是铸造生产中的基本工艺，砂型铸造方法生产出的铸件精度等级低，尤其在尺寸偏差与形状偏差等外观质量方面。而解决这一难题的关键是控制铸型装配质量，在内型芯与外型腔尺寸偏差设计阶段，要根据铸型装配过程建立状态空间模型描述型腔偏差流传递机理，建立模型参数与装配工艺参数的对应关系[1～6]。

状态空间模型是描述和预测多工序加工和装配偏差传递过程的有效方法。HU首先提出偏差流理论，用以分析和预测零件装配过程中的传播机理[7]。AGRAWAL等提出了用于描述多工位装配过程偏差流的回归模型，但这些模型都是基于统计基础的没有定量描述出影响零件尺寸偏差的因素与零件尺寸偏差的关系[8～10]。田兆青等利用状态空间模型，解决了主要针对依靠定位元件保证装配精度的误差流传递机理，如汽车车身、飞机机身等薄壁件装配过程，这些装配误差主要来自夹具本身[11]。LIU等将偏差描述扩展到三维空间构建了刚体零件的三维偏差传递过程状态空间模型，但仍主要将定位元件偏差作为误差来源[12～15]。红军等对加工误差导致的关键特征方位偏差进行数学建模，确定偏差源表达。针对精密机床装配过程，构建状态空间模型并建立模型参数与装配工艺参数的对应关系。然而这些研究主要针对串联式装配过程，最后需要保证装配质量部位是有限的[16]。而对于像铸型装配这样的工艺来说需要保证装配质量的部位是一个封闭的腔体，连续的实体，是无数个连续的部位，并且装配部件间成阵列分布[17]。

铸型装配误差来源主要是由于内型芯与外型腔基础大件特征面的尺寸公差在装配过程中形成体间误差，为保证封闭腔体尺寸公差，解决这一类型尺寸偏差积累问题就需要研究加工误差导致的配合特征变化引起的体间误差表达，建立基于状态空间模型的空间实体尺寸链，定量描述封闭腔体尺寸公差模型。构建铸型调整与测量工艺的状态空间模型，为铸型装配精度预测、偏差溯源，装配工艺优化等奠定基础[18～20]。

本文提出了将铸型装配质量预测工艺进行数学表达，运用状态空间模型对影响铸型装配质量的关键指标进行描述与定量表达。首先构建描述装配部件特征的坐标系，对装配部件的关键几何特征、参考坐标系以及由于砂芯和砂箱公差引起的砂芯关键特征位姿的变化进行数学表达，确定装配过程偏差流传播机理及偏差流的定量表达。其次建立基于状态空间模型的空间实体尺寸链的数学模型定量描述封闭腔体尺寸公差，构建模型参数与装配工艺参数的对应关系，定量描述阵列式装配的铸型装配质量。最后通过某航空铸件生产工艺为例，证明该方法的有效性。

1 装配体在状态空间模型中的描述

装配体在状态空间模型中设定如下假设：参与装配的砂芯及砂箱为刚体。

通过四种坐标系对装配过程中关键几何特征进行描述，坐标系O0表示参考坐标系,用来确定装配过程中每个部件及特征相对于基准参考的位置和姿态，同时也可看成整机装配过程中的测量基准。特征坐标系Ok位于部件定位特征理想位置几何中心处，表征部件的理想位置和姿态。部件实际坐标系位于部件定位特征实际位置几何中心处，表征部件的实际位置和姿态。 如图1所示。

图1 描述装配过程各部件坐标系变换关系

空间中个部件最多有6个自由度，即三个平动自由度X、Y、Z和三个转动自由度α、β、γ。在装配过程中，其中由三个平动自由度引起的坐标变换可由平移坐标变换表达，三个转动自由度引起的坐标变换可由横滚（roll）、俯仰(pitch)和偏转(yaw)旋转集合表达。各坐标系空间位姿变换可由平动和旋转集合的齐次变换来表达，齐次变换矩阵为：

其中T为特征表面相对于理想表面的变换矩阵，RPY3×3为旋转矩阵，P3×1为平移矢量。

1.1 理想条件砂芯的坐标变换

理想条件下多工位装配中，各部件坐标系相对于参考坐标系进行坐标系转换，旋转变换矩阵由横滚、俯仰和偏转，按“从右向左”依次相乘原则进行运算（右乘）

装配体中砂芯的理想坐标系与参考坐标系二者之间对应关系如下：

式中x、y、z和α、β、γ分别表示Zk部件理想坐标系相对于参考坐标系的位置和姿态变化。cα、cβ、cγ分别代表cosα、cosβ、cosγ，sα、sβ、sγ分别代表sinα、sinβ、sinγ。

1.2 误差引起的砂芯坐标系变换

在每一工位实际装配过程中，由于砂芯和砂箱尺寸公差引起装配体中部件坐标系变换。

1）当砂芯的尺寸公差及装配偏差相对于砂芯及砂箱基本尺寸来说很小。部件理想位置坐标系和实际位置坐标系可以通过以下其次坐标变换表示二者之间的对应关系。

式中，Δα ,Δ β , Δγ和 Δ x,Δ y,Δz分别为Zk部件实际坐标系相对于理想坐标系的位置和姿态变化。

2）当偏转角度与弧度不在一个数量级时

式中α、β、γ和x、y、z分别表示Zk部件实际坐标系相对于理想坐标系的位置和姿态变化。cα、cβ、cγ分别代表cosα、cosβ、cosγ，sα、sβ、sγ分别代表sinα、sinβ、sinγ。

2 误差流的传递与表达

砂芯装配误差流传递的状态空间模型设定如下假设：

1）参与装配的砂芯及砂箱为刚体。

2）部件在竖直方向上移动误差为零。

3）参考部件的偏差角度近似等于弧度。

4）误差流主要由砂箱定位特征尺寸公差引起。

5）由装配体砂芯表面形位公差因素引起铸件壁厚误差归结为砂箱定位特征尺寸公差引起。

在理想状态下砂芯边界点的数学模型为：

式中Ak为描述砂芯侧表面点的行矩阵，Rk为理想砂芯几何特征的半径。

在实际装配中由于砂芯形位误差引起的砂芯表面特征变换：

椭圆的一般式为：

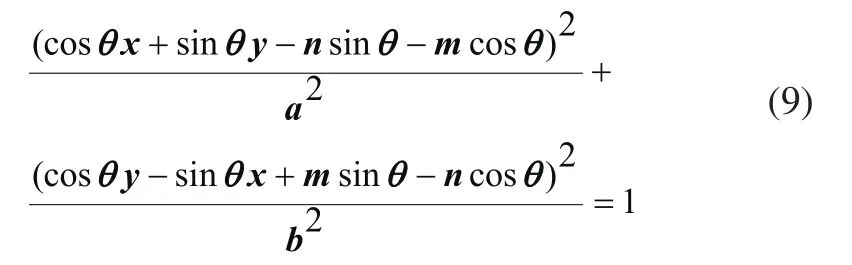
其中a,b分别为长短轴，θ为椭圆对称轴相对于坐标系的偏转角度，（m,n）为椭圆中心坐标。(8)-(9)对应相等可知6个约束得到5个参数。当ΔT满足式(4)时有：

可知6个约束中有一个是虚约束得到参考部件表面特征点集参数如下：

其中ak、bk、mk、nk、θk分别为参考部件的长短轴、中心坐标和斜椭圆偏转角度。

2.3 用型腔厚度尺寸公差反应装配质量

变换具有封闭性，建立空间实体尺寸链如图2所示。

图2 空间尺寸链

将图2截面放在平面坐标系建立相应数学模型

如图3所示方程1，方程2的方程如式(8)所示，方程3直线方程为过(m0,n0)斜角为θ的方程：

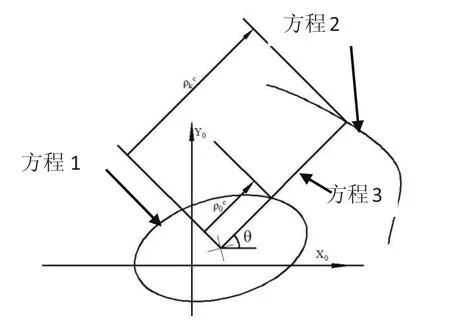
图3 二维空间尺寸链

分别联立参考部件方程1与直线方程3，装配部件Zk的方程2与直线方程3得到与Z0部件的交点Z0(x0,y0)与Zk部件的交点Zk(xk,yk)。

如图2所示封闭空间为型腔的公差区间，描述型腔尺寸公差的数学模型为：

在现有的装配精度等级下，型腔尺寸公差是关于θ,z的函数，可利用二分法寻求尺寸超差区域，进行装配质量预测。

2.4 用砂芯几何特征方向和位置偏差反映装配质量

如图3所示，在空间建立角度尺寸链，其中参考部件的坐标系相对于参考系的偏转角度为Δ1θ，部件理想坐标系相对参考坐标系偏转角度为θ，部件实际坐标系现对于理想坐标系的偏转角度为Δ2θ，部件实际坐标系相对于参考部件坐标系的偏转角度为封闭角度尺寸用Δθ表示。

在图3中，沿着坐标轴方向各偏角逆时针为正，顺时针为负。

描述部件方向偏差的数学模型为：

图4 角度尺寸链

描述部件偏移距离偏差的数学模型为：

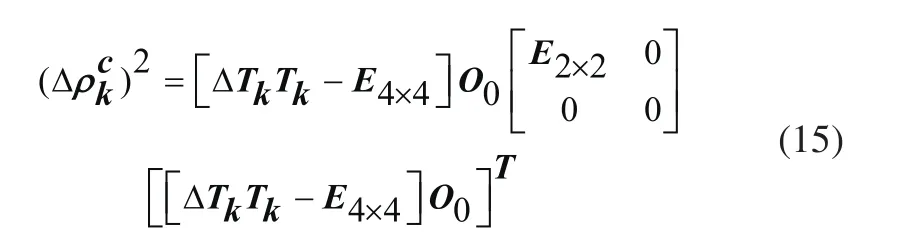
3 应用实例

3.1 案例描述

本案例描述了某航空铸件砂型的装配过程，用此砂型铸造生产HB6103CT9级的某航空铸件，并利用状态空间模型描述其装配过程中偏差流传递的解析形式，最后依据关键特征分析铸型装配质量。

如图4所示，在本道工位中需要装配的部件有装配体Zi（i=1,2,3,4)，参考部件Z0在第一道工位中完成装配，具体装配的位置关系如图5所示。

图5 铸型装配示意图

表1 部件定位几何中心极坐标及特征尺寸 mm

在部件实际装配过程中沿着Z轴移动对装配质量影响很小，可以忽略不计，根据现有装配质量等级，确定各部件位姿偏差如表2所示。

表2 各部件尺寸偏差引起的装配偏差 mm

3.2 累积偏差计算及装配质量分析

以Z1部件为例，计算部件Z1与参考部件Z0形成封闭腔体的空间尺寸公差，部件Z1的偏转角度Δθ以及偏移理想位置半径。

实际装配中，根据各装配体装配误差敏感方向，应用极大值法预测封闭腔体尺寸公差，Z0绕x、y的旋转角度为分别为0.80°，沿着x、y的移动距离为20.0mm。部件Z1、Z3为-5.62°，移动距离-30.5mm、40.3mm。Z2、Z4为-2.54°移动距离-20.0mm、-23.5mm.

根据部件Z1的装配误差等级可知ΔT1满足式(4)，由式(7)

根据式(8)得：

方程1：

方程2：

根据式(9)～式(11)可得到参考部件斜椭圆的中心为(0.80 z +20,-0 .80 z-20)

方程3为：

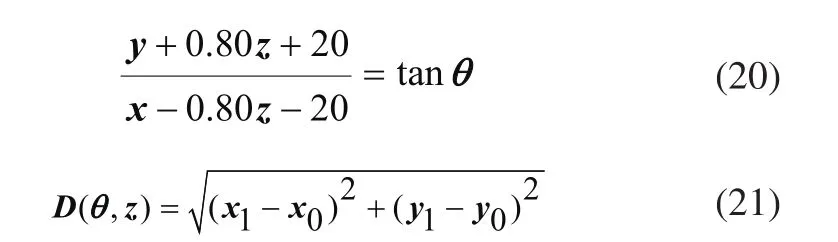
根据式子(14)，可得到部件Z1偏转角度尺寸链。

根据公式(15)可得到特征部件偏移半径为：

4 结论

1）利用空间状态模型，描述偏差流的传递与转换过程，建立起描述多部件阵列装配的空间误差流传递与转换的数学模型。

2）利用空间尺寸链，过滤误差流，减少对装配质量无影响或影响少的误差流，建立影响装配质量的误差流的空间体尺寸链。

3）提出了装配预测结果的评定方法和关键特征偏差的表达方法，建立起设计公差与装配质量的对应关系。

4）通过某航空铸件的砂型装配为实例，验证该算法的有效性。

[1] 洪军,郭俊康,刘志刚,武晓攀.基于状态空间模型的精密机床装配精度预测与整工艺[J].机械工程学报,2013.49(6):114-115.

[2] PAIREL,E.,HERNANDEZ,P.,GIORDANO,M.,Virtual Gauge Representation for Geometric Tolerances in CAD-CAM Systems[J].Journal of Design and Manufacturing,Springer,The Netherlands,2007:5-6.

[3] FARMER,L.E.,GLADMAN,C.A.,Tolerance Technology-Computer Based Analysis of the CIRP[M],1986,Vol.35,Part 1:7-10.

[4] Ramesh V.Narang.An Innovative Approach of Team-Teaching Measurement Uncertainty and Metrology[J].Midwest Section Conference of the American Society for Engineering Education.2007:1-2.

[5] 田兆青,来新民,林忠钦.多工位薄板装配偏差流传递的状态空间模型[J].机械工程学报,2007(02):202.

[6] Cheng Y.Lin,Nathan J.luetke.Calculation of Tolerance Stacks Using Direct Position Approach in Geometric Dimensioning ang Tolerancing[J].Journal of engineering Technology.spring2011.

[7] J.E.Freckleton. Production Advantages of GD&T and inseparable Assemblies[J].Journal of Mechanical Working Technology,17(1988):237-248.

[8] 刘玉生.基于数学定义的平面尺寸公差数学模型[J].机械工程学报,2001,09:13.

[9] 张马彪,叶晓平,刘玉生.基于自由度变动的直线尺寸公差数学模型[J].工程设计学报,2009(6):173.

[10] 蔡自兴.机器人学基础[M].王璐2009年6月第一版第一次印刷.机械工业出版社.2009.5:15-26.

[11] PAIREL,E.,The gauge model:A new approach for coordinate measurement[J].Proceedings of the XIVIMEKO World Congress, Tampere,Finland,1997:278-280.

[12] N.C.梭罗宁.装配尺寸链和工艺尺寸链的计算[M].1986年1月第1版.上海科学技术文献出版社.1986.1.1:18-22.

[13] ETESAMI,F.,Position Tolerance Verification Using Simulated Gaging[J].The International Journal of Robotics Research,1991,Vol.10,No.4:358-360.

[14] Verification of Geometric Tolerances With the”Fitting Gauge”Model[M].ASME-Journal of information Science in Engineer NO.1:28-30.

[15] 李弘英,赵成志.铸造工艺设计[M].余茂祚2005年3月第一版.机械工业出版社.2005.3:11-15.