带落角约束的空地导弹智能滑模末制导律研究*

刘成亮,辛腾达,周兴旺,肖冲华

(1 空军航空大学,长春 130022;2 装备学院,北京 101416;3 沈空装备部,沈阳 110000)

带落角约束的空地导弹智能滑模末制导律研究*

刘成亮1,辛腾达2,周兴旺1,肖冲华3

(1 空军航空大学,长春 130022;2 装备学院,北京 101416;3 沈空装备部,沈阳 110000)

为了提高空地导弹的打击效能,追求最佳的毁伤效果，文中在解耦后的空地导弹目标相对运动模型的基础上,应用基于零化视线角速率的准平行接近原理及滑模变结构控制理论设计了带落角约束的空地导弹滑模末制导律。应用模糊控制理论与RBF神经网络理论,分别对滑模趋近系数与切换项增益系数进行自适应调节。最后,对文中所设计的末制导律进行仿真验证,仿真结果表明该末制导律能够以期望的落角命中目标,具有一定的理论参考价值。

空地导弹;落角;滑模控制;模糊控制;RBF神经网络

0 引言

现代战争对于空地导弹的制导能力及打击效果提出了越来越高的要求,仅将命中目标作为空地导弹的最终制导目的已经远远不能满足现代战场的实际需求。因此,为了有效的发挥空地导弹的战斗效能,还需要对空地导弹末制导中的落角等进行相应的约束[1]。因此,文中针对空地导弹的末制导问题,设计了一种带落角约束的空地导弹智能滑模末制导律。

滑模变结构控制由于对外界的干扰及参数的变化具有强鲁棒性,引起了国内外研究人员的广泛关注,为带落角约束的空地导弹末制导律的设计提供了良好的理论基础[2-3]。Byung与Jang等人应用滑模控制理论设计了一种修正比例制导律,该制导律在打击目标的过程中能够导引导弹以期望的落角命中目标[4]。20世纪90年代起,周荻等人开创了国内滑模制导律研究的先河。但其主要的研究工作集中在二维平面内[5]。吴鹏等人设计了一种对脱靶量和末端攻击角度同时进行约束的滑模制导律,然而未对系统的抖振问题进行充分的考虑[6-7]。李士勇等人将滑模控制理论与智能控制理论相结合,但其未对相应的落角约束问题进行研究[8-9]。周德云针对空空导弹、防空导弹带攻击角度约束的制导律的研究[10-11],刘通在带落角约束的穿甲弹制导律的研究[12],秦元岗对侵彻弹多约束制导律的研究[13],雷炜针对反舰导弹带终端角度制导律的研究都取得了长足的进步[14]。他们的工作为带落角约束的滑模制导律的研究提供了良好的基础和依据。

1 空地导弹目标相对运动模型

合适的数学模型是进行问题研究的重要前提,不同的研究对象、不同的设计需求,所建立的模型及其优化方法也不同。文中为方便空地导弹末滑模末制导律的设计,首先根据需求对空间内空地导弹-目标相对运动模型进行解耦研究。

1.1 空地导弹-目标相对运动模型解耦

文中在空间内空地导弹-目标相对运动模型为基础,忽略空地导弹的滚转运动的影响,在视线坐标系下,将空地导弹-目标的相对运动解耦成俯仰平面和偏航平面内的运动,如图1所示。

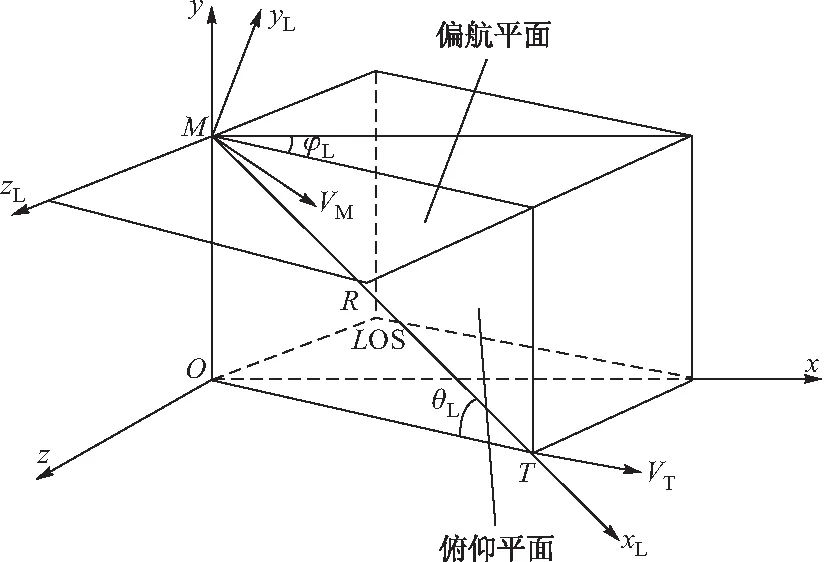
图1 弹-目俯仰平面和偏航平面示意图

图1中:M为空地导弹初始点,T为目标点,LOS为空地导弹-目标视线,VM与VT分别为空地导弹及目标的速度矢量,θL为视线倾角,φL为空视线偏角,R为视线距离。

俯仰平面定义为M点、T点及O点所确定的平面,即My、MyL、MxL所确定的平面;偏航平面定义为过M点且平行于xOz的平面,即MzL、Mz′、Mx′所确定的平面,Mz′过M点与Mz平行,Mx′过M点与Mx平行。因此,空地导弹末制导律可以在俯仰平面和偏航平面内分别进行设计。文中以偏航平面内带落角约束的空地导弹智能滑模末制导律的设计为例,俯仰平面内采用相同的方法进行设计。

偏航平面内的空地导弹-目标相对运动模型,如图2所示。

图2 偏航平面内弹-目相对运动关系

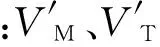
对图2所示的偏航平面内空地导弹-目标相对运动关系进行分析,可得:

(1)

1.2 空地导弹末制导律落角约束分析

(2)

(3)

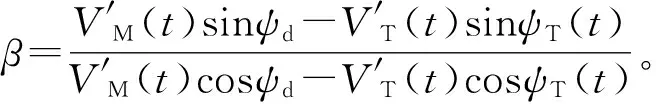
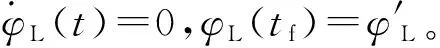
2 带落角约束的滑模末制导律设计

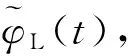
(4)

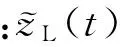
(5)

对式(5)进行微分:

(6)

(7)

(8)

式中:

(9)

式中:aMφ(t)、aTφ(t)分别为导弹与目标垂直于LOS的加速度。

则式(8)可表示为:

(10)

令:

(11)

(12)

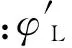
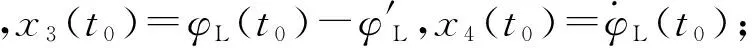
终端条件:t=tf时,x3(tf)=0,x4(tf)=0。

对式(11)、式(12)进行求导变换,并且与式(10)进行联立,可得:

(13)

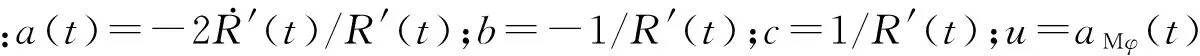
(14)

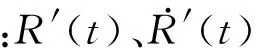
空地导弹在末制导过程中具有高度的时变性特征。因此,文中采用具有一定自适应能力的指数趋近律形式:

(15)

式中:k>0为趋近律系数,ε>0为切换项增益系数,sgn(S)为切换项。

文中利用Lyapunov判稳方法来判断系统的稳定性,取能量函数为V=S2/2>0,对其进行求导变换可得:

(16)

对式(14)进行求导,可得:

(17)

(18)

可得:

(19)

联立式(14)、式(15)、式(19)可得:

(20)

式中:aTφ为目标机动加速度,若aTφ≠0,即表明目标进行机动。aTφ在空地导弹末制导中是不能够准确得到的,我们将aTφ视为干扰量,在末制导的过程中aTφ为有限的,即满足:

|aTφ(t)|≤f

(21)

将aTφ视为外部干扰,滑模末制导律对外部环境干扰具有鲁棒性。因此,aTφ对滑模末制导律的制导性能不产生影响,则式(20)可表示为:

(22)

所求得的aMφ为偏航平面内空地导弹指令加速度,即偏航平面内带落角约束的滑模末制导律。

3 智能滑模末制导律研究

随着计算机技术的高速发展,智能控制理论在不确定、非线性控制系统中发挥了重要作用。文中应用模糊控制理论与RBF神经网络理论分别对滑模末制导律的趋近律系数k与切换项增益ε进行智能自适应调节。

3.1 趋近律系数的模糊自适应调节

趋近律系数k决定着末制导律的大小及变化速率,影响着末制导律的鲁棒性与抖振特性。传统滑模制导律大多根据以往的设计经验将k设定为常值,这无疑影响了系统的鲁棒性且易引起抖振[15]。因此,文中应用模糊控制理论对k进行调整,在不影响滑模末制导律鲁棒性的前提下,有效的提高其制导性能。

趋近律系数项k的取值范围通常在范围2～6内,文中根据导弹末制导律趋近律系数调节的需要,输入的范围取为(-6,6),用以下七个变量作为模糊控制输入语言变量:

{负大 负中 负小 零 正小 正中 正大}

英文缩写表示为:

{NB NM NS ZE PS PM PB}

作为模糊控制输入的语言变量;

因为趋近律系数式中为正值,选择VS、MS、M、LM、VL作为模糊控制输出的语言变量。其中,VS为极小、MS为中小、M为中、LM为中大、VL为极大。

根据空地导弹制导的一般经验可知,当滑模状态量较大时,为了能够提高视线角速率的收敛速率,使系统快速的到达S=0,应具有较大的控制量;当系统滑模状态量趋近于零时,应具有较小的控制量,保证制导系统的稳定性与收敛性。因此,文中设计的模糊控制规则,如表1所示。

文中所设计的模糊推理系统为2输入1输出系统,有49条模糊规则,选用三角形隶属函数、Mamdani推理构成模糊推理系统,如图3所示。

表1 模糊控制规则表

图3 模糊推理系统的构成

文中所设计模糊推理系统的输入输出曲面,如图4所示。

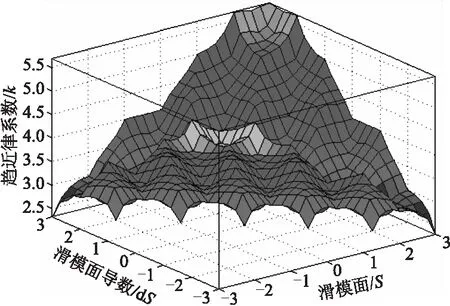
图4 模糊推理系统的输出曲面

3.2 切换项增益系数的RBF神经网络智能调节

切换项增益系数ε主要是用来抵消系统参数变化及外界干扰的影响,不仅影响着系统状态的切换速度,也影响着系统的收敛速度,决定着制导律的动态性能。在实际的应用中ε是很难确定的,ε选的过小,无法抵消外界干扰的影响,不能满足到达条件的要求;ε选的过大,又会造成系统严重的抖振。因此,文中应用RBF神经网络对ε进行实时在线智能调节,优化滑模末制导律的动态性能。

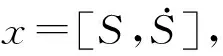
ε=|wTh(x)|

(23)

式中:w为RBF神经网络的权值;h(x)为高斯函数。

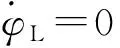
(24)

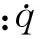
(25)

(26)

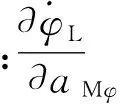
由式(22)可得:

(27)

由式(23)可得:

(28)

故式(26)可写成:

(29)

则w的学习算法为:

w(k)=w(k-1)+Δw(k)+δ(w(k)-w(k-1))

(30)

应用式(30)对w进行实时在线调整。空地导弹末制导过程具有高度实时性,为了简化设计,缩短学习时间,文中将高斯函数的基宽B、中心点C固定为常值,文中取文中RBF神经网络系统隐含层的高斯函数,如图5、图6所示

(31)

B=

(32)

图5 隐含层S高斯函数

图6 隐含层dS高斯函数

4 仿真验证

为了验证所研究滑模末制导律的制导性能,应用Matlab对文中所设计的智能滑模末制导律进行仿真验证[16-17]。将仿真步长均设为T=1 ms,RBF神经网络的学习速率η=0.6,惯性系数δ为0.05,网络的初始权值均取为w=[1 1 1 1 1 1 1 1 1 1 1]。

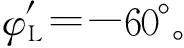
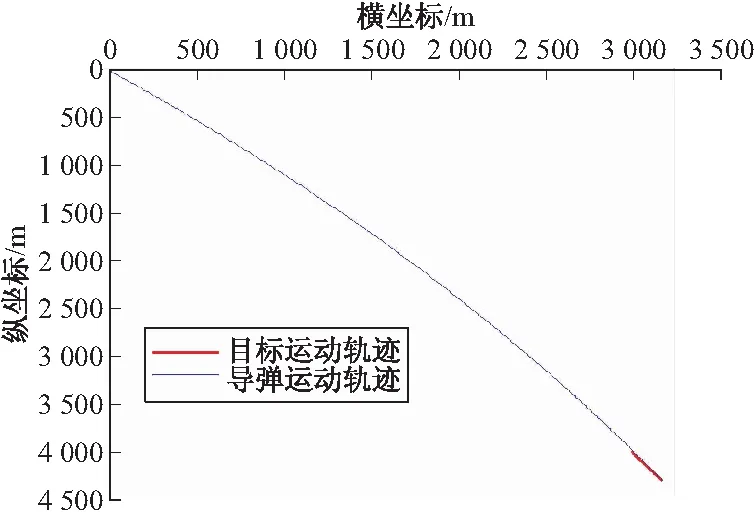
图7 空地导弹-目标运动轨迹

图8 空地导弹-目标相对距离

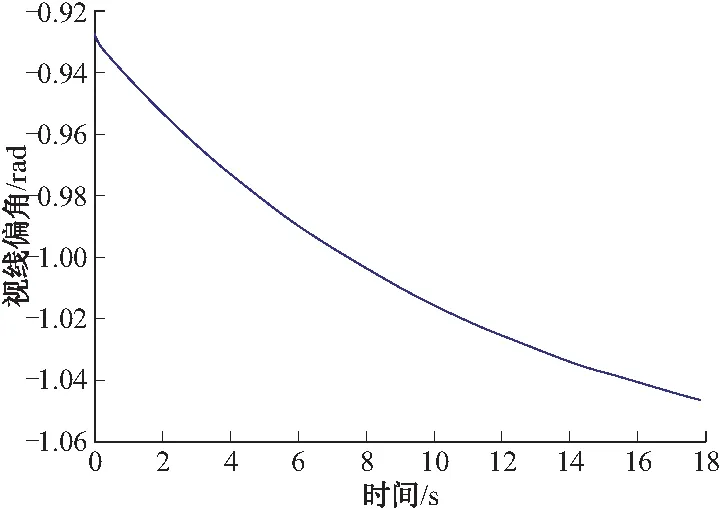
图9 空地导弹-目标视线偏角

5 结束语

文中针对空地导弹末制导的问题,以解耦后偏航平面内空地导弹-目标相对运动模型为基础,设计了带落角约束的空地导弹滑模末制导律,并利用模糊控制理论与RBF神经网络理论分别对滑模末制导律的趋近律系数与切换项增益系数行了智能自适应调节。经过Matlab仿真验证表明,所设计的带落角约束的空地导弹智能滑模末制导律能以期望的落角命中目标,满足空地导弹末制导律对落角约束的要求。

[1] 孙未蒙. 空地制导武器多约束条件下的制导律设计 [D]. 长沙：国防科学技术大学, 2009: 3-10.

[2] QIN Tian, CHEN Wan-chun, XING Xiao-lan. A method for precision missile guidance with impact attitude angle constraint [J]. Joural of Astronautics, 2012, 33(5): 570-576.

[3] 陈志梅, 王贞艳, 张井岗. 滑模变结构控制理论及应用 [M]. 北京: 电子工业出版社, 2012: 1-13.

[4] KIM Byung Soo, LEE Jang Gyu. Homing guidance with terminal angular constraint against nonmaneuvering and maneuvering target:AIAA 97-3474 [R]. 1997.

[5] ZHOU Di, MU Chun-di, LING Qiang, et al. Study of optimal sliding-mode guidance law [J]. Chinese Juournal of Aeronautics, 1999, 12(4): 236-241.

[6] 吴鹏, 杨明. 带终端攻击角度约束的变结构制导律 [J]. 固体火箭技术, 2008, 31(2): 116-120.

[7] 吴鹏. 带末端攻击角度约束的制导方法研究 [D]. 哈尔滨: 哈尔滨工业大学, 2009: 33-56.

[8] 李士勇, 章钱. 智能制导: 寻的导弹智能自适应导引律 [M]. 哈尔滨: 哈尔滨工业大学出版社, 2011: 138-146.

[9] 章钱, 李士勇. 一种新型自适应RBF神经网络滑模制导律 [J]. 智能系统学报, 2009, 4(4): 339-344.

[10] 杨峰, 周德云, 张堃, 等. 具有终端约束的制导炸弹模糊变结构制导律设计 [J]. 指挥控制与仿真, 2013, 35(1): 131-134.

[11] 卢春燕, 周德云, 张堃, 等. 基于RBF的带落角约束的最优滑模导引律设计 [J]. 电光与控制, 2012, 19(5): 20-22.

[12] 刘通, 潘涛, 杨军, 等. 反装甲车导弹落角约束制导律研究 [J]. 战术导弹技术, 2013(6): 91-96.

[13] 秦元岗. 带末端多约束的航空侵彻炸弹制导律研究 [D]. 长沙: 国防科学技术大学, 2010: 89-105.

[14] 雷炜. 反舰导弹具有末端碰撞角约束的末制导方法研究 [D]. 哈尔滨: 哈尔滨工业大学，2012: 40-42.

[15] 周荻. 寻的导弹新型导引规律 [M]. 北京: 国防工业出版社, 2002: 47-50.

[16] 刘金琨. RBF神经网络自适应控制MATLAB仿真 [M]. 北京: 清华大学出版社, 2014: 45-56.

[17] 刘金琨. 滑模变结构控制MATLAB仿真 [M]. 2版. 北京: 清华大学出版社, 2012: 324-346.

Research on Intelligent Sliding Mode Terminal Guidance Law for Air-to-ground Missile with Impact Angle

LIU Chengliang1,XIN Tengda2,ZHOU Xingwang1,XIAO Chonghua3

(1 Aviation University of Air Force, Changchun 130022, China; 2 Academy of Equipment, Beijing 101416, China; 3 Shenyang Air Force Armament Division, Shenyang 110000, China)

In order to improve the guidance property of the Air-to-ground missile, and achieve the best efficiency of damage. An intelligent sliding mode terminal guidance law for Air-to-ground missile with impact angle was designed based on the decoupled Air-to-ground missile and target relative motion model, the theory of zeroing the rate of line-of-sight angular rate and the sliding mode variable structure control theory. The fuzzy theory was used to adaptive adjust the reaching coefficient, and the RBF neural network was used to adaptive adjust the switching term gain coefficient. Finally, the designed terminal guidance law was verified by simulation, and the simulation results show that the terminal guidance law can hit the target with the expected impact angle, and has a certain theoretical reference value.

air-to-ground missile; impact angle; sliding mode control; fuzzy control; RBF neural network

2015-05-19

刘成亮(1984-),男,吉林辽源人,讲师,硕士,研究方向:制导武器使用与仿真。

TJ765.3

A