温度变化时抗拉刚度对结构位移和内力的影响

刘晓红（宁夏建设职业技术学院,银川 750021）

温度变化时抗拉刚度对结构位移和内力的影响

刘晓红
（宁夏建设职业技术学院,银川 750021）

用结构力学求解器计算杆系结构在荷载作用下的内力和位移时，一般不考虑杆件的轴向变形，即把抗拉刚度EA设为无穷大。论文用结构力学求解器，求解二次超静定结构在温度变化时不同数量级的抗拉刚度产生的内力和位移的大小，进而对其大小进行比较和研究，得出温度变化时需要考虑杆件的轴向变形的结论。

温度变化；抗拉刚度；结构力学求解器；内力和位移

【DOI】10.13616/j.cnki.gcjsysj.2016.12.007

1 引言

目前,多层和小高层住宅大多采用框架结构。框架结构分析时，在荷载作用下不考虑梁的轴向变形通常是可行的，就是说在设置单元材料性质时可以将抗拉刚度EA设为无穷大，而柱子轴力通常很大其变形是要考虑的，即EA不能设为无穷大。除此之外，众多实验和研究表明温度变化和支座沉降时杆件的轴向变形也需要考虑[1,2]。

结构力学求解器[3]是清华大学研制的一款简单实用的计算机辅助计算软件，可以分析求解二维平面结构（体系）的几何组成、静定结构的内力计算、超静定结构在荷载和温度变化以及支座沉降时的内力和位移计算、影响线、自由振动、弹性稳定、极限荷载[4]等，并都能给出精确解答。本文就是利用结构力学求解器的精确计算功能[5，6]，求解超静定结构在温度变化及抗拉刚度EA取不同数值时的不同位移和内力值，以此研究比较得出结论，即温度变化时不能忽略杆件轴向变形，否则会给结果带来很大误差。

2 外侧温度变化时超静定结构的结构力学求解器分析模型

简单的二次超静定结构如图1所示。图中（1）、（2）为单元编号，其下数字为单元长度，单位为m；t=17.5和t=32.5为内外侧温度，单位为℃；1,2,3为杆端号。杆件的抗弯刚度EI=120000kN·m2,抗拉刚度EA为变化值，其单位为kN。

在软件中输入的INP文件如下：

结点,1,0,0

结点,2,0,4

结点,3,-4,4

单元,1,2,1,1,1,1,1,1

单元,2,3,1,1,1,1,1,1

结点支承,3,2,-90,0,0

结点支承,1,6,0,0,0,0

单元温度改变,1,2,25,15,0.00001, 0.5

单元材料性质,1,2,5e6,1.2e5,0,0,-1

图1 二次超静定结构模型

3 外侧温度变化时超静定结构的位移

不同抗压刚度下结构的位移值比较见图2。

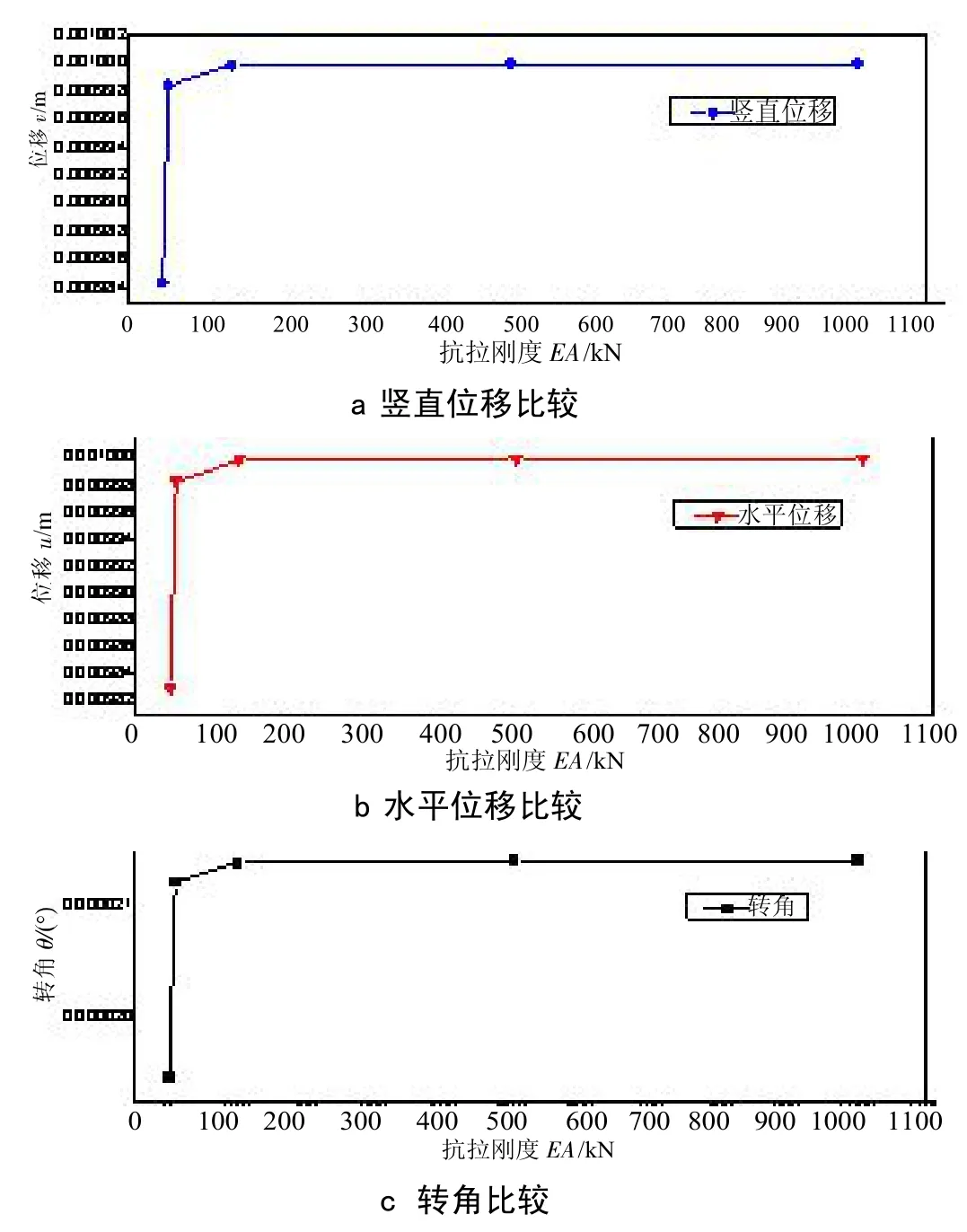
图2 不同抗拉刚度下结构的位移值比较

表1 杆端位移值表

根据图2和表1的数据进行分析：

由于单元（1）杆端2处的位移与单元（2）杆端1处的位移相同，所以整个结构以2结点的位移为研究对象，对其水平位移u、竖直位移v、转角θ进行分析：

1)取结构抗拉刚度EA=5×104与EA=5×105时的位移比较：

2)取结构抗拉刚度EA=5×105与EA=5×106时位移比较：

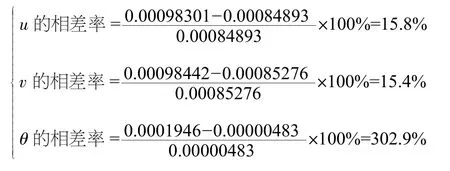
(3)结构抗拉刚度EA=5×107与EA=∞时位移比较:

通过以上分析可以得出结论：

EA=5×107与EA=∞比较后的水平位移u、竖直位移v、转角θ相差率都远远小于5%（工程允许范围）。这说明在计算位移时，如果杆件本身抗拉刚度足够大，是可以不考虑轴向变形的，而抗拉刚度分别取5×104，5×105，5×106时其水平位移、竖直位移以及转角相差率远远超过5%，甚至EA=5×104时的竖直位移和转角的方向与其他抗拉刚度下的方向都是相反的。另外，图2中不论是转角、水平位移还是竖直位移，都是在EA=5×108以后折线才开始趋于平缓，这说明温度变化时计算位移需要考虑轴向变形，就是说不能简单地将抗拉刚度EA设为无穷大。本文所选模型只是简单的二次超静定结构，倘若是实际工程中的框架结构、框架剪力墙结构等更为复杂的超静定结构，在温度变化时计算位移都是要考虑轴向变形的。

4 外侧温度变化时超静定结构的内力

不同抗拉刚度下结构内力值比较见图3。

图3 不同抗拉刚度下结构的内力值比较

图中选取了EA分别为5×106,5×107,5×108,2.5×109,5×109的5个数值，求解出剪力、轴力、弯矩的比较。为了使横坐标EA的数值看起来简洁，EA的每个数值都在原来数值的基础上除以5×106。

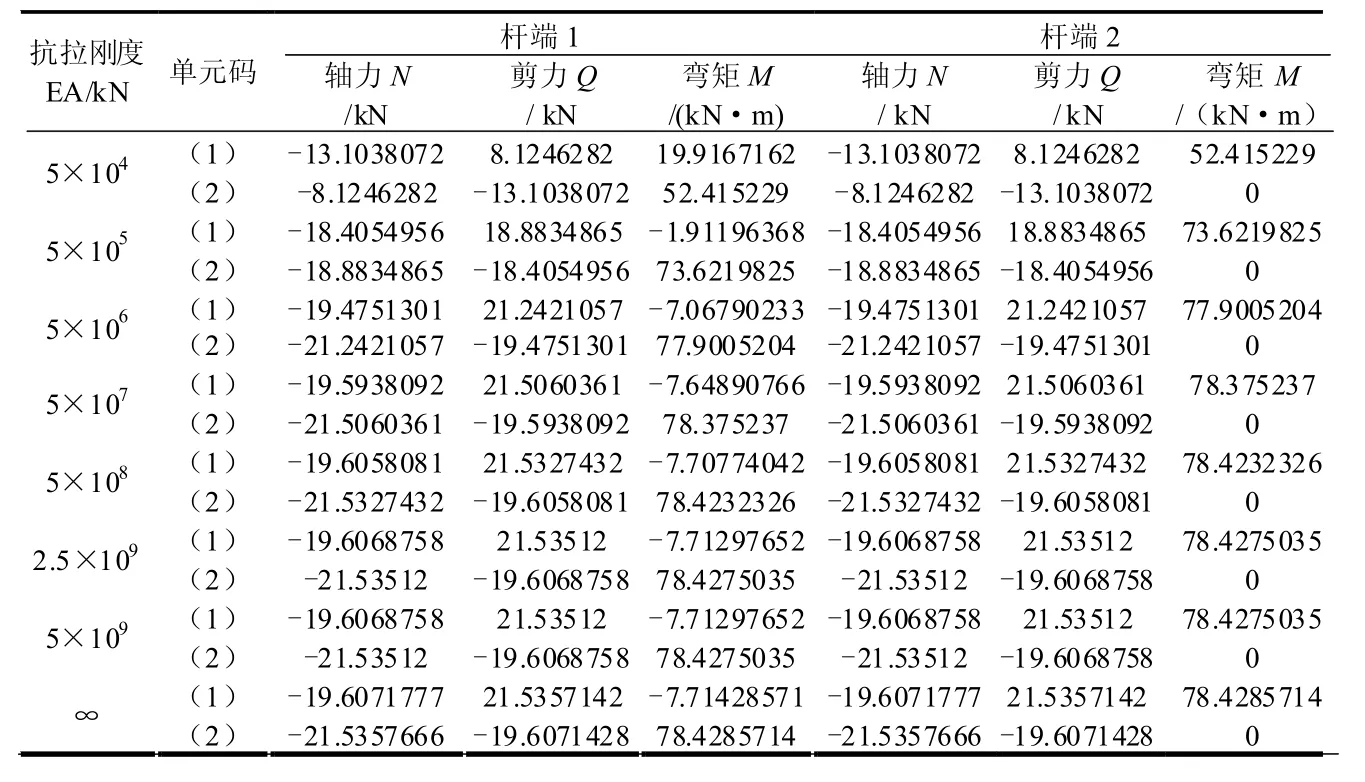
表2 杆端内力值表

根据图3和表2的数据进行分析：

结构以单元（2）杆端1为研究对象，对其轴力N，剪力Q，弯矩M进行分析：

(1)取结构抗拉刚度EA=5×104与EA=5×105时内力比较：

(2)取结构抗拉刚度EA=5×105与EA=5×106时内力比较：

(3)取结构抗拉刚度EA=5×107与EA=∞时内力比较:

通过以上分析可以得出结论：EA=5×107与EA=∞比较后的轴力，剪力Q，弯矩M相差率都远远小于5%（工程允许范围）。这说明在计算杆件内力时，如果杆件本身抗拉刚度足够大，是可以不考虑轴向变形的；而抗拉刚度分别取5×104与5×105比较时其轴力、剪力、弯矩相差率远远超过5%，5×105与5×106比较相差也超过了5%。另外，图3中不论是剪力、轴力还是弯矩都是在EA=5× 108以后折线才开始趋于平缓，这说明温度变化时计算内力需要考虑轴向变形，就是说不能简单地将抗拉刚度EA设为无穷大。本文所选模型只是简单的二次超静定结构，倘若是实际工程中的框架结构、框架剪力墙结构等更为复杂的超静定结构，在温度变化时计算内力都是要考虑轴向变形的。

【1】李国强，王震.一种考虑温度影响的高效几何非线性梁-柱单元[J].同济大学学报（自然科学版）,2016,44（6）：815-821+829.

【2】薛明琛.高层框架弯曲变形引起的侧移与轴向变形引起的侧移间的关系[J].四川建筑,2012,32(1):129-130.

【3】龙驭球,包世华，匡文起，等.结构力学Ⅰ—基本教程[M].北京：高等教育出版社,2012.

【4】袁驷，叶康生，袁征.《结构力学求解器》的算法与性能[J].工程力学，2001（S）:174-181.

【5】刘卫然，张丽梅.结构力学求解器在桁架结构教学中的应用[J].山西建筑,2014,40（11）：276-278.

【6】张秀丽，高志飞.结构力学求解器在钢屋架设计中的应用[J].安徽建筑,2013(4):159-161.

Effect of TensileStiffnessonStructural Displacement and InternalForcewith

LIUXiao-hong
(NingxiaConstructionVocationalandTechnicalCollege,Yinchuan750021,China)

In general, the axial deformation ofmember bar structures does not be consideredwhen internal force and displacementunder the loadwith SMsolver is caculated , that is, theEAis set to infinity. In this paper, SMsolver is used to caculate the internal forceand displacement of secondary statically indeterminate structure of different tensile stiffness with temperature change, and thenthrough comparison we come to the conclusion that the axial deformation of member bars should be considered with temperaturechange.

temperature change; tensile stiffness;SMsolver; internal force anddisplacement

TU311.4

A

1007-9467（2016）12-0043-03

2016-09-09

刘晓红（1987～），女，山东威海人，助教，从事建筑结构设计与研究。