C55 混凝土弹性模量时变应对连续刚构桥的影响研究

顾卫国（南通市交通建设咨询监理有限公司，江苏 南通 226000）

C55 混凝土弹性模量时变应对连续刚构桥的影响研究

顾卫国
（南通市交通建设咨询监理有限公司，江苏 南通 226000）

混凝土材料弹性模量及其时变效应，对于悬臂浇筑预应力混凝土连续刚构桥的施工控制分析至关重要。论文主要通过统计标准养护条件下的混凝土早期弹模和28d弹模值，并通过3～90d内同条件养护下弹模试验的验证，确定C55混凝土弹性模量的时变规律。通过模型验算，可以验证在施工及设计阶段考虑弹模的时变规律，对桥梁可靠设计与安全施工具有重要科学意义和工程价值。

1 前言

在连续刚构的预应力钢筋混凝土梁张拉时，混凝土的强度和弹性模量值均为主要的材料控制指标[1～3]。特别是在张拉C50以上等级高强度预应力钢筋混凝土梁时，更应规定张拉时混凝土应达到的弹性模量值。在预应力张拉后，桥梁的起拱变形与梁体内应力与混凝土弹性模量的变化密切相关，对于连续刚构桥的施工控制及成桥后的全桥受力性能至关重要[4]，因而在对梁各浇筑段混凝土施加预应力时需限定混凝土强度和弹性模量最低值。

在2015年的调研[5]中发现，江苏省连续刚构桥中，已运营桥梁主梁的混凝土等级主要是C50，在建桥梁主梁混凝土等级则主要是C55。因此，本文选取C55混凝土，用于研究混凝土的弹性模量的时变规律对江苏省未来的连续刚构桥施工的影响。

2 不同养护条件下的混凝土弹性模量试验

2.1 标准养护C55混凝土早期弹性模量试验

[6]，本次试验在南通市某特大连续刚构桥采用标准养护试件进行C55混凝土弹性模量试验并得到了四个龄期，共135项弹性模量数据，各龄期下的弹性模量试验结果如表1。

本文结合数理统计相关知识来计算混凝土的弹性模量推定值：

1）自由度小于10时，弹性模量推定值选择最小弹性模量值[7]。

2）自由度大于等于10时，弹性模量推定值选择“95置信区间下界”为该龄期下混凝土弹性模量推定值。其中，自由度大于等于10且小于30时，按 （式1）计算95置信区间下界；自由度大于等于30时，按 （式2）计算95置信区间下界[8]。

标准养护条件3～7d内弹性模量推定值如表2所示。

其中，龄期为5d的弹性模量试验值，存在两个异常值（大于），在数据处理过程中已被剔除（剔除异常值前数据方差为0.1201，剔除异常值后方差为0.0743，其数据的离散性在剔除异常值后趋于稳定）。从表2可以看出，4～7d内混凝土弹性模量基本符合规范要求。

2.2 标准养护C55混凝土弹性模量28d弹性模量研究

本次试验依托南通某连续刚构桥，按文献[9]的标养要求，在2014年5月1日采用标准养护（试验条件21℃/51%）试件进行C55混凝土弹性模量试验并得到共158项弹性模量数据（×104MPa）：4.14，4.20，4.38，4.24，4.13，4.14，4.39，4.50，4.39，4.26，4.26，4.21，4.33，4.37，4.06，4.38，4.31，4.13，4.28，4.46，4.22，4.20，4.26，4.26，4.35，4.31，4.29，4.20，4.38，4.38，4.29，4.34，4.53，4.30，4.45，4.11，4.04，3.97，4.27，4.26，4.11，4.54，4.38，4.45，4.20，4.11，4.46，4.53，4.50，4.17，4.09，4.25，4.51，4.18，4.47，4.23，4.37，4.27，4.28，4.18，4.53，4.42，4.04，4.43，4.26，4.42，4.11，4.54，4.20，4.22，4.38，4.26，4.25，4.16，4.18，4.26，4.35，4.21，4.22，4.20，3.92，4.34，4.25，4.30，4.38，4.34，4.46，4.18，4.26，4.31，4.15，4.22，4.20，4.22，4.20，4.40，4.30，3.91，4.34，4.46，4.11，4.04，4.27，4.63，4.14，4.13，4.30，4.13，3.99，4.33，4.67，4.27，4.06，4.10，4.17，4.45，4.10，4.35，4.25，3.92，4.06，4.02，4.41，4.45，4.26，4.43，4.25，4.04，4.60，4.24，4.52，4.18，4.22，4.13，4.06，4.33，4.38， 4.00，4.36，4.05，4.31，4.24，4.10，4.43，4.25，4.30，4.26，4.20，4.54，4.40，4.34，4.36，4.24，4.16，4.53，3.98，4.18，4.59 。

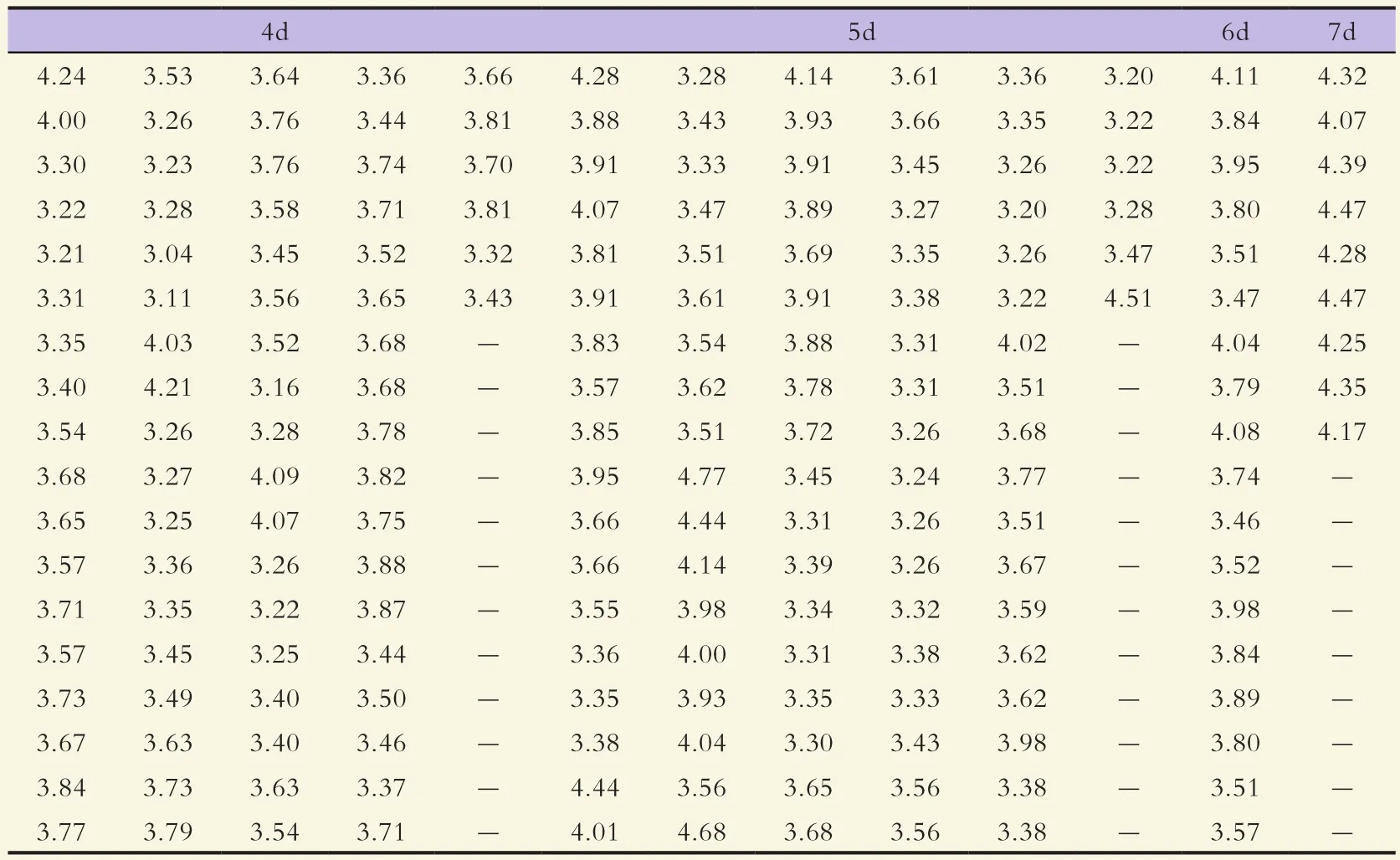
表1 标准养护条件3～7d内弹性模量试验值表 4×10MPa

表2 标准养护条件3～7d内弹性模量试验值表

表 3 标准养护条件下C55混凝土的 28d弹性模量计算项目和计算结果

通过数理统计的方法，取95置信区间下界为标准养护条件下C55混凝土的28d弹性模量。计算项目和端及L/4的变形情况，若要较为准确的掌握结构在不同施工阶段的挠度变化，应当在模型计算时考虑混凝土弹性模量的时变效应对结构挠度的影响。

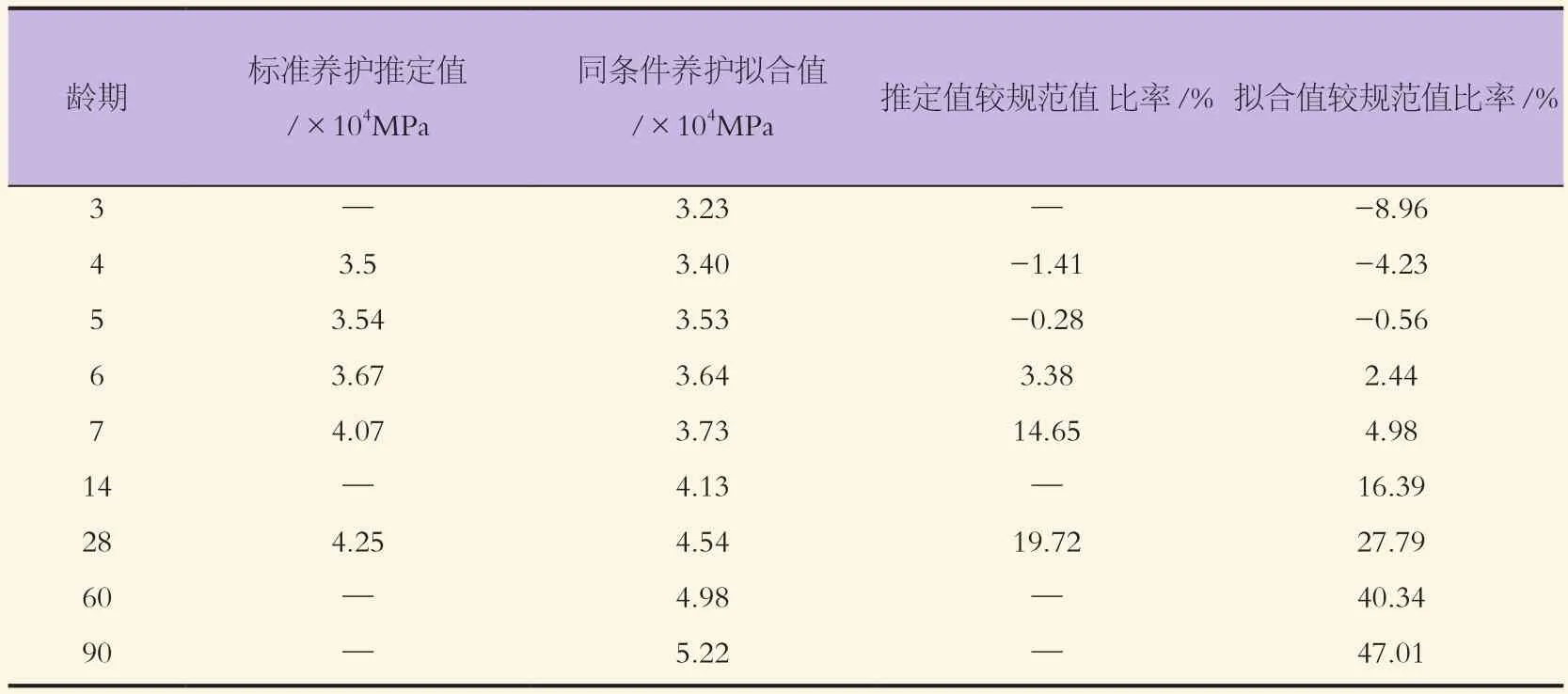
表6 不同养护、不同龄期C55混凝土弹性模量值

表7 弹性模量时变效应对结构的挠度影响

4 结论与建议

混凝土的弹性模量作为衡量混凝土刚度大小的指标，其数值与组成混凝土材料的特性、混凝土的配合比及龄期有关。

第一、C55混凝土在标准养护条件及同条件养护条件下，其28d弹性模量值均超过C55混凝土弹性模量规范值19.72%和19.72%，后期混凝土弹性模量仍有较大程度提高。因此，在混凝土连续刚构设计阶段，关于C55混凝土的弹性模量的模型参数，可以适当提高20%，为4.26× 104MPa。

第二、在施工阶段模型计算时，若要较为准确的掌握结构在不同施工阶段的挠度变化，应当在模型计算时考虑混凝土弹性模量的时变效应对结构挠度的影响。

参考文献

[1]刘尚,文翠翠. 高性能混凝土弹性模量试验研究［J］. 商品混凝土,2009（04）:36-37.

[2]张竞男,胡晓波,鲍光玉,王志. 粉煤灰高性能混凝土弹性模量的试验研究［J］. 混凝土,2003（11）:42-44.

[3]曹茂柏. 对混凝土弹性模量影响因素的探讨［J］.科技通报,2012（12）:195-197.

[4]赵顺波,高宇甲,陈记豪等. C50泵送混凝土抗压强度和弹性模量时变性试验研究与应用［J］. 混凝土,2015（01）:98-101.

[5]张柳煜.陕西省连续刚构桥梁调查报告［R］.西安：长安大学.

[6]张劲泉,王文涛.桥梁检测与加固手册［R］.北京:人民交通出版社,2006.

[7]张建仁,王海臣,杨伟军. 混凝土早期抗压强度和弹性模量的试验研究［J］. 中外公路,2003（03）:89-92.

[8]李俊成,李祖辉,彭亦博等. 混凝土标准养护室的设计与施工［J］. 混凝土与水泥制品,2012（11）:74-76.

[9]汪荣鑫, 数理统计［M］. 西安：西安交通大学出版社,1986.

[10]陈邦玉,王帮,周金森. 混凝土同条件养护试块强度与结构实体强度的相关性研究［J］. 浙江建筑,2005（05）:18-19.

[11]林星平. 混凝土弹性模量及徐变度的计算［J］.云南水力发电,1999（04）:15-18.

[12]丁晗. 高墩大跨连续刚构桥施工监控中的标高及线形监测研究［D］.西安:长安大学,2010.

顾卫国（1972～），男，江苏南通人，高级工程师，从事市政公用工程、公路桥梁工程、水运工程监理研究。（电子邮箱）464890660@qq.com。

The elastic modulus and time-varying effect of concrete material are very important to the construction analysis of concrete continuous rigid frame bridge. This paper calculated the time-varying effect of C55 to determine the elastic modulus of concrete mainly through statistical early concrete elastic modulus and 28d elastic modulus values in the standard curing conditions and the 3d～90d elastic modulus values in the same curing condition. Through the model analysis, the time-varying effect of elastic modulus in the construction and design stage is great scientific significance and engineering value for the reliable design and safety construction of continuous rigid frame bridge.

连续刚构；弹性模量；时变效应；早期弹模

Continuous rigid frame bridge; Modulus of elasticity; Time-varying effect; Early age elastic modulus