加锚复合土钉支护体系可靠度分析与实证

王　辉，杨向前，郜新军

(1.河南理工大学土木工程学院， 河南焦作454003；2.周口市规划建筑勘测设计院， 河南周口466000； 3.郑州大学土木工程学院， 河南郑州450001)



加锚复合土钉支护体系可靠度分析与实证

王辉1，杨向前2，郜新军3

(1.河南理工大学土木工程学院， 河南焦作454003；2.周口市规划建筑勘测设计院， 河南周口466000； 3.郑州大学土木工程学院， 河南郑州450001)

摘要：为对加锚复合土钉支护体系的可靠度进行分析与论证，在分析可靠性原理的基础上，从土钉加固机理出发，假定滑移面为圆弧线，对复合支护体系的外部稳定性进行分析；假定滑移面为改进的双折线，对复合支护体系的内部稳定性进行分析；结合工程实例，通过二阶距法对内外部的极限状态功能函数进行可靠度分析。分析与实证结果表明：将可靠度指标用于预应力锚杆复合土钉支护体系的稳定性分析，可以考虑土体的变异性和不确定性，克服了传统的极限平衡理论的弊端；改进的双折线破裂面用于分析复合支护体系的内部稳定性，可考虑土钉支护上部受拉、下部受剪的受力特征，简单合理。研究结果可以为该类工程设计提供较好的理论基础与计算依据。

关键词：复合土钉；预应力锚杆；可靠度；稳定性分析；滑移面

0引言

预应力锚杆复合土钉支护体系由土钉、预应力锚杆及加固土体等组成，其中土钉与预应力锚杆分属不同工作机制的支护构件，土钉以基坑边壁土体的水平侧移为代价产生轴力，对土体提供约束；而预应力锚杆通过预应力施加限制土体位移。施工过程中锚杆预应力的施加在自由段范围内产生压应力区，导致位于该区的上层土钉的轴向拉应力显著降低，优势滑裂面位置发生迁移，并可能限制下层土钉约束作用的发挥。特别是在外界不利因素的影响下，整体上安全可靠的复合支护体系在施工过程中存在着失稳的可能性。对于这类主被动复合支护体系的稳定性分析，以往的研究成果主要侧重于极限平衡分析。计算时将土体视为具有“平均”性质的“均质”材料，土体参数恒定，荷载与计算方法确定，所有未知的、不确定性的因素归结到单一的安全系数K中。但由于岩土介质实际上具有高度的变异性和不确定性，且计算模型的可行与否及工作环境的变化均包含许多不确定性。因此，极限平衡分析这种定值法尽管易于接受，但存在一定的理论缺陷。近年来，一些学者将结构工程中的可靠度理论引入到支护体系的稳定性分析中，比如：黄广龙等[1]考虑岩土参数的不确定性及变异性，通过对土性参数进行空间折减实现可靠度分析；罗晓辉等[2]在分析土性参数变异的基础上进行了土钉支护体系的可靠度分析；苏倩[3]通过研究锚杆的破坏形式，建立单根锚杆破坏的功能函数，计算支护体系整体稳定的可靠度指标。目前的研究成果大多基于单一的土钉或锚杆支护体系的可靠度进行分析[4-11]，对于加锚复合土钉这种复杂支护形式的研究较为少见。本文在分析可靠性原理的基础上，拟从土钉加固机理出发，对加锚复合土钉支护体系的外部稳定性进行分析；假定滑移面为改进的双折线，建立复合土钉支护体系的内部稳定分析模型，并根据建议的可靠指标，采用二阶距法对内外部的极限状态功能函数进行可靠度分析。

1可靠性分析原理

影响预应力锚杆复合土钉支护体系稳定性的因素多而复杂，某些影响因素无法定量描述，难以确定其准确的概率分布，传统的定值方法无法求解。二阶距模型将抗力系数、荷载效应按照假定的概率估算可靠指标或失稳概率，仅以均值和标准差作为控制参数对计算表达式进行线性处理[12]。目前应用较为广泛的是验算点法，基本原理如下：

基坑工程中，破坏概率Pf可用抗力R与下滑力F表达如下：

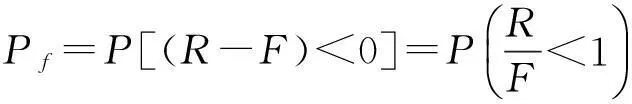
(1)

相应地，安全储备的表达式为：

Z=R-F。

(2)

当Z>0时，偏于安全；当Z<0，倾于破坏。此时状态函数的均值μZ可用标准差σZ度量，即：μZ=βσZ。其中，β为可靠指标，定义为均值μZ与标准差σZ的比值，推导过程如下：

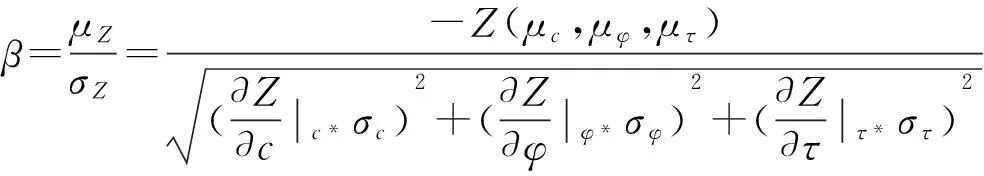
(3)

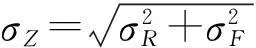
2复合支护体系的外部稳定性分析

2.1土钉加固机理

表观形式上，土钉支护体系与锚杆支挡体系及加筋土结构较为相似，但从作用机理上分析，三者各有特点。锚杆支挡体系为传统的支护方式，采用“荷载—结构”的模式设计，锚杆作为整个支护体系的支点，将作用于支护体系上的侧向水土压力通过锚杆的自由段及锚固段传递到深层土体，实现支挡的目的，属于“锚固机制”，如图1所示。加筋土结构的施工过程与土钉支护体系完全相反，通常从下往上分层填筑，填料可以随机选择，密度与强度可以自由控制，底部的位移较大，相应地下部受力较大，属于“加固机制”，如图2所示。

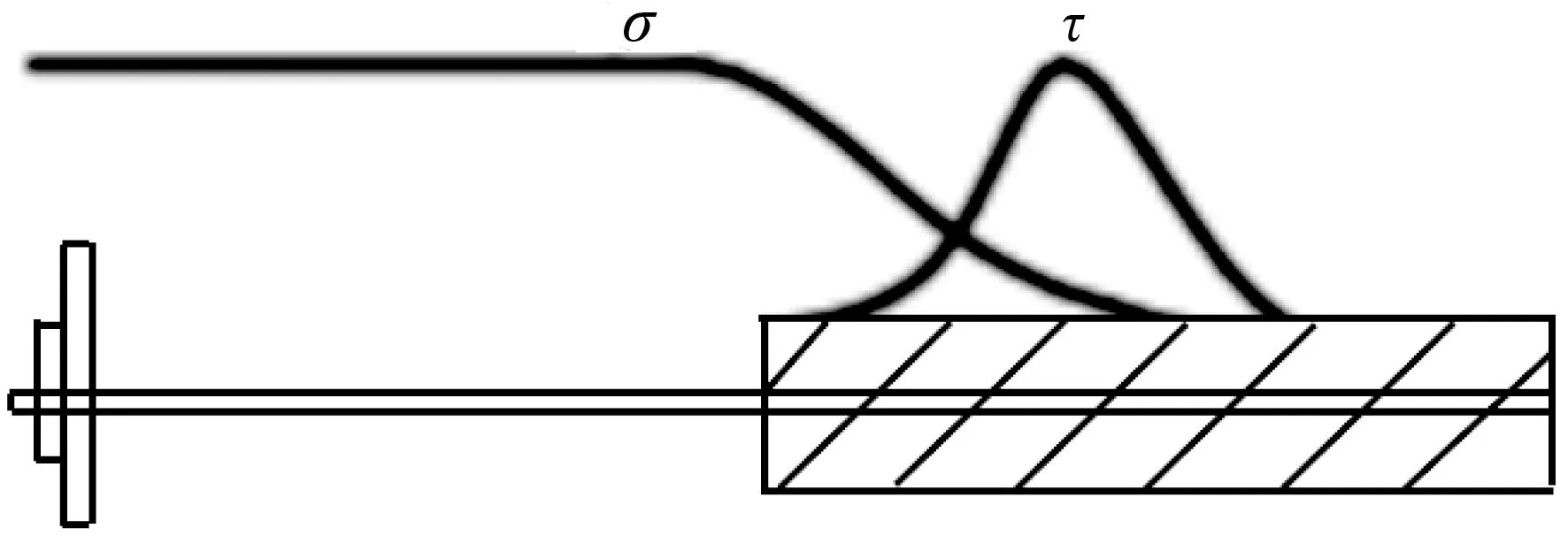
图1预应力锚杆的内力分布

Fig.1Stress distribution of pre-stressed anchor

图2加筋土结构的变形分布

Fig.2Deformation distribution of

reinforced earth structure

而土钉支护体系，由“支护结构与岩土体共同作用”的现代支护理论发展而来，施工时在原位土体中植入钢筋并注浆，在基坑边坡中形成钉土复合体，通过水泥砂浆在土体中的渗透，提高原有土体的力学强度，限制边坡的变形，从而保持基坑的稳定，属于“加固机制上的锚固机制”。

根据前述分析，土钉支护体系可以充分利用原有土体的力学强度，使其成为支护体系的一部分。而且根据已有研究成果[13]，预应力锚杆复合土钉支护体系中，锚杆施加预应力只能改变土钉内力的大小，对土钉内力的分布及传递特征几乎没有影响，与土钉墙基本相同；土钉几乎不对锚杆产生影响，锚杆仍然表现出其固有的特性。因此，在对预应力锚杆复合土钉支护体系进行外部稳定性分析时，可将土钉加固视为一种土体改良，即认为经过加筋的土体形成了类重力式挡土墙。

图3　复合土钉外部稳定分析图示Fig.3　Diagram on external stability ofcomposite soil-nailed retaining structure

参照《建筑地基基础设计规范》(GB50007-2011)规定的重力式挡土墙稳定性的验算方法，进行外部稳定性分析时分别需要验算墙底抗滑性、墙体抗倾覆性及深层土体抗滑稳定性。而土钉墙外部稳定性的优化分析表明：土钉墙的深层土体抗滑稳定性较墙底抗滑及墙体抗倾覆稳定性差[14]。这是因为，一般情况下，土钉墙较厚，基底面较宽，可提供较大的抗滑力与抗倾覆力。因此，外部稳定性分析时仅需验算土钉墙的深层土体抗滑稳定性。

验算时可采用瑞典条分法，假定滑裂面为圆弧形，圆心为O，土条宽度均为b。因土钉墙视为一个被加固的整体，外部稳定性分析时不再考虑土钉的作用。受力分析见图3所示。

取第i个土条进行分析，考虑锚杆的锚固作用，得下滑力F、抗滑力R分别为：

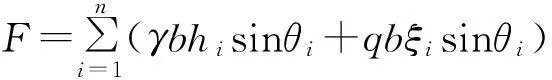
(4)

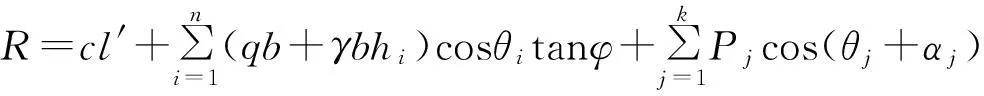
(5)

式中，l′表示整个圆弧长度，m；b表示平均每个土条宽度，m；n为土条总数；k为锚杆排数；θi表示第i土条与水平面夹角，(°)；θj表示第j根锚杆处滑移面与水平面夹角，(°)；αj表示第j根锚杆与水平面的夹角;hi表示第i土条的平均高度；ξi表示第i土条的地面超载系数，若有，取1，若无，取0。

则有，安全储备Z=R-F为：

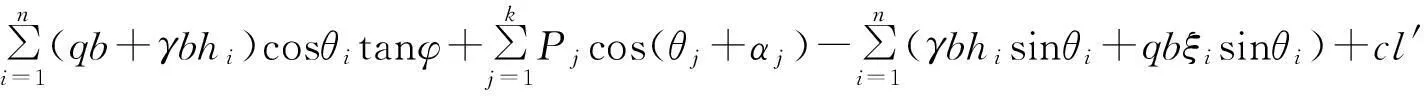
(6)

令Z=0，将式(6)转化为关于x的方程，将Z分别对c,tanφ,τ求导，可得：

(7)

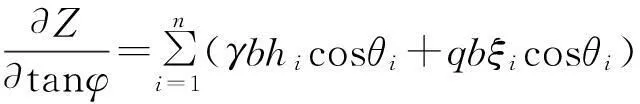
(8)

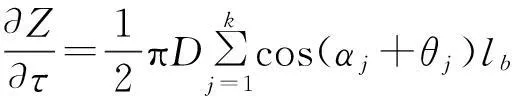
(9)

将式(7)～(9)代入式(3)，即可求出复合支护体系的外部稳定可靠指标。

3复合支护体系的内部稳定性分析

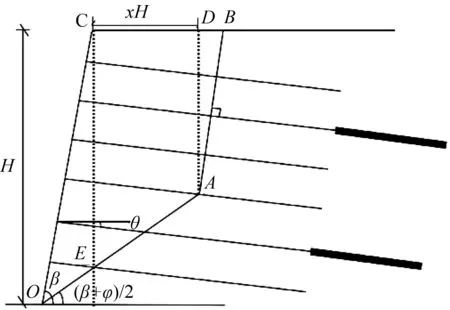
图4　复合土钉内部稳定分析图示Fig.4　Diagram on internal stability ofcomposite soil-nailed retaining structure

进行内部稳定性分析时，本文选用考虑土钉支护结构上部受拉、下部受剪的拉裂—滑移双折线型滑裂面。认为土钉支护结构的滑裂面通过坡脚。对于滑裂面与地面的交点，通常采用试算的方法，不同的滑裂面对应不同的安全系数，最小安全系数对应的即为最危险滑移面的位置。基本假定如下：

①假定滑动土体为刚性体；

②假定土钉拉力在拉裂面及滑移面处同时达到最大值，且该处剪应力为零，两侧剪应力方向相反；

③假定拉裂面为一直线，且与土钉轴向垂直，滑移面为一直线，通过坡脚；

④不考虑预应力施加对土钉墙应力场的影响。

受力分析见图4所示。

如图4所示，坡面倾角为β，拉裂面AB与土钉轴向垂直，滑移面OA穿过坡脚，与水平面夹角为(β+φ)/2，基坑高度为H，CD为xH，通过试算法得到。由图4中几何关系，可得：

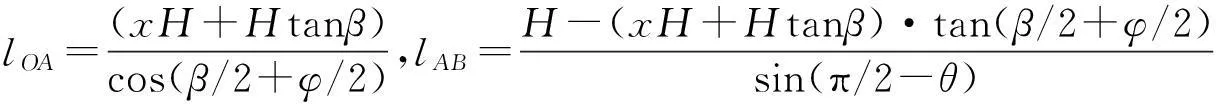
则下滑力F，抗滑力R分别为：

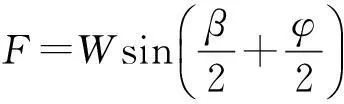
(10)

(11)

其中，

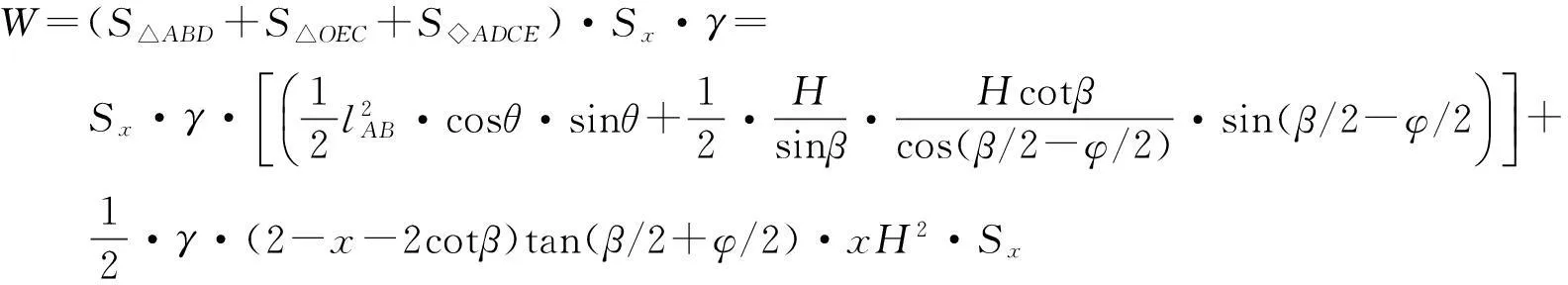
(12)

式(12)中，Sx表示土钉(锚杆)水平间距，m；Ti表示第i根土钉的抗拔力，kPa，按滑裂面外的钉土黏结力计算,Ti=πDnloiτ；Pj表示第j根锚杆的抗拔力，kPa，按锚固段的钉土黏结力计算,Pj=πDalbjτ；τ为钉土界面黏结强度，kPa。

则有，安全储备Z=R-F为：

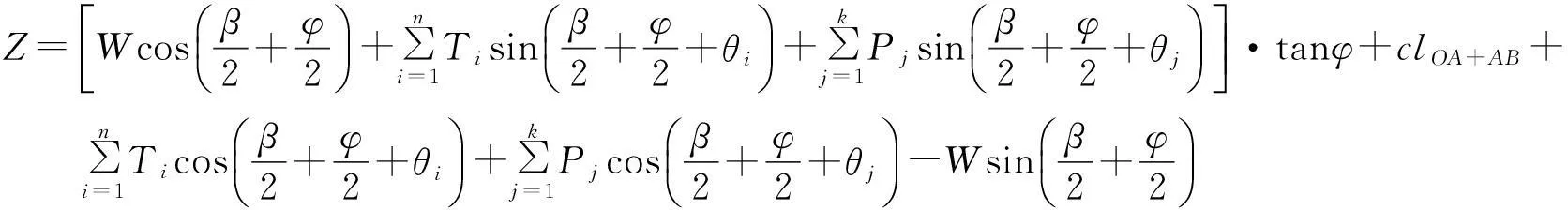
(13)

可得：

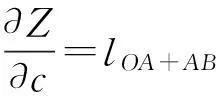
(14)

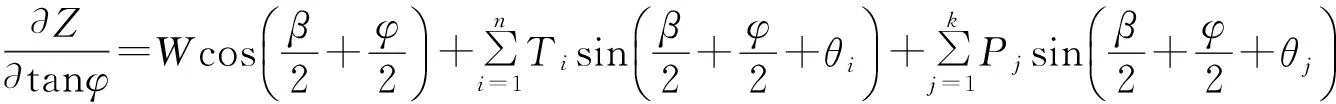
(15)

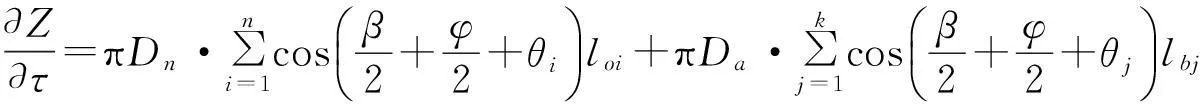
(16)

将式(16)～(18)代入式(3)，即可求出复合支护体系的内部稳定可靠指标。

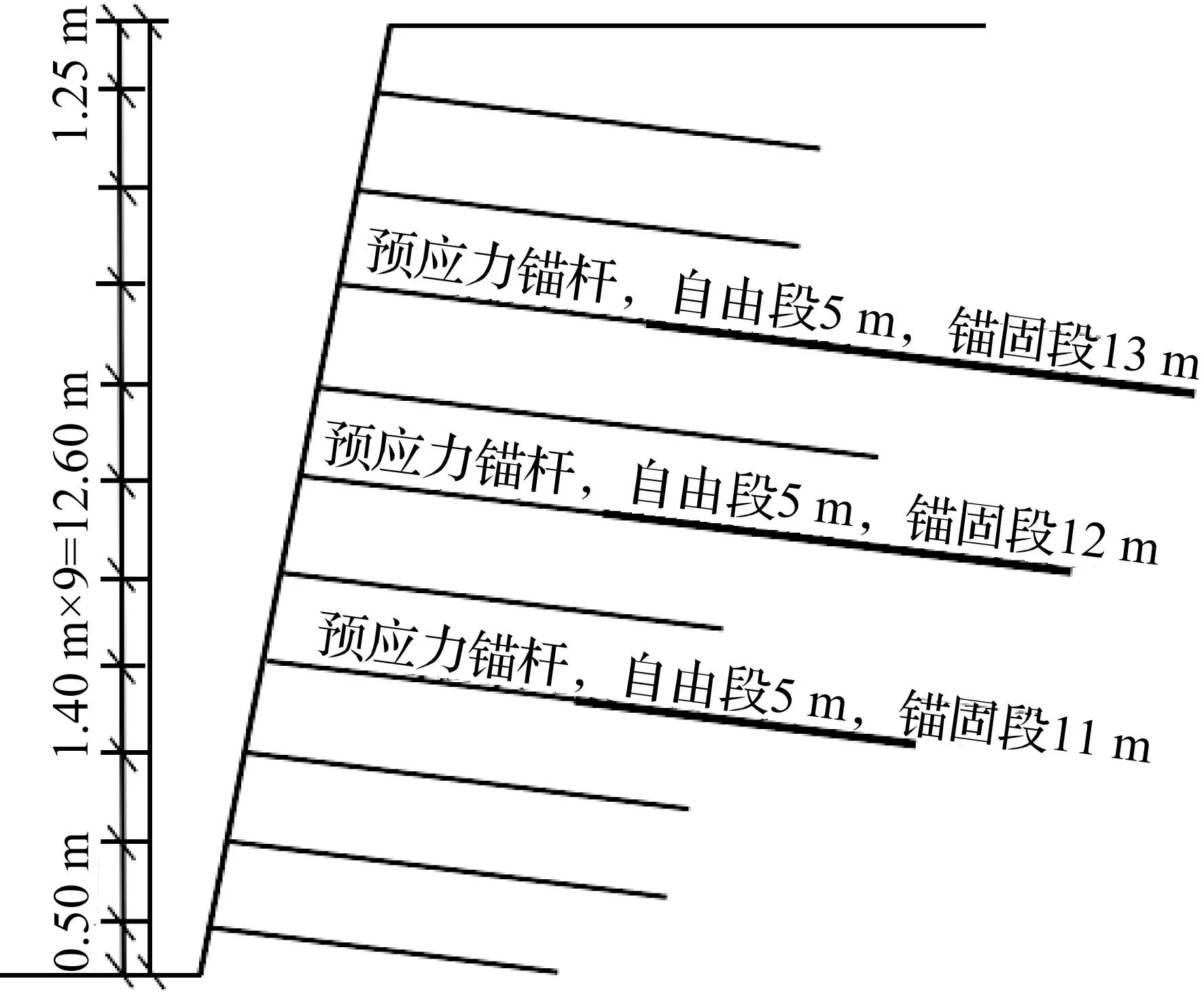
图5　深圳假日广场支护剖面图示Fig.5　Diagram on supporting profile ofShenzhen Holiday Plaza

4工程实例

4.1工程概况

深圳假日广场南侧的基坑深度为14.35 m，采用预应力锚杆复合土钉支护形式，坡度80°，共10层。支护剖面如图5所示。

第1、2、4、6、8、9、10层为土钉，从上到下长度分别为8 m，8 m，12 m，8 m，8 m，8 m，6 m；第3、5、7层为预应力锚杆，从上到下总长分别为18 m，17 m，16 m(自由段长度均为5 m)，锚杆的预张拉力均为200 kN。土钉水平间距取1.4 m，倾角均为15°，试验区域紧临深南大道，坡顶荷载q取 20 kPa。

开挖影响范围内的土体主要由填土、粉质黏土组成。土体力学参数如表1所示。填土平均厚度为0.6 m，粉质黏土平均厚度为13.75 m。根据表1中的力学参数，可得土体平均重度γ为19.54 kN/m3；土体黏聚力均值uc为24.37 kPa，均方差σc为10.17 kPa；内摩擦角均值uφ为19.5°，均方差σφ为11.59°；钉土界面黏结强度均值为39.58 kPa，均方差为9.59 kPa；内摩擦角正切值的均值为0.25，均方差为0.11。

表1　土层力学参数

4.2可靠性结果分析

应用Visual Basic 6.0对前面建立的内外部稳定性的极限状态功能函数编制程序迭代求出验算点c*,φ*,τ*，代入公式(3)，可得可靠性分析结果：

①外部稳定性分析结果，β=3.72，Pf=2.54×10-3。

②内部稳定性分析结果，β=3.54，Pf=7.82×10-3。

一般情况下，基坑支护属临时性工程，可靠指标β直接关系着安全性与经济性的平衡，目前尚未有明确的规定。美国建筑设计规范LRFD(60601-2001)中临时结构β的建议值是2.5；我国《建筑结构设计统一标准》(GBJ 68-84)对于各级建筑发生延性破坏的β建议值分别为3.7，3.2，2.7；Meyerhof指出基坑支护结构β的极限值是3.1。鉴于以上分析，考虑基坑支护属临时结构及延性破坏特点，土钉支护结构的可靠指标β的建议取值如表2所示。

表2　可靠指标β的建议取值

对于失效概率Pf，基于堤坝的失稳统计结果，一般以10-2～10-3作为判别依据。因此，可判定该基坑可以达到稳定标准。

5结论

①考虑岩土介质的变异性及不确定性，提出将可靠指标β用于加锚复合土钉支护体系稳定性分析的新思路，取土体参数c、φ和τ为影响复合支护体系安全储备的因素，并定义可靠指标；

②考虑土钉支护的加固机理，将土钉墙视为一个被加固的整体，外部分析时仅考虑锚杆的锚固作用，假定滑移面为圆弧形，建立复合支护体系的外部稳定分析模型；内部分析时综合考虑土钉与锚杆，假定滑移面为改进的双折线，建立复合支护体系的内部稳定分析模型；

③改进的双折线破裂面(拉裂面与土钉轴向垂直，滑移面通过坡脚)用于预应力锚杆复合土钉支护体系的内部稳定性分析，可以考虑土钉支护上部受拉、下部受剪的受力特征，简单、合理、有效。

参考文献：

[1]黄广龙，卫敏，李娟.参数变异性对围护结构稳定性影响分析[J]. 岩土力学，2010,31(8)：2484-2488.

[2]罗晓辉，朝泽东，肖坚.基于蒙特卡罗法的基坑土钉支护稳定可靠度分析[J]. 华中科技大学学报，2006,23(S1)：30-33.

[3]苏倩.框架预应力锚杆柔性支护结构的可靠度分析[D]. 兰州:兰州理工大学，2013.

[4]惠趁意，朱彦鹏，叶帅华.预应力锚杆复合土钉支护稳定可靠度分析[J]. 岩土工程学报，2014,36(S2)：186-190.

[5]熊赞民，隆威.深基坑预应力复合土钉支护稳定性的可靠性分析[J]. 矿业研究与开发，2004,24(2)：24-27.

[6]王辉，程建华，赵洪波.考虑预应力的复合土钉支护结构侧移计算[J]. 广西大学学报(自然科学版)，2014，39(4):828-832.

[7]程建华，王辉，刘云龙，等.深基坑主被动组合支护结构的协同工作及位移分析[J]. 广西大学学报(自然科学版)，2014,39(1)：119-123.

[8]YUAN J X, YANG Y W.New approach to limit equilibrium and reliability analysis of soil nailed walls[J]. International Journal of Geomechanics, 2003, 3(2): 145-151.

[9]PRADHAN B, THAM L G, YUE Z Q, et al.Soil-nail pullout interaction in loose fill materials[J]. International Journal of Geomechanics, ASCE，2006,6(4):238-247.

[10]WEI W B, CHENG Y M.Soil nailed slope by strength reduction and limit equilibrium methods[J]. Computers and Geotechnics, 2010, 37(5):602-618.

[11]SIVAKUMAR G L, SINGH V P.Reliability-based load and resistance factors for soil-nail walls[J]. Can Geotech, 2011, 48(6): 915-930.

[12]黄志全，王安明，毕理毅，等.深基坑支护工程可靠度分析与数值模拟[M]. 郑州：黄河水利出版社，2009.

[13]刘国彬，王卫东.基坑工程手册[M]. 2版.北京：中国建筑工业出版社，2009.

[14]陈昌富，彭小明.深基坑土钉墙外部稳定可靠度优化分析方法[J]. 湖南大学学报(自然科学版)，1999,26(2)：66-70.

(责任编辑唐汉民梁健)

Reliability analysis and demonstration of composite soil nailing retaining system enhanced with prestressed anchor

WANG Hui1， YANG Xiang-qian2， GAO Xin-jun3

(1. School of Civil Engineering, Henan Polytechnic University, Jiaozuo, 454003, China;

2. Planning and Architectural Design Institute of Zhoukou City, Zhoukou 466000, China;

3. School of Civil Engineering, Zhengzhou University, Zhengzhou 450001, China)

Abstract:To analyze and demonstrate composite retaining system enhanced with soil nails and prestressed anchors, some researches were carried out. In the analysis, a new idea based on reliability principle is presented. Firstly, considering the reinforcement mechanism of soil nailing, external stability of composite retaining system was analyzed based on the assumption of the circular-arc-shaped slip surface. Secondly, it was assumed that there was a double-line-shaped slip surface in internal stability study. Lastly, combined with an engineering example, the method of two-order-moment was adopted to analyze the limit state functions of external and internal stability models according to the recommended values of reliability index. The study indicates that the reliability index is suitable used to analyze the stability of composite retaining system, which considers the variability and uncertainty of soil compared with the conventional limit equilibrium theory; that modified double-line-shaped slip surface is simpler and more reasonable for the analysis of internal stability of composite retaining system, because it considers the mechanical characteristic of soil nailed wall, which is tensioned in the upper part and sheared in the lower part. The results can provide theoretical foundations and calculation references for engineering design.

Key words:composite soil nailing; prestressed anchor; reliability; stability analysis; slip surface

中图分类号：TU472

文献标识码：A

文章编号：1001-7445(2016)01-0212-07

doi:10.13624/j.cnki.issn.1001-7445.2016.0212

通讯作者：郜新军(1981—)，男，河南南阳人，郑州大学讲师，博士;E-mail: gxjun@zzu.edu.cn。

基金项目：国家自然科学基金资助项目(41072224)；河南理工大学2015青年基金项目(72511/118)

收稿日期：2015-06-12；

修订日期：2015-12-07

引文格式：王辉，杨向前，郜新军.加锚复合土钉支护体系可靠度分析与实证[J].广西大学学报(自然科学版)，2016，41(1)：212-218.