“归纳、类比与猜想”在小学数学中的教学应用

廖平安

(深圳市龙华新区清湖小学 广东 深圳 518000)

“归纳、类比与猜想”在小学数学中的教学应用

廖平安

(深圳市龙华新区清湖小学 广东 深圳 518000)

在小学数学教材中有许多法则、公式等，是按照从特殊到一般的认识规律，通过对特例的观察、分析、实验，从而归纳出一般性结论，即归纳法。类比在数学知识延伸拓展过程中常借助于比较、联想来启发诱导以寻求思维的变异和发散。在归纳知识系统时又可用来串联不同层次的类似内容，帮助理解和记忆。在解决问题时，无论是对于命题本身或解题方法，都是产生猜测、获得命题的推广或引伸的原动力。因此，归纳法和类比法既是数学学习的重要方法，也是数学发现的有效方法。归纳和类比都属于合情推理，其结论需要演绎证明。猜想是归纳与类比的成果，它们都包含有猜想的成分，所以猜想本身就是一种合情推理，直截了当一点，合情推理就是猜想。牛顿说过：“没有大胆的猜想，就做不出伟大的发现。”因此，合理地设计富有猜想的教学过程，不仅可以很好地组织教学，而且还可以提高学生学习兴趣，培养学生的创新能力。

1 归纳法

归纳法是通过对同一类事物的特殊对象的研究而得出一般性结论的方法，也就是由特殊到一般的推理方法。归纳法作为数学发现的一种重要方法，在小学数学的探究学习和再创造学习中应用非常广泛。尤其是在一些公式、法则、性质、规律等知识的推导往往是通过列举几个特殊的例子的基础上归纳出来的。因此教师在教学时，要给予足够的时间让学生进行观察、实验、操作，鼓励学生进行分析、比较，找出事物的共性和差异，并组织他们清楚地表达自己的思考过程与结果，学会简单解释归纳推理的过程与依据。

在小学数学归纳的教学，主要体现在以下几个方面。

1.1 法则的归纳

对于整数的加、减、乘、除的计算，都是通过几个具体的由易到难的例子，让学生在理解算理和口算方法的基础上探索计算的方法，最后进行交流和算法的总结，四则运算法则的得出就是运用了归纳法。

1.2 性质的归纳

商不变的规律，小数的性质、分数的性质、比的性质、比例的性质、等式的性质等等，是小学数学中重要的性质，这些性质的获得，也都是通过几个例子，让学生进行观察、探索、交流，最后归纳总结而得到的。

1.3 公式的归纳

小学数学的数量关系式有很多，其中典型的计算公式主要是图形的周长、面积和体积公式。这些计算公式，也都是通过具体动手操作，猜想并验证，进而归纳出来的。

1.4 定律的归纳

小学生最早学习的运算律是关于整数加法和乘法的运算定律，即加法交换律、加法结合律、乘法交换律、乘法结合律、乘法分配律。这些运算律的产生，也是通过计算几组算式来观察并猜想，从特殊到一般，从而归纳出来的。

1.5 规律的归纳

小学数学中的规律主要有图形、数列、算式的规律，乘法和除法的变化规律等。这些规律的发现页主要是通过一些具体的例子的观察、比较、联想，再提出猜想，这是归纳法的典型应用。比如，在乘法中，一个因数不变，另一个因数扩大到原来的几倍，积就扩大到原来的几倍。这也是通过运用归纳法得到的。

当然，在小学数学的教学中，学生的推理能力处于初步发展阶段，很难对发现的规律进行证明，一般情况下都是通过再举一些例子进行验证。引导学生在操作、观察等活动中学生进行分析、比较，找到简单的事物的共性与差异，探索给定情境中隐含的规律和变化趋势，验证通过归纳推理得出的结论是否正确，并能解释归纳推理的过程和依据。这些对学生的数学学习，对学生推理能力的发展有着实际的意义。

2 类比

类比法就是根据不同的两个(或两类)对象之间在某些方面的相似或相同，从而推出它们在其他方面也可能相似或相同的推理方法。它是以比较为基础的一种从特殊到特殊的推理方法。类比法是由此及彼以及由彼及此的联想方法，著名数学教育家波利亚指出“类比是一个伟大的引路人”，教师在教学中必须善于引导学生去联想、类比，才能充分调动学生的想象力，让他们通过比较去发现、去认识、去掌握知识。培养具有创造能力的人才，就要帮助他们学会归纳和类比。类比具有启迪思维、提供线索、举一反三的作用，对发展思维特别是创造性思维十分有利。和归纳一样，类比在小学数学中也随处可见。如通过类比，从加法、减法的运算性质(或定律)很容易联想到乘法、除法的相应的运算性质(或定律)，由除法中各部分之间的关系，容易联想到分数的基本性质等。

同时，类比法是系统掌握新知识、巩固旧知识，使新旧知识融会贯通的有效方法。数学的发展是一个不断地从原有知识向深度和广度推进的过程，所以，各个系统的知识与知识之间必然存在着相似之处，更何况，许多知识的发展就是类比发现的结果。在实际教学中，教师必须有意识地引导学生注意知识之间的比较，如分数与除法的类比，乘法与加法的类比等。从旧知识去发现新知识，这不仅仅能起到事半功倍的效果，还将会大大提高学生的学习兴趣，取得良好的学习效果。在小学的数学教学中，类比的应用主要体现以下几个方面。

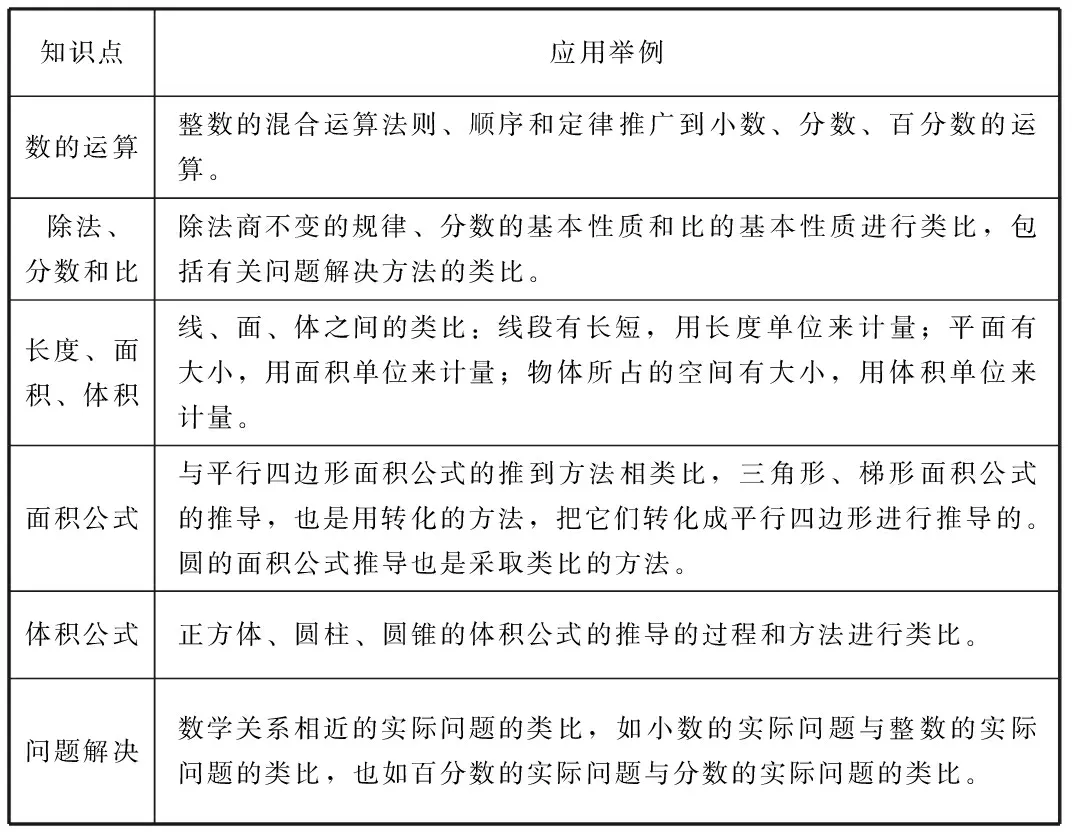
知识点应用举例数的运算整数的混合运算法则、顺序和定律推广到小数、分数、百分数的运算。除法、分数和比除法商不变的规律、分数的基本性质和比的基本性质进行类比,包括有关问题解决方法的类比。长度、面积、体积线、面、体之间的类比:线段有长短,用长度单位来计量;平面有大小,用面积单位来计量;物体所占的空间有大小,用体积单位来计量。面积公式与平行四边形面积公式的推到方法相类比,三角形、梯形面积公式的推导,也是用转化的方法,把它们转化成平行四边形进行推导的。圆的面积公式推导也是采取类比的方法。体积公式正方体、圆柱、圆锥的体积公式的推导的过程和方法进行类比。问题解决数学关系相近的实际问题的类比,如小数的实际问题与整数的实际问题的类比,也如百分数的实际问题与分数的实际问题的类比。

类比是发现的基础，是创新的前提。无论是学习新知识，还是利用已有的知识解决新问题，如果能够把新知识和新问题与已有的相类似的知识进行类比，进而找到解决问题的方法，体现了知识和方法的迁移。教学时，教师就可以启发、引导学生通过联想、类比来探索结果，提高解决问题的能力。应用类比，关键在于发现两类事物相似的性质，因此，观察、比较、联想是类比的基础。教师要鼓励学生细心观察、动手操作、比较分析，寻找新旧知识之间的联系，发展类比推理能力。

3 猜想

数学猜想是指根据某些数学现象而做出的预测性判断，以及做出这些判断的思维过程。数学家波利亚指出：“在证明一个数学定理之前，你先得猜想这个定理的内容，在你完全做出详细证明之前，你先得推测证明的思路，你先得把观察到的结果加以综合，然后加以类比。你得一次又一次地进行尝试。数学家的创造性工作成果，是论证推理，即证明；但这个证明是通过合情推理，通过猜想而发现的。”因此，在数学教学中必须重视猜想。学生在课堂上积极、主动地探究，需要猜想来引发。没有猜想，就不会有探究。徐利治说：“探索性思维中最关键的环节是提出一个有希望的合理的猜测。”猜想是探索性思维的方向，具有定位性、开拓性和创造性，是数学发现与数学证明的前兆。数学解题与数学发现一样，通常都是在通过类比、归纳等探测性方法进行探测的基础上，获得对有关问题的结论或解决方法的猜想，然后再设法证明或否定猜想，进而达到解决问题的目的。

当前新课程改革课堂教学的主要模式是创设情境，提出猜想(通过归纳或类比)，验证猜想(一般由合情推理来完成)，深化理解，总结提高。比如在教学3的倍数的特征时，因为学生已经积累了探索2和5的倍数特征的经验，因此对于3的倍数特征，教师可以放手先让学生进行大胆猜想。很多学生会理所当然地认为“末尾是3、6、9的数是3的倍数”，教师可以肯定学生的大胆猜想，鼓励学生举例一些3的倍数帮助验证，进行分析观察，对原猜想进行验证、修正、完善，从而得到正确的结论：3的倍数的特征是各个数位的数字之和是3的倍数。认识3的倍数特征之后，继续探究9的倍数的特征如何？教师引导，寻找3与9的关系，通过类比来引导学生提出猜想，并继续验证猜想，从而得到9的倍数的特征是：各个数位上的数字之和是9的倍数。

学生思维活跃，富于幻想，敢于猜想。但是，受知识、经验的限制，有时会提出一些幼稚可笑甚至错误的想法，这时教师非但不能讽刺打击，给予抹杀，反而应该加以鼓励，给予正确引导。让他们保持思维的积极性，给以他们敢想的勇气。因为这些看似可笑、错误的想法，总是蕴含着孩子们的创造性思维的成果。那些不拘一格的猜想，就是创造性思维的体现。

推理作为一般性的数学方法，对学生数学学习的可持续发展尤为重要。推理能力的形成和提高需要一个长期的、循序渐进的过程。数学教学活动的实质是数学推理，“合情推理”是小学生特别容易接受的一种推理方式，在小学阶段，教师应重视学生的数学思考，让学生形成推理的意识和习惯，这对于培养他们追求真理、实事求是的科学态度具有十分重要的意义。鉴于数学的严谨性，必须时适地引导学生对“合情推理”、“猜想”得到的结果给予严格说明(证明)的必要性。因为，只有经过合情推理、严格论证的结论，才具有真理性，谁也无法否认。而凡是偏离这两条原则获得的结论，不管怎样错综复杂、扑朔迷离，终究会被推翻或淘汰。

教学中，教师应给予平台让学生充分探究，亲身体验数学知识产生过程的一般方法，体会数学的思想和方法之魅力。小学生长期在这样的环境的熏陶下，敢于发现，敢于猜想，敢于创新，又有根据、有条理的思考问题的习惯将会慢慢地养成。

G623.5

A

1672-5832(2016)04-0157-02