基于改进碰摩力模型的迷宫密封-滑动轴承-转子系统动态特性

罗跃纲，吴　斌，智洪文，李艳秋

(大连民族大学 机电工程学院，辽宁 大连 116605)



基于改进碰摩力模型的迷宫密封-滑动轴承-转子系统动态特性

罗跃纲，吴斌，智洪文，李艳秋

(大连民族大学 机电工程学院，辽宁 大连 116605)

摘要：提出了一个新的改进碰摩力模型，建立了密封力和轴承油膜力双流体激励的转子系统非线性动力学方程，应用数值仿真方法分析了转静子碰摩非线性流固耦合动态特性。通过采用线性碰摩力模型和改进碰摩力模型进行比较分析说明采用改进碰摩力模型更能描述系统的碰摩故障特征。碰摩故障转子系统的响应在亚临界转速和超二阶临界转速区主要以拟周期运动为主，而在超一阶临界转速区则主要以周期分频运动为主要运动形式。

关键词：转子系统；Hertz接触模型；改进碰摩力模型；非线性特性

在旋转机械各类故障中，碰摩故障是国内外学者研究较早和较多的非线性故障之一。碰摩故障发生时，系统的动态过程比较复杂，振动响应表现出丰富的非线性特征。目前在碰摩故障研究中常采用的法向接触力模型主要有弹簧-阻尼模型[1-2]、Hertz接触模型、非线性阻尼模型[3]，常用的切向接触力模型主要有库仑摩擦模型、鬃毛模型[4-5](bristle model)和切向刚度模型[6]。Legrand等[7]提出了一种全三维接触准则来模拟叶片-机匣的碰摩行为，并分析了叶片-机匣接触的动力学特性。陈果[8]建立了转子-滚动轴承-机匣耦合系统动力学模型，充分考虑了由于滚动轴承的支撑刚度变化而产生的振动，发现在临界转速以前碰摩故障将产生较大的高次谐波，其中2倍频率较大；在临界转速以后，碰摩故障将产生较大的分数次谐波。Legrand等[9]基于机匣与叶盘系统的二维模型，研究了叶盘系统在机匣k节径模态振型下的接触问题，分析了转速对叶片-机匣接触碰摩的影响。张娅等[10]建立了双盘转子-轴承系统在轴向碰摩、径向碰摩以及两种碰摩共同冲击下的有限元法连续模型，采用计及了回转效应和剪切效应的梁单元，对转子系统在不同碰摩情况下的非线性动力学行为进行了数值模拟，研究了转子转速、转子系统上的不平衡量的分布以及碰摩刚度对系统的影响。刘杨等[11]运用基于Hertz接触理论的非线性碰摩力模型建模并进行数值仿真计算，对不同碰摩刚度下的故障转子系统动力学响应进行了研究。通过分析发现在碰摩刚度较大时，与线性刚度碰摩模型相比，采用Hertz接触理论碰摩力模型仿真出的结果非线性特性更强，系统碰摩特征更加明显，有利于判断碰摩故障的发生。曹登庆等[12]阐述了滞回碰摩力模型的物理意义，并与几种经典的碰摩力模型进行了比较；利用数值仿真的结果分析了静子刚度、转子偏心距等因素对采用滞回碰摩力模型的转子碰摩响应的影响。袁振伟等[13-14]基于Jeffcott转子模型，用六自由度方法研究了考虑气流激振的非线性流固耦合力的转子轴向和径向碰摩的动力学特性。殷玉枫等[15]应用Muszynska非线性密封力模型建立了在气流激振力作用下的转子-机匣碰摩系统耦合动力学方程，着重讨论了迷宫密封的物理和结构参数对碰摩转子运动特性的影响。本文综合各种模型的优缺点，提出了一个新的改进碰摩力模型，建立了密封力和轴承油膜力双流体激励的转子系统非线性动力学方程，应用数值仿真方法分析了转静子碰摩非线性流固耦合动态特性。

1碰摩转子系统模型和方程

带有碰摩故障的迷宫密封-滑动轴承-转子系统和碰摩力模型如图1，转子两端采用对称结构的滑动轴承支承，转子圆盘与轴承之间为无质量弹性轴。O1为轴瓦几何中心，O2为转子几何中心，O3为转子质心，k为弹性轴刚度，kC为转静子碰摩刚度。m1为转子在轴承处集中质量，m2为在圆盘处的等效集中质量。Fx、Fy分别为滑动轴承作用在转轴上的非线性油膜力，Px和Py为非线性密封力。

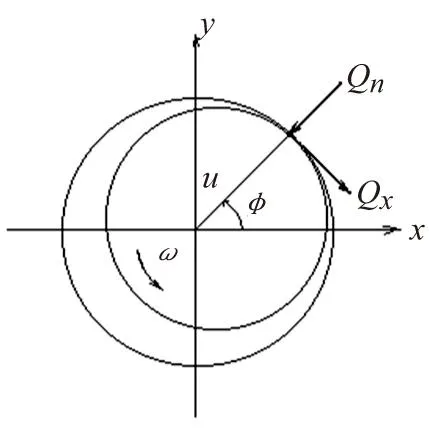
图1　碰摩故障迷宫密封-滑动轴承-转子系统与

在法向碰摩力模型方面，目前应用较多的是Hertz接触模型，其为一个非线性模型，冲击仅限于弹性变形，其原始形式不包括阻尼。其形式为

Qn=kCδn，

(1)

式中,k与n为和接触体材料、几何参数有关的常数，可通过接触力学理论计算得到。如两个球体发生正碰撞，n=3/2。k与泊松比、弹性模量以及两个球体的半径有关。

Hunt等[3]于1975年提出了同时考虑线性弹性力和线性阻尼力的碰撞力模型为：

Qn=(e-δ0)kC+cCv,Qτ=fQn，

(2)

式中,常数cC为接触碰撞的法向黏性阻尼系数。

在切向碰摩力模型方面，通常假设当碰摩发生时，转子与静子之间的摩擦力符合库仑摩擦定律，并假设摩擦系数为常数。但是当转静子相对速度很高时，转静子之间的摩擦系数与相对速度有关。对旋转机械转定子的弹性力学接触问题的研究表明，任何两个相对滑动的接触物体之间力与位移的关系是非线性的，其非线性程度与接触面的形状和接触物体的材料特性有关，因此必须考虑具有非线性接触刚度的问题。

综合以上模型的优缺点，本文提出一个新的碰摩力模型，该模型同时考虑了非线性弹性力和阻尼、以及碰摩发生时转静件间的相对速度和非线性接触刚度对非线性摩擦力的影响。

设静止时转定子之间的间隙为δ0，当碰撞发生时，其法向碰摩力与切向摩擦力可以表示为

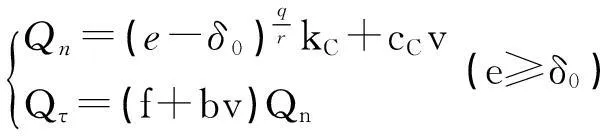
(3)

(e≥δ0)，

(4)

设转子左端的径向位移为x1，y1；转盘处的径向位移为x2，y2。则具有碰摩故障的密封-轴承-转子系统的运动微分方程为

(5)

式中：

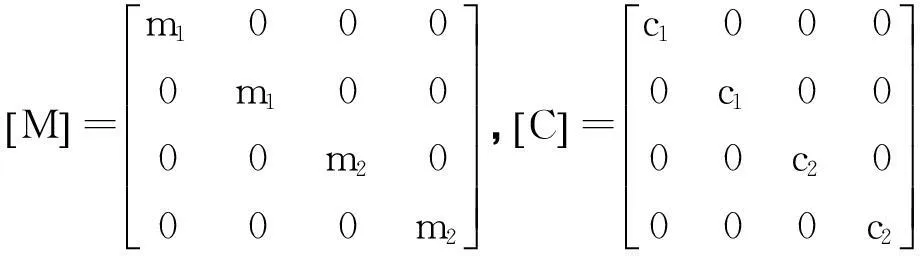
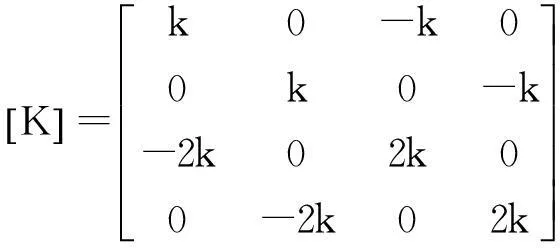
(6)

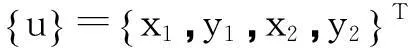
(7)

(8)

式中，Px和Py为非线性密封力分量[16]：

(9)

进行无量纲变换，得：

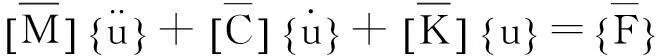
(10)

式中,

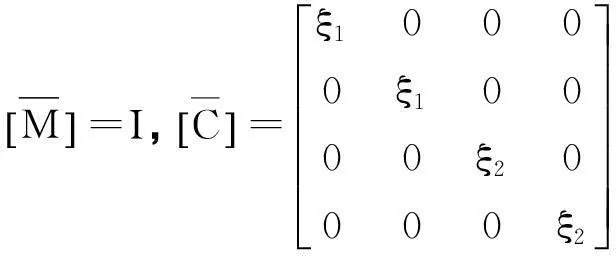
(11)

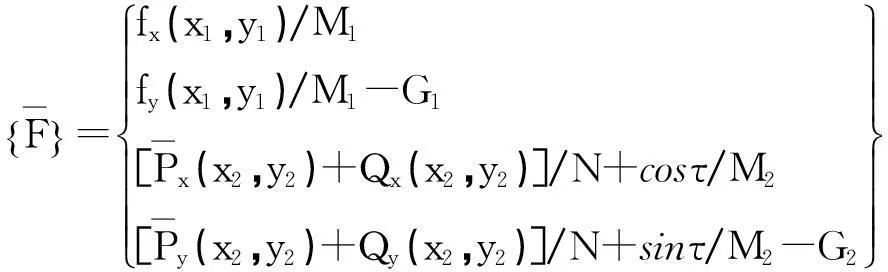
(12)

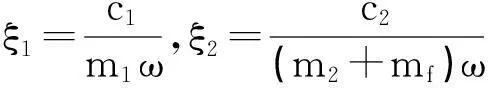
2数值仿真结果分析

鉴于系统的强非线性特性，本文利用数值仿真方法分析系统的动态特性。系统参数为：kC=3.5×106N/m，cC=1500N·s/m，f=0.1，b=0.02，q=3，r=2。转子系统的一阶临界转速为ω0=882.5rad/s。

采用线性碰摩力模型时系统的失稳转速是680rad/s，而改进碰摩力模型时的失稳转速是590rad/s。采用线性碰摩力模型和改进碰摩力模型时系统转速在ω=660rad/s(亚临界转速)时系统的轴心轨迹、x、y方向的幅值谱和Poincaré截面图分别如图2、图3。可见采用线性碰摩力模型时系统响应为稳定的周期1运动，从幅值谱图可见倍频成分，特别是y方向的2倍频成分；采用改进碰摩力模型时系统响应为拟周期运动，从幅值谱图可见明显的分频和倍频成分，包括0.1f-0.39f、0.40f-0.49f、0.5f及1f、2f、3f等，说明采用改进碰摩力模型更能准确地描述系统的碰摩故障特征。

系统转速在ω=1100rad/s(超一阶临界转速)时系统的轴心轨迹、x、y方向的幅值谱和Poincaré截面图如图4，系统此时的响应为周期2运动。系统转速在ω=1450rad/s(超一阶临界转速)时系统的轴心轨迹、x、y方向的幅值谱和Poincaré截面图如图5，系统此时的响应为周期8运动，幅值谱中分频成分特征明显。说明在超一阶临界转速时系统的响应主要以周期分频运动为主。

系统转速在ω=2000rad/s(超二阶临界转速)时系统的轴心轨迹、x、y方向的幅值谱和Poincaré截面图如图6，此时系统由于受到油膜力影响较大，幅值谱中有明显的不可公约的分频成分，其响应为拟周期运动。

图2　转速ω=660 rad/s时系统的响应

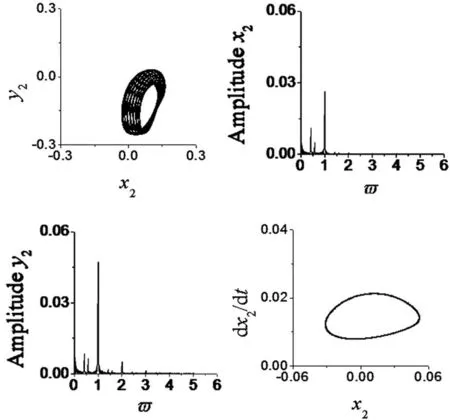
图3　转速ω=660 rad/s时系统的响应

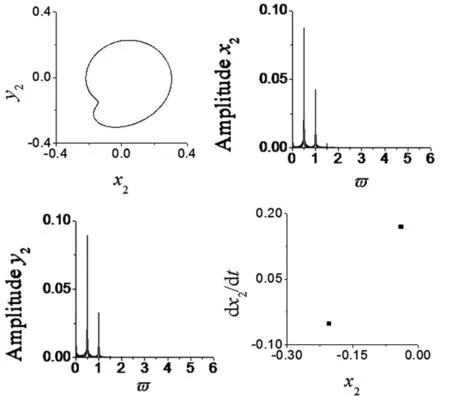
图4　转速ω=1100 rad/s时系统的响应

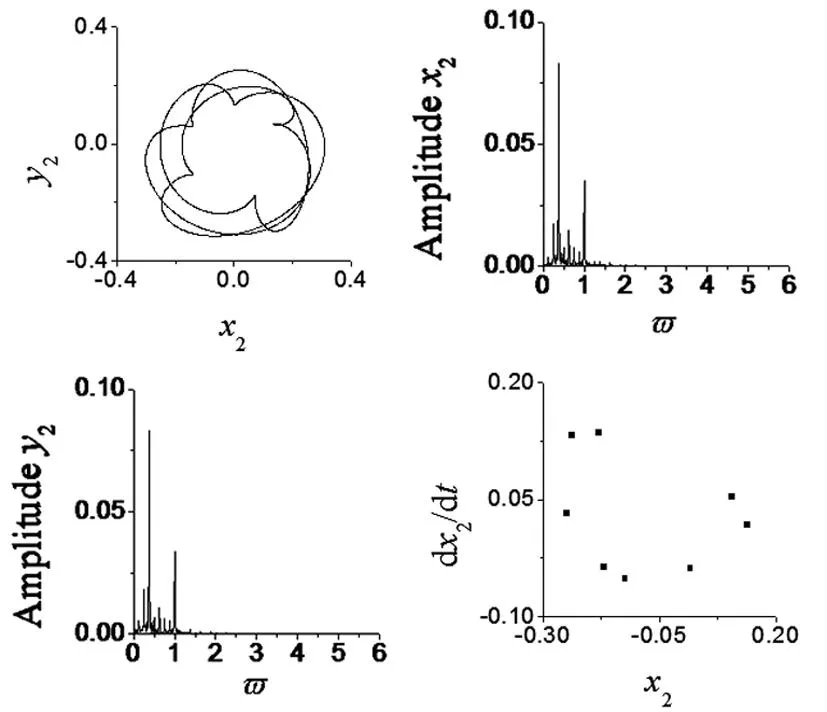
图5　转速ω=1450 rad/s时系统的响应

图6　转速ω=2000 rad/s时系统的响应

3结论

(1)提出了一个新的改进碰摩力模型，该模型综合了各种模型的优缺点，以此建立了密封力和轴承油膜力双流体激励下的碰摩转子系统非线性动力学方程，应用数值仿真方法分析了转静子碰摩非线性流固耦合动态特性。

(2)通过采用线性碰摩力模型和改进碰摩力模型进行比较分析说明采用改进碰摩力模型更能描述系统的碰摩故障特征。

(3)系统在的响应在亚临界转速和超二阶临界转速区主要以拟周期运动为主要运动形式，而在超一阶临界转速区则主要以周期分频运动为主。在低转速区域碰摩转子的分频和倍频特征更加明显。

参考文献：

[1]GILARDIG,SHARFI.Literaturesurveyofcontactdynamicsmodeling[J].MechanismandmachineTheory, 2002, 37(10): 1213-1239.

[2]MARKERTR,WEGENERG.Transientvibrationofelasticrotorsinretainerbearings[C].Proceedingsofthe7thInternationalSymposiumofTransportPhenomenaandDynamicsofRotatingMachinery,Honolulu,US:ISROMAC, 1998:764-774.

[3]HUNTKH,CROSSLEYFR.Coefficientofrestitutioninterpretedasdampinginvibroimpact[J].JournalofAppliedmechanics, 1975, 42(2): 440-445.

[4]HAESSIGDA,FRIEDLANDB.Onthemodelingandsimulationoffriction[J].JournalofDynamicSystems,MeasurementandControl, 1991, 113: 354-362.

[5]MAO.Contactdynamicsmodelingforthesimulationofthespacestationmanipulatorshandingpayloads[C].IEEEInternationalConferenceonRoboticsandAutomation,Nagoya,Japan, 1995: 1252-1258.

[6]LIMCT,STRONGEWJ.Obliqueelastic-plasticimpactbetweenroughcylindersinplanestrain[J].InternationalJournalofEngineeringScience, 1999, 37(1): 97-122.

[7]LEGRANDM,BARAILLYA,PIERREC.Fullthree-dimensionalinvestigationofstructuralcontactinteractionsinturbomachines[J].JournalofSoundandVibration, 2012, 331(11): 2578-2601.

[8] 陈果. 转子-滚动轴承-机匣耦合系统的不平衡-碰摩耦合故障非线性动力学响应分析[J]. 机械工程学报，2008，44(3)：82-88.

[9]LEGRANDM,PIERREC,PESEUXB.Structuralmodalinteractionofafourdegreeoffreedombladeddiskandcasingmodel[J].JournalofComputationalandNonlinearDynamics, 2010, 5(4): 13-41.

[10] 张娅，王维民，姚剑飞．双盘转子系统轴向-径向碰摩非线性动力学特性分析[J]. 振动与冲击，2012，31(12): 141-145.

[11] 刘杨，太兴宇，陈亚哲,等. 非线性油膜力作用下的碰摩转子系统动力学分析[J]. 机械设计与制造，2013，(3)：35-37.

[12] 曹登庆，杨洋，王德友,等. 基于滞回碰摩力模型的转子系统碰摩响应研究[J]. 航空发动机，2014，40(1)：1-9.

[13] 袁振伟，李志农，王三保,等. 转子轴向碰摩非线性流固耦合动力学特性全自由度分析[J]. 中国电机工程学报，2008, 28(14)：92-97.

[14] 袁振伟，王三保，岳希明,等. 转子径向碰摩非线性流固耦合动力学特性全自由度的动态分析[J]. 机械工程学报，2008, 44(6)：199-205.

[15] 殷玉枫，姚德臣，王松雷. 非线性转子-机匣密封碰摩系统的耦合振动分析[J]. 中国工程机械学报，2008,6(3)：269-275.

[16]MUSZYNSKAA,BENTLYDE.Frequencysweptrotatinginputperturbationtechniquesandidentificationofthefluidmodelsinrotor/bearing/sealsystemsandfluidhandingmachines[J].JournalofSoundandVibration, 1990, 143: 103-124.

[17]LUOYuegang,ZHANGSonghe,WUBin,etal.Dynamicanalysisonnonlinearfluid-structureinteractionforcesofrub-impactrotorsystem[J].TheOpenMechanicalEngineeringJournal, 2014, 8: 480-486.

(责任编辑王楠楠)

Dynamics Behaviours of Labyrinth Seal-sliding Bearing-rotor System

Based on Improved Rub-impact Force Model

LUO Yue-gang, WU Bin, ZHI Hong-wen, LI Yan-qiu

(College of Mechanical and Electronic Engineering, Dalian Minzu University, Dalian Liaoning 116605, China)

Abstract:A new improved rub-impact model was put forward and the nonlinear dynamincs fomula of the rotor system was set up considering the seal fluid force and oil-film force. The dynamic characteristics of the rub-impact rotor system were analyzed by numerical simulation method. It showed that the improved rub-impact model can describe the characteristics of rub-impact fault better compared with the linear rub-impact. The responses of the rub-impact rotor system were quasi-periodic motions in the region of sub-critical and ultra-supercritical rotational speed, and periodic-k motions in the region of sub-critical rotating speed.

Key words:rotor system; Hertz contact model; improved rub-impact model; nonlinear characteristics

中图分类号：O322,TH113

文献标志码：A

文章编号：2096-1383(2016)01-0033-05

作者简介：罗跃纲(1964-)，男，辽宁锦州人，教授，博士后，大连民族大学优秀学术带头人，主要从事非线性振动、转子动力学、智能故障诊断及振动利用工程研究。

基金项目：辽宁省教育厅基金资助项目(L2014545)；中央高校基本科研业务费专项资金资助(DC201502010202)。

收稿日期：2015-12-15