基于粒子松密度的复杂网络社团划分算法

姜 斐,王晓军,许 斌,亓 晋

(1.南京邮电大学 计算机学院、软件学院，江苏 南京 210003；2.南京邮电大学 物联网学院，江苏 南京 210003)

基于粒子松密度的复杂网络社团划分算法

姜 斐1,王晓军1,许 斌2,亓 晋2

(1.南京邮电大学 计算机学院、软件学院，江苏 南京 210003；2.南京邮电大学 物联网学院，江苏 南京 210003)

复杂网络的社团挖掘算法是近几年数据挖掘领域新兴起的一个热点课题。传统的智能优化算法虽然在社团挖掘方面有较好的效果，但其执行效率低，适用范围窄；而已有的启发式算法虽然在社团挖掘效率方面的优势比较明显，但相比于智能优化算法，其普适性仍未得到改善。为综合提高社团划分算法的效率，通过对材料科学领域的松密度的概念进行调研，结合复杂网络的特有属性，提出一种基于节点松密度的社团挖掘算法。实验结果表明，相比于其他算法，该算法在时间和精度上都有较为显著的优势。

复杂网络；松密度；社团；挖掘

0 引 言

复杂网络是对复杂系统的抽象和描述方式，任何包含大量组成单元(或子系统)的复杂系统，当把构成单元抽象成节点、单元之间的相互关系抽象为边时，都可以当作复杂网络来研究[1]；复杂网络是研究复杂系统的一种角度和方法，它关注系统中个体相互关联作用的拓扑结构，是理解复杂系统性质和功能的基础[2]。因此，在科学发展日趋复杂化的大背景下，网络社团挖掘算法的研究对分析复杂系统中的复杂网络拓扑结构、理解其功能、发现其隐含模式、预测其行为具有十分重要的理论意义[3]。

1 网络社团划分算法

网络社团结构是复杂网络最普遍和最重要的拓扑属性之一[4]，处于相同社团内的节点间相互连接密集、处于相异社团的节点间相互连接稀疏；该特点也是对复杂网络的社团结构的定义[5]。

几乎所有的已知的社团聚类算法都直接或间接地应用了社团的这一特点进行计算[6]。在已知的应用到此领域的智能优化算法中，MODPSO(多目标粒子群算法)是效果比较好的一个，该算法将复杂网络的模块密度D的概念[7]进一步分解为RA和RC并将其作为算法的两个优化目标[8]。

在MODPSO算法的核心的局部搜索部分,根据某一节点的邻居节点的所占社团的比例进行该节点的社团归属划分。该算法的实验结果表明，局部搜索这一应用使得算法的效率有了显著的提升；从社团定义的角度对其进行分析不难看出，对于一个社团内的某个节点的邻居节点在同一社团的比例明显要大于在不同社团的比例；同时在模块密度的公式中也可以看到对网络社团定义的间接应用。

(1)

(2)

D=RA-RC

(3)

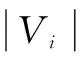
MODPSO算法通过局部搜索不断优化RA和RC，使得RA不断增大，RC不断减小，最终得出网络聚类结果。模块密度能够很好地反映网络社团聚类情况的优劣程度，文中算法也会用到这一指标对实验结果进行评测。实验数据显示，MODPSO算法对于部分网络聚类精度高，但该算法也同样具有智能优化算法的普遍缺陷—效率低[9]。

与智能优化算法相比，启发式算法在效率方面则有较大的优势[10]。启发式算法根据网络的节点与节点之间的内在联系(如度、介数及聚类系数)等，对节点进行聚少成多的社团构造[11]。不同的网络指标应用到聚类算法中有不同的优缺点：基于节点度的聚类算法，简单直观，便于计算，但忽略了网络的整体特性，结果不够准确；基于中介数的聚类算法按节点的流量分析节点的重要性，可以反映网络的动态特性，但算法复杂度过高，执行效率低；基于特征向量的聚类算法考虑到了邻居节点的重要性，但仅仅将各个节点进行简单的线性叠加，过于简化实际情况。

基于数据场的复杂网络聚类算法是一种典型的启发式聚类算法[12]，在算法中首次将势场和互信息的概念融合应用到复杂网络聚类问题。首先，将节点的互信息作为衡量节点重要性的指标，根据节点互信息的大小划分出网络社团的核心节点；然后，通过计算每个非核心节点与核心节点的势值判断节点的社团归属。该算法执行效率较高，但其具有一定的局限性，只能对部分网络具有较好的聚类结果。

文中通过对大量网络数据集的拓扑结构进行调研，提出一种基于度和粒子松密度的粒子社团聚类算法；根据节点的度数划分核心节点很容易忽略网络的整体特性，而网络松密度的概念则可以较好地弥补这一缺陷。将节点按照度大小进行降序排列，序列的第一个节点选为第一个粒子社团的核心节点；然后依次计算每个节点与核心节点的松密度，根据松密度的大小判断该节点是否为新的粒子社团的核心节点。

2 粒子社团聚类算法

文中算法将网络中的每个节点形象化为微粒，则根据网络社团的定义，连接紧密的微粒聚集在一起形成粒子社团。

2.1 粒子松密度

粒子松密度的概念来自于微粒学中的松密度的定义。在微粒学中，松密度指的是包括颗粒内外孔及颗粒间空隙的松散颗粒堆积体的平均密度。用处于自然堆积状态的未经振实的颗粒物料的总质量除以堆积物总体积求得，公式如下：

bulk=m/V

(4)

在粒子社团运算中，用节点数代替堆积物质量m，节点之间的连接数代替堆积物的体积V，则网络总体的粒子松密度B为：

(5)

其中，Nnode表示网络中总的节点数；Nedge表示网络中总的边数。

任意两个节点的粒子松密度Bij为:

(6)

其中，Aij表示网络的邻接矩阵中i行j列的值；di和dj表示节点i和j的度；δ(i,j)表示节点i和j邻居节点的重复个数。

2.2 算法流程

考虑到节点的度值较大的点对网络中部分社团的划分的影响比较大，因此文中算法根据节点的度值计算该节点是否为某一社团的核心节点。首先，设定度值最大的节点为第一个社团的核心节点；然后，按节点度值的降序次序依次根据如下条件判断每个节点是否为核心节点:

(7)

若满足式(7)，则节点j不是新社团的核心节点，将其加入到核心节点为i的社团中；否则节点j为新社团的核心节点。式中λ的取值为节点j对核心节点i的影响度，根据实验数据表明，λ的取值与网络整体的粒子松密度密切相关，在实验分析部分会对其进行详细描述。

算法的具体执行步骤如下：

Step1：对网络中的节点进行度值的降序排列，得到节点序列S。

Step2：从序列S取出第一个节点作为网络中的第一个社团的核心节点，将该节点加入到核心节点序列C中。

Step3：依次取出序列S中的第二个节点，根据式(7)计算该节点与序列C中的节点是否满足构成核心节点的条件；若满足则将该节点加入序列C，若不满足则将该节点加入到对应的核心节点所在社团。

Step4：重复Step3，依次遍历序列S中的所有节点。

在算法核心步骤Step2和Step3的执行过程中分别会对网络节点进行一次遍历，算法的时间复杂度为O(n2)。

3 仿真实验与分析

文中算法运行的硬件环境为Inter(R)Core(TM)i5-4200UCPU，1.60GHz，4GB内存。软件环境为微软Windows8.1操作系统，jdk1.7，Eclipse软件开发环境，采用Java语言进行实现。

实验数据的验证采用国际通用的NormalizedMutualInformation(NMI)指标进行实际划分结果与文中算法划分结果的对比[13]，该指标的值表示两个向量的相似度，其取值范围为(0,1)。文中用其作为实验结果的社团号向量与真实社团号向量的相似度，若NMI=1，则两向量完全相同；反之则完全不同。在对比过程中输入两个向量A和B，向量的第i位表示第i个节点所归属的类。

NMI(A,B)的计算公式如下：

其中，CA(CB)表示向量A(B)中的社团个数；C为向量A与向量B组成的混合矩阵，Cij表示向量B的第g个社团与向量B的第j个社团所共有的元素个数，Ci.(C.j)表示在矩阵C的第i行(j列)中所有元素之和；N为网络中的节点个数。

文中对人造数据集及具有代表性的部分公共数据集如海豚网络(dolphinnetworks)[14]、书局网络(polbooksnetworks)[15]、空手道俱乐部网络(karatenetworks)等[16]进行了对比测试。通过对实验结果的分析证明文中算法相对其他算法而言具有良好的划分效果和较高的执行效率。

3.1 人工网络数据集实验分析

人工网络数据集是由人工生成的严格符合网络社团定义的网络数据集，该数据集包含50个节点、808条边，该数据集的粒子松密度值为0.062。

按照网络社团划分的标准，该数据集共有5个社团，通过文中算法对其运算得出的社团聚类结果与原始聚类结果相同，该网络的拓扑结构如图1所示。

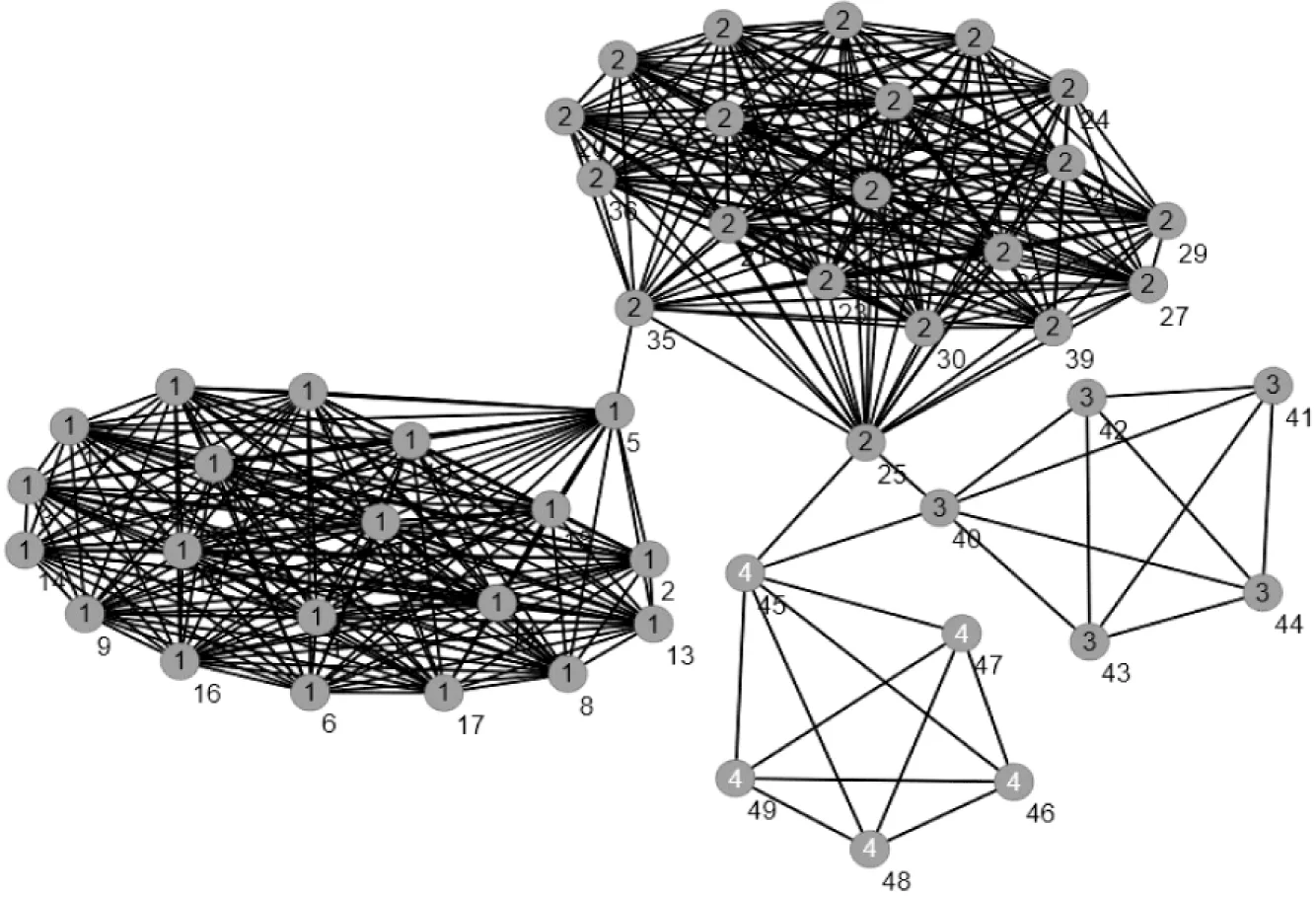
图1 人工数据集网络拓扑图

实验数据的NMI值为1表明文中算法的社团聚类结果与原始结果相同。实验分别对λ取值0.1～0.9，这9个取值中对应该结果的λ的取值为0.1和0.2，其他取值对应的NMI值均为0.887。

3.2 海豚网络实验数据分析

该数据集由Lusseau等在新西兰对62只宽吻海豚的生活习性进行了长时间的观察得出，根据研究发现这些海豚的交往呈现出特定的模式，并构造了包含有62个节点的海豚网络。如果某两只海豚经常一起频繁活动，那么网络中相应的两个节点之间就会有一条边存在。该数据集含有159条边，其粒子松密度值为0.39。该数据集的实际社团结构有一定主观因素，共有两个社团。当λ取0.4时，文中算法对其的聚类结果与真实结果相符。取不同λ对应实验结果的最优解比例如图2所示。当λ取值在网络整体的粒子松密度附近时，实验结果与原始聚类结果之间的差异将逐渐变小。其网络的拓扑结构如图3所示。

3.3 书局网络实验数据分析

书局网络数据集包含105个节点，节点之间连接的边数有159条，网络的粒子松密度值为0.39。

该网络数据集实际社团的结构如图4所示。从该拓扑结构中可以明显观察出其并不完全符合网络社团的定义：1号社团中的大部分节点都与其他社团连接紧密。按照该社团结构计算的模块密度D的值为2.019。根据文中算法聚类过后的数据集如图5所示，算法对原数据集的社团进行了部分修正，将1号社团中的部分节点重新进行聚类，当取值为0.4时，对应的模块密度值最大，为4.054。从拓扑结构和数据上进行比较，结果表明文中算法的聚类结果明显优于实际的聚类结果。

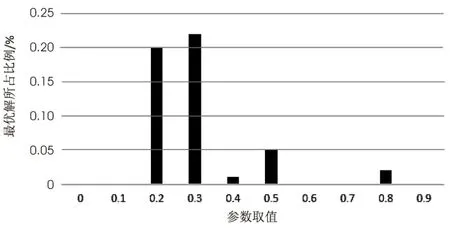
图2 不同λ取值对海豚网聚类的影响

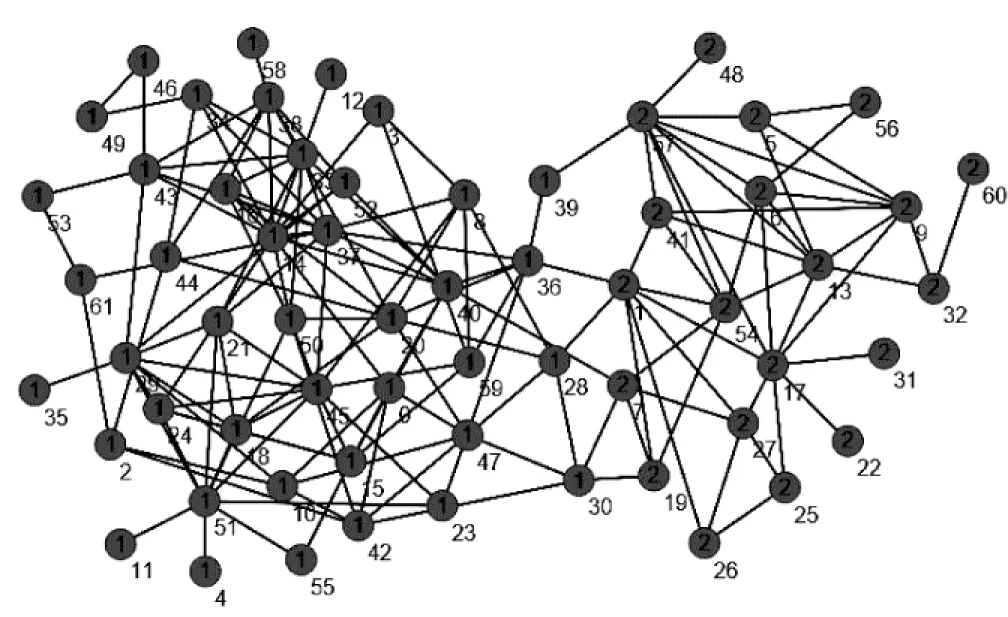
图3 海豚网络拓扑图

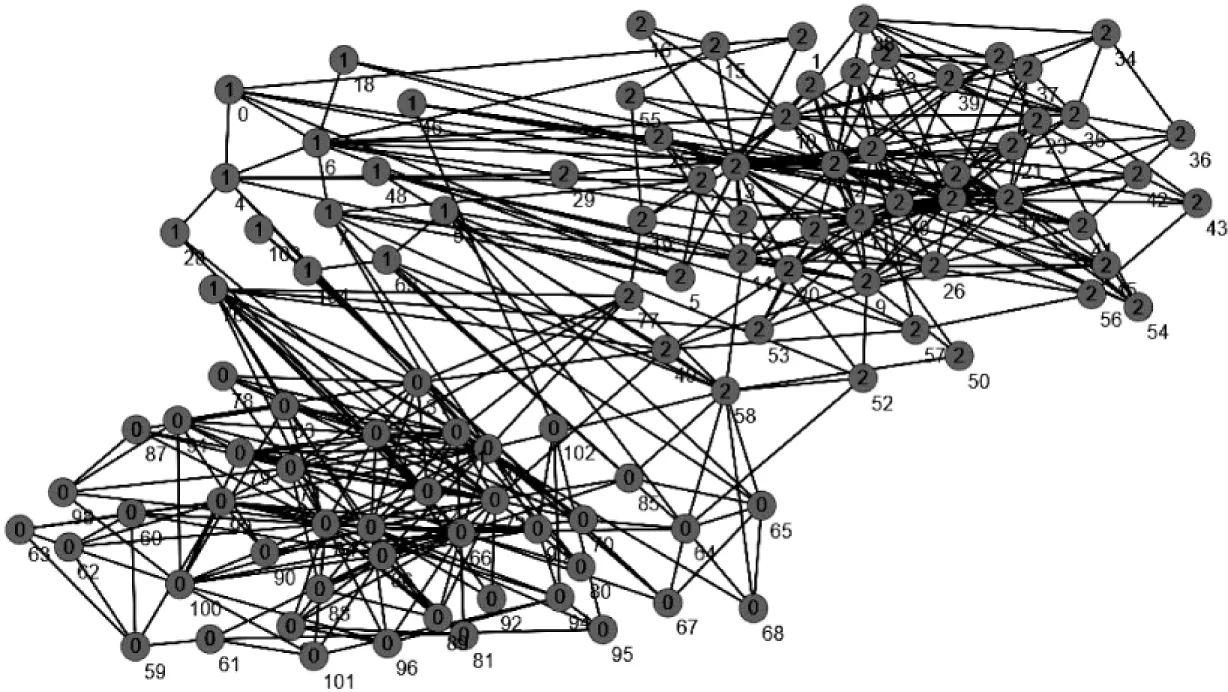
图4 书局实际社团聚类拓扑图

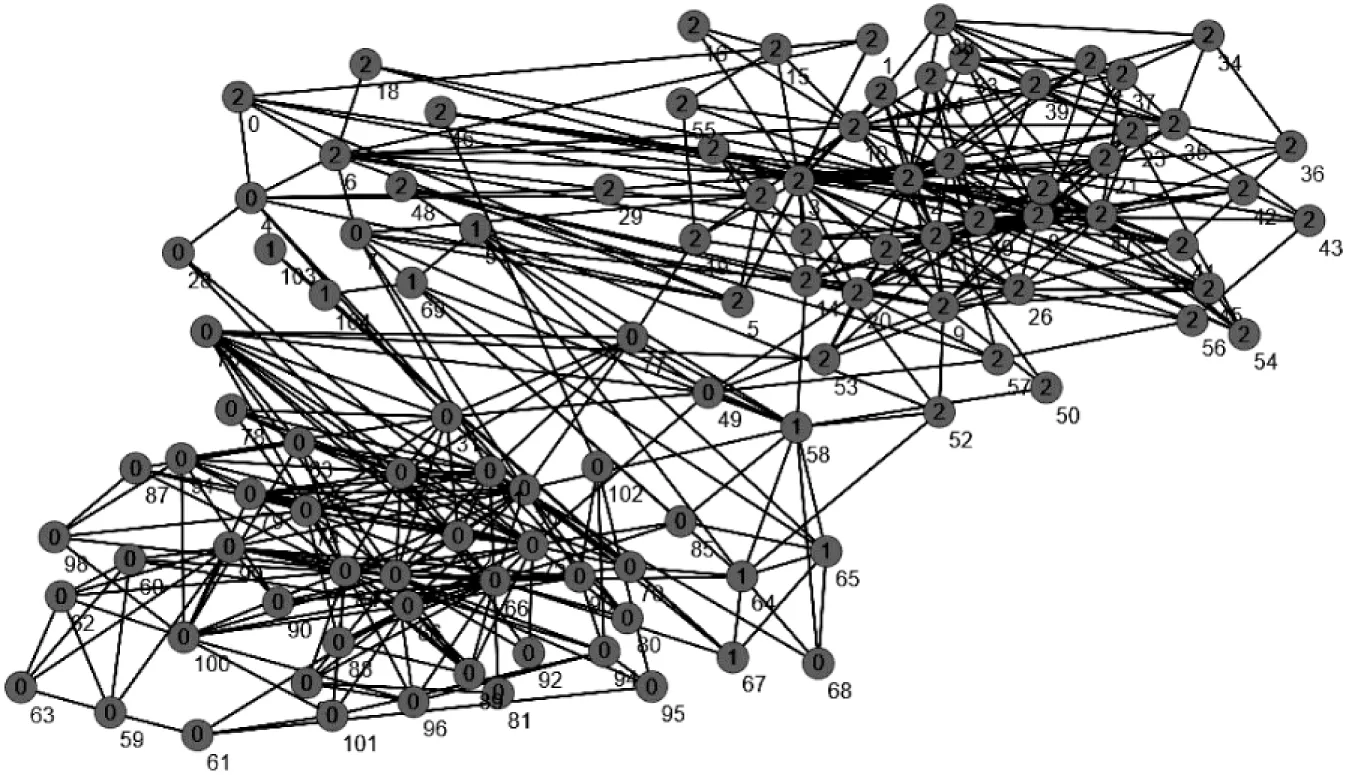
图5 文中算法对数据网络聚类拓扑图

3.4 空手道俱乐部网络数据集测试

空手道俱乐部数据集包含34个节点，节点之间连接的边数为78，网络的粒子松密度值为0.436。网络数据集的拓扑结构如图6所示。当取值为0.1～0.4时，NMI=1得出的聚类结果与实际聚类结果相符；取值为0.5～0.9时，NMI值为0.454与真实结果有偏差。

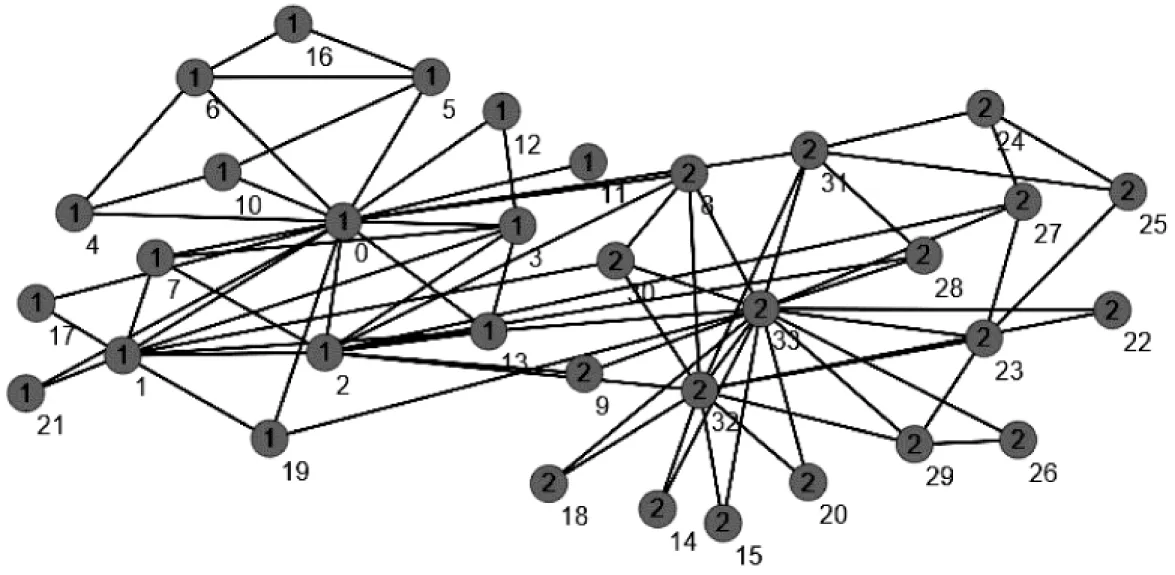
图6 空手道俱乐部网络拓扑图

3.5 小 结

通过对各个数据集的实验数据分析可以判断，λ的取值对于文中算法的聚类效果具有较大影响。边数比较密集的网络中，其网络的粒子松密度则偏小，因此合并节点i和j时，需要将Bij的值适当调大。λ的意义即是针对稀疏度不同的网络来调整节点之间合并的条件。文中算法经过实验数据测试得出λ与网络整体的粒子松密度有着直接联系，同时，实验结果表明，文中算法对于符合社团基本定义的网络可以给出准确的聚类结果。

4 结束语

对于复杂网络进行社团划分的算法种类繁多，皆是优缺点兼有。文中算法结合度值和粒子松密度的概念逐步对网络节点进行聚类。通过对实验数据的分析得出，不同网络的社团结构与网络整体的稀疏程度有着密切的联系:稀疏的网络社团内的节点连接也比较稀疏，但相比社团之间的连接要紧密；稠密的网络社团之间的连接比较稠密，但相对比社团内的连接仍然稀疏。文中算法能准确地利用网络整体的稀疏度来对网络进行聚类分析。实验结果表明，文中算法可按网络社团聚类的基本原理给出较优的社团结构，效率较高。

[1]LiuH,CaoM,WuCW.Couplingstrengthallocationforsynchronizationincomplexnetworksusingspectralgraphtheory[J].IEEETransactionsonCircuitsandSystemsI:RegularPapers,2014,61:1520-1530.

[2]KangS,BaderDA.Largescalecomplexnetworkanalysisusingthehybridcombinationofamapreduceclusterandahighlymultithreadedsystem[C]//Procof2010IEEEinternationalsymposiumonparallelanddistributedprocessing,workshopsandPhdforum.Atlanta,GA,UnitedStates:IEEE,2010.

[3]PeiT,ZhangH,LiZ,etal.Surveyofcommunitystructuresegmentationincomplexnetworks[J].JournalofSoftware,2014,9(1):89-93.

[4]NewmanMEJ.Thestructureofscientificcollaborationnetworks[J].ProceedingsoftheNationalAcademyofSciencesoftheUnitedStatesofAmerica,2001,98:404-409.

[5]LiZ,ZhangS,WangRS,etal.Quantitativefunctionforcommunitydetection[J].PhysicalReviewE,2008,77:036109.

[6]YangB,LiuDY,LiuJ,etal.Complexnetworkclusteringalgorithms[J].JournalofSoftware,2009,20(1):54-66.

[7]GongMG,CaiQ,ChenXW,etal.Complexnetworkclusteringbymultiobjectivediscreteparticleswarmoptimizationbasedondecomposition[J].IEEETransactionsonEvolutionaryComputation,2014,18(1):82-97.

[8]LeskovecJ,LangKJ,MahoneyM.Empiricalcomparisonofalgorithmsfornetworkcommunitydetection[C]//Procof19thinternationalworldwidewebconference.Raleigh,NC,UnitedStates:[s.n.],2010:631-640.

[9]TongC,NiuJW,DaiB,etal.Complexnetworksclusteringalgorithmbasedonthecoreinfluenceofthenodes[C]//Procof2012IEEE31stinternationalperformancecomputingandcommunicationsconference.[s.l.]:IEEE,2012:185-186.

[10]LiuX,LiD,WangS,etal.EffectivealgorithmfordetectingcommunitystructureincomplexnetworksbasedonGAandclustering[C]//Procof7thinternationalconferenceoncomputationalscience.Beijing,China:[s.n.],2007:657-664.

[11]TongC,NiuJW,DaiB,etal.Anovelcomplexnetworksclusteringalgorithmbasedonthecoreinfluenceofnodes[J].ScientificWorldJournal,2014,2014:801854.

[12]LiuYH,JinJZ,ZhangY,etal.Anewclusteringalgorithmbasedondatafieldincomplexnetworks[J].JournalofSupercomputing,2014,67(3):723-737.

[13]DanonL,Díaz-GuileraA,DuchJ,etal.Comparingcommunitystructureidentification[J].JournalofStatisticalMechanicsTheory&Experiment,2005,2005:P09008.

[14]LusseauD,SchneiderK,BoisseauOJ,etal.Thebottlenosedolphincommunityofdoubtfulsoundfeaturesalargeproportionoflong-lastingassociations[J].BehavioralEcology&Sociobiology,2003,54:396-405.

[15]NewmanME.Findingcommunitystructureinnetworksusingtheeigenvectorsofmatricies[J].PhysicalReviewE,2006,74:036104.

[16]GirvanM,NewmanMEJ.Communitystructureinsocialandbiologicalnetworks[J].ProceedingsoftheNationalAcademyofSciencesoftheUnitedStatesofAmerica,2002,99:7821-7826.

Community Clustering Algorithm in Complex Networks Based on Bulk Density

JIANG Fei1,WANG Xiao-jun1,XU Bin2,QI Jin2

(1.School of Computer Science and Technology,School of Software，NJUPT,Nanjing 210003,China;2.School of Internet of Things,NJUPT,Nanjing 210003,China)

The association clustering algorithm of complex networks is a new emerging hot topic in the field of data mining.Traditional intelligent optimization algorithm has better effect in clustering,but it has low execution efficiency and narrow application scope.Although some heuristic algorithm has obvious advantages of clustering efficiency,but compared with the intelligent optimization algorithm,universality still has not be improved.To improve the efficiency of community division algorithm,through the research of the concept of bulk density in the field of materials science,puts forward a kind of association clustering algorithm based on bulk density.The experiment shows that the algorithm proposed has obvious advantage in time and precision compared with other algorithms.

complex networks;bulk density;community;clustering

2015-11-23

2016-03-04

时间：2016-09-19

国家自然科学基金资助项目(61401225)；中国博士后科学基金资助项目(2015M571790)

姜 斐(1992-)，男，硕士研究生，研究方向为数据挖掘；王晓军，副研究员，硕士生导师，研究方向为分布计算技术与应用。

http://www.cnki.net/kcms/detail/61.1450.TP.20160919.0839.004.html

TP301.6

A

1673-629X(2016)10-0060-04

10.3969/j.issn.1673-629X.2016.10.013