平板断裂问题的多尺度扩展有限元法

胡　凯，尹硕辉

(河海大学 力学与材料学院，江苏 南京 211100)



平板断裂问题的多尺度扩展有限元法

胡凯，尹硕辉

(河海大学 力学与材料学院，江苏 南京 211100)

摘要：采用渐进弯曲奇异函数和跨过裂纹面的不连续函数，加强常规的位移逼近空间，从而使计算网格独立于裂纹，建立了贯穿裂纹Reissner-Mindlin板的多尺度扩展有限元法。在裂纹附近区域采用小尺度网格，其他区域采用大尺度网格。在计算代价不大的情况下，考虑大型结构中小裂纹的存在或者提高裂纹附近的精度。所有尺度单元都采用四结点四边形板单元，四边形任意结点板单元连接不同尺度单元。用互作用积分法计算裂尖应力强度因子，算例分析检验了本文方法的精度和有效性。

关键词：Reissner-Mindlin板；贯穿裂纹；多尺度；扩展有限元法；四边形任意结点板单元；应力强度因子

0引言

板结构在船舶与海洋工程领域有着重要的作用，在服役期不可避免会出现裂纹，致使结构在满足强度要求下发生破坏并可能造成严重的灾难，因此，有必要研究板结构的力学行为[1]。鉴于问题的复杂性，数值模拟是分析开裂板力学性能最有效的方法。扩展有限元法(extended finite element method，XFEM)[2]是目前分析不连续问题最有效的数值方法，已成功用于求解裂纹[3-6]、孔洞夹杂[7]、剪切带演化[8]、接触[9]和多相流[10]等问题。

结构分析中考虑到裂纹附近(特别是裂尖附近)存在高梯度场量[11]，因此，裂纹附近必须采用小尺度单元。若整个结构采用小尺度单元，则计算量巨大。为此，通常在远离裂纹区采用大尺度单元，这样就出现了不同尺度问题，需要采用多尺度计算方法进行求解。多尺度计算方法可分为基于均匀化的方法和基于层次分解技术的整体-局部法两种。基于均匀化的多尺度法存在尺度分离和周期性的局限[12]；基于层次分解技术的整体-局部法的思想是在关注的子域采用小尺度网格，在其他子域使用大尺度网格，能克服均匀化法的局限性。文献[13-16]将这两种多尺度计算方法和 XFEM 相结合进行断裂问题的多尺度分析。

基于层次分解技术的整体-局部法的多尺度计算，在不同尺度单元间存在一层任意结点单元。若能构造任意结点单元，则可方便地处理不同尺度单元的连接问题。文献[17]基于Reissner-Mindlin板理论构造了四边形任意结点板单元。本文建立了Reissner-Mindlin板断裂分析的多尺度XFEM，所有尺度的单元均采用四结点四边形单元，四边形任意结点板单元连接不同尺度单元，用互作用积分法计算应力强度因子。并给出算例分析，检验本文建立的多尺度扩展有限元法求解板断裂问题的效果。

1Reissner-Mindlin板理论

图1是厚度为t的贯穿裂纹板，其中，Γd为裂纹面。根据Reissner-Mindlin板理论，板内任一点的位移可以表示为：

u=zβy(x,y)；v=-zβx(x,y)；w=w(x,y)，

(1)

图1　贯穿裂纹的Reissner-Mindlin板

其中：βx和βy为板中面法线分别绕x轴和y轴的转角；w为板的挠度。

板中面应变可以表示为：

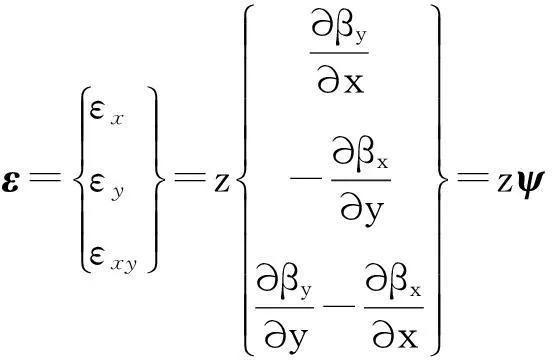
(2)

横向剪应变为：

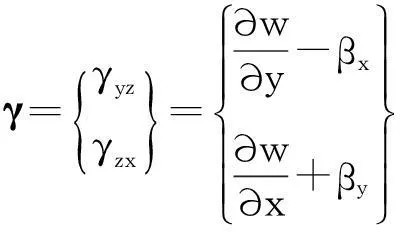
(3)

对于各向同性弹性板，应力-应变本构关系可表示为：

(4)

其中：E和ν分别为弹性模量和泊松比；k为横向剪应力修正因数，一般取5/6。

弯矩M和横向剪力Q定义为：

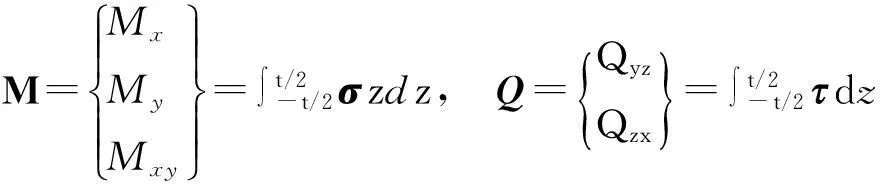
(5)

将式(4)代入式(5)得到：

M=Dbψ，Q=Dsγ，

(6)

板的势能为：

(7)

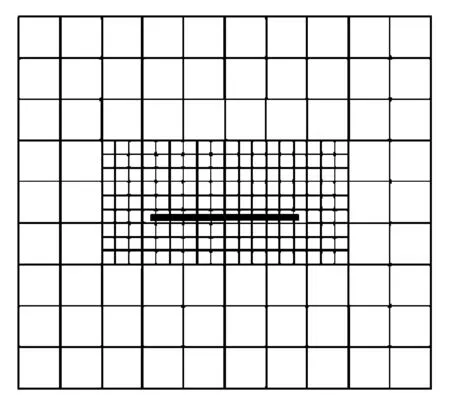
图2　多尺度网格(粗黑线为裂纹)

2多尺度扩展有限元法

2.1　四边形任意结点板单元

裂纹附近采用小尺度单元，其他区域采用大尺度单元。所有尺度均采用四边形四结点单元，则在不同尺度单元间存在一层四边形任意结点单元，如图2所示。下面给出四边形任意结点单元的形函数。

基于Np个多项式的点插值，用uh(ξ)逼近位移场u(ξ)，则uh(ξ)可表示为：

(8)

对于四结点四边形板单元，多项式基函数为：

p(ξ)=[1,ξ,η,ξη]T，

(9)

其中：ξ、η为等参元局部坐标。

由点插值可得：

uh(ξ)=aTp(ξ)=UTq-1p(ξ),

(10)

其中：

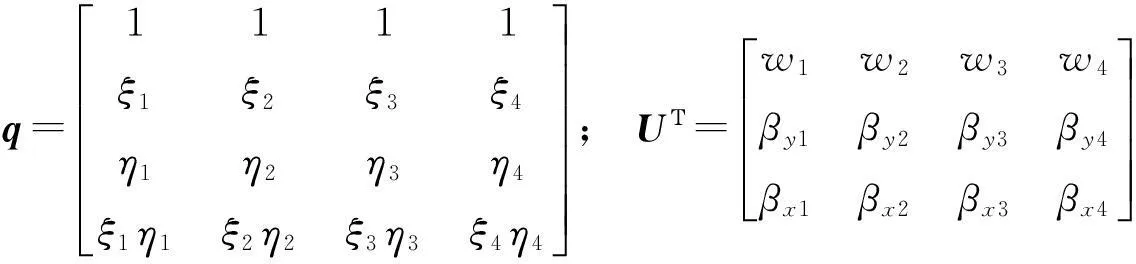
图3　四边形任意结点板单元

由式(8)～ 式(10)可得四结点四边形板单元形函数为：

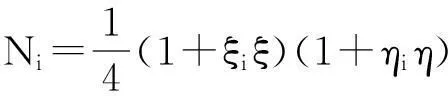
(11)

类似地，通过增加一些特殊的基函数以满足点插值，就可以得到四边形任意结点板单元的形函数。通过单元边上需要满足的插值类型来选取特殊的基函数。考虑一个线性的四边形任意结点板单元，称之为(4+k+m)结点单元，见图3。单元上的这些结点可以分为3类：第1类结点为4个角点；第2类结点有k个，位于四边形单元的上下两条边上；第3类结点有m个，位于四边形单元的左右两条边上。

多项式基函数可表示为[17]：

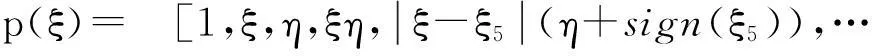
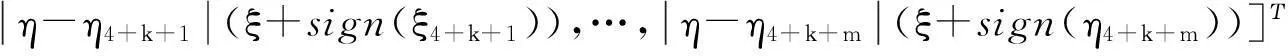
(12)

q=p(ξi)。

(13)

由式(10)可得，(4+k+m)结点单元的形函数为：

[N1,…,N4+k+m]T=q-1p(ξ)。

(14)

四边形任意结点板单元根据结点的不同会有很多种情况，而四结点四边形板单元只是众多情况中的一种，因此,单元的插值函数能够构造成同一种形式，这样有利于编程。并且四边形任意结点板单元上所有的结点,一定要是周围四结点四边形板单元的结点。

2.2　积分方案

为了保证充分积分应变场，采用如下的积分方案：(Ⅰ)四结点四边形板单元。该部分单元和常规扩展有限元单元的积分方案一样。(Ⅱ)四边形任意结点板单元。本文构造的四边形任意结点板单元的形函数在内部上出现不连续，而数值积分中是不允许出现不连续的，所以将单元划分成一些四结点四边形子单元，这些子单元的边是形函数斜坡不连续处。采用2×2个高斯积分点使每个子单元内形函数都是线性插值的。

3应力强度因子计算

采用互作用积分法[18]计算Reissner-Mindlin板的弯矩和剪力强度因子。

对于Ⅰ型和Ⅱ型应力强度因子，互作用积分为：

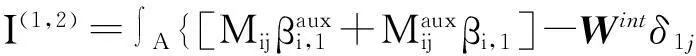
(15)

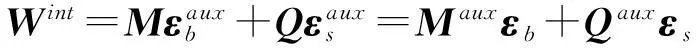
互作用积分与应力强度因子KI、KⅡ和KⅢ的关系为：

(16)

选取辅助状态为I型、II型或III型，根据式(16)就可分别求出 I型、II型或III型的应力强度因子。

4数值算例

图4　中心裂纹平板

算例1中心裂纹问题

含一中心裂纹的正方形平板(见图4)，板的两端受到弯矩M0的作用。板材料的弹性模量E=210 GPa，泊松比ν=0.3。板的尺寸L=20 m，裂纹长度为2a，板的厚度为t=2a，裂纹倾角为α。

无限大板含一中心斜裂纹的解析解为[19]：

(17)

其中：φ(1)和ψ(1)从积分方程中计算得来，当板的厚度t=2a时，φ(1)=0.82，ψ(1)=0.68。

图5为扩展有限元计算网格。首先，对整个区域采用大尺度单元进行离散，见图5a，称之为大尺度网格。然后，对裂纹附近单元进一步细化，本文将一个大单元细化为3×3的小单元，如图5b所示，称之为多尺度网格。为了便于比较，将所有单元都细化为3×3的小单元，如图5c所示，称之为小尺度网格。

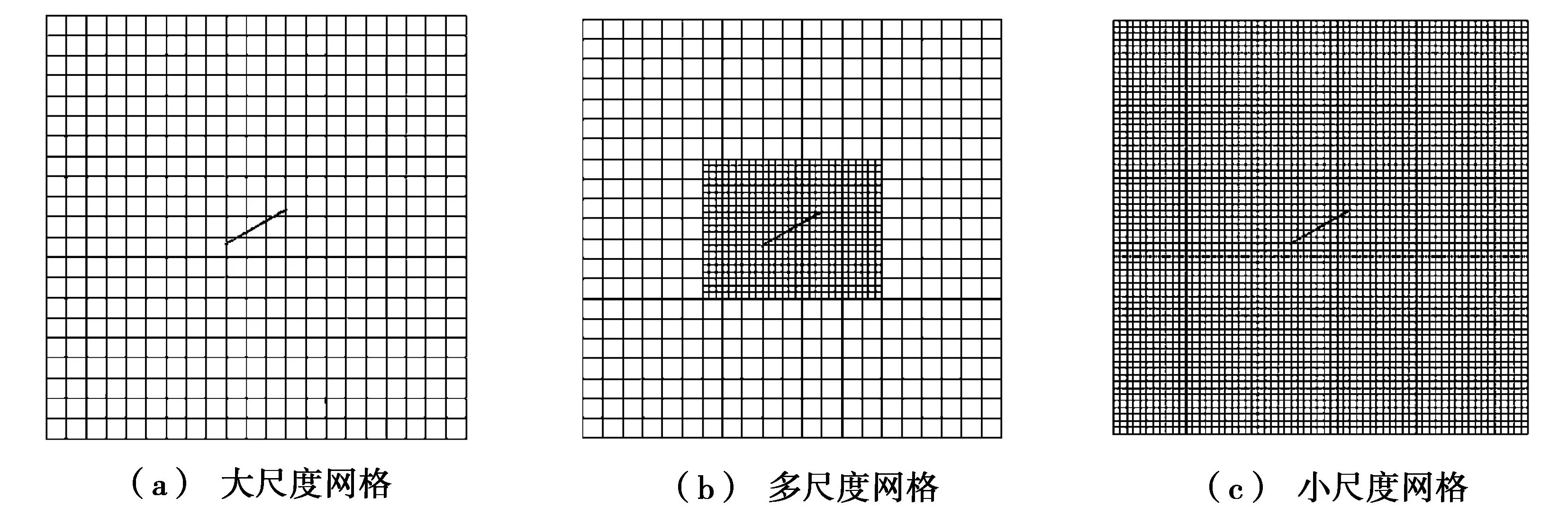
图5　扩展有限元计算网格

表1列出了不同类型网格下模型的自由度数目。由表1可知：多尺度问题的自由度要远小于小尺度问题的自由度。对于图5a，由于裂纹附近单元尺度太大，以致无法用互作用积分法计算应力强度因子。

裂纹附近存在高梯度应力，多尺度扩展有限元网格在裂纹附近采用了小尺度单元，因此，采用较少自由度网格的多尺度扩展有限元法就能获得较高精度的结果。多尺度扩展有限元法能大大节省计算量。

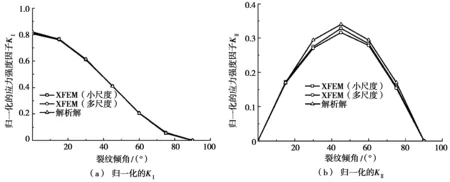
图6　应力强度因子随裂纹倾角的变化

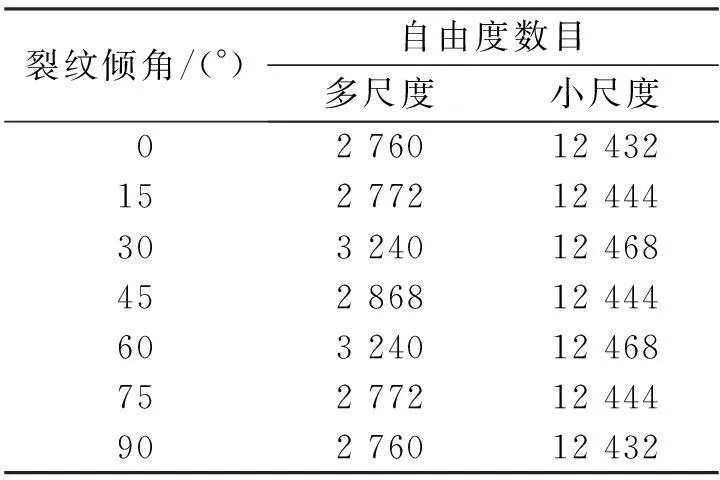
裂纹倾角/(°)自由度数目多尺度小尺度0276012432152772124443032401246845286812444603240124687527721244490276012432

算例2边裂纹问题

图7为含一边裂纹的长方形板，在板的两端受到弯矩M0的作用，板的高宽比c/b=2，宽厚比b/h=2，裂纹长度为a。板材料的弹性模量E=210 GPa，泊松比ν=0.3。

采用11×22个四结点四边形单元离散板，形成的网格称为大尺度网格。然后,对裂纹所在单元及外2层单元细化为3×3个单元，形成多尺度网格，如图8所示。将大尺度网格的每个单元细化为3×3个单元，形成的网格称为小尺度网格。

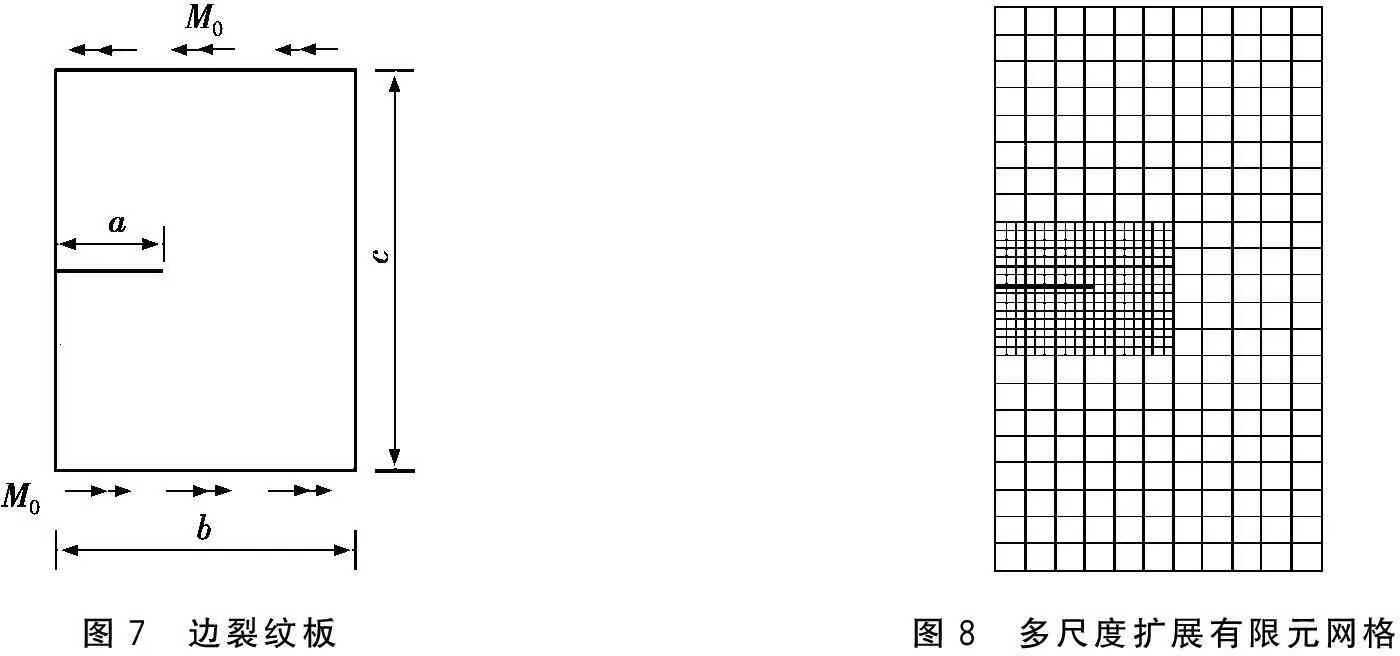
图7 边裂纹板图8 多尺度扩展有限元网格

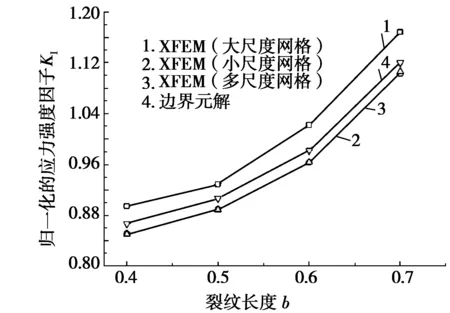
图9　归一化的KⅠ随裂纹长度的变化

5结论

(1)建立了Reissner-Mindlin板断裂问题的多尺度扩展有限元法，所有尺度单元都采用四结点四边形板单元，用四边形任意结点板单元来连接不同尺度单元。

(2)裂纹附近用小尺度单元进行划分，其他地方采用大尺度单元划分，这种多尺度扩展有限元法既能降低计算成本，又能得到较好的精度。

以后的工作将根据误差估计来科学地选取需要采用小尺度单元的区域，研究关于板断裂问题的自适应多尺度扩展有限元法。

参考文献：

[1]张振国,张娜,张秀丽,等.复合材料薄层板常温固化收缩及翘曲变形[J].河南科技大学学报(自然科学版),2009,30(6):1-5.

[2]BELYTSCHKOT,BLACKT.Elasticcrackgrowthinfiniteelementswithminimalremeshing[J].Internationaljournalfornumericalmethodsinengineering,1999,45(5):601-620.

[3]SUKUMARN,CHOPPDL,MORANB.Extendedfiniteelementmethodandfastmarchingmethodforthree-dimensionalfatiguecrackpropagation[J].Engineeringfracturemechanics,2003,70(1):29-48.

[4]YUTT,RENQW.Modelingcrackinviscoelasticmediausingtheextendedfiniteelement[J].ScienceChinatechnologicalsciences,2011,54(6):1599-1606.

[5]ASADPOUREA,MOHAMMADIS,VAFAIA.Modelingcrackinorthotropicmediausingacoupledfiniteelementandpartitionofunitymethods[J].Finiteelementsinanalysisanddesign,2006,42(13):1165-1175.

[6]LIUP,YUT,BUITQ,etal.Transientthermalshockfractureanalysisoffunctionallygradedpiezoelectricmaterialsbytheextendedfiniteelementmethod[J].Internationaljournalofsolidsandstructures,2014,51(11):2167-2182.

[7]SUKUMARN,CHOPPDL,MOЁSN,etal.Modelingholesandinclusionsbylevelsetsintheextendedfinite-elementmethod[J].Computermethodsinappliedmechanicsandengineering,2001,190(46):6183-6200.

[8]SAMANIEGOE,BELYTSCHKOT.Continuum-discontinuummodellingofshearbands[J].Internationaljournalfornumericalmethodsinengineering,2005,62(13):1857-1872.

[9]SIAVELISM,GUITONMLE,MASSINP,etal.LargeslidingcontactalongbrancheddiscontinuitieswithX-FEM[J].Computationalmechanics,2013,52(1):201-219.

[10]CHESSA J,BELYTSCHKO T.An enriched finite element method and level sets for axisymmetric two-phase flow with surface tension[J].International journal for numerical methods in engineering,2003,58(13):2041-2064.

[11]HOLL M,LOEHNERT S,WRIGGERS P.An adaptive multiscale method for crack propagation and crack coalescence[J].International journal for numerical methods in engineering,2013,93(1):23-51.

[12]NEMAT-NASSER S,HORI M.Micromechanics:overall properties of heterogeneous materials[M].Amsterdam:North-Holland,1999.

[14]RANNOU J,GRAVOUIL A,BAÏETTO-DUBOURG M C.A local multigrid XFEM strategy for 3D crack propagation[J].International journal for numerical methods in engineering,2009,77(4):581-600.

[15]HOLL M,ROGGE T,LOEHNERT S,et al.3D Multiscale crack propagation using the XFEM applied to a gas turbine blade[J].Computational mechanics,2014,53(1):173-188.

[16]王振,余天堂.模拟三维裂纹问题的多尺度扩展有限元法[J].岩土力学,2014,35(9):2702-2707.

[17]SOHN D,IM S.Variable-node plate and shell elements with assumed natural strain and smoothed integration methods for nonmatching meshes[J].Computational mechanics,2013,51(6):927-948.

[18]DOLBOW J,MOЁS N,BELYTSCHKO T.Modeling fracture in Mindlin-Reissner plates with the extended finite element method[J].International journal of solids and structures,2000,37(48):7161-7183.

[19]SIH G.Mechanics of fracture 3:plates and shells with cracks[M].The Netherlands:Noordhoff,1977.

[20]DIRGANTARA T,ALIABADI M H.Stress intensity factors for cracks in thin plates[J].Engineering fracture mechanics,2002,69(13):1465-1486.

文献标志码：A

中图分类号：TU311;P315.9

DOI:10.15926/j.cnki.issn1672-6871.2016.02.003

文章编号：1672-6871(2016)02-0011-06

收稿日期：2015-10-20

作者简介：胡凯(1989-),男,湖北黄冈人,硕士生，主要从事计算力学与工程仿真方面的研究.

基金项目：国家自然科学基金项目(51179063)