基于模糊数学的健美操CAI课件综合评价

Comprehensive Evaluation of Aerobics CAI

Courseware on the Basis of Fuzzy Mathematics

袁桂才，孙　浩

Yuan Guicai, Sun Hao

基于模糊数学的健美操CAI课件综合评价

Comprehensive Evaluation of Aerobics CAI

Courseware on the Basis of Fuzzy Mathematics

袁桂才，孙浩

Yuan Guicai, Sun Hao

作者单位：金陵科技学院基础部，江苏 南京211169

1模糊数和教学评估

在上个世纪后期，世界上很多数学家对模糊数学理论进行了彻底的研究。著名的模糊科学家，比如A. Kaufman，E. SanchZ，YoKo，以及一个名为PPZ的美籍华裔，在这一领域做出了杰出的贡献，他们来到中国推广他们对模糊数学的理解。这些前辈在模糊数学领域创造了历史。在1976年，中国数学家开始投身于模糊数学的研究，并对模糊理论及其在中国的应用做出了巨大的贡献。模糊集与系统协会成立于1980年，模糊数学杂志创立于1981年，这标志着在这个领域的重大进步[3]。同时，国内数学家发表了大量的著作。其中陈水利教授著作了《模糊集理论及其应用》，张国立教授编写了《模糊数学基础》，他们是这些数学家的杰出代表。在近几年，中国和美国、西欧和日本[4]并称世界四大著名模糊数学研究中心。

就模糊数学的应用和课件而言，中国的许多学者已经对此进行了广泛的讨论。Peng使用模糊数学进行综合分析，根据大学生的特点，作者选择了六个素质指标，包括思想、政治和道德素质，来评价运动员的综合素质，将素质划分成五个等级[5]。另外，Peng构建了基于综合评价的模糊数学模型，在案例计算之后，他通过比较验证了评价体系的可靠性，并指出了模糊数学在课件质量评价中的优点。根据模糊综合评价方法，Peng评价了电脑基础课程的教学质量，并获得了三层次模糊综合评价模型[6]。这个实验性测试显示了这个程序是简单可行的。针对当前单目标跟踪数据融合中存在的迭代求解计算量大，难以满足实时计算要求的问题，潘昶[7]提出了一种将模糊数学和非负特征向量理论相结合的数据融合算法。该方法克服了卡尔曼滤波法、最小二乘法需要建立统一的测量方程，进行迭代求解、计算量大的问题。与传统方法相比，该方法能充分利用测量数据，提高目标跟踪精度，计算简便，便于工程实现。这些学者的讨论有些结果，但是很少有学者对健美操多媒体课件进行质量评估。

理论的发展不可避免地推动了应用。模糊数学随之在很多领域获得了广泛的应用，比如工业、农业、生物、化学、金融和经济。另外，它现在扮演着越来越重要的角色。

在健美操教学中，大多数教师采用相对简单的教学形式，学生在学习的过程中会感到无聊和厌烦。于是，学生对课程就不热衷，教师也无法达到教学的目的。在此大环境下，随着计算机和网络的发展和普及，一些人建议使用Photoshop，Power point和其他软件来创造CAI课件以支持学习和教学，即是用各种生动的形式展示教学内容，比如文本、图片、影像、动画等，使得学生更轻松、更愉快、更全面地从不同角度理解健美操的动作，并提高学生的学习效率以及教师的教学质量。

相对于传统的健美操教学，健美操CAI课件毫无疑问拥有很多优点。首先，它帮助学生清楚地抓住教学要点。其次，它减轻了教师的负担。

但是，制作这样的CAI课件对健美操教师的素质提出了很高的要求，因为他们必须熟练掌握计算机知识。同时，它对教学设施和场地也有要求。这不可避免地大幅度增加了健美操教学成本。从经济的角度来看，我们应以某种方式量化健美操CAI课件的好处，以便人们对在教学中使用健美操CAI课件做出一个合理的评价。在本文中，基于模糊数学的综合评价方法被用于对其进行测量。

2模糊数学和基于模糊数学的综合评价

2.1　模糊数学理论的定义

模糊数学于1965年由美国计算机和控制论专家LAZadeh提出，模糊数学是康托集合论的发展，它是一种研究和处理模糊现象的一种数学理论和方法。这个新发展有实际的重要意义。在经典集合理论中，一个元素要么属于一个集合，要么不属于一个集合。但是，一些事物之间的关系是模糊的，它们并不能简单地归于上述两类。相应地，使用模糊数学来考察它们更精确。

2.2　模糊数学理论相对于传统集合理论的优越性

模糊数学理论、随机理论和不确定理论构成了两个事物之间关系的理论基础。在这三个理论中，模糊数学更多地强调分辨莫以实物是否有一定程度的某一特性，而不是要求非常复杂的科学计算，即，模糊数学更多地强调相似性而不是相同性。正是模糊数学的上诉独特性和优越性，在实际生产和生活中，用模糊数学来解决许多实际问题更合理。例如，在生物学和医学中，可以使用模糊数学来处理指纹信息，可以又快又好地解决问题。

2.3　基于模糊数学的综合评价方法

2.3.1模糊综合评价的定义

根据已确立的标准，单一评价是对某一因素或某类因素或某一部分进行评价，综合评价被视为通过单一评价对某一事物或某类事物进行整体评价。在实际操作中，被评价的事物通常有很多不确定性。因此，要将学生对健美操CAI课件评价中展示的模糊性考虑进去，包括课件版面布局、排版合理性、动画、图像、清晰度、声音回放速率、字体大小、颜色和风格、背景颜色和图案选择等。在这种情况下，使用模糊综合评价方法将会使得结果更客观。

2.3.2单层次模糊综合评价法模型

要评价一件事物的优劣，我们必须从它的各种性质开始入手，即所谓的各种“因素”，因为这些各种各样的因素能够反映出我们要评价的事物的实质。

我们将集合U = {u1, u2,......un} 设为综合评价的因素所组成的集合。

我们用集合V = {v1, v2,......vm} 来表示评语所组成的集合。

为了要使用模糊综合评价法，我们首先建立一个单个的因素评价，这个单个的因素评价即是一个从U到V的模糊映射: γ: U → F (V )。

第i个单个因素的评价为 γ (u ) = γ (ui)(v1) + γ (ui)(v2) + ....... + γ (ui)(vm)。 其中γ(ui)(vj)( j = 1......m) 表示第i个单个因素的评语(评价内容)为j的评价。为了要从一个单个因素的评价结果中得到综合评价结果，我们需要建立一个函数 f :[0,1]n→[0,1]。来让每个分开独立的因素聚合在一起。为了理论和实际操作上的需要，这个函数应该是满足以下这些性质的：

(1) 规整性： 如果 x1= x2= ...... = xn= x成立，那么 f ( x1, x2,......xn1) = x 成立。

(2) 单调性： 对任意一个i, 如果 xi (1) ≤ xi ( 2) 成立，那么

f(x1,......xi-1,xi(1),xi+1,......xn)≤f(x1,......xi-1,xi(2),xi+1,......,xn)

(1)

(3) 连续性：f ( x1, x2,......xn1) 对所有变量是连续的

一旦f ( x1, x2,......xn1) 符合上述条件，那么

(f(γ(u1)(v1),γ(u2)(v2),......γ(un)(v1)),

f(γ(u1)(v2),γ(u2)(v2),......γ(un)(v2)),......

(2)

f(γ(u1)(vm),γ(u2)(vm),......γ(un)(vm)))

这就是U的综合评价。

这里列出几种常见的综合评定法。

① 权重分配类型

假设

② 单个因素的决策属性

假设

③ 几何意义类型

假设

④ 主要突出因素类型

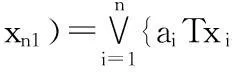
2.3.3多层次模糊综合评价法模型：

(1) 把元素集合 U = {u1, u2,......un} 根据特定属性划分为 r s 不重叠的层级：

Ui={ui1,ui2,......uin},i=1,2,......s

(3)

其中

(2) 发散集合V={v1,v2,......vp}.

(3) 建立元素型权重向量，如果第i级因素权重为 ai那么 A = (a1, a2,...., as) 为元素型权向量。

建立元素型权向量，假设第i级的第j个元素的权重为 aij那么 Ai = (ai1, ai 2,...., ain) 为元素型权向量。

(4) 在第一层级的综合评定中，对各层级中的各因素进行综合评价。

(4)

那么第i层级的综合评价为：Bi=Ai○TRi

(5) 第二层级综合评价

(5)

那么第二层级的综合评价为：B=A○TR

(6) 多层次评价

对于任意子集Ui中的第nk个元素，根据单层次模糊综合评价法模型来进行评价。如果子集Ui中的元素的权重分配为Ai，那么起决定性作用的矩阵为Ri，且我们能够得到第i个子集Ui的综合评价结果： Ui:Bi=Ai×Ri=[bi1,bi2,......,bin]

对 Ui(i = 1,2, ..., m) 子集的m元素进行评价，那么评价的决定性矩阵如下：

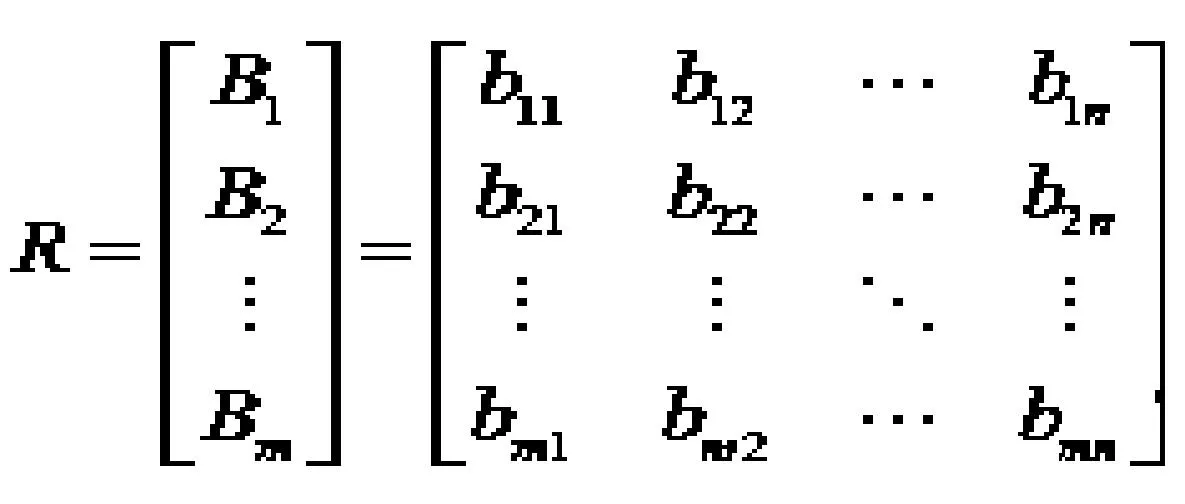
(6)

如果集合U的子集中的元素的权重分配为A，那么我们能得到如下的综合评价结果：B=A×R

(7)

其中

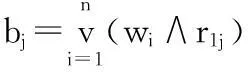
(8)

进行B的归一化过程于是我们可以得到 B*=(b1*,b2*,......,bn*)。在 B* 等式中：

B=A×R=[b1,b2,......,bn]

3通过模糊数学理论的综合评价方法对健美操计算机辅助教学软件进行评价。

在对健美操计算机辅助教学的评价过程中，几个主要的影响因素包括界面布局和整合的合理性、界面的美观、界面的显著颜色、字体大小、字体颜色、字体形状、字体清晰度以及动画效果的流畅性和操控性、背景颜色和背景式样。从统计科学的角度来看，我们采用了统计采样调查的理念，并且随机开展了一次面对300名武汉体育学院选修健美操课的问卷调查。

3.1　因素分类及因素权重的选取。

表1　元素层次权重及权重值表

3.2　建立模糊评价集合

创建评价分数段，分为非常好、好、一般、差、非常差这几个区段。于是评价集合为 V = {v1, v2,......vm} = {非常好，好，一般，差}

3.3　多层次模糊综合评价

根据上面所设计的分类和权重分配分发300份问卷。经监督及核查，有效问卷的数量为240份。问卷的调查结果总结在下方的表2中。

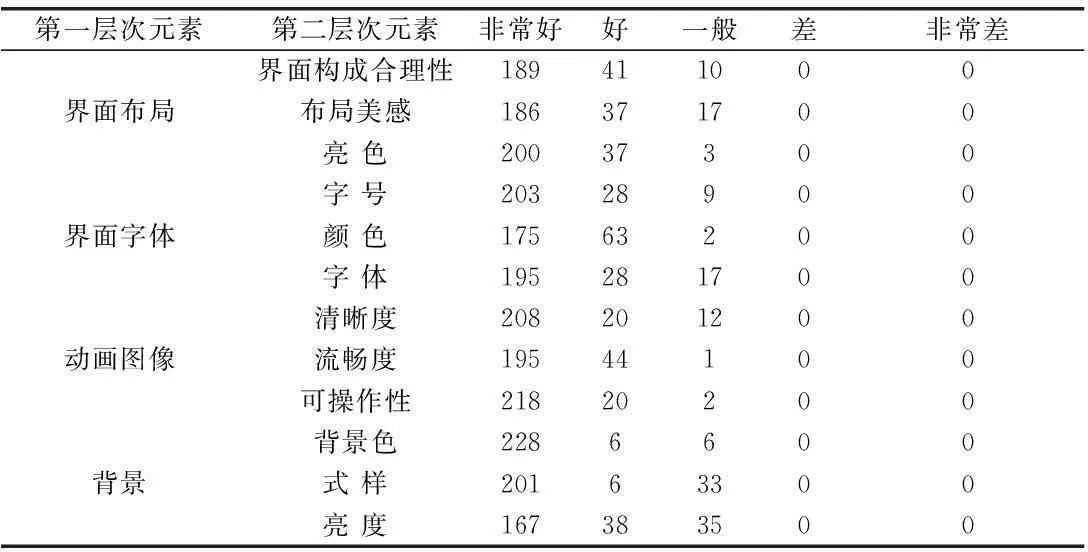
表2　有效问卷调查结果汇总表

首先，按照如下方式进行第一层次综合评价:

举界面布局设计作例子：

[0.7960.1670.0500]

依此，我们可以得到字体的评价结果

B2=[0.7840.1610.05400]

动画图像评价的结果为

B3=[0.8580.1170.0170.0080]

背景评价的结果为

B4=[0.850.050.100]

根据运算结果，健美操计算机辅助教学软件在四个范畴(非常好、好、一般、非常差)的隶属程度分别为82.5%, 12.3%, 5.4%, 0.2% 和 0%。

4结果分析

根据用上述模糊方法计算出的结果以及根据健美操计算机辅助教学软件的总体质量调查，我们能够获知，班级里大部分的学生对于软件的界面布局、字体、动画图像及背景比较满意。满意程度超过了80%，到达了“好”的层次。几乎没有学生认为健美操计算机辅助教学软件差或非常差。高品质的健美操计算机辅助教学软件无疑在提升课堂趣味、提高学生学习效率以及教师教学质量的方面很有作用。可见，这种高科技的教学方式应该被更加广泛地普及。

5研究存在的问题及前景。

根据引索系统以及模糊数学方法的发展进程和要求，本文相应地提供了多媒体教学软件评价引索系统并且保证了学术研究结果的合理性以及可靠性。然而，由于现实条件的制约，仍有许多不完美的地方。研究中最主要的问题如下所述:

1.在专家意见方面，由于客观因素影响如时间约束等，要充分且透彻地咨询相关的专家学者非常不容易。

2.至于健美操教学软件的采样数量，存在一些实际操作的问题，例如大范围的教学软件在国内体育运动机构。因此，完整地收集采样是很困难的。另外，研究涉及的多为相对而言同种类的教学软件，并且采样的数量比正常数量要少。

3.有一些体育教育机构应该开展教学软件资源的交流和共享。这些机构应该增强与不同学校之间的学术交流，减少人力、财务和物质资源，为建立专业的教学数据库做出做贡献，并且应努力在有限的教育投资情况下获得最大的教学成效。

参考文献：

[1]张国立.模糊数学基础及应用[M].北京：化学工业出版社，2011.

[2]陈水利.模糊集理论及其应用[M].北京：科学出版社，2005.

[3]祖苇.普通高校健美操CAI课件研制的尝试与探讨[J]，山西师大体育学院学报，2003，( 9 )：25-27.

[4]潘昶，张德全.于模糊数学的数据融合算法研究[J]，指挥控制与仿真，2009，( 2 )：65-69.

Basic Department, Jinling Institute of Technology, Nanjing 211169, Jiangsu, China.

摘要：在经典康托集的基础上，派生出了一个数学分支-模糊数学。因此，对事物之间的关系的研究就不仅包括不确定关系和随机关系，还包括模糊关系。随着数学家越来越多地关注这个研究领域，模糊数学的理论日益完善。模糊数学已经被广泛用于解决实际问题。近年来，为了增加对健美操课程的兴趣以及健美操教学的有效性和可操作性，越来越多的大学已经采用了健美操CAI课件。同时，现代科技的进步和计算机知识的普及已经使得通过电子设施实施教学成为可能。本文详细探讨了模糊数学相对于传统康托集的优越性并解释了单层次和多层次模糊数学的概念和具体操作过程。基于武汉体育学院体操班随机抽样调查的有效数据，本文采用模糊数学综合评价来理性地辨别教学方法的合理性和优越性。

关键词：模糊数学；综合评价；健美操CAI课件

Abstract:On the basis of classical Cantor sets, there derives a branch of mathematics, the fuzzy mathematics. Therefore, the study of the relationship between things includes not only uncertainty and random relations, but also fuzzy relation. With mathematicians paying more and more attention to this research field, the theory of fuzzy mathematics is becoming more and more perfect. Fuzzy mathematics has been widely used in solving practical problems. In recent years, in order to increase the interest in aerobics curriculum and the effectiveness and operability of aerobics teaching, a growing number of colleges have adopted aerobics CAI courseware. At the same time, the progress of modern science and technology and the popularity of computer knowledge have made it possible to teach through electronic facilities. The paper goes into a detailed exploration of the advantage of fuzzy mathematics over traditional Cantor set and explains concept and concrete operation process of sheer level and multi-level fuzzy mathematics. Based on the effective data of random sampling of Wuhan Sports University gymnastics class, this paper adopts fuzzy mathematics comprehensive evaluation to rationally recognize the rationality and superiority of teaching method.

Key words:fuzzy mathematics; comprehensive evaluation; aerobics CAI courseware

doi:10.3969/ j.issn.1005-0256.2016.01.030

中图分类号：G835

文献标识码：A

文章编号：1005-0256(2016)01-0067-4

作者简介：第一袁桂才(1979-)，男，江苏南京人， 副教授，硕士，研究方向：体育教育与运动训练。