七参数坐标转换中一种削弱高程误差影响的新方法

2016-02-26刘邢巍

测绘通报 2016年1期

关键词：坐标转换新方法高程

赵　文，刘邢巍，袁　鹏

(1. 武汉大学测绘学院，湖北武汉 430079； 2. 武汉大学卫星导航定位技术研究中心，湖北武汉 430079)

A New Solution to Weaken Influence of Ellipsoidal Height

Error on Seven-parameter Transformation

ZHAO Wen,LIU Xingwei,YUAN Peng

七参数坐标转换中一种削弱高程误差影响的新方法

赵文1，刘邢巍1，袁鹏2

(1. 武汉大学测绘学院，湖北武汉 430079； 2. 武汉大学卫星导航定位技术研究中心，湖北武汉 430079)

A New Solution to Weaken Influence of Ellipsoidal Height

Error on Seven-parameter Transformation

ZHAO Wen,LIU Xingwei,YUAN Peng

摘要：在较大区域中，利用七参数法实现二维坐标至三维坐标转换时，高程精度影响坐标转换精度。本文提出了一种新方法，可解决七参数坐标转换中高程精度影响平面坐标精度的问题。该方法在无高程情况下，对4°×8°的大区域可实现1 cm左右的转换精度。同时，通过真实测量数据和模拟数据阐明了新方法的可行性和适用范围。

关键词：七参数；高程；坐标转换；CGCS2000；新方法

当前，2000国家大地坐标系(China geodetic coordinate system 2000，CGCS2000)已经正式启用。此前，我国测绘成果广泛采用的坐标系统为1954北京坐标系(简称BJ54)和1980西安坐标系(简称XA80)，二者均为平面坐标系。实现BJ54、XA80与CGCS2000间平面坐标转换，可采用平面四参数转换模型和七参数空间转换模型。由于平面转换模型是一个线性模型，高斯投影变形误差不能顾及，因而较多采用空间转换模型[1]。我国高程系统与平面坐标系统分离，且采用正常高，已知平面坐标的点只有水准高程，或没有任何高程(大地高、正常高、正高等)信息。文献[1]从理论上研究表明：对于地面上100 km×100 km的范围，即使公共点中地方坐标的高程存在误差，七参数法转换出来点的平面坐标仍基本不变。但该理论是否适用于较大区域范围或公共点高程未知的情形，该文献并未进行研究。本文探讨了区域范围较大或点高程未知情况下，高程精度对七参数法转换出来点的平面坐标精度的影响，并提出了一种新方法，以解决七参数坐标转换中高程精度影响平面坐标精度的问题，最后结合真实数据和模拟数据验证了新方法的可行性和适用范围。

一、坐标转换方法

1. 常用方法

常用方法流程如图1所示。

图1　常用方法流程

其具体步骤如下：

2. 新方法

图2　新方法流程

具体步骤为：

5) 按照上节“常用方法”中的步骤4)和步骤5)计算。

二、算例分析

1. 真实数据分析

本文选取位于我国中部某地区，纬度和经度跨度约为4°×7.5°内的165个公共点作为区域1，选取位于我国华南某地区，纬度和经度跨度约1.5°×1.5°内的226个点作为区域2。公共点具有BJ54坐标系和CGCS2000坐标，其中公共点在BJ54坐标系下的坐标形式为高斯平面坐标，无高程信息，在CGCS2000下的坐标形式为空间直角坐标。对两组数据均每10个数据点中选取1个点作为检核点，并分别采用常用方法与新方法进行坐标转换。其点位分布分别如图3和图4所示。

图3　区域1的点位分布

图4　区域2的点位分布

坐标转换结果见表1—表4。

表1　区域1的内符合精度　m

表2　区域1的外符合精度　m

表3　区域2的内符合精度　m

表4　区域2的外符合精度　m

对于大区域，从表1、表2数据分析可得，新方法x、y方向的标准差在1 cm左右，而常用方法x、y方向的标准差超过3.0 m；新方法x、y方向上的残差最大值均优于5.0 cm，常用方法x、y方向上的残差最大值均超过6.0 m。分别以标准5.0 cm和1.0 cm来统计残差信息：在x方向上，常用方法所有残差基本均超过1.0 cm，且80%以上的残差超过5.0 cm，而新方法79%以上的残差优于1.0 cm，且所有残差均优于5.0 cm；在y方向上，常用方法所有残差均超过5.0 cm，而新方法70%以上的残差优于1.0 cm，且所有残差均优于5.0 cm。

对于小区域，从表3、表4数据分析可得，新方法x、y方向的标准差均基本为0.0 m,而常用方法x、y方向的标准差均超过0.2 m；新方法x、y方向的残差最大值均优于5 mm，而常用方法x、y方向的残差最大值均超过0.4 m。分别以标准0.5 cm和0.1 cm来统计残差信息：在x方向上，常用方法所有残差均超过5 mm，而新方法70%以上的残差优于1 mm，且所有残差均优于5 mm；在y方向上，常用方法92%以上的残差超过5 mm，97%以上的残差超过1 mm，而新方法有45%以上的残差优于1 mm，且所有残差均优于5 mm。

从表1—表4中数据分析可知，不论是实现大区域的平面坐标转换，还是实现小区域的平面坐标转换，采用新方法时，其坐标转换精度均明显高于常用方法，并且实现小区域的坐标转换精度明显优于大区域。由于BJ54高程信息未知，故将点位高程统一作为0进行处理，此时高程精度很差，其对平面坐标的转换精度的影响很大，不可忽视。若采用常用方法实现坐标转换，转换后的坐标精度严重不足。而采用本文提出的新办法可以较好地解决BJ54高程信息未知而带来的高程精度问题，实现较高精度的平面坐标转换。对于1.5°×1.5°的区域范围，坐标转换后，新方法在x、y方向上的精度可达2 mm，均优于1 cm；对于4°×8°的区域范围，坐标转换后，新方法在x、y方向上的精度也可达1 cm左右。

为了进一步验证上述结论，本文采用模拟数据来进行进一步分析。

2. 模拟数据分析

其中，选取1、4、7、10四个点作为检核点(即表中带*号的点)，模拟数据点位分布如图5所示。

坐标转换结果见表6。

表5　模拟点位在CGCS2000下的坐标

图5　模拟点位的分布

注：表中带*号的点为检核点，其余点均为参与解算点。

结合表6中数据，对常用方法、新方法分别实现模拟数据坐标转换的结果进行分析：

1) 内符合检核。常用方法在x、y方向上的坐标残差绝对值均很大，其中x方向上的残差绝对值最小为3.846 m，位于12号点，y方向的残差绝对值最小为0.499 m，位于6号点；而新方法在x、y方向上的残差绝对值均优于1.0 cm，其中，x方向的残差绝对值最大为0.006 m，位于2号点，y方向的残差绝对值最大为0.006 m，位于3号点。在内符合精度上，新方法明显优于常用方法。

2) 外符合检核。常用方法在x、y方向上的坐标残差绝对值也很大，其中x方向的残差绝对值最小达到2.861 m，位于7号点，y方向的残差绝对值最小达到9.717 m，位于7号点；而新方法在x、y方向上的残差绝对值均优于1.0 cm，其中，x方向的残差绝对值最大为0.006 m，位于1号点，y方向的残差绝对值最大为0.009 m，位于1、4号点。在外符合精度上，新方法亦明显优于常用方法。

通过模拟数据分析可得，新方法在内、外符合精度上均明显优于常用方法。对于4°×8°的模拟区域范围，在x、y方向上，新方法与高程迭代法生成的模拟真实值间差异优于1.0 cm。文献[4]研究表明：当经纬度的跨度范围均小于8°时，高程趋近法x或y方向的坐标差值均在1 cm左右。下面通过误差传播定律推算新方法的转换精度

(1)

式中，Δx1=x真实-x高程迭代；Δx2=x高程迭代-x新方法；Δy1=y真实-y高程迭代；Δy2=y高程迭代-y新方法。已知σΔx1=σΔx2=σΔy1=σΔy2≈1.0 cm，则由式(1)利用误差传播定律得

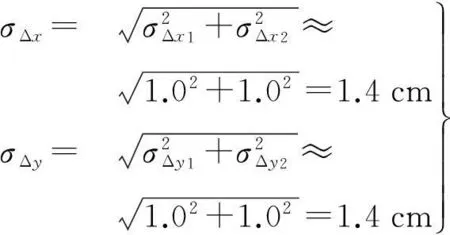
(2)

即对于4°×8°的区域范围，新方法可以实现在x、y方向上1.4 cm左右的坐标转换精度，与真实数据的转换精度1.0 cm左右较为吻合。

三、结束语

当BJ54和XA80坐标系下点位高程未知时，若

采用常用方法进行坐标转换，高程精度对坐标转换精度影响很大，不可忽视。而本文提出的将其高程统一为0进行转换的新方法，无须提供BJ54和XA80坐标系下点位高程，对于4°×8°的大区域，在平面x、y方向上坐标转换精度均为1 cm左右，明显优于常用方法，较好地解决了高程精度差带来的问题。该方法可以实现大区域现行坐标系下的测绘成果向CGCS2000的高精度平面坐标转化，具有很高的实用价值。

参考文献：

[1]王解先，邱阳媛.高程误差对七参数转换的影响[J].大地测量与地球动力学,2007,27(3):25-27.

[2]王解先，王军，陆彩萍.WGS-84与北京54坐标的转换问题[J].大地测量与地球动力学,2003,23(3):70-73.

[3]王解先.七参数转换中参数之间的相关性[J].大地测量与地球动力学,2007,27(2):43-46.

[4]谢鸣宇，姚宜斌.三维空间与二维空间七参数转换参数求解新方法[J].大地测量与地球动力学,2008,28(2):104-109.

[5]成英燕，程鹏飞，秘金钟，等.大尺度空间域下1980西安坐标系与WGS-84坐标系转换方法研究[J].测绘通报,2007(12):5-8.

[6]成英燕，李夕银.适用于不同椭球的高斯平面坐标正反算的实用算法[J].测绘科学,2004,29(4):26-27.

[7]顾旦生.一组高精度椭球面电子计算实用公式[J].测绘通报,1997(3)：2-9.

[8]施一民,冯琰.两种测地坐标系之间的坐标转换[J].测绘学报,2002,31(5)：22-26.

[9]孔祥元，郭际明.大地测量学基础[M].武汉:武汉大学出版社，2005.

[10]李征航，魏二虎.空间大地测量学[M].武汉:武汉大学出版社，2010.

引文格式：赵文，刘邢巍，袁鹏. 七参数坐标转换中一种削弱高程误差影响的新方法[J].测绘通报，2016(1)：11-14.DOI:10.13474/j.cnki.11-2246.2016.0003.