公里格网约束下的大区域平面坐标快速转换模型研究

2016-02-26何桂芳杨军生刘民士钟文军

测绘通报 2016年1期

关键词：图幅格网控制点

何桂芳，杨军生，刘民士，钟文军

(1. 滁州学院地理信息与旅游学院，安徽滁州 239000； 2. 安徽省地理信息集成应用协同创新中心，

安徽滁州 239000； 3. 宁波东钱湖旅游渡假区规划管理中心，浙江宁波 315121；

4. 宁波规划院地理信息中心，浙江宁波 315041)

Research on Regional Plane Coordinate Rapid Transformation Model

under Kilometer Grid Constrains

HE Guifang，YANG Junsheng，LIU Minshi，ZHONG Wenjun

公里格网约束下的大区域平面坐标快速转换模型研究

何桂芳1,2，杨军生3，刘民士1,2，钟文军4

(1. 滁州学院地理信息与旅游学院，安徽滁州 239000； 2. 安徽省地理信息集成应用协同创新中心，

安徽滁州 239000； 3. 宁波东钱湖旅游渡假区规划管理中心，浙江宁波 315121；

4. 宁波规划院地理信息中心，浙江宁波 315041)

Research on Regional Plane Coordinate Rapid Transformation Model

under Kilometer Grid Constrains

HE Guifang，YANG Junsheng，LIU Minshi，ZHONG Wenjun

摘要：提出了以公里格网为约束，以区域面积为加权因子的逐格网纠正技术的大区域平面坐标快速转换模型。该模型首先在待转换数据上布设公里格网，建立公里格网与待转数据间的关系，然后以格网控制点为基准数据，通过区域面积加权求解的方法对待转数据进行逐格网坐标转换。通过安徽省域范围内1954北京坐标系到CGCS2000平面坐标转换试验表明，该模型在保证转换精度的条件下，避免了大区域平面坐标转换过程中分幅或分区转换，具有较好的实用性。

关键词：2000国家大地坐标系；1954北京坐标系；1980西安坐标系；平面坐标；坐标转换

国家测绘地理信息局规定从2008年7月1日起，其他仍在使用的坐标系统(如1954北京坐标系、1980西安坐标系)都要向CGCS2000坐标系转换[1-2]。事实上，由于当前丰富多样的空间数据中包含着多种的坐标系统，实际应用中经常面临纷杂的坐标转换，空间数据的坐标转换(尤其是平面坐标的转换)已成为GIS空间数据共享、空间数据集成建库、空间分析应用等过程中经常发生的基本操作[3-4]。空间数据的平面坐标系统转换方法研究得到了众多学者的高度关注，目前研究建立的平面坐标转换方法主要包括解析变换和非解析变换。

解析变换直接对平面坐标系进行大地坐标系到投影坐标系的正解和反解得出，优点是计算结果精度高，缺点是模型复杂，需要参数多，更为重要的是两个坐标系统之间必须要存在严密的数学解析关系。因此，更多的研究集中在非解析变化转换模型，主要有4种模型方法：①大地坐标解算方法[5-7]，其先计算两个坐标系下的大地坐标差值，然后通过投影变换计算平面坐标差值，最后加上两个系统间的平差改正数得到最终坐标改正量。该方法计算复杂，计算量大，而实际操作中以基准点的坐标改正量代替一个图幅，因而仅适用于单个图幅，并不适用于大区域的空间数据集成建库。②多项式模型方法[8-9]，该方法通过构建一个多项式模型，通常采用一个高阶曲面来模拟两个空间坐标系的变换关系，根据控制点拟合解出模型参数，其困难之处在于难确定与真实模型一致的多项式模型或阶数，此外该方法还会带来数据的扭曲变形。③相似转换模型方法[10-11]，具体包括三维七参数、二维七参数、平面四参数等模型，是通过平移、旋转、比例变换参数来构建两个空间直角坐标系或平面坐标系的转换模型。该方法能较精确地表达两个坐标系之间的转换，但当区域较大时，拟合的精度有限。④仿射变换模型方法[12]，仿射变换模型方法是直接针对平面坐标系之间转换的一种方法，其实质是建立两个平面坐标系之间的线性模型，近似于平面四参数模型，但其方法更为简单、易于计算，不足之处在于其转换精度仅能保证较小区域，区域较大，不能保证变换精度。

根据国家测绘地理信息局对坐标转换精度的要求规定，小于或等于1∶5万比例尺空间数据的单个图幅采用以上方法是能够达到要求的精度，而对于大于1∶5万比例尺的空间数据，单个图幅采用相同的转换参数不能满足其精度要求，因此要对单个图幅先进行分区，再计算分区转换参数[13]，这就导致了分区间要进行图幅拼接(如图1所示)；另外，针对大区域数据，必然面对多个图幅，即便单个图幅采用同一转换参数，不同图幅间也要进行图幅拼接。

图1　平面坐标分幅转换示意图

综上所述，大区域平面坐标快速转换存在问题如下：一是没有很好的模型；二是采用分幅或分区转换时不可避免地存在相邻图幅二次接边过程，效率低且容易引入人为错误，值得深入研究。基于此，本文提出一种以公里网为约束，以区域面积为加权因子的逐格网纠正技术的大区域平面坐标快速转换模型。该转换模型既能满足坐标转换的精度，同时还避免了大区域的分幅或分区转换。

一、公里网约束的平面坐标转换算法

基于公里网约束的平面坐标转换基本思想为：首先将待转换的数据按照高斯-克吕格带布设公里格网(如图2(a)所示)，建立待转换数据与公里格网间的关系，再通过公里格网约束对待转换数据进行逐公里格网纠正，只要待转换数据范围在一个高斯-克吕格条带内，就可直接转换，而无须分幅转换。具体来说，对位于公里格网内各个数据点，以该点所在公里格网点作为控制点，采用区域面积加权的方法进行加权求和转换。而所谓区域面积加权，指的是以数据点与所在公里格网构成的区域面积为权重，分别对控制点改正值进行加权。该方法能够使得位于格网线上的数据点收敛于格网线上两点，位格网点上的数据点收敛于该格网点，因此，不会在格网边界上出现转换不一致的情况。逐格网纠正的具体方法如下。

图2　基于公里网约束的空间数据坐标变换示意图

如图2(b)所示，数据点P位于格网P1P2P3P4中，过P点作水平线和垂直线分别与格网线相交，构成区域分别为S1、S2、S3、S4。设4个格网点P1、P2、P3、P4的变换改正值为(Dx1，Dy1)、(Dx2，Dy2)、(Dx3，Dy3)、(Dx4，Dy4)，每个格网点对应的权重为该格网点的对角点所构成的面积，如P1的权重为S3、P3的权重为S1，则P点的坐标改正值(Dx，Dy)为

(1)

式中，S=S1+S2+S3+S4，0≤Si≤S，i=1,2,3,4。

当点P位于格网线上时，P点的变换值将收敛于格网线上两点，其值只与该点在格网线的位置相关。这样，不管P点是在该格网内求解，还是在相邻格网内求解，其变换值是相同的，不会出现变换结果不一致的情况。如图2(c)所示，P点位于格网线P2P3上，显然S2=S3=0，因此，P点的变换值就收敛于P2、P3，其权重比值可简化为线段PP3与线段PP2的长度之比。

当点P位于格网点上时，P点的变换值将收敛于该格网点，其值与该点的改正值相同，显然，在相邻格网中对该点变换值的求解结果也是一致的。图2(d)所示，P点与P2重合，显然S1=S2=S3=0，因此，P点的变换值就等于P2的改正值。

鉴于我国保密的要求，控制点的解算往往有一定误差，这个误差会给变换数据点带来一定的影响。显然，该变换属于线性变换，根据线性函数的误差传播公式，有

(2)

式中，mz为变换点的误差；m1、m2、m3、m4分别为格网4点的误差；k1、k2、k3、k4分别为格网4点的权重，且k1+k2+k3+k4=1。

因此，可得

(3)

式(3)表明，如果公里格网点的坐标改正量存在误差，其传播给内部转换点的误差不会大于各网点误差的最大值，因此，从误差传递角度看，控制点的误差不会对变换构成影响。

从算法效率来看，算法的基本步骤就是上述计算公式，其值可直接计算，因此算法效率为数据规模n的线性阶O(n)。

二、逐公里格网平面坐标转换实现过程

1. 公里格网的布设

国家标准图按国家测绘规范对整个高斯-克吕格带布设1 km×1 km的公里格网，每个格网点记录当前坐标值和待转换目标坐标值。这样，格网点的变换改正值就为待转换目标坐标值与当前坐标值之差。

2. 坐标转换计算

读取待转换数据坐标点，单位为m，先按照格网索引快速定位到所在格网，然后计算格网控制点的权重S1、S2、S3、S4，最后利用式(1)得到坐标变换值。当数据点在高斯-克吕格条带边上，所用到的公里格网控制点则需要通过相邻高斯-克吕格投影带的控制点计算。具体计算步骤如下：

2) 权重的计算。确定数据点所在格网的行列号(i,j)之后，该格网的x方向最大最小值分别为1000j和1000(j-1)，y方向最大最小值分别为1000i和1000(i-1)，再加上数据点坐标值(x,y)，可得4个格网控制点所对应的权重值(如图3所示)。

3) 将步骤2)得到的权重值代入式(1)，得到数据点的变换值(Dx,Dy)，之后将坐标变换值与原坐标值求和为变换后的坐标值，即为(Dx+x,Dy+y)。

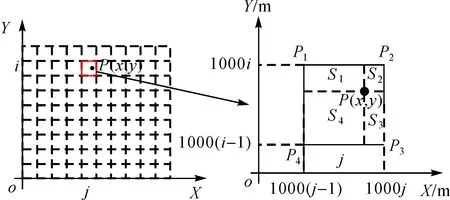
图3　坐标转换权重计算示意图

3. 试验与转换精度分析

试验数据采用安徽省滁州市沙河镇、施集镇、大柳乡、乌衣镇4个样区1∶1万数据(点数分别为188、248、134、162个)，以及其对应的格网控制点数据，坐标系统分别为1954北京坐标系和CGCS2000，投影系统为高斯-克吕格投影。采用本模型将4个样区1954北京坐标系数据转换成CGCS2000，再将转换后的数据与原始CGCS2000数据进行精度分析，统计中误差和最大误差，结果见表1。

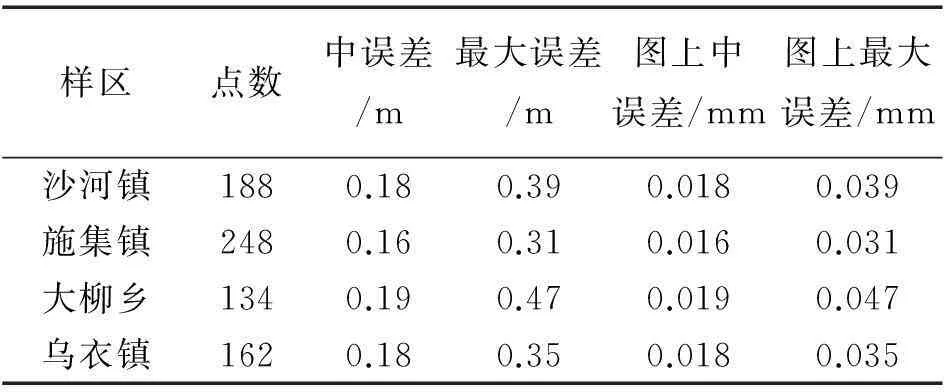
表1　坐标转换精度分析结果表

从试验结果来看，4个样区坐标转换的转换精度不管是中误差还是最大误差，都完全满足地图精度要求(不大于0.1 mm)。

三、结束语

本文建立的基于公里格网约束的大区域平面坐标快速转换模型，通过原理分析与试验验证，具有以下优点：一是该模型是通过公里格网约束进行大区域数据的坐标转换，其处理过程不受图幅边界的影响，不需分幅或分区转换；二是在精度、效率及转换结果的唯一性等方面，均能较好满足大区域坐标转换的需求；三是该模型无须提供高度保密的控制点坐标信息，只需提供公里格网坐标信息(其可通过解算公布)，避免了保密和公共服务的矛盾。因此，该模型是一个具有良好普适性的通用转换系统，具有较好的推广价值。

参考文献：

[1]魏子卿.我国大地坐标系的换代问题[J].武汉大学学报(信息科学版)，2003，8(2)：138-144．

[2]陈俊勇.中国现代大地基准——中国大地坐标系统2000(CGCS 2000)及其框架测[J].测绘学报，2008，37(3)：269-271．

[3]王解先.七参数转换中参数之间的相关性[J].大地测量与地球动力学，2007，27(2)：43-46．

[4]李德仁，朱欣焰，龚健雅.从数字地图到空间信息网格——空间信息多级网格理论思考[J].武汉大学学报(信息科学版)，2003，28(6)：642-650．

[5]张顺卿.1980年国家大地坐标系与地形图数学基础的变换[J].地图，1993(1)：32-36．

[6]闫正，杜道生，夏林元.城市地理信息系统标准化指南[M].北京：科学出版社，1998．

[7]吕志平，张建军，乔书波.大地测量学基础[M].北京：解放军出版社，2005.

[8]韩雪培，廖帮固.海岸带数据集成中的空间坐标转换研究[J].武汉大学学报(信息科学版)， 2004，29(10)：933-936．

[9]王解先，王军，陆彩萍.WGS-84与北京54坐标的转换问题[J].大地测量与地球动力学，2003， 23(3)：70-73．

[10]欧朝敏，黄梦龙.地方坐标到2000国家大地坐标转换方法研究[J].测绘通报，2010(9)：26-28．

[11]谢鸣宇，姚宜斌.三维空间与二维空间七参数转换参数求解新方法[J].大地测量与地球动力学，2008，28(2)：104-109．