一种基于线性KD树的点云数据组织方法

陈茂霖，万幼川，田思忆，秦家鑫，卢维欣

(1. 武汉大学遥感信息工程学院，湖北 武汉 430079； 2. 武汉市测绘研究院，湖北 武汉 430022)

A Method of Organizing Point Clouds Based on Linear KD Tree

CHEN Maolin，WAN Youchuan，TIAN Siyi，QIN Jiaxin，LU Weixin



一种基于线性KD树的点云数据组织方法

陈茂霖1，万幼川1，田思忆2，秦家鑫1，卢维欣1

(1. 武汉大学遥感信息工程学院，湖北 武汉 430079； 2. 武汉市测绘研究院，湖北 武汉 430022)

A Method of Organizing Point Clouds Based on Linear KD Tree

CHEN Maolin，WAN Youchuan，TIAN Siyi，QIN Jiaxin，LU Weixin

摘要：常规KD树索引对大规模点云数据进行组织和管理时，指针的存储往往耗费大量的内存空间。本文结合线性索引的编码思想，提出了一种线性KD树索引的构建和查找方法，存储点云时可以充分利用内存空间，通过自然数编码表示结点间的关系，并给出了线性KD树的构建和邻域查找方法。最后通过与开源最临近搜索库ANN库进行对比试验，证明本文的线性KD树索引可以明显减少点云组织时的内存消耗，并与基于指针的ANN库具有相近的临近查找效率。

关键词：点云索引；点云组织；邻域查找；KD树；线性索引

随着激光扫描技术的发展，大规模的点云数据不断产生，点云数据的组织和管理已经成为后续处理和应用中的瓶颈[1]。点云数据的后处理往往依赖于点云的索引技术[2]，一个高效的点云索引不仅可以提高点云的处理效率，还可以节省计算机的存储空间。

KD树索引是点云数据处理中常用的一种索引方式，由Bentley在1975年提出[3]，是二叉查找树在多维空间的扩展，在点云数据处理中具有广泛的应用。在KD树被提出后，有大量的论文对KD树索引的理论和应用进行了研究和改进。Nene提出了KD树在高维搜索中高效应用的方法[4]；Greenspan通过改进KD树索引来提高ICP算法的效率[5]；Horn等通过GPU对KD树索引进行加速[6]；此外KD树还被应用在点云简化[7]、去噪[8]等不同的应用中。在多数研究中，其关注点主要集中在检索效率、索引维度、索引应用等方面，KD树结点间的关系主要通过指针记录，在上千万甚至上亿的点云数据量中，传统KD树索引中的指针维护往往要占据大量的内存，造成内存空间的浪费甚至无法构树等问题。

本文将线性索引的编码思想与KD树索引结合，提出了一种线性KD树索引的构建方法。该方通过编码的方式表示KD树结点间的关系，避免了指针的使用，解决了传统KD树在存储点云时需要维护大量指针而造成的内存浪费问题。同时，索引中的结点关系可以通过文件方式存储，点云构建索引并存储为文件后，可以按照索引顺序从文件中读入而无须再次构树，进而提高了点云读入和处理的效率。

一、线性KD树索引的构建

在数字图像处理和地理信息系统等领域，人们一般采用线性四叉树取代常规四叉树方法[9]，通过一定的编码方式对数据进行划分，比普通四叉树大大节省了存储空间,且蕴含有层次特性[10]。受线性索引思想的启发，本文将线性索引编码的方式应用于KD树结点关系构建过程中，使用自然数编码的方式表示KD树中相邻结点间的关系，从而减少了索引的内存空间占用。

1. 线性KD树的编码规则

本文提出的线性KD树将根节点Pr的编码I(P)标记为1，同时放在结点序列的第1个位置，Pr的两个子结点的编码分别为2和3，分别放在结点序列的第2和第3个位置。对于一个数量为M的节点序列，线性KD树的编码规则如下：

1) 根结点Pr的编码为1。

2) 对于KD树中不为根结点的任意结点Pi，令其编码为I(Pi)，则其两个子结点的编码分别为2×I(Pi)和2×I(Pi)+1，其父节点的编码为[(I(Pi)/2),]为向下取整，结点Pi在结点序列的第I(Pi)个位置。若2×I(Pi)>M，则该结点没有子结点，为叶子结点。

图1所示为常规KD树与线性KD树结点关系的对比。常规KD树利用大量指针来表示结点之间的关系，存储空间的利用率低；而线性KD树通过结点在序列中的位置编码，描述了结点之间的关系，节省了大量的内存空间。同时，由于编码与结点在内存序列中的位置相对应，每个结点中不需要存储其对应的编码值，进一步提高了存储空间的利用效率。

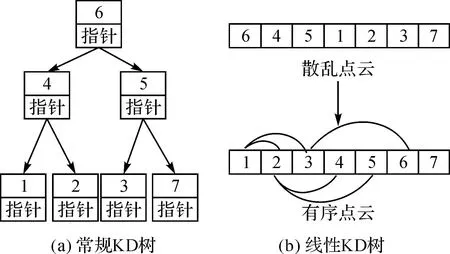
图1　常规KD树与线性KD树的组织方式对比

2. 线性KD树的构建方法

本文提出的线性KD树不仅可以通过散乱的点云序列进行构建，对于按照编码顺序存储的点云文件，还可以在顺序读取点云时直接从文件中生成KD树索引，提高了点云数据的组织和管理效率。

(1) 散乱点云序列的构树方法

面向散乱点云序列的线性KD树构建方法基于快速排序算法中的划分交换思想[11]，通过不断交换和迭代来寻找每层的根结点，最终构建出完整的KD树。

令Q(1，M)表示大小为M的无序点云序列，Q(i,j)表示整体点云序列中从i到j的一段子序列，q[i][k]表示整体点云序列中第i个结点的第k个坐标值，k取值为0、1和2时分别对应x、y和z坐标，QI(i,j)则表示平衡后的有序多点云序列。具体构建方法如下：

1) 空间分辨器的选择。在KD树的每一层，选择对应空间中最长的坐标轴对应的坐标作为KD树在该层的分辨器(discriminator)。这样可以最大限度上保证空间的均衡划分。

2) 划分交换。在KD树当前层次对应的结点序列Q(i,j)中，取中间点作为当前层次的根结点，令其序号为median，并根据其父节点的编码计算当前结点的编码index。令d为当前最长数据轴所对应的分辨器，取i和j分别为start和end。执行划分交换算法：

PointPartition(start, end)

while(start

if(q[start][d]q[median][d])

swap(q[start], q[end]) ∥交换结点

end if

start++

end--

end while

在划分交换算法执行完毕后，令QI[index]=Q[median]，记录当前层次下的根结点，并可以对划分后的两个区间继续执行划分交换。

3) 递归构树。在每一层的划分交换算法基础上，通过递归的方法，为KD树的每一层寻找对应结点，计算编码值，并为下一层的划分交换算法提供所属点云序列，最终构成一个完整的KD树，如图2所示。具体算法如下：

PointSort (start, end, index)

median=PointPartition (start, end)

QI[index]=Q[median]

if(start

start=start

end=median-1

index=2*index

PointSort (start, end, index) ∥递归调用

end if

if(end>median)

start=median+1

end=end

index=2*index+1

PointSort (start, end, index) ∥递归调用

end if

图2　线性KD树的编码和构建过程

在迭代算法结束之后，QI(1，M)便构成了线性KD树的结点序列，通过一个结点的编码可以在序列中快速查找其对应的父节点和子结点。

(2) 基于点云文件的构树方法

由于线性KD树每个结点的编码与其在内存序列中的位置保持一致，因此线性KD树中的结点按照编码顺序保存为点云文件后，按照存储顺序再次读入时无须执行构树算法便可以直接构建索引，明显增加了点云的组织和管理效率，其存储格式见表1。

表1　线性KD树的文件存储格式

综合以上两种方法，本文提出的线性KD树索引可以基于无序点云序列及编码后的点云文件两种方式灵活构建，如图3所示，提高了点云数据的组织和管理效率。

图3　线性KD树的构建方式

3. 线性KD树的邻域搜索

多维空间中的临近搜索一般根据搜索半径ε将查找范围限制在一个由多维面构成的空间中。如三维空间的查找是限制在一个边长为2ε的正方体中，然后寻找距离中心点小于ε的点，如图4所示。

图4　三维空间中的临近查找

本文中的线性KD树也基于这种思想进行邻域查找，令r为邻域半径，进行搜索的中心点为PCenter，则邻域搜索方法如下：

1) 确定搜索起点的结点编码index，一般取index为1。

2) 若当前待搜索结点QI[index]为叶子结点，进入步骤4)；若QI[index]不为叶子结点，则进入步骤3)。

3) 计算QI[index]对应的分辨器d，进而计算PCenter到当前分割平面的距离dist。若dist大于搜索半径r，表明分割平面两侧的空间中都可能存在邻域中的点，取当前待搜索的结点编码分别为2×index和2×index+1，分别执行步骤2)；若dist小于搜索半径r，表明邻域中的点只存在于分割平面的一侧，通过比较PCenter[d]与QI[index][d] 确定待搜索结点的编码，PCenter[d]小于QI[index][d]时，待搜索结点的编码取为2×index，否则取为2×index+1，执行步骤2)。

4) 若QI[index]与中心点PCenter的距离小于r，将当前搜索结点QI[index]加入邻域集合，并将集合按照与中心点PCenter的距离从小到大进行排序。在没有可搜索结点后，结束整个邻域搜索算法。

从整体上看，线性KD树中的邻域查找利用上下层结点编码间的关系进行递归查找，其查找顺序与结点编码保持一致，由于将查找范围限制在一个边长为2r的正方体空间内，因此实际遍历结点远少于KD树中的结点数目。图5所示为一个线性KD树的遍历查找过程，黑色结点为中心点，1、3、6、13的深灰色结点为落在邻域中的结点，2和7为遍历但没有落在邻域中的结点，白色结点是落在正方体空间之外而未遍历的结点，实际遍历结点只占总结点数目的一半，大大提高了邻域搜索的效率。

图5　线性KD树临近查找的过程

二、试验与分析

为了验证线性KD树(linear KD-Tree,LKD)在点云管理、查找等方面的性能，本文将线性KD树索引同最临近搜索开源库ANN库[12](approximate nearestn neighbor searching)在不同的三维点云数据中进行了对比试验。试验数据如图6所示，其中图6(a)为机载点云数据，包含1 424 805个点;图6(b)为新疆某地野外的地面激光点云数据，包含6 079 124个点；图6(c)为天津民园雕塑点云数据，包含9 092 351个点;图6(d)为武汉东湖石刻点云数据，包含16 354 184个点。试验使用的计算机配置为Core(TM) i5-4460处理器，8 GB内存。

图6　点云试验数据

表2为两种索引在不同试验数据下的构建效率与内存占用情况的试验结果。试验结果表明，由于避免了指针的使用，线性KD树对内存的消耗仅为ANN库的1/3，显著降低了点云存储对计算机内存的占用。同时，由于在构树过程中，ANN库需要动态开辟大量超出实际存储量的临时内存，在对数据量为1600万的点云进行构树时，产生了内存不足的问题而导致构建失败；而线性KD树的构建过程主要在点云序列内部进行划分交换，对于计算机内存的利用更加合理，可以处理数据量更大的点云数据。此外，从索引构建的试验结果来看，本文提出的线性KD树索引构建效率约为ANN库的2.5倍，且对于上千万的点云可以在10 s之内完成构建，具有较好的索引构建效率。

表2　线性KD树与ANN库的对比

为了测试线性KD树的邻域查找效率，使用线性KD树和ANN库对图6(c)中的点云数据进行试验，分别计算两种索引在不同邻域半径下对点云中所有点进行邻域近查找所需的总时间和每个点进行邻域查找所需的平均时间，试验结果如图7所示。其中，试验点云数据的密度为4~6 mm，图7(a)为不同半径下对所有点执行一遍最临近查找所需要的总时间；图7(b)为不同半径下对每个点进行查找所需的平均时间，所有的数据均使用5次相同操作的平均数据。从试验结果可知，本文提出的线性KD树索引在三维空间中的邻域查找效率与基于指针的ANN库十分接近，在千万级的点云数据中，每个点所需的平均查找时间保持在10-5s的数量级上，可以实现高效的点云邻域查找。

图7　邻域查找时间对比

三、结束语

随着生产中获取的点云数据规模不断增大，如何合理利用计算机内存对点云进行组织成为一个不容忽视的问题。本文通过引入线性索引的编码思想改进传统基于指针的KD树索引，提出了线性KD树索引的构建和邻域查找方法；通过试验证明线性KD树索引的内存占用约为基于指针的开源ANN库的1/3，并且具有与ANN库几乎相同的查找效率，对于点云数据的组织和空间查找提供了高效的索引基础。本文主要针对三维空间中的点云进行了KD树索引构建和查找方法的设计，对于高维度数据中的索引高效构建和查找方法还有待进一步的研究。

参考文献：

[1]杨建思. 一种四叉树与KD树结合的海量机载LiDAR数据组织管理方法[J].武汉大学学报(信息科学版)， 2014，39(8)：918-922.

[2]赖祖龙, 万幼川,申邵洪,等.基于Hilbert排列码与R树的海量LIDAR点云索引[J].测绘科学, 2009, 34(6): 128-130.

[3]BENTLEY J L. Multidimensional Binary Search Trees Used for Associative Searching[J]. Communications of the ACM, 1975, 18(9): 509-517.

[4]NENE S A, NAYAR S K. A Simple Algorithm for Nearest Neighbor Search in High Dimensions[J]. IEEE Pattern Analysis and Machine Intelligence, 1997, 19(9): 989-1003.

[5]GREENSPAN M, YURICK M. Approximate KD Tree Search for Efficient ICP[C]∥Proceedings of Fourth International Conference on 3-D Digital Imaging and Modeling. [S.l.]: IEEE, 2003: 442-448.

[6]HORN D R, SUGERMAN J, HOUSTON M, et al. Interactive KD Tree GPU Raytracing[C]∥Proceedings of the 2007 Symposium on Interactive 3D Graphics and Games.[S.l.]: ACM, 2007: 167-174.

[7]蔡志敏, 王晏民, 黄明.基于KD树散乱点云数据的Guass平均曲率精简算法[J]. 测绘通报, 2013(S1): 44-46.

[8]张毅, 刘旭敏, 隋颖, 等.基于K-近邻点云去噪算法的研究与改进[J].计算机应用, 2009, 29(4): 1011-1014.

[9]龚健雅.一种基于自然数的线性四叉树编码[J].测绘学报, 1992, 21(2): 90-99.

[10]肖乐斌, 龚建华, 谢传节. 线性四叉树和线性八叉树邻域寻找的一种新算法[J].测绘学报,1998,27(3):195-203.

[11]HOARE C A R.Quicksort[J]. The Computer Journal, 1962, 5(1): 10-16.

[12]ARYA S, MOUNT D M, NETANYAHU N S, et al. An Optimal Algorithm for Approximate Nearest Neighbor Searching Fixed Dimensions[J].Journal of the ACM (JACM), 1998, 45(6): 891-923.

引文格式： 陈茂霖，万幼川，田思忆，等. 一种基于线性KD树的点云数据组织方法[J].测绘通报，2016(1)：23-27.DOI:10.13474/j.cnki.11-2246.2016.0006.

作者简介：陈茂霖(1991—)，男，博士生，主要研究方向为地面激光数据处理。E-mail:maolinchen@qq.com

基金项目：国家863计划(2013AA122104)；高等学校博士学科点专项科研基金(20130141130003)

收稿日期：2014-11-17

中图分类号：P237

文献标识码：B

文章编号：0494-0911(2016)01-0023-05