具有间隙非线性的全动舵系统的颤振分析

张恩阳，宋荣志，冯琨程，陆振玉

(中国科学院 长春光学精密机械与物理研究所，长春　130033)



具有间隙非线性的全动舵系统的颤振分析

张恩阳，宋荣志，冯琨程，陆振玉

(中国科学院 长春光学精密机械与物理研究所，长春130033)

摘要：研究了超声速来流中含间隙舵系统的颤振问题。通过建立舵机传动机构的动力学方程并采用翼段模型和活塞理论，导出了俯仰方向含有间隙的舵面的非线性气动弹性动力学方程，利用Hopf分叉理论计算了舵面的颤振速度，并采用描述函数法分析了含间隙舵面的气动弹性响应。在此基础上，研究了传动机构的动态特性和间隙对舵面的颤振速度和极限环振荡行为的影响。研究表明：舵机静刚度较低时，需要考虑其动刚度对颤振速度的影响；仅当间隙内的俯仰刚度较小时，舵面的气弹响应才会发生亚临界Hopf分叉；在飞行速度一定的情况下，间隙量增大1倍，极限环振荡的振幅近似增加1倍。

关键词：间隙非线性；动刚度；颤振；极限环振荡；Hopf分叉；描述函数法

本文引用格式：张恩阳，宋荣志，冯琨程，等.具有间隙非线性的全动舵系统的颤振分析[J].兵器装备工程学报，2016(1):136-141.

Citation format:ZHANG En-yang, SONG Rong-zhi, FENG Kun-cheng,et al.Flutter Analysis of System of All Movable Fin with Freeplay Nonlinearity [J].Journal of Ordnance Equipment Engineering,2016(1):136-141.

颤振是当结构在流体中的相对运动速度超过临界速度时，结构因受到气动力、惯性力和弹性力的相互作用而产生的气动弹性失稳现象[1]。这种不稳定现象可能会导致飞行器结构发生破坏或者引起飞行器操控性能的下降。所以，准确地预测飞行器的气动弹性性能以防止发生气动弹性不稳定非常重要。目前工程界对飞行器的大多数气动弹性分析都是在结构线性的假设下进行的，实际工程应用中往往存在结构非线性环节。结构非线性可以分为分布非线性和集中非线性。集中非线性作用在局部位置，例如控制表面铰链处存在非线性。分布非线性在整个结构中都存在，例如材料非线性，几何非线性和屈曲。集中非线性包括3次刚度非线性，间隙，摩擦和迟滞等，控制表面铰链的磨损或加工公差会引起这种非线性。这些非线性环节会导致气动弹性系统在一定条件下出现极限环振荡和混沌现象，这些现象比线性系统的响应复杂得多[2]。

针对不同类型的结构非线性所引起的气动弹性不稳定问题，学者们做过大量的理论和数值研究[3-8]。由于间隙非线性在工程实践中普遍存在，其研究难度也较大，所以引起了人们的广泛关注[7-12]。Laurenson和Trn[9]分析了含间隙的二维模型，他们采用描述函数法，发现在线性颤振边界之内会发生极限环振荡。赵永辉等[10]分析了亚声速不可压缩流作用下具有操纵面间隙非线性翼段结构的气动弹性响应，指出铰链间隙的存在使机翼发生极限环振荡和跳跃。任爱娣等[11]对具有不对称间隙的二元机翼的自激振动在小于线性颤振速度时可能出现的多种周期运动进行了研究。贾尚帅等[12]研究了含间隙超音速二元弹翼的非线性颤振与主动控制问题，他们利用Hopf分叉理论、描述函数法和数值方法分析了系统的非线性颤振特性。

前述这些研究都是针对含间隙的固定翼面进行气动弹性分析。对于含间隙的舵系统来说，舵机传动机构的动态特性会影响气动弹性响应，例如影响线性颤振速度和极限环振荡的振幅。Shin等[13]利用迭代V-g法分析了驱动器的非线性对驱动器的动力学特性和亚声速舵面的气弹特性的影响。杨宁等[14]利用迭代V-g法和时域仿真方法研究了结构非线性、舵机动刚度和控制指令对亚声速舵面的极限环振荡的影响。目前，同时考虑间隙非线性和舵机动刚度对舵系统的气动弹性特性影响的学术研究非常有限。因此，本研究基于翼段模型和超声速活塞理论，利用Hopf分叉理论和描述函数法对这一问题进行了理论研究。通过理论分析，给出了颤振速度的方程式，从而可以直接得出颤振速度与舵机传动机构参数的关系以及速度与极限环振荡振幅的关系。在此基础上深入讨论了间隙非线性对气动弹性特性的影响，研究结果可为工程研究提供理论参考。

1建模和分析

如图1所示，本研究考虑的舵系统由传动机构和舵面两部分构成，其中传动机构由伺服电机和齿轮减速器组成。舵系统工作时，伺服电机根据控制指令，带动齿轮减速器转动，在舵轴上提供输出力矩，带动舵面作俯仰运动。当需要将舵面保持在某一俯仰角时，伺服电机无指令输入，电机输出轴锁死。本文仅考虑电机输出轴锁死情况下，舵系统的气动弹性稳定性问题。下面将分别对传动机构和舵面建立传动机构动力学模型和二维翼段动力学模型，然后将这两者组合起来导出整个舵系统的动力学模型，进而利用Hopf分叉理论对舵系统进行颤振分析，并采用描述函数法来分析间隙非线性对极限环振荡的影响。

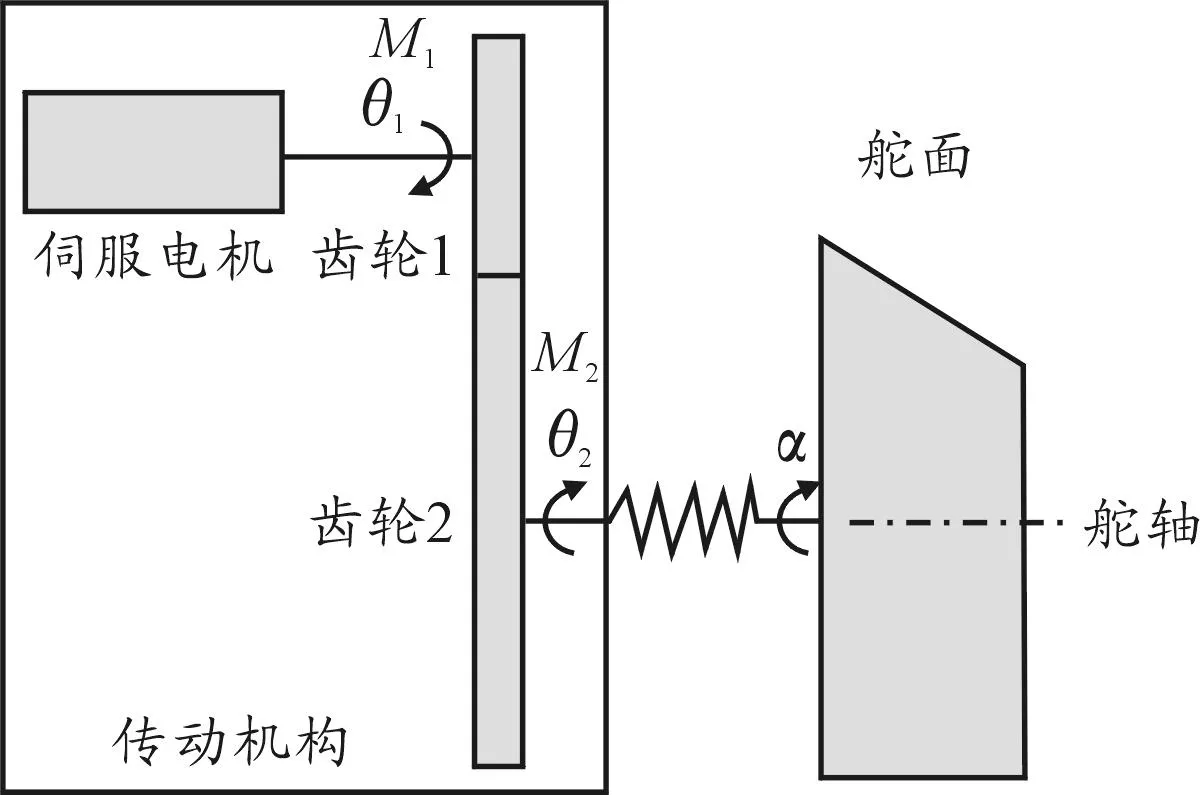
图1　舵系统构成

1.1建模

1.1.1传动机构模型

电机轴锁死，电机的抗扭力矩M1与齿轮1的转角θ1有如下关系:

(1)其中ka和ca分别为传动机构在输入端(电机输出轴)的等效刚度和等效阻尼。

齿轮1的动力学方程为

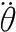
齿轮2的动力学方程为

(3)其中：r2为齿轮2的半径；J2为齿轮2的转动惯量；M2为舵轴上的力矩；θ2为齿轮2的转角，且r2=nr1，θ2=θ1/n。

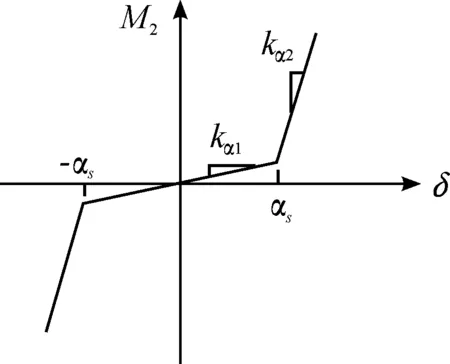
图2　间隙非线性函数

(4)其中α为舵面的俯仰角。当不存在非线性刚度或者间隙时，M2=kl(α-θ2)，kl为线性刚度。计δ=α-θ2，由于摩擦的存在，当δ在间隙角范围之内，舵轴也具有一定的刚度[15-16]。为简化问题，可用双线性弹簧模型来模拟考虑间隙非线性，其表达式为

(5)其中：αs为间隙角；kα1为间隙角度内的线性刚度；kα2为间隙角度外的线性刚度。它所表示的力矩-角度曲线如图2所示。

由上述方程可得

(6)

1.1.2翼段模型

舵面被简化为具有浮沉和俯仰两个自由度的二维翼段。根据拉格朗日方程，可得到翼段的运动方程

(7)

(8)其中：h为弹性轴的沉浮位移，向下为正；α为翼段的俯仰角，抬头为正；m,mbxα和Iα为单位展长舵面的质量，对弹性轴的质量静矩和对弹性轴的质量转动惯量；ch和cα分别为沉浮和俯仰阻尼系数；kh为沉浮刚度；f(α-θ2)表示间隙非线性。L和M为气动升力和绕弹性轴的气动力矩，b为半弦长,bxα为重心G到弹性轴E的距离，bε为气动中心A到弹性轴E的距离。升力和气动力矩的表达式为

(9)

(10)其中：Δp为下表面与上表面的压差；MA为绕气动中心的气动力矩。

图3　翼段模型

(11)其中：ρ∞为大气密度；a∞为声速；vl和vl分别为舵面下表面和上表面的法向速度；z为舵面上表面的法向位移；V为来流速度。对于二维翼段，z=-h-xα，故有

(12)将方程式代入方程式(9)和方程式(10)，可得:

(13)

(14)将升力和气动力矩表达式代入翼段动力学方程式和方程式可得:

(15)

(16)

1.1.3系统动力学方程

将传动机构动力学方程与翼段动力学方程联立，可得系统动力学方程:

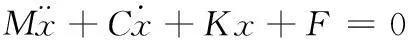
(17)其中M,C和K分别为质量矩阵，阻尼矩阵和刚度矩阵，F为力列阵。

进行广义坐标变换

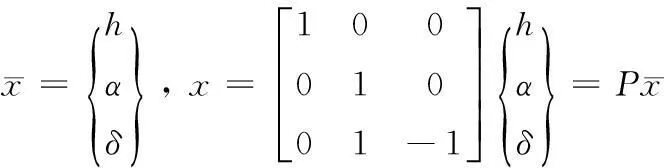
可得

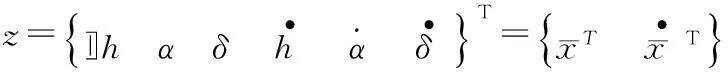
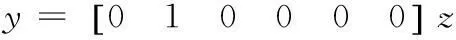
(20)其中y为输出。

1.2分析

1.2.1基于Hopf分叉理论的颤振分析

对于本文所考虑的含间隙非线性的舵系统，状态方程为分段线性方程:

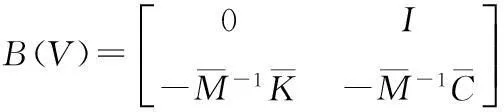
根据动力系统的Hopf分叉理论[17]可知，当B(V)的特征值从实部为负数的复数变为纯虚数，系统在平衡点z=0发生Hopf分叉。B(V)的特征值方程为

(24)对于无传动机构的情况，仅根据翼段动力学方程即可得出其特征方程为

(25)展开可得:

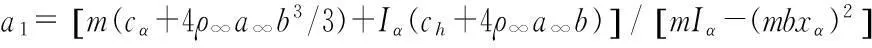
设λ=jβ，则β4-ja1β3-a2β2+ja3β+a4=0。

分离其实部和虚部，可得

所以颤振速度方程

(27)颤振频率为

(28)有传动机构的情况下，特征方程为：

展开可得

(30)

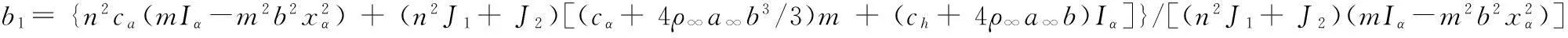
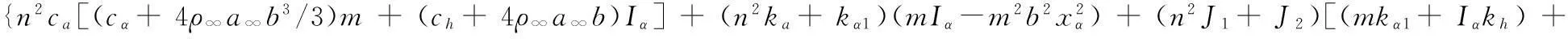
b3= {n2ca[(mkα1+Iαkh) + (ch+ 4ρ∞a∞b)(cα+ 4ρ∞a∞b3/3)-4ρ∞a∞Vbmbxα]+ (n2J1+J2)[(ch+ 4ρ∞a∞b)kα1+

b4= {n2ca[(ch+ 4ρ∞a∞b)kα1+ (cα+ 4ρ∞a∞b3/3)kh] + (n2J1+J2)khkα1+ (n2ka+kα1)[(mkα1+Iαkh) +

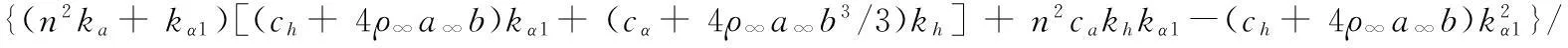
设λ=jβ，则

分离其实部和虚部可得

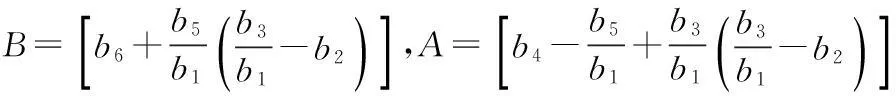
所以颤振速度方程为

(31)

解此方程，其实根即为颤振速度Vf。将Vf代入B和A，可算出颤振频率

(32)

1.2.2基于描述函数法的间隙非线性分析方法

描述函数法是对正弦信号在非线性特性作用下的输出进行谐波线性化处理所得到的近似描述。它被广泛用于获得非线性气动弹性系统的等效线性系统[18]。在通常情况下，利用这种等效线性化方法获得的极限环振荡特性与用数值仿真获得的结果一致性很好[12,15]。因此，本文采用描述函数法来计算在一定振幅下，双线性力矩-角度函数的等效线性刚度。函数对应的等效刚度的表达式为

(33)

其中φ=arcsin(αs/A)。

所以对于一定的振幅A，用方程式计算等效线性刚度ke，然后用ke代替方程式和方程式中的kα1，即可得到振幅A对应的速度和频率。

2结果与讨论

取系统模型参数为：m=20 kg,χα=0.25,b=0.5 m,ε=0.15,Iα=1.25 kg·m2,ch=172 kg/s,cα=337.5 kg·m2/s,kh=147 920 N/m,kα1=2 000 N·m/rad,kα2=91 125 N·m/rad,J1=0.05 kg·m2,J2=5 kg·m2,n=10,ka=10 000 N·m/rad,ca=3.16,αs=π/180。利用在上一节导出的理论公式，可得出舵系统的颤振速度和极限环振荡响应，进而可分析传动机构的动刚度和间隙非线性对系统气动弹性特性的影响。

2.1传动机构动态刚度的影响

图4给出了舵机传动机构的静刚度和动刚度对颤振速度的影响。其中，静刚度情况是指仅考虑传动机构在舵轴的等效静刚度(n2kα)，所以实际俯仰刚度为n2kakα2/(n2ka+kα2)。可根据方程式得到图4所示的颤振速度曲线(实线)。动刚度情况则考虑传动机构的刚度、惯性和阻尼的影响，需要根据方程式计算得到颤振速度曲线(虚线)。由图4可知，当传动机构刚度较大(>105N·m/rad)时，它对颤振速度的影响较小；当传动机构刚度较小时，颤振速度随着刚度的降低而迅速减小；而且根据静刚度计算的舵面颤振速度偏高，因而这种计算方法是不安全的。所以在分析计算舵面的颤振速度和气弹响应时，必须考虑舵机传动机构的动刚度。

2.2间隙非线性的影响

图5给出了等效线性刚度与振幅的关系。当振幅小于间隙αs时，ke=kα1；当振幅大于间隙αs时，等效线性刚度随着振幅的增大而增大。且当振幅远大于间隙αs时，ke趋近于kα2。

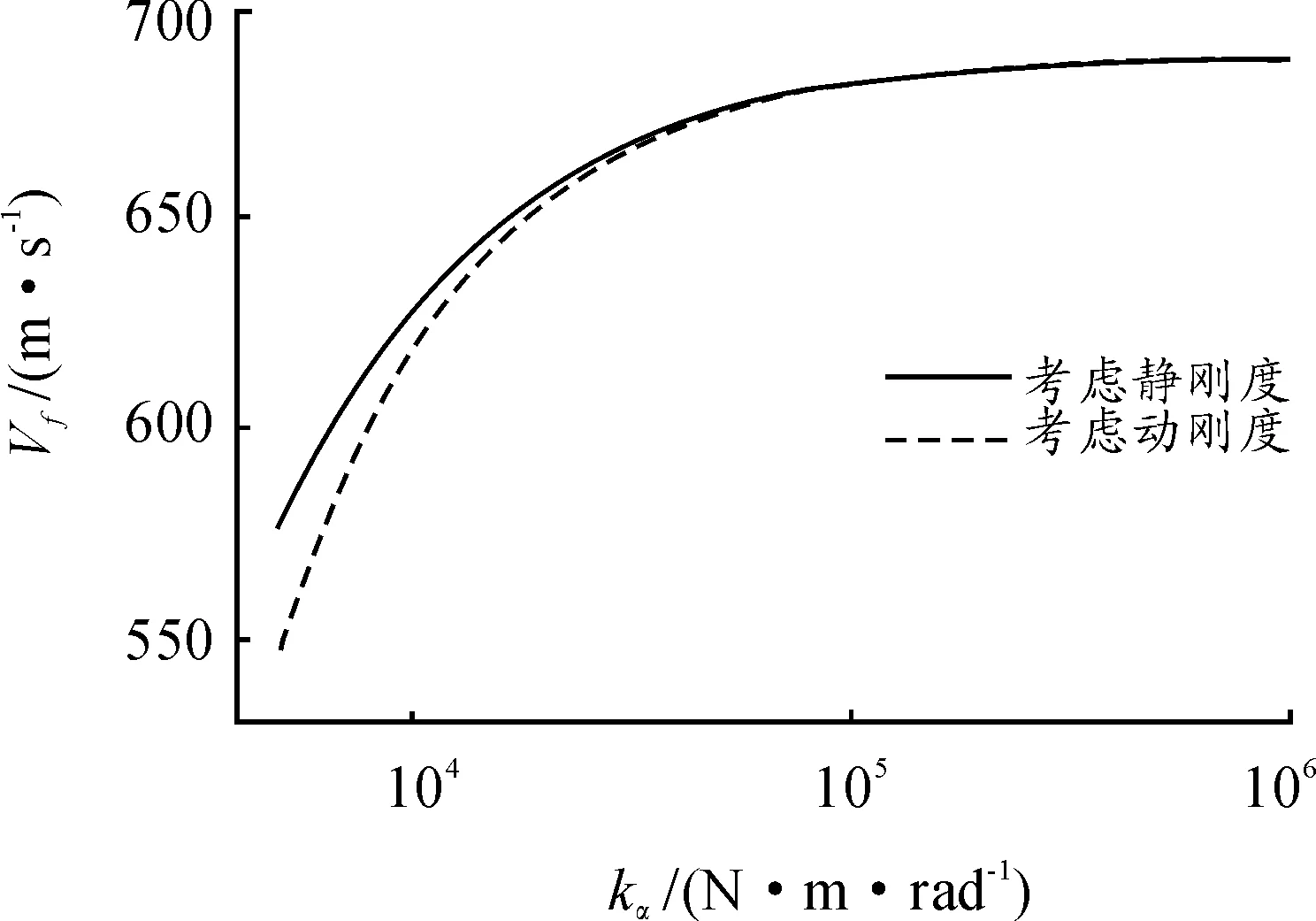
图4　传动机构刚度对颤振速度的影响

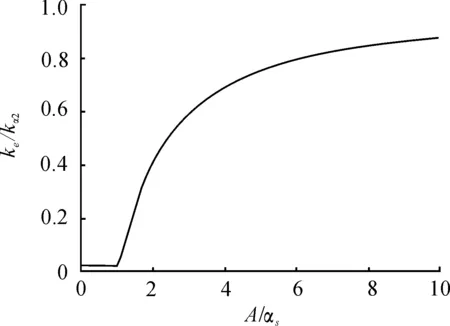
图5　等效线性刚度随振幅的变化

当振幅限制在间隙范围之内时，舵面当速度达到临界颤振速度Vf时发生等幅振荡(图6中点划线)。当速度超过临界颤振速度，舵面的振幅被限制在一定范围之内(图6中实线)。这是因为，当实际振幅超过图中实线所限定的值时，舵面的等效刚度增加；刚度越大，发生颤振(维持等幅振荡)所需的颤振临界速度越高；而实际速度维持不变，所以振幅必然会衰减，直至衰减到所限定的值。而当速度从较高的值(>Vf)降至略低于Vf，舵面仍然会发生极限环振荡(图6中实线)。发生极限环振动的临界速度为亚临界分叉速度。另外，如图7所示，极限环振荡的频率随着振幅的增大而增大。

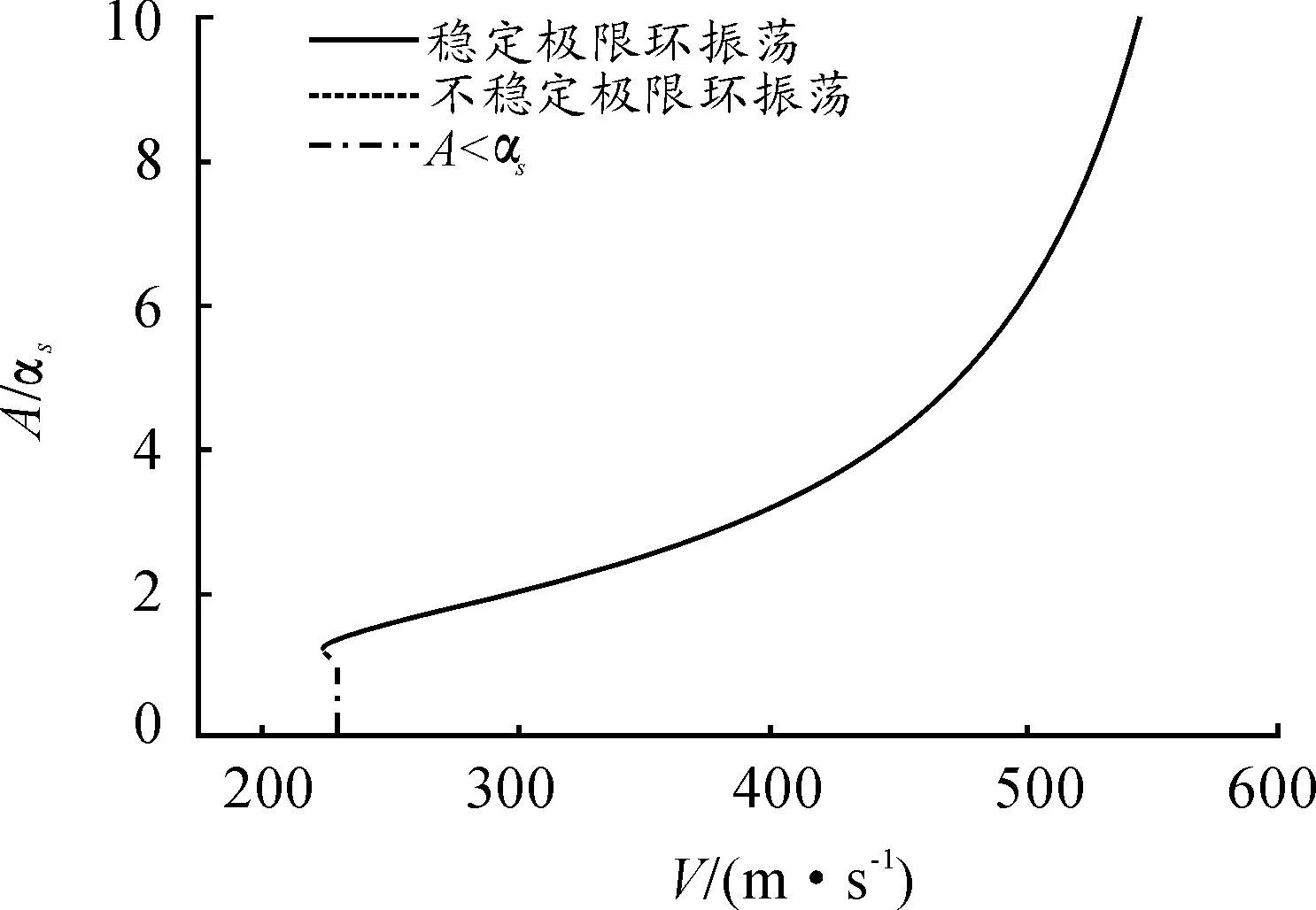
图6　极限环振荡的振幅随速度的变化

图8比较了不同间隙量情况下极限环振荡的振幅与速度的关系。在kα1一定时，颤振临界速度与间隙量无关。但是间隙越小，维持一定幅度振荡所需要的速度越高；反过来，飞行速度一定时，间隙越小，极限环振荡的振幅越小，且间隙量增大1倍，极限环振荡的振幅近似增加1倍。

图7　极限环振荡的频率与振幅的关系

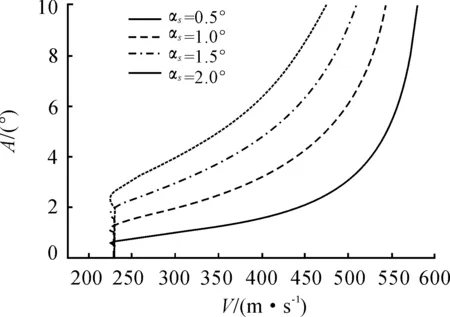
图8　间隙量对极限环振荡振幅-速度关系的影响

图9比较了kα1取不同值情况下极限环振荡的振幅与速度的关系。可见仅当kα1较小时，才会发生亚临界Hopf分叉；当kα1较大时，不会发生亚临界Hopf分叉，但当速度超过颤振临界速度时，舵面也会发生极限环振荡。由图9也可知，颤振临界速度随着kα1的增加并非单调地增加。图10给出了颤振临界速度随kα1变化的曲线。当kα1小于10 000 N·m/rad，颤振临界速度随kα1的增大而减小；而当kα1大于10 000N·m/rad，颤振临界速度随kα1的增大而增大。这主要是因为：如图11所示，当kα1小于10 000 N·m/rad，ωα/ωh随着kα1的增大而更接近于1，颤振速度减小；当kα1大于10 000N·m/rad，ωα/ωh随着kα1的增大而远离1，颤振速度增大。

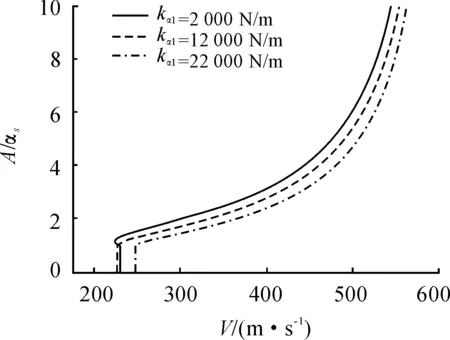
图9　间隙内的刚度对极限环振荡振幅-速度关系的影响

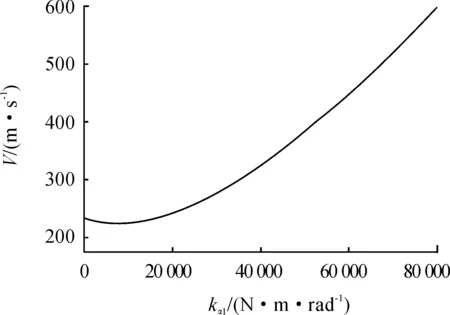
图10　间隙内刚度对颤振速度的影响

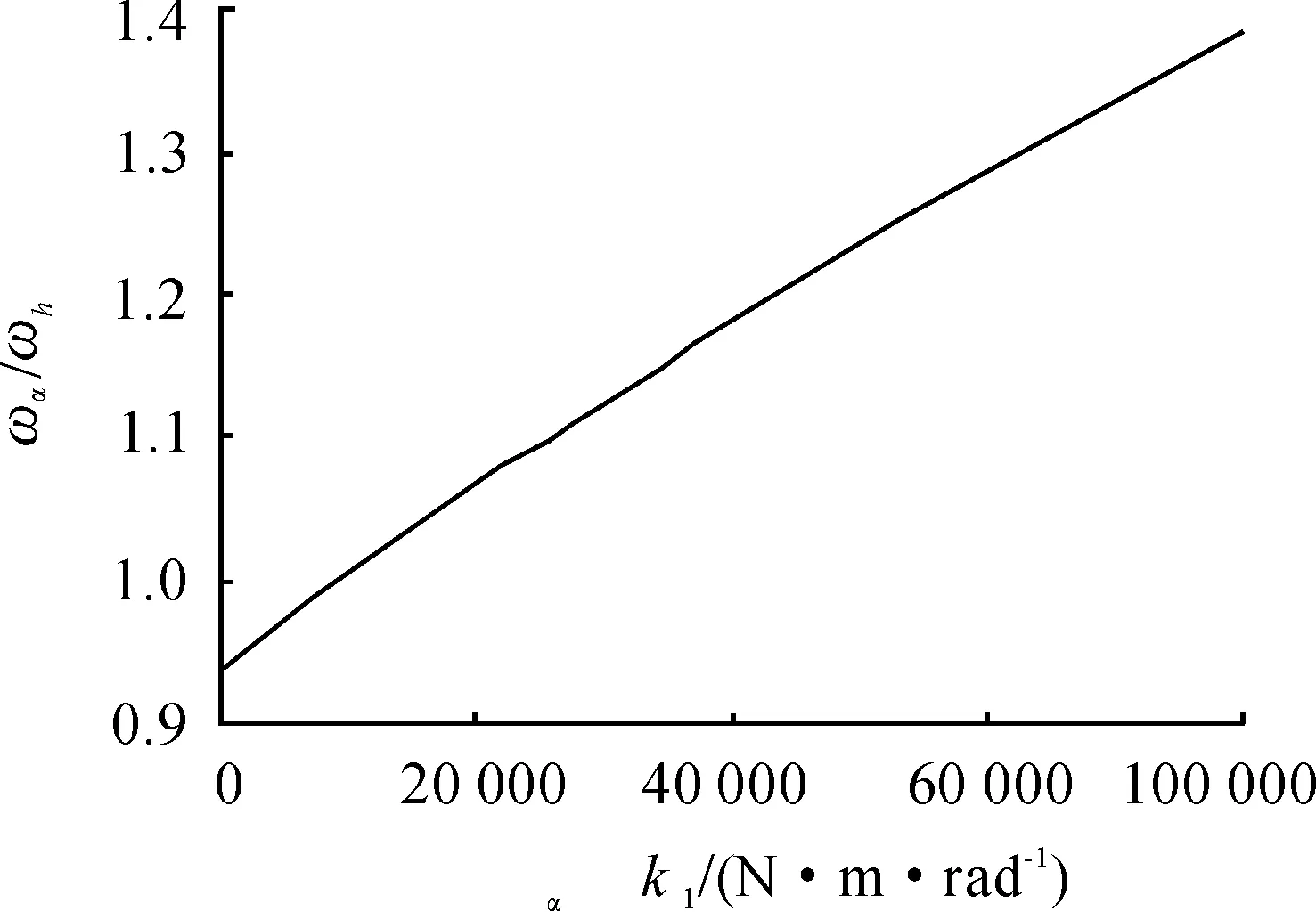
图11　间隙内刚度对俯仰/浮沉振动频率比的影响

3结论

本研究基于翼段模型和超声速活塞理论，考虑舵机传动机构的动力学特性和间隙非线性的影响，建立了俯仰方向含有间隙的舵面的非线性气动弹性动力学方程，利用Hopf分叉理论和描述函数法，对舵系统的气动弹性特性进行了理论研究。通过理论分析，给出了考虑舵机传动机构影响情况下的颤振速度方程，从而可以直接得出颤振速度与舵机传动机构参数的关系以及极限环振荡的振幅和频率与速度的关系。在此基础上深入讨论了舵机传动机构刚度和间隙非线性对气动弹性特性的影响。本研究得出如下结论：

1)当舵机的刚度较高时，考虑静刚度所预测的颤振速度与考虑动刚度得到的颤振速度差别很小；当舵机的刚度较低时，仅考虑舵机传动机构的静刚度所预测的颤振速度偏高，此时必须考虑舵机的动刚度，才能较准确地预测其气动弹性特性。

2)当振幅大于间隙αs时，等效线性刚度随着振幅的增大而增大。仅当间隙内的俯仰刚度kα1较小时，舵面的气弹响应才会发生亚临界Hopf分叉，即一旦速度超过亚临界分叉速度，即使小于线性颤振速度，舵面发生极限环振荡；当kα1较大时，不会发生亚临界Hopf分叉，但当速度超过线性颤振速度时，舵面也会发生极限环振荡。另外，在飞行速度一定的情况下，间隙量增大1倍，极限环振荡的振幅近似增加1倍。

参考文献：

[1]吴志刚，万志强，陈桂彬.飞行器气动弹性原理[M].北京：北京航空航天大学出版社，2011.

[2]CONNER M D,TANG D M,DOWELL E H,et al.Nonlinear aeroelasticity of an airfoil with control surface freeplay[J].AIAA Journal,97-0579.

[3]DOWELL E H,EDWARDS J,STRGANAC T.Nonlinear aeroelasticity[J].Journal of Aircraft,2003(40):857-874.

[4]LEE I,KIM S H.Aeroelastic of a flexile control surface with structural nonlinearity[J].Journal of Aircraft,1995,32(4):868-874.

[5]LEE B H K,LIU L,CHUNG K W.Airfoil motion in subsonic flow with strong cubic nonlinear restoring forces[J].Journal of Sound and Vibration,2005,281:699-717.

[6]LI D,XIANG J.Chaotic motions of an airfoil with cubic nonlinearity in subsonic flow [J].Journal of Aircraft,2008(45):1457-1460.

[7]LIU L,DOWELL E H.Harmonic balance approach for an airfoil with a freeplay control surface [J].AIAA Journal,2005(43):802-815.

[8]赵德敏,张琪昌,王炜.具有间隙非线性的二元机翼的随机分岔和功率谱分析[J].振动与冲击,2009,28(6):86-89.

[9]LAURENSON R M,TRN R M.Flutter analysis of missile control surfaces containing structural nonlinearities [J].AIAA Journal,1980,18(10):1245-1251.

[10]赵永辉,胡海岩.具有操纵面间隙非线性二维翼段的气动弹性分析[J].航空学报,2003,24(6):521-525.

[11]张军红,韩景龙.二元翼段间隙非线性颤振的模糊控制[J].振动与冲击,2012,31(6):58-61.

[12]贾尚帅,丁千.含间隙超音速二元弹翼非线性颤振与主动控制[J].中国科学:物理学 力学 天文学,2013,43(4):390-400.

[13]SHIN W H,LEE S J,LEE I.,et al.Effects of actuator nonlinearity on aeroelastic characteristics of a control fin [J].Journal of Fluids and Structures,2007(23):1093-1105.

[14]YANG N,WU Z G,YANG CH.Structural nonlinear flutter characteristics analysis for an actuator-fin system with dynamic stiffness [J].Chinese Journal of Aeronautics,2011(24):590-599.

[15]谷迎松,杨智春.带迟滞非线性环节二元机翼的气动弹性响应分析[J].机械科学与技术,2006,25(8):900-904.

[16]刘百慧,李敏,谭添才.具有结构非线性的二元翼面颤振研究[J].工程力学,2013,30(4):448-454.

[17]胡海岩.应用非线性动力学[M].北京：航空工业出版社，2000.

[18]赵永辉.气动弹性力学与控制[M].北京：科学出版社，2007.

(责任编辑杨继森)

【基础理论与应用研究】

Flutter Analysis of System of All Movable Fin with Freeplay Nonlinearity

ZHANG En-yang, SONG Rong-zhi, FENG Kun-cheng, LU Zhen-yu

(Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Science, Changchun 130033, China)

Abstract:The flutter characteristics of a fin of missiles system with freeplay nonlinearity in a supersonic flow were analyzed. Firstly, by adopting the typical section model and the piston theory and considering the dynamic properties of the transform mechanism of the fin system, the nonlinear aeroelastic dynamic equation of the fin with freeplay nonlinearity in the pitch degree of freedom was constructed. Then, the Hopf bifurcation theory and the describing function method were utilized to obtain the flutter velocity and the limit cycle oscillation response of the fin. The effects of the freeplay and dynamic properties of the transform mechanism on the flutter velocity and limit cycle oscillation (LCO) were investigated in detail. It is found that when the static stiffness of the transform mechanism is comparatively small, it is necessary to consider the effect of its dynamic stiffness on the flutter speed; only when the pitch stiffness within the freeplay is small, will the subcritical Hopf bifurcation phenomena happen and be at a fixed speed, and if the magnitude of freeplay doubles, the amplitude of LCO also approximately doubles.

Key words:freeplay nonlinearity; dynamic stiffness; flutter; limit cycle oscillation(LCO); Hopf bifurcation; describing function method

文章编号：1006-0707(2016)01-0136-07

中图分类号：V215.3

文献标识码：A

doi:10.11809/scbgxb2016.01.033

作者简介：张恩阳(1987—)，男，硕士，主要从事飞行器结构、机构研究。

收稿日期：2015-05-06；修回日期：2015-06-11