基于图像处理的红外成像设备畸变检测方法

吕俊伟，陈玉华，宋庆善

(1.海军航空工程学院 控制工程系, 山东 烟台　264001;

2.中国人民解放军91213部队装备部， 山东 烟台　264001)



基于图像处理的红外成像设备畸变检测方法

吕俊伟1，陈玉华1，宋庆善2

(1.海军航空工程学院 控制工程系, 山东 烟台264001;

2.中国人民解放军91213部队装备部， 山东 烟台264001)

摘要：红外制导导弹导引头、无人机光电载荷的核心部件是红外成像设备，红外成像设备能否正常工作决定了导弹和无人机的工作效能；为了避免红外导弹、无人机光电载荷带着故障上天，需要在这些装备上天之前检测红外成像设备是否工作正常，提出基于图像处理的图像畸变检测方法，作为判断红外成像设备工作正常与否的依据；以标准红外成像设备所成图像为标准图像，利用数字图像处理的边缘检测方法得出图像的面积和周长，根据面积和周长得出图像的复杂性参数值；在测试条件不变的情况下，根据罗曼诺夫斯基准则，利用正常设备捕获的图像作为样本，计算分析样本图像的面积和周长，求出图像复杂性参数值，得出红外成像系统测试的评价参数和评价准则，根据评价参数和评价准则判断被测试设备是否存在畸变。

关键词：红外成像设备；图像处理；畸变检测；复杂性；罗曼诺夫斯基准则

本文引用格式：吕俊伟，陈玉华，宋庆善.基于图像处理的红外成像设备畸变检测方法[J].兵器装备工程学报，2016(1):9-14.

Citation format:LYU Jun-wei, CHEN Yu-hua, SONG Qing-shan.Method of Testing Distortion of Infrared Equipments Imaging Based on Image Processing[J].Journal of Ordnance Equipment Engineering,2016(1):9-14.

红外制导导弹、无人机和侦察机等装备中的核心部件是红外成像设备。红外成像设备由于镜头内部机械过度磨损、变形、各个镜片发霉以及镜头电路问题等原因，会使图像不清晰、图像失真。如果无人机和导弹飞离地面后，才发现红外成像设备所成图像不清晰、失真等问题，捕获的图像达不到要求，甚至造成目标和背景丢失等捕获不到目标的严重问题，直接影响到设备对目标的侦察监视与定位的准确性，从而导致军事侦察活动失败或者打击不到目标，军事任务失败等严重后果。因此，在导弹、无人机和侦察机等装备飞离地面之前，必须对其红外成像设备进行检测。图像畸变程度是红外成像设备的一个评价标准，在红外制导导弹导引头和无人机光电载荷中检测红外成像设备的畸变程度，通过畸变程度可判断设备能否正常工作。在实验室条件下对红外成像设备进行检测，精度虽高但其过程复杂。基于此，在外场实地检测时，需要一种更快捷简便、更有效的畸变检测方法。

1检测原理

畸变表示点或线相对理想位置的偏移。根据畸变的常见类型分类，畸变可分为桶形畸变，枕形畸变和“S”畸变。由于设备镜头产生的畸变直接通过所成的图像反映出来，因此根据图像可判断成像设备是否存在畸变。在检测过程中，通过严格控制测试环境，测试条件，确保红外成像设备所成的图像收到噪声污染最少，且在前期处理中，利用相同的滤波方法滤除设备本身产生的固定噪声，这样，由于噪声等原因对设备检测准确性的影响将可以忽略，对测试结果准确性不会有太大影响。

在实验室通过判断靶标图像是否变形来判断是否存在畸变。选用双矩形靶标，使其测试图形应大于成像系统1/4 视场，以双矩形靶标所成图像作为为标准图像，以常见的桶形畸变、枕形畸变和“S”形畸变为测试设备要测试的内容，通过图像帧频采集卡获取图像，利用计算机对图像进行处理，根据图像计算出矩形面积值和周长值，计算对比分析数据值，以此判断成像系统是否存在畸变。首先，把标准设备放置到摄像机底座上，将其所成的图像作为标准图像存储到计算机硬盘中备份，然后将标准设备换成待测试设备，按照如图1所示结构图进行准备。

图1　畸变测试设备结构

2基于数字图像处理的红外成像设备畸变检测过程

测试时，将标准红外成像设备所成靶标图像输入计算机，对原始图像初步处理后，进行二值化处理，阈值M取最接近图像目标灰度值。因为选取的图像为双矩形靶标，目标显示图像为两个矩形，目标形状简单，容易分辨，而且目标用较高的温度，背景温度相对较低，控制测试时间测试条件，避免阳光直射目标，可见光对目标的影响可以忽略，这样就使得目标图像与背景形成了强烈对比，显示的图像边缘清晰，选择介于背景与目标之间的灰度值作为分割阈值，二值化时能把目标与背景完整分离开，如图2所示。

图2　红外靶标灰度图像二值化处理对比

对图像进行检测，需要知道能够表征图像形状特征的参数，用复杂性来表示。复杂性是用来描述目标形图形的复杂性的，参数值越大，表明图形形状越复杂。目标发生畸变，其周长和面积都跟随改变，但其变化趋势是图像形状越来越不规则，故可用复杂性来作为判定畸变的参数。

在同样条件下，更换待测试设备，将待测设备所成图像输入计算机，二者进行处理对比结果。流程如图3所示。

图3　畸变测试流程

测试过程可分3步：

第1步，获取目标二值图像，计算面积；

第2步，获取目标边框，计算周长，并计算出复杂度和畸变度；

第3步，利用复杂度和畸变度检测图像畸变。

2.1获取目标二值图像并计算面积

对图像进行二值化处理是接下来所有工作的前提。对采集得到的灰度图像以一定阈值M(M取决于灰度图像中目标部分的灰度值)将图像二值化，大于等于阈值M的点为1，小于阈值M的点为0。这样得到的图像就是灰度值为1的白色，灰度值为0黑白相间的二值化图像。二值化目的是为了把图像的目标明显地显现出来，得到一幅目标矩形为白色，目标背景为黑色的二值图像。

计算目标图像面积基本思想是：计算图像中的灰度值为1的像素个数，即白色像素的个数。但是在具体计算二值图像的面积过程中，不是简单计算像素值为1的像素个数，而是为每个像素设置一个权值，采用加权求和的方式得到面积。在计算二值图像的面积时，像素的权值，通过该像素的2×2的邻域像素值来决定。例如，如果邻域内的像素值都为0，则权值为0；如果邻域内的像素都为1，则权值为1。

采集的灰度图像，用相同方法进行二值化处理，对二值图像进行分析计算是检测的中心工作，为便于计算，后面，采用图像为已经经过二值化处理后的黑白图像。

2.2获得目标边框并计算周长

获取目标边框的的方法：对二值图像进行边缘分割。采用坎尼检测器(canny)边缘分割来获取图像的边缘。因坎尼检测器(canny)是迄今为止讨论过的边缘检测器中最优秀的。经过边缘检测后，图像变成两个白色矩形框，边框的宽度为1个像素。再利用加权求和的方式计算矩形和图像白色边框部分的面积，就是边框的周长。

2.3通过复杂性参数检测畸变图像

形状复杂性常用离散指数e表示，其计算式为

(1)

式(1)描述了单位面积图形的周长大小，e值大，说明单位面积的周长大，即图形离散，则为复杂图形，反之，则为简单图形。目标为双矩形靶标，畸变结果就是标准矩形变化成不规则的复杂图形。

标准设备和待测试设备所成的图像都根据2.1和2.2所示的原理来计算得到周长的面积。标准图像周长和面积用L和S来表示，畸变图像的周长和面积分别用Ln和Sn(其中n=1,2，…)表示。利用Ln和Sn计算图像的复杂性。利用复杂性的值计算图像畸变度，畸变度是值图像畸变的程度，用畸变图像复杂性与标准图像的差的比值表示。畸变度用Rn表示。计算式为

(2)

e为标准图像复杂性参数，en为待测图像复杂性参数。

取4幅图像，分别为标准图像，S形畸变图像、桶形畸变图像和枕形畸变图像，求出图像的面积、周长、复杂度和畸变度，结果如下：

标准图像：面积S：59 801，周长L：1433，复杂度e：34.34，畸变度R：0

S形畸变图像：面积S1：82 304,周长L1：2 057，复杂度e1：51.41，畸变度R1：0.497 1

桶形畸变图像：面积S2：113 250，周长L2：2 121，复杂度e2：39.72，畸变度R2：0.156 8

枕形畸变图像：面积S3：51 419，周长L3：1 488，复杂度e3：43.06，畸变度R3：0.254 0

将结果列表为(表1)：

表1　标准图像和畸变图像各参数对比

由表1可见，不同类型畸变其复杂度和畸变度都不相同，都大于标准图像的复杂度和畸变度。对于较明显的畸变，如图4，图5和图6所示，发现图像畸变严重，视觉对比明显。但在实际测试中这种结果是不那么容易出现的，对轻微畸变不明显，视觉对比不强烈的情形进行判别，就需要一个评价指标来判断图像畸变。

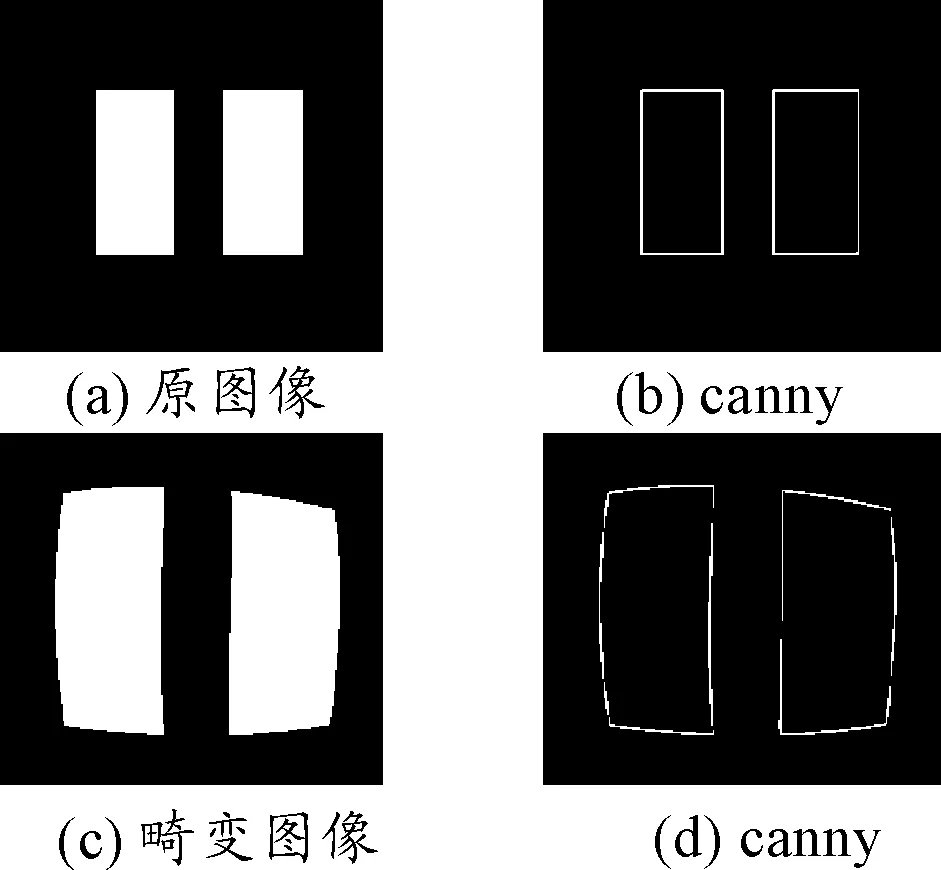
图4　桶形畸变图像对比

图5　枕形畸变对比

图6　“S”形畸变对比

3评价指标与评价准则的建立

选择评价指标，需要用统计规律，通过对大量的目标图像进行计算，并对计算结果进行分析统计。在实际情况下，无法用较多数量设备来进行一一测量。选择20个可正常工作的样本数据，根据罗曼诺夫斯基准则，用大误差判别方法求得σ值，即可得出结果。

3.1罗曼诺夫斯基准则

罗曼诺夫斯基准则是当测量次数较少时，按t分布的实际误差分布范围来判别粗大误差。罗曼诺夫斯基准则又称t检验准则，其特点是首先剔除一个可疑的测得值，然后按t分布检验被剔除的测量值是否含有粗大误差。

当测量次数较少时，按t分布的实际误差分布范围来判别粗大误差较为合理。罗曼诺夫斯基准则又称t检验准则，其特点是首先剔除一个可以的测得值，然后按t分布检验被剔除的测量值是否含有粗大误差。

设对某量作多次等精度独立测量，得

若认为测量值xj为可疑数据，将其剔除后计算平均值为(计算时不包括xj)

(3)

(4)

若

(5)

则认为测量值xj含有粗大误差，剔除xj是正确的，否则认为xj不含有粗大误差，应予保留。

表2　t 分布的检验系数K(n，α)

3.2建立评价参数与判定法则

设有n个样本测量值为

认为测量值xn+1为可疑数据，计算前n项平均值为

(6)

并求得测量列的标准差:

(7)

根据测量次数n和选取的显著度α，即可由表查得t分布的检验系数K(n，α)。

若

(8)

则认为测量值xn+1含有粗大误差，待测设备为不正常设备，否则认为xn+1不含有粗大误差，是正常设备，可以使用。

算法做法如下：

(11)

即

(12)

按照3.2的方法得出20组正常设备畸变的数据，为便于对比，把标准图像参数单独列表，其图像和列表(表3，表4)：

图7　畸变图像

面积S周长L复杂度e畸变度R标准图像59801143334.340

根据畸变率Ri计算Kσ，由表4计算出：

查表2，当n=20，取置信度α=0.5时，K=2.16,得,

Kσ=2.16×0.005 8=0.012 5

对畸变图像来说，畸变图像的畸变率超过0.012 5，即可判定为设别不能正常工作。

表4　畸变图像

4实验验证

下面利用3组目标图像来进行验证(图8)，图中第一行为标准图像与桶形畸变图像对比，第二行为标准图像与枕形畸变图像对比，第三行为标准图像与S形图像对比。

图8　验证正常设备图像和畸变图像对比

首先，得到3组二值图像，分别是正常设备图像和畸变图像，用来验证，(特别要说明的是，正常设备所成图像与标准设备的图像都是有误差的，其多少都存在畸变，而且畸变的类型也是3种畸变类型中的某一种，只不过是在要测试的正常设备相对于标准设备其畸变程度在误差范围之内，所以称为正常设备图像我们用畸变图像1来代表)如图8所示。

根据3.3可以算出3组畸变图像的复杂度和畸变度，在Matlab中编程计算，运算结果如表5所示。

由3.2.1节中畸变的判定法则，畸变度超过0.012 5，即可判定为设别不能正常工作。

要验证的3组图像如下：

桶形畸变图像1，其畸变度R1=0.006 351 481 < 0.012 5,该图像合格；

桶形畸变图像2，其畸变度R2=0.021 547 426 > 0.012 5,该图像不合格；

枕形畸变图像1，其畸变度R3=0.010 008 815 < 0.012 5,该图像合格；

枕形畸变图像2，其畸变度R4=0.078 256 525 > 0.012 5,该图像不合格；

S形畸变图像1，其畸变度R5=0.011 202 038 < 0.012 5,该图像合格；

S形畸变图像2，其畸变度R6=0.082 034 478 > 0.012 5,该图像不合格。

利用判定法则判定图8第二列图像，即桶形畸变图像1、枕形畸变图像1和S形畸变图像1都为合格，且看不出有畸变，而第三列图像，桶形畸变图像2、枕形畸变图像2和S形畸变图像2都为不合格，用人眼也可分辨出这3组图像都有畸变。判定法则与人眼判定结果一样，且有较高准确度。

实验分析：

在求解评价参数过程中，式(1)～式(11)中均值使用的标准图像的复杂度值，而不是用样本值的期望值，因为标准图像的值是最为精确的，可作为真值处理，而待测设备因为其生产批次、存放条件等原因不同所造成的误差也不同，但如果待测设备数量趋于无穷大时，其所有图像复杂度的期望的极限就是标准图像的复杂度值即真值。使用标准图像的复杂度就是排除批次不同等原因而对测试条件的影响，从而保证了测试结果的准确度，同时便于计算。

表5　3组畸变图像复杂度和畸变度结果数据对比

5结论

利用数字图像处理方法，通过对图像的面积和周长进行测量，计算出复杂度和畸变度，并与判定指标相比较，判别红外成像设备是否有畸变，方法简便快捷，有较高的准确度。当然该方法也有其局限性，即只能判定设备是否有畸变，如果需要对设备畸变的原因及程度进一步判断或者对畸变图像需要校正等进行进一步处理和判断还需要深入研究，再者，该方法是通过数理统计的方式得出评价参数，以较高的准确率判别是否存在畸变，但如果需要更高精度的判断，还需要进一步的研究探索。

参考文献：

[1]王晓蕊，张建奇，冯卓祥，等.采样红外成像系统仿真及最小可分辨温差预测方法研究[J].红外与毫米波学报，2004,23(6)：436-440.

[2]魏建强.红外成像器通用测试技术及标准设备概述[C]//中国宇航学会.第三届红外成像系统仿真、测试与评价技术研讨会论文集.浙江宁波：中国宇航学会，2011：51-57.

[3]李艳晓，胡磊力，蔡猛.红外成像系统的性能测试方法研究[J].红外与激光工程，2008，37(6):449-454.

[4]RAFACL C.Gonzalez,Richard E.Woods.数字图像处理[M].3版.阮秋琦，阮宇智,等，译.北京：电子工业出版社，2013：93-96,443-467.

[5]费叶泰.误差理论与数据处理[M].6版.北京：机械工业出版社，2010：46-47.

[6]方如明，蔡建荣，许俐.计算机图像处理技术及其在农业工程中的应用[M].北京：清华大学出版社，1999:88-90.

[7]CEHN Baoguo,FAN Yangyu,ZHANG Xuefeng,et al.Moving scene based nonuniformity correction algorithm[C]//Proceeding of SPIE,2012,8419:84191Q-1-84191Q-6.

[8]王洋，谢权威.基于相机响应函数的图像盲检测技术研究[J].重庆工商大学学报(自然科学版)，2014，31(3)：55-61.

[9]刘书琴，毋立芳，宫玉.图像质量评价综述[J].中国科技论文在线，2011，6(7):501-523.

(责任编辑周江川)

【装备理论与装备技术】

Method of Testing Distortion of Infrared Equipments Imaging

Based on Image Processing

LYU Jun-wei1, CHEN Yu-hua1, SONG Qing-shan2

(1.Department of Control Engineering, Naval Aeronautical Engineering Institute, Yantai 264001, China;

2.Equipment Department, the 91213rdTroop of PLA, Yantai 264001, China)

Abstract:Infrared imaging equipment is the core component of IR guided missile seeker and UAV, and the work efficiency of missile and UAV can be determined by infrared imaging equipment. It is necessary to detect whether the infrared imaging equipment is normal or not, in order to avoid the fault with which IR guided missile seeker and UAV flying into the sky. So a method of image distortion detection based on image processing was proposed. The standard infrared imaging equipment for imaging was supposed as the standard image, and the digital image processing edge detection method was used to draw the area and perimeter of the image, and the complexity parameter values of the image were calculated according to the area and perimeter. Then under the same test conditions, according to the idea of Romanowski criterion, normal devices to capture images as samples were used to the calculation and analysis of the area and perimeter and the parameter values of the complexity of the images as samples. Test of infrared imaging system of evaluation parameters and evaluation criteria were derived. According to the evaluation parameters and evaluation criteria, the device being tested was judged whether there is a distortion.

Key words:infrared imaging equipment; image processing; distortion of test; complexity; Romanowski criterion

文章编号：1006-0707(2016)01-0009-06

中图分类号：TJ765.4

文献标识码：A

doi:10.11809/scbgxb2016.01.002

作者简介：吕俊伟(1960—)，男，教授，博士生导师，主要从事目标识别与智能系统、目标探测与跟踪等研究。

基金项目：国家自然科学基金(61032001；60801049)

收稿日期：2015-06-27；修回日期：2015-07-20