低速旋转弹丸偏流现象数值模拟

何　颖，胡金波，邹　亚，孙　凯

(南京理工大学 瞬态物理重点实验室，南京　210094)



低速旋转弹丸偏流现象数值模拟

何颖，胡金波，邹亚，孙凯

(南京理工大学 瞬态物理重点实验室，南京210094)

摘 要：以三维N-S方程为基础，运用滑移网格技术，采用标准k-ε湍流模型，对低速旋转弹丸在不同转速和攻角条件下的绕流流场进行了数值模拟，从流场结构和气动特性方面对低旋弹丸的偏流现象产生机理进行了分析，给出了弹丸侧向受力及周向压力分布规律，并对影响偏流现象的因素进行了验证。

关键词：低速旋转炮弹；偏流；数值模拟；滑移网格

本文引用格式：何颖，胡金波，邹亚，等.低速旋转弹丸偏流现象数值模拟[J].兵器装备工程学报，2016(1):18-22.

Citation format:HE Ying, HU Jin-bo, ZOU Ya, et al.Numerical Simulation of Deflective Flow for the Low-Speed Revolving Cannonball[J].Journal of Ordnance Equipment Engineering,2016(1):18-22.

弹丸低速旋转飞行可以带来许多好处，例如，可以减小推力偏心、质量偏心、气动偏心等非对称因素对飞行特性的影响；能够简化控制系统，为导弹小型化提供方便。然而，弹丸在旋转过程中由于纵轴与速度方向不重合，往往使得其外形上的空气动力载荷呈现出不对称分布，从而激发出一些新的非常规的力和力矩，影响射击精度甚至使得飞行失常[1]。低速旋转弹丸在发射后其落点往往会偏离射击面，并且右旋弹偏右，左旋弹偏左。人们很长一段时间都解释不了这一现象，直到发现了偏流，由于动力平衡角的存在，使得弹丸在飞行过程中的实际弹道偏离了初始射击平面。

目前，通过调节偏流的大小来实现侧向弹道修正已受到广泛关注[2-5]，对偏流的近似计算也提出了一些方法[6-8]。但是基于偏流现象的数值模拟研究做得较少。文献[9]中采用了滑移网格技术对高速旋转弹丸进行了数值模拟，其结果与实验数据符合很好，表明滑移网格技术在模拟旋转绕流时具有较高的计算精度，因此，本研究应用滑移网格技术模拟了不同攻角和转速条件下低速旋转炮弹的绕流流场，并从流场结构和气动特性方面对偏流现象的产生机理以及影响因素进行深入分析。

1低速旋转炮弹偏流现象的基本原理

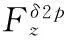
(1)

(2)

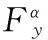
(3)

(4)

由外弹道理论可知[7]，在影响旋转稳定炮弹侧向运动的作用力中，Magnus力在速度坐标系内的侧向分量相对于升力分量较小，因此由动力平衡角产生的侧向升力分量是引起偏流的主要作用力。

图1　偏流原理示意图

图2　动力平衡角产生Magnus效应示意图

2计算方法与数值模型

2.1数值方法

本研究以三维Navier-Stokes方程为基本方程，湍流模型采用Standardk-ε模型，由于该模型中ε方程包含不能在壁面计算的项，因此必须使用壁面函数，本研究采用的是标准壁面函数法，标准壁面函数法能够在计算量较小的情况下得到较高的精度。

弹丸的旋转通过滑移网格模型来实现。滑移网格技术要求存在一个外部固定区和包围弹体的内部运功区，两个运动区之间具有一对交界面，交界面上的网格节点不需要重合，只需要在滑移交界面上进行数值差值，即可保证两个区域之间的通量守恒，且内部运动区的网格单元在运动过程并不发生变形，因而滑移网格技术占用内存小，计算速度快，精度高。

2.2计算模型

本文计算外形为三维卫星制导迫弹，如图3所示。计算条件如下：

1) 马赫数Ma=0.8，总温T0=300 K，总压P0=101 325 Pa；

2) 转速ω=0,10,30 r/s，从弹尾向头部看去逆时针旋转；

3) 攻角α=0°,4°,6°,8°,10°,12°；D为弹径，L为弹长(m)。

图3　几何模型

2.3计算网格及边界条件

采用ICEM CFD软件进行结构化网格划分，计算区域分为外部固定区和内部运动区，图4为弹体表面的网格示意图，图5为对称面内弹体附近的网格示意图。

图4　弹丸表面网格分布图

图5　弹体附近网格示意图

弹体表面采用转动壁面边界条件，转动形式与相邻区域关联，对应的速度值为0，表明弹体和其相邻区域同步转动；内部运动区域采用滑移网格边界条件；外部固定区域采用压力远场边界条件；通过合并内外区域的交界面使得两侧的数据进行插值传递。

3数值模拟结果

3.1不同攻角和转速条件下的流场结构

图6、图7和图8为转速ω=0和30，攻角α=0°和12°时不同截面处的压力等势分布。由图6(a)、7(a)和8(a)可知，当转速和攻角都为0时弹体周围压力呈对称分布；图6 (b)和图6 (c)为不同转速时攻角平面的压力等势分布，从图6中可知，当攻角α=12°时，在攻角平面内产生了上下压力不对称分布，迎风面压力升高背风面压力减小，弹体头部产生向上的升力，尾部产生向下的升力抑制弹体抬头，由于全弹迎风面的压力大于背风面，因此弹体受到向上的升力。

图7(b)和图7(c)为不同转速时弹体x/L=0.35横截面(中部)的压力等势分布。从中可以看出，当ω=0时，弹体左右两侧压力分布对称；当ω=30时弹体左侧压力低于右侧压力，弹体受到向左的侧向力。图8 (b)和图8 (c)为不同转速时弹体x/L=0.95横截面(尾翼)的压力等势分布，由图可知，α=12°时尾翼下表面压力高于上表面，尾翼处产生向上的升力；图8(a)和图8(b)中，ω=0时尾翼左右两侧压力为对称分布，不产生侧向力；而在图8(c)中ω=30时左侧压力低于右侧压力，产生向左的侧向力。

图9为弹体不同截面的三维马赫等值图。由图9 (a) 、图9 (b)可知，当ω=0时，弹体周围边界层相对与攻角平面对称；由图9(c)可知，ω=30时边界层发生了偏移，左侧边界层变薄右侧边界层变厚。这是由于弹丸在左旋过程中，动力平衡轴逐渐偏移产生了向左的动力平衡角，使来流产生了向左的升力分量。

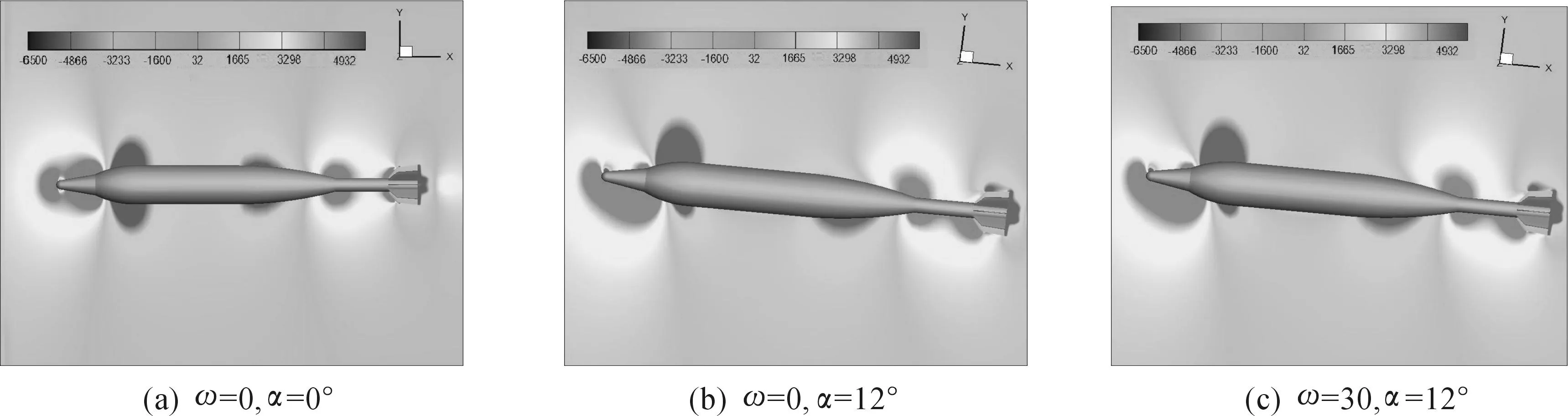
图6　攻角平面(z=0)压力场等势分布(Ma=0.8;ω=0,30; α=0°,12°)

图7　弹体中部(x/L=0.5) 压力场等势分布(Ma=0.8; ω=0,30; α=0°,12°)

图8　尾翼处(x/L=0.95)压力场等势分布(Ma=0.8; ω=0,30; α=0°,12°)

图9　弹体不同截面处马赫等值图(Ma=0.8; ω=0,30; α=0°,12°)

3.2侧向力和力矩系数模拟结果

图10和图11分别为不同转速时全弹侧向力系数和侧向力矩系数随攻角变化曲线，图12为ω=30时弹体不同部位的侧向系数随攻角的变化曲线。

由图10可知，当攻角为0°时，不同转速条件下的侧向力系数都为0，这是由于旋成体的对称性造成的；当转速为0时，侧向升力几乎不受攻角的影响，几乎为0；当且仅当攻角和旋速同时不为0时，弹体产生了侧向升力，且升力系数随攻角和转速增大而增大。

由图11可知，弹丸旋转时侧向力矩系数随着攻角的增大先增大后减小，8°攻角时为转折点。从图12中可以看出，弹体中部受到的侧向力最大，且随攻角增大而增大的变化趋势明显；头部因受侧向力而轻微摆动；尾部受到的侧向力有先增大后减小的趋势。其原因可能是攻角越大，弹体受到向上的升力分量越大，由于惯性作用使得旋转对弹体运动的改变越难。

图10　侧向升力系数随攻角变化曲线

图11　侧向力矩系数随攻角变化曲线

图12　弹体不同部位的侧向力系数随攻角变化曲线

图13为不同攻角时侧向力系数随转速变化曲线，可知，弹丸受到的侧向力与攻角和转速成比例关系，转速越大，弹丸受到的侧向力越大。

图13　侧向力系数随转速变化曲线

3.3弹体表面压力分布

图14为ω=0,30时弹体左右两侧(即δ=0°，180°)表面压力沿轴向分布，从图14中可以看出，ω=0时弹体左右两侧压力曲线几乎重合，弹体没有偏流；ω=30时弹体中部明显压力不平衡，左侧压力低于右侧，弹体向左侧偏移。

图15分别为弹体不同横截面的周向表面压力分布曲线。从图15(a)可知，弹体头部(x/L=0.15)迎风面的压力远高于背风面，受到较大的升力，左右两侧的压力没有明显差异；由图15(b)可知，弹丸旋转时中部(x/L=0.35)左右两侧产生了压力差，左侧压力低于右侧；从图15(c)可知，尾部(x/L=0.6)受到了一个向下的升力以抑制弹体的抬头，旋转时左侧压力低于右侧压力。

图14　弹丸左右两侧的轴向表面压力分布曲线

图15　 弹体不同横截面的周向表面压力分布曲线

4偏流现象的影响因素

由文献[4，8]可知，方向动力平衡角与弹体的转速成比例关系，文献[10]中通过弹道仿真证明了发射速度越大，弹丸受到偏流的影响越小。为此，采用不同来流速度和转速条件进行仿真，对影响偏流大小的因素进行了数值验证。

针对研究的弹型，补充超音速和高转速条件下的流场计算，验证来流马赫数与转速对偏流的影响。表1为不同来流马赫数和转速条件下的侧向力(矩)系数和侧向力的方向。从表1中可以看出，在Ma=0.8,ω=30时，弹丸产生了偏向旋转方向的侧向力，增大转速到200 r/s时，偏流更明显，这是因为转速增大使得弹丸轴向动量矩加大，弹轴的定向性增强，为使弹轴追随弹道切线下降的动力平衡角增大，从而使得侧向升力和偏流增大。在转速不变的情况下增大来流马赫数(Ma=2.5,ω=30)，侧向力的方向发生改变(与Magnus力方向一致)；在超音速时弹丸高旋(Ma=2.5,ω=318)，则产生较大的Magnus力。从上面的数据可知，在来流马赫数相对于转速不大的情况下，弹丸的旋转更容易使得弹丸偏离原来的飞行状态；而当弹丸的飞行速度相对于转速较大时，产生的惯性也大，使得要改变原来的飞行状态就越难。

表1　不同来流马赫数和转速条件下的

5结论

本研究基于N-S方程和滑移网格技术对低速旋转弹丸的绕流流场进行了数值模拟，分析了低旋弹丸在飞行过程中偏流的产生机理以及影响偏流的原因，得出了以下初步结论：

1) 弹丸在低速旋转飞行过程中，会产生偏向旋转方向的偏流，且弹体中部受到的侧向力最大；

2) 当Ma增大，ω减小的时候，偏流减小；反之则偏流增大。且当Ma增大到一定值时，侧向力方向可能改变。

参考文献：

[1]苗瑞生,吴甲生.旋转弹空气动力学[J].力学进展,1987,17(4):479-487.

[2]GRIGNON C,CAYZAC R,HEDDADJ S.Improvement of projectile accuracy[Z].Tarragona,Spain:IBC,2007：747-754.

[3]FRESCONI F,PLOSTINS P.Control mechanism strategies for spin-stabilized projectiles [R].Maryland,USA:US Army Research Laboratory,AD-A494194,2008.1-25.

[4]史金光,王中原,常思江,等.二维弹道修正弹修正方法[J].海军工程大学学报,2010,22(4):87-92.

[5]常思江,王中原,史金光,等.基于偏流调节的横向弹道修正方案有效性分析[J].南京理工大学学报:自然科学版,2013,37(4):573-578.

[6]王欣,姚俊.低速旋转火箭弹飞行弹道偏流分析[J].沈阳理工大学学报,2004,23(3):79-81.

[7]宋丕极.偏流的近似计算与分析[J].弹道学报,1990(3):45-50.

[8]韩子鹏.弹箭外弹道学[M]．北京:北京理工大学出版社,2008:176-180．

[9]雷娟棉,李田田,黄灿.高速旋转弹丸马格努斯效应数值研究[J].兵工学报,2013,34(6):718-725.

[10]蓝志环,田春艳,车继馨,等.低速旋转炮弹偏流现象的研究[J].科学技术与工程,2011(26):6456-6462.

(责任编辑周江川)

【装备理论与装备技术】

Numerical Simulation of Deflective Flow for

the Low-Speed Revolving Cannonball

HE Ying, HU Jin-bo, ZOU Ya, SUN Kai

(Key Laboratory of Transient Physics, Nanjing University of Science & Technology, Nanjing 210094, China)

Abstract:Based on the 3-dimension N-S equation, simulation of flow field over a low-speed spinning projectile at different rotate speed and angle of attack were carried out by using the standard k-ε turbulence model. Spinning was implemented through sliding mesh method. the generated mechanism of deflective flow for the low-speed revolving cannonball were analyzed by the flow field structure. Through numerical simulation, the lateral force and pressure coefficient along the cylinder’s surface were presented, and at last the influential factors of the deflective flow phenomenon were analyzed.

Key words:low-speed revolving cannonball; deflective flow; numerical simulation; sliding mesh

文章编号：1006-0707(2016)01-0018-06

中图分类号：TJ156；TJ4

文献标识码：A

doi:10.11809/scbgxb2016.01.004

作者简介：何颖(1987—)，女，博士研究生，主要从事兵器科学与技术研究。

基金项目：总装基金(9140C3007081005)

收稿日期：2015-07-09；修回日期：2015-08-08