对圆锥曲线一个统一性质的再思考



对圆锥曲线一个统一性质的再思考

北京市陈经纶中学(100020)王小平张留杰

文[1]中给出了圆锥曲线的一个漂亮的统一性质：

性质若圆锥曲线E上某点P的法线与对称轴(抛物线指对称轴，双曲线指实轴，椭圆指长轴)交于点G，过点G作焦半径的垂线l，垂足为L，则PL的长度为圆锥曲线的正焦弦长的一半．

笔者发现，借助圆锥曲线的光学性质可以对此性质进行简证，并且还可以将结论更加完善，现与大家分享．

性质1如图1，若抛物线y2=2px(p>0)上一点P的法线与x轴交于点G，过点G作焦半径PF的垂线，垂足为L．则PL=p．

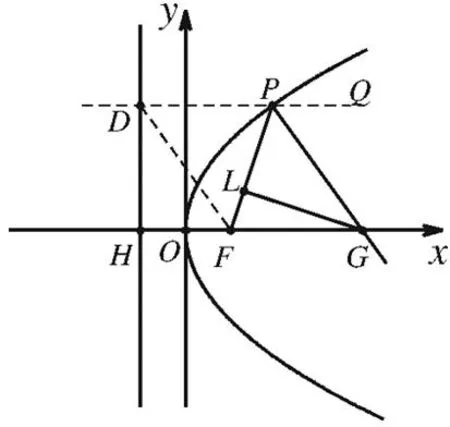
图1

证明：设抛物线的准线交x轴于点H，过点P作直线PQ∥x轴，交抛物线的准线于点D，连结DF．∵PG为法线，由抛物线的光学性质，得∠GPF=∠GPQ，又∠GPQ=∠FGP，∴∠GPF=∠PGF，∴FP=FG．由抛物线的定义得FP=PD，∴FG=PD，∴四边形FGPD为平行四边形，∴GP=FD，又∠GPL=∠PGF=∠DFH，∠GLP=∠DHF=90°，∴Rt△GPL≌Rt△DFH，∴PL=FH=p．

图2

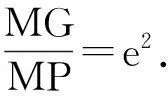
同理，在双曲线中也可以得到：

图3

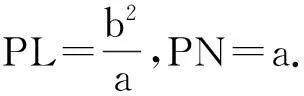
(类比性质2，结论不难证明，读者可以自行完成．)

综合性质1,2,3可得：

圆锥曲线的一个优美性质

(1)若有心圆锥曲线E上一点P的法线与经过焦点的对称轴交于点G，与另一条对称轴交于点M，过点G、M分别作焦半径PFi(i=1,2)所在直线的垂线，垂足分别为L、N，则线段PL等于圆锥曲线的正焦弦的一半，PN等于圆锥曲线的长轴(双曲线时为实轴)的一半．

(2)抛物线C上一点P的法线与其对称轴交于点G，过点G作焦半径的垂线，垂足为L，则PL等于抛物线的正焦弦的一半(或者抛物线的焦准距)．

参考文献

[1]刘立伟.圆锥曲线中一组漂亮的统一性质.数学通讯，2012(9)(下半月)．

[2]圆锥曲线的光学性质及其应用.普通高中课程标准实验教科书《数学(选修2-1)》A版，第75页.人民教育出版社．2012.6.