具有变系数的高阶时滞差分方程的有界振动

杨禹慧

（吕梁学院数学系,山西吕梁033000）

具有变系数的高阶时滞差分方程的有界振动

杨禹慧

（吕梁学院数学系,山西吕梁033000）

研究一类具有变系数的高阶差分方程Δd［x（t）＋b（t）x（t－τ）］－q（t）x（t－σ）＝0,0＜t0≤t＜＋∞有界解的振动性,给出有界解振动的充分条件.

差分方程；有界解；振动；最终正解

1 概述

差分方程的振动性研究作为差分方程程定性理论研究的一个分支,已受到学者的广泛关注与研究.目前关于差分方程的解的性质的研究已经比较广泛,这几年来,对于高阶中立型时滞差分方程振动性的研究也得到了许多结果.关于具有连续变量的高阶差分方程的有界振动的研究,可见文献［1－4］.

在文献［5］中,黄梅等研究了具有变系数的高阶中立型时滞差分方程,即

的解的振动性,其中l为奇数,本文在此基础上重新对d进行设定,用新的方法研究一类更为广泛的具有变系数的高阶时滞差分方程即

的解的振动性.其中：d为正整数,这里假设且q（t）为不恒为0的有界函数,令其中τ,t0,σ是给定的非负实数,σ＝kτ,k为某个正整数.Δx（t）＝x（t＋τ）－x（t）,Δ2x（t）＝Δ（Δx（t））.我们总假设方程（1）存在解.方程（1）的一个有界解｛x（t）｝称为振动的,如果它最终既不为正,也不为负,否则称为非振动的.若方程（1）的每一个有界解｛x（t）｝都是振动的,称该方程为振动的.

2 基本引理

引理1［1］假设d≥1是整数,｛z（t＋nτ）｝是实数列,如果｛Δdz（t＋nτ）｝最终定号（即当n充分大后恒有｛Δdz（t＋nτ）｝＞0或有｛Δdz（t＋nτ）｝＜0）,则｛Δiz（t＋nτ）｝最终严格单调且定号（i＝0,1,2,…d－1）.

引理2［2］设z（n）＞0（n≥a）,Δpz（n）（n≥a）定号且不为0,则存在整数j（0≤j≤p）,对于Δpz（n）≤0,p＋j为奇数；对于Δpz（n）≥0,p＋j为偶数.使对n≥a有：（a）若j≤p－1,则（－1）i＋jΔiz（n）＞0,j≤i≤p－1；（b）若j≥1,则Δiz（n）＞0,1≤i≤j－1.

3 主要结果

定理1 假设d≥1且为正整数且－1≤b（t）＜b,（－1≤b＜0）；若x（t）为方程（1）的最终有界正解,令z（t）＝x（t）＋b（t）x（t－τ）,则最终成立

由条件可知Δdz（t）不恒为0,故Δd－1z（t）必最终为正或最终为负.进而推出Δd－2z（t）,…Δz（t）都最终为正或最终为负.

假设Δd－1z（t）＞0.则存在t2≥t1且j≥1时有

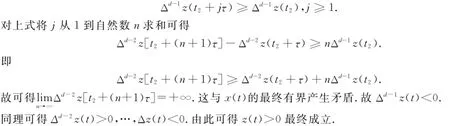
定理2 方程（1）如果满足下列条件

则方程（1）的有界解是振动的.

证明：对于研究方程（1）的有界解x（t）的振动性问题,下面我们对d分情况进行讨论：

1）当d≥2且为偶数时：

设x（t）为方程的有界正解且满足x（t）＞0,x（t－τ）＞0,x（t－σ）＞0,t≥t1≥t0.

根据条件（H2）我们可知存在t¯≥t1≥t0,当t≥t¯≥t1≥t0时有

这与（4）式矛盾,故当d为偶数且d≥2时,方程（1）的所有有界解振动.

2）当d≥1且为奇数时,假设x（t）为方程的有界正解.令z（t）＝x（t）＋b（t）x（t－τ）,则方程（1）变为

故Δd［z（t）］＝q（t）x（t－σ）＞0.由引理及定理1可得：｛Δiz（t）｝单调定号（i＝.,1,2,…,d－1）且z（t）＞0.我们假设T则T≥0.

故产生矛盾.

所以当d≥1为奇数时,方程（1）的所有有界解振动.

综上所述方程（1）的有界解是振动的.

［1］唐 清,干曾玲.高阶中立型差分方程的振动性及其非振动解的渐进性态［J］.数学杂志,2000,20（2）：207－210

［2］Agarwal R P,Difference Equations and Inequalities［M］.New York：Marcel Dekker,1992

［3］杨甲山,李继猛.具有连续变量的高阶非线性差分方程的振动与非振动准则［J］.合肥工业大学学报（自然科学版）,2010,33（6）：934－938

［4］刘一龙,杨甲山.具有连续变量的奇数阶时滞差分方程的振动准则［J］.合肥工业大学学报,2009,32（4）：591－593

［5］黄 梅.具变系数的高阶中立型时滞差分方程的振动性［J］.湖南第一师范学院学报,2016,16（2）：95－96

［6］杨甲山,李继猛.具有连续变量的高阶非线性差分方程的振动与非振动准则［J］.合肥工业大学学报（自然科学版）,2010,33（6）：934－938

［7］赵良鹏,闫卫平.带有强迫项的高阶差分方程解的振动性［J］.郑州大学学报（理学版）,2014

［8］杨禹慧,赵良鹏.具连续变量的高阶非线性差分方程的有界振动［J］.贵州师范大学学报（自然科学版）,2016,34（2）：52－55

Bounded Oscillation for a Class of Higher Order Difference Equation with Variable Coefficients

YANG Yuhui
（Department of Mathematics Lvliang University,Lvliang 033000,China）

Bounded Oscillation for a class of High－Order difference Equations

1672－2027（2016）04－0009－04

0175

A

2016－08－21

杨禹慧（1987－）,女,山西吕梁人,硕士,吕梁学院助教,主要从事常微分方程研究.