多机协同的组网雷达欺骗干扰航迹优化*
2016-02-24李小波孙琳周青松单凉
李小波,孙琳,周青松,单凉
(电子工程学院,安徽 合肥 230037)
导航、制导与控制
多机协同的组网雷达欺骗干扰航迹优化*
李小波,孙琳,周青松,单凉
(电子工程学院,安徽 合肥 230037)
针对组网雷达抗欺骗干扰能力强的特点,分析了三维空间利用多机协同对组网雷达进行航迹欺骗的可行性。首先从几何关系上分析了飞行器完成欺骗干扰的运动条件,并提出了优化干扰航迹的数学模型。利用该模型可以提高假航迹的干扰成功概率并且使干扰机飞行过程推力最小化,最后通过仿真实验证明了优化模型的可行性。
多机协同;欺骗干扰;组网雷达;航迹优化;数字射频存储;最小推力
0 引言
现代战争,敌我双方围绕雷达与雷达对抗装备[1-2]间的斗争愈演愈烈。组网雷达[3]凭借其多频段、多体制及信息融合的优势,使得传统欺骗干扰难以达到理想干扰效果,而利用多无人机协同干扰,可以将分布式干扰及空间航迹融合[4-5]的优势充分发挥,达到欺骗目的,在敌方的雷达网信息融合系统中形成欺骗干扰航迹,迫使敌方加强空情处置,调动其战略部署。
多飞行器协同欺骗干扰技术作为较新的研究领域,得到了相关学者的研究,陆续的提出了多机协同干扰方法。Mclain[6]等人于2000年研究提出了多机协同的汇聚问题,利用泰森多边形汇聚原理,使多无人飞行器在确定时刻在雷达网内的暴露点迹最小化,从而达到控制飞行路线及飞行方向的目的;K. B. Purvis[7-8]在总结前人方法的基础上,对于多机协同欺骗进行了更深入的研究,首先利用多机协同对网内雷达的位置进行确定,然后根据雷达位置提出了基于瞄准线准则的协同欺骗算法,考虑了风向以及油耗对于整个飞行系统的影响。对于多机干扰系统,引入代价函数是为了更好的对假目标航迹及飞行器运动状态进行优化,然而文献[9-10]将假目标及飞行器的运动状态统一到同一代价函数中,参数较多,优化维数庞大,不能够起到良好的优化效果,甚至部分模型速度抖动过于剧烈,在现实情况下不可能完成干扰任务。
针对前人研究局限于二维空间且对于优化问题分析不够透彻的缺点,提出了更加合理的优化指标。在确保较为简捷的完成干扰任务的同时,最大限度的提高干扰效率及空间容错率,经过仿真证明本文所提方法的有效性及合理性。
1 多机协同欺骗干扰的基本原理及数学模型
1.1 基本原理
利用飞行器对雷达网进行欺骗的基本原理就是将不同干扰飞机分别对网内的雷达进行距离延时干扰, 延时干扰后的目标融合为同一目标。如图1所示,干扰机对接收到的雷达脉冲信号进行延时转发,经过转发后的脉冲信号由雷达主瓣进入信号处理系统,形成假目标。
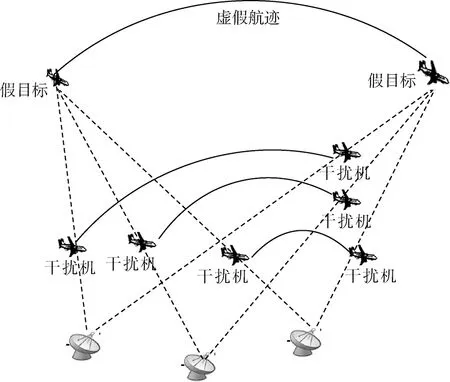
图1 多飞行器干扰雷达网示意图Fig.1 Deception jamming against radar network using UAVs
完成整个干扰过程需要达到以下条件:①干扰平台运动状态可控,整个假航迹的形成过程需要干扰飞机通过运动状态的控制进行配合确保虚假点迹融合成功;②雷达位置可知,在干扰过程中,可利用多干扰机的时差定位确定雷达位置,从而实施精确地延时干扰;③干扰机平台隐身化,干扰机平台的隐身化有利于干扰实施过程中的安全,不被敌方发现,确保干扰过程完整顺利。利用小型无人机平台“低慢小”的特点躲避敌方雷达的侦察干扰,顺利完成整个干扰流程;④干扰机可对相应雷达进行转发式干扰,利用数字射频存储(digital radio frequency memory,DRFM)技术[11-12]转发式干扰,可以快速识别转发所接收的雷达信号,保证对雷达网成功进行欺骗。
多机干扰的实现流程如图2所示。信息获取模块首先需要获取雷达内各雷达位置及雷达的参数信息; 专家决策系统决定飞行器及假目标的起始位置,控制飞行器及相应的转发时延,使假目标完成融合;代价模型计算模块根据此刻的飞行器及假目标的位置,计算出下一时刻飞行器所处的最优位置,专家决策系统根据最小代价及完成任务的可行性进行综合处理,分析并传达下步的控制指令。代价计算[13]及专家决策是整个流程的核心环节,是本文航迹优化的主要研究问题。
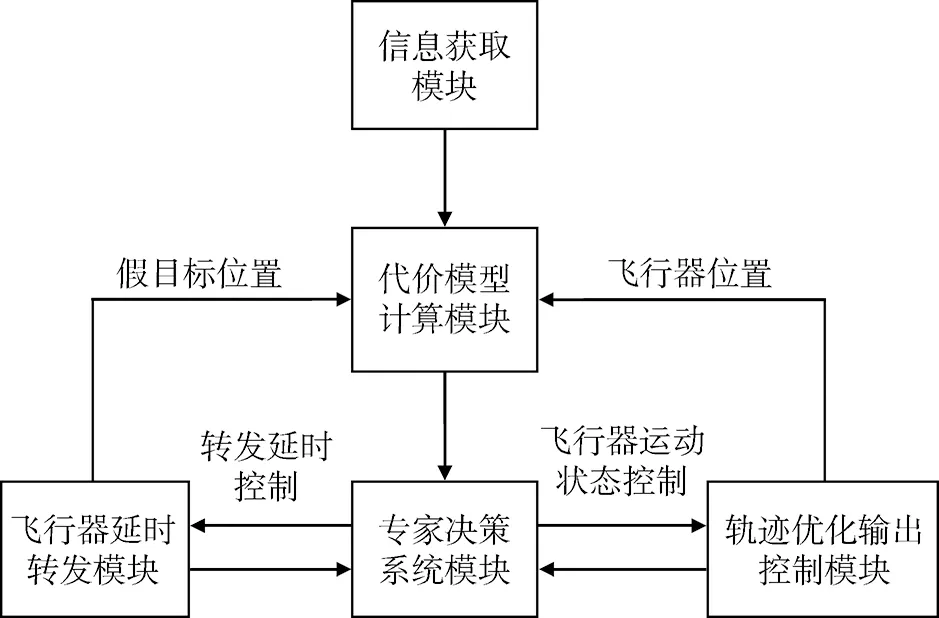
图2 协同干扰的流程Fig.2 Process of cooperative deception jamming
1.2 数学模型分析
单个干扰机对单部雷达形成的延时干扰航迹进行分析,如图3所示,将在二维平面对问题进行阐述。整个干扰过程的完成基于视线准则(line-of-sight, LOS),需要飞行器的速度、方位角及俯仰角及延时转发时间在空间中共同配合形成合理的假目标。
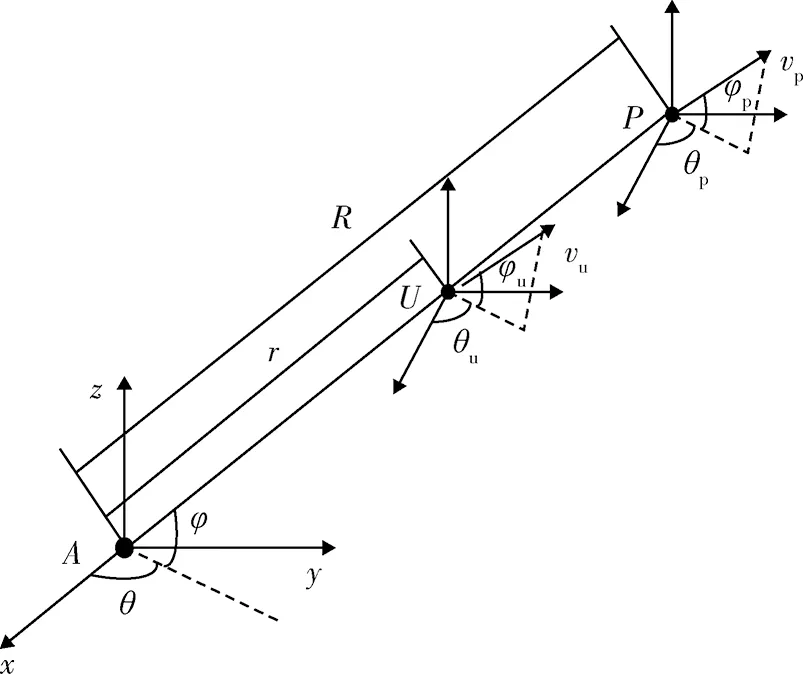
图3 干扰机及假目标轨迹间的运动关系Fig.3 Relationship of UAVs and phantom track
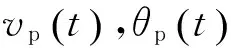
(1)
(2)
(3)
(4)
(5)
(6)
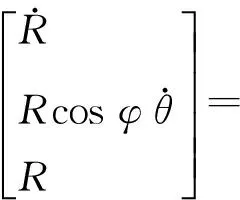
(7)
则由式(1),(2),(3),(7)最终可得
(8)
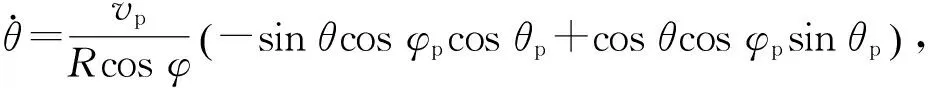
(9)
(10)
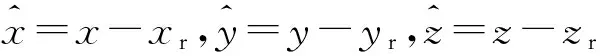
(11)
(12)

(13)
(14)

(15)
式中:α(t)为距离系数,是飞行器与假航迹到雷达距离的比值,0≤α(t)≤1,则
(16)
从式(16)中可以看出,整个系统的定位由vp,θp,φp及α共同决定的优化航迹。如何合理地规划假航迹的运行轨迹及距离系数的选取对于整个干扰系统的干扰效率起着至关重要的作用。
2 航迹优化问题分析
由第1节的分析可得,本文航迹优化问题可以转化为假目标航迹的及运动干扰机航迹的共同航迹规划问题。针对已有文献优化函数笼统、优化局限于运动特征的不足,对假目标航迹进行基于最小可识别概率的优化,对干扰机航迹进行基于最小推动力的优化。
2.1 假目标运动航迹规划
经过延时的干扰假目标会由于控制误差的出现,导致理想干扰点与实际位置出现一定的偏差。雷达网在不同位置的探测精度不同,因此在假航迹规划时,可根据雷达网探测精度的弱点,进行相应的延时转发。
设雷达网由N部雷达组成,第i部雷达部署的位置(xr(i),yr(i),zr(i)),各部雷达同时对假目标进行测量,得到测量值分别为(R(i),θ(i),φ(i)),其中R(i),θ(i),φ(i)为目标的距离、方位角、俯仰角信息,其对应的测量精度为σr(i),σθ(i),σφ(i)。假目标在三维坐标中的位置P为(x,y,z),根据极大似然估计可得P点定位精度的极限[14]为
(17)
(18)
式中各参数如下:
(19)
(20)
(21)
式中:R(i)为目标到第i雷达的距离;Rxy(i)是R(i)在Axy平面内的投影。
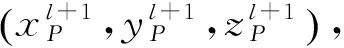
maxJP=GDOP(xP(l+1),yP(l+1),zP(l+1)),
(22)
且满足限制条件:
vmin≤vP≤vmax,
(23)
Δθmin≤uP2≤Δθmax,
(24)
Δφmin≤uP3≤Δφmax.
(25)
2.2 飞行器运动航迹规划
多干扰机在干扰过程中需要共同配合,以此达到多个假目标在空间中融合为同一目标的目的。因此,将距离系数α(t)作为优化干扰机运动模型的变量可以使优化模型更加合理。


图4 理想假目标与实际假目标位置误差示意Fig.4 Positional error of ideal and real false target
则由空间关系,可求得误差距离为
(26)
由式(26)可得,距离系数α越大,相对的融合误差越小,干扰成功概率越高。然而由于小型干扰飞机的速度与假目标所代表的突防飞机速度有较大差距,因此α应该在速度限制的范围内选取稍大的合理数值。
实际飞行过程中,飞机完成整个运动过程的难易度由飞机的推力决定,因此将飞行过程中的推力大小作为优化变量可以将干扰的难度降低。飞机飞行过程中推力有[15]:
(27)
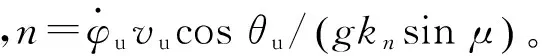
因此干扰机的优化问题转化为
(28)
且满足条件:
vmin≤vu≤vmax,amin≤au≤amax,
(29)
Δθmin≤θu≤Δθmax,
(30)
Δφmin≤φu≤Δφmax.
(31)
3 仿真分析
仿真实验1:假目标航迹的规划
仿真实验模拟3架干扰飞机对3部雷达进行干扰,雷达的具体参数如表1所示。
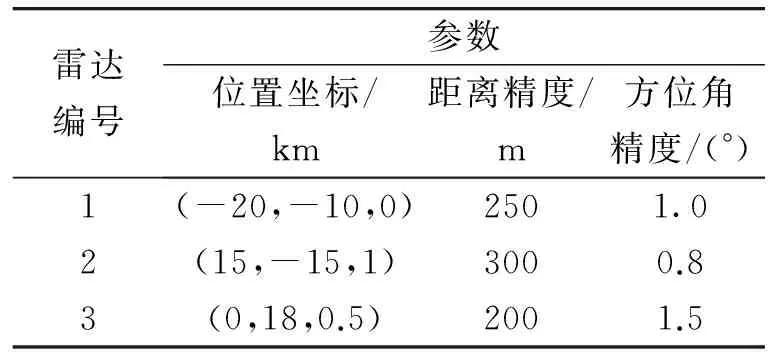
表1 雷达的具体参数Table 1 Radar parameters
由于假目标的飞行状态是否稳定决定着飞行器的运动状态,因此在实际干扰过程中应尽量保证假目标飞行状态趋于稳定,设置2组假目标的起始坐标分别为(-20,-5,8)及(-20,22,8),即分别从雷达网内部和外部飞行,假目标的速度为400 m/s,飞行高度保持在8 km,最大方位角速度1.5°/s,利用式(22)的优化条件进行优化,仿真结果如图5所示。
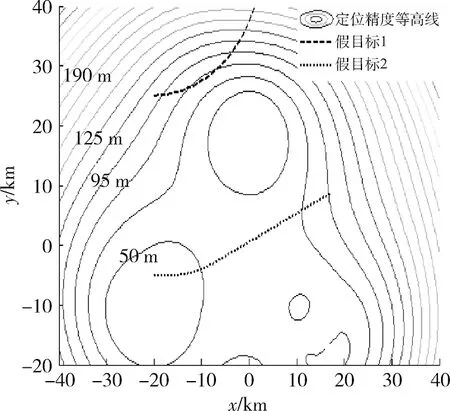
图5 雷达网定位精度及假目标航迹Fig.5 Position accuracy of radar networak and phantom track
从图5可以看出,假目标在雷达网内部穿越,沿雷达网定位精度变差的方向飞行,假目标飞行过程角度变化平稳,达到预期目的。
仿真实验2:飞行器航迹的规划
在仿真一基础上,对干扰机航迹进行规划。干扰机速度为150~250 m/s,最大加速度amax=6 m/s2,最大角方位速度θmax=8°/s,最大推力Fmax=3 500 N,W=145 kg,S=2 m2,g=9.81 kg/m2,ρ=1.225 kg/m3,CD0=0.02,k=0.1,kn=1,不考虑控制误差,初始距离系数设置为0.5,利用式(28)进行优化,对假目标1进行仿真结果如下。
图6~8给出了图5中假目标1条件下的干扰航迹及干扰机速度、 推力分析图, 从图中可看出,
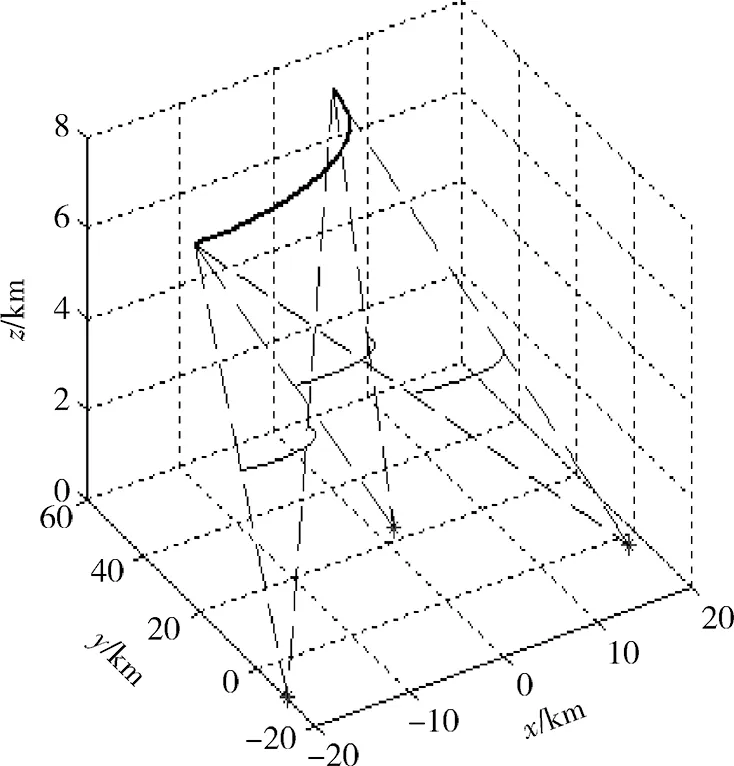
图6 干扰机及假目标运行轨迹Fig.6 Moving trajectory of UAVs and false target
飞行器在整个干扰过程运行平稳,速度、方位及俯仰角速度均能在限制范围运行,且干扰机推力随着时间推移逐步减小,可以完成干扰任务。
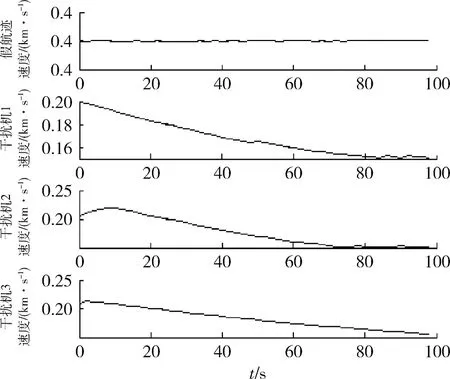
图7 干扰机及假目标速度分析Fig.7 Analysis of UAVs and false target

图8 假目标1对应干扰机飞行过程推力分析Fig.8 Thrust analysis of UAVs on condition 1
图9给出了干扰机随时间变化距离系数的变化,距离系数随时间推移而减小,因为在假航迹保持一定的情况下,距离系数的减小而导致干扰机速度变小,从而使优化变量推力变小,因此整个过程的运行是合理的。
图10给出了假目标2情况下飞行过程推力分析,与图7假目标1进行对比可看出,在本文条件下,在雷达网外部飞行推力更加稳定,可以更加顺利的完成干扰任务。

图9 干扰机距离系数分析Fig.9 Distance constant of UAVs

图10 假目标2情况下飞行过程推力变化Fig.10 Thrust analysis of UAVs on condition 2
仿真实验3:干扰成功率分析
由于飞行器控制误差的出现会导致假目标的理想方位与实际情况出现偏差,在仿真中,假设3部雷达同时对所侦察到的假目标进行跟踪,若3部雷达观测的假目标均在理想位置点处雷达网定位精度范围之内,则认为该假目标存在,否则认为该目标为假目标而排除。雷达的采样频率设为0.5 Hz,干扰机的位置距离误差为75 m,服从标准正态分布,分别对仿真1的2组假航迹仿真,干扰机的运行轨迹与仿真2相同,进行2 000次蒙特卡罗仿真。
仿真结果显示,假目标1情况下航迹点融合成功的概率为97.55%,假目标2情况下融合成功的概率为42.56%。可以看出,从雷达网外部进行干扰可以以更加可靠的融合概率完成干扰任务。
4 结束语
多飞行器协同干扰是对组网雷达进行航迹欺骗的有效手段,合理的运动状态规划可以将假航迹融合成功概率提高,同时将干扰机运动规划更加合理。本文针对前人进行航迹规划函数单一、规划效果不佳的问题,提出了高成功融合概率及低推力的代价函数,仿真实验表明,所提方法在雷达网外部飞行时优化效果理想,可操作性较高。本文对于研究组网雷达的航迹欺骗干扰提供了参考,但由于篇幅限制,初始距离系数的选取对于干扰效果的影响并未加以分析,将成为下一个研究的问题。
[1] 张锡祥. 现代雷达对抗技术[M].北京:国防工业出版社, 1998. ZHANG Xi-xiang. Modern Radar Counter Technology[M].Beijing: National Defence Industry Press, 1998.
[2] 杨涛. 组网雷达系统“四抗”效能评估方法研究[D]. 长沙:国防科学技术大学, 2008. YANG Tao. Study on Evaluation Method of “Four Countering” Efficiencies of Networked Radars[D].Changsha: National University of Defense Technology, 2008.
[3] 陆文博, 刘春生, 周青松. 基于SDP松弛的干扰资源优化分配技术研究[J]. 现代防御技术, 2014,42(6):167-172. LU Wen-bo, LIU Chun-sheng, ZHOU Qing-song. Jamming Resources Distribution Optimization Technology Based on SDP Relaxation[J]. Modern Defence Technology, 2014,42(6):167-172.
[4] BAR-SHALOM Y, LI X R. Estimation and Tracking: Principles, Techniques, and Software[M]. Norwood, MA: Artech House, 1993.
[5] BAR-SHALOM Y, LI X R, KIRUBARAJAN T. Estimation with Applications to Tracking and Navigation: Theory Algoriths and Software[M].New Jersey: John Wiley and Sons, 2001.
[6] MCCLAIN T W, CHANDLER P R, PACHTER M. A Decomposition Strategy for Optimal Coordination [C]∥ Unmanned Air Vehicles. Proc. Of the Acc, 2000.
[7] Keith B Purvis, Karl J Astrom, Mustafa Khammash. Estimating Radar Positions Using Cooperative Unmanned Air Vehicle Teams[C]∥2005 American Control Conference, 2005,6:3512-3517.
[8] Keith B Purvis, Phillip R Chandler. A Review of Recent Algorithms and a New and Improved Cooperative Control Design for Generating a Phantom Track[C]∥2007 American Control Conference, 2007,7:3252-3258.
[9] Scott D Waun, Umit Ozguner. Deception of Radar System using Cooperatively Controlled Unmanmed Air Vehicles[C]∥ 43rd IEEE Conference on Decision and Control,2004,12:3370-3375.
[10] Mark J Mears, Maruthi R Akella. Proceedings of the 2005 Networking[C]∥ Sensing and Control, 2005, 3:332-335.
[11] 党立坤, 王小念, 张建科, 等. 基于DRFM的欺骗干扰及反干扰[J]. 舰船电子对抗, 2010, 33(2):23-26. DANG Li-kun, WANG Xiao-nian, ZHANG Jian-ke, et al. Deceptive Jamming and Anti-Jamming Based on DRFM[J]. Shipboard Electronic Counter Measure, 2010, 33(2):23-26.
[12] 吴永刚. 基于DRFM的有源雷达干扰技术研究[D].长春:吉林大学, 2013. WU Yong-gang. Study on Active Radar Jamming Technology Based on DRFM[D].Changchun: Jilin University, 2013.
[13] 王威, 许鹏, 张多林. 混合优化策略在巡航导弹多航迹规划中的应用[J]. 电光与控制,2008, 15(4):66-69. WANG Wei, XU Peng, ZHANG Duo-lin. Application of Mixed Optimized Strategy in the Multiple Route Planning for A Cruise Missile[J]. Electronic Optics & Control, 2008, 15(4):66-69.
[14] 赵志超. 导弹防御雷达网数据融合技术研究[D].长沙:国防科学技术大学, 2010. ZHAO Zhi-chao. Study on Data Fusion Techniques of Missile Defense Radar Network[D].Changsha: National University of Defense Technology, 2010.
[15] XU Yun-jun,GARETH Basset. Optimal Coherent Phantom Track Design Using Virtual Motion Camouflage[C]∥2010 American Control Conference, 2010, 6:5400-5405.
Strategy for Track Deception Jamming Against Radar Network Using Cooperative Autonomous Vehicle Teams
LI Xiao-bo, SUN Lin, ZHOU Qing-song, SHAN Liang
(Elctronic Engineering Institute,Anhui Heifei 230037,China)
For the characteristics of radar network which has strong antijamming capacity, the feasibility of cooperative deception jamming against radar network is analyzed by using a team of unmanned aerial vehicles (UAVs). Firstly, the motional condition of completing the deception Jamming is discussed by analyzing geometrical relationship, then a step-by-step mathematical model is proposed to optimize the phantom track. This model can reduce the difficulty of cooperative jamming, make phantom target keep away from threatening area and move toward destination. The simulated results prove the feasibility of the model.
cooperative unmanned aerial vehicles(UAVs) cooperative; deception jamming; radar network; path optimization; digital radio frequency memory(DRFM); minimum thrust
2016-01-18;
2016-03-11
安徽省科技攻关项目(1310115188)
李小波(1970-),男,四川仁寿人。副教授,博士,主要研究方向为雷达及雷达对抗理论。
10.3969/j.issn.1009-086x.2016.06.008
TN972+.3
A
1009-086X(2016)-06-0043-07
通信地址:230037 安徽省合肥市蜀山区黄山路460号502室
E-mail:lxb_eei@163.com
