基于灰色聚类理论的非合作目标交会效能评估*
2016-02-24化金朱学昌王立旭
化金,朱学昌,王立旭
(北京宇航系统工程研究所,北京 100076)
空天防御体系与武器
基于灰色聚类理论的非合作目标交会效能评估*
化金,朱学昌,王立旭
(北京宇航系统工程研究所,北京 100076)
由于空间非合作目标航天器的特性不完全已知,将空间非合作目标视为灰色系统,利用灰色聚类理论评估交会效能。选择跟踪精度、预报精度、交会精度和交会窗口为评估指标,使用熵权法确定指标权重。考虑目标航天器变轨时刻和变轨加速度不同情况,分别仿真计算指标观测值,评估交会效能。仿真算例评估结果说明效能评估方法具有客观性和有效性。
航天系统工程;效能评估;灰色聚类;非合作目标;评估指标;信息熵
0 引言
空间非合作目标泛指不能提供有效合作信息的空间目标[1],包括故障或失效卫星、空间碎片、废旧航天器等。非合作目标交会技术是航天器在轨服务、空间垃圾清除[2]、空间对抗等热门领域的关键技术[3]。与合作目标交会问题不同的是,非合作目标本身没有配备目标识别器和交会敏感器[4],而且姿态、轨道不受控制,出现自由翻滚、轨道下降的现象。
非合作目标的物理特性和运动特性是不完全已知的,属于不确定性系统。概率统计、模糊数学、灰色系统理论和粗糙集理论是4种最常用的不确定性系统研究方法[5]。与概率统计研究“随机不确定”对象、模糊数学解决“认知不确定”问题、粗糙集理论处理“边界不清晰”情况不同,灰色系统理论以“部分信息已知,部分信息未知”的不确定性系统为研究对象,通过挖掘“部分”已知信息,提取有用信息,实现系统认知的目的。
空间非合作目标交会问题中包含了相对位姿测量、交会导航制导控制、抓捕与对接机构设计等关键技术,并需要多类传感器和航天器组成系统实现交会任务。以往的研究中常以测量精度、导航精度、控制精度等单一指标评价交会问题的研究成果[6-8],然而对交会系统在规定条件、规定时间内完成规定任务的程度[9],即系统效能应该采用综合指标进行评估。目前针对空间非合作目标交会效能评估方法的研究较少,本文利用灰色聚类理论,设计评估指标,建立空间非合作目标交会效能评估方法,并通过仿真算例说明评估方法的客观性和有效性。
1 效能评估指标设计
空间非合作目标交会过程中,被动交会航天器称为目标航天器,主动交会航天器称为追踪航天器。追踪航天器在飞行的初始阶段,距离目标航天器很远,地基或者天基的测量控制系统搜索、跟踪目标航天器轨迹,预报未来轨道,形成导航信息,向追踪航天器发送制导指令,这个阶段称为远距离导引段。当追踪航天器上的交会敏感器捕获目标航天器后,进入自主寻的段,控制系统导引追踪航天器到达目标航天器附近某一点。最后根据具体的交会任务,追踪航天器张开捕获网或机械臂捕捉非合作目标,或者对目标进行伴飞、绕飞,或者以一定的相对姿态与目标对接。
测控系统的目标跟踪、轨道预报和追踪航天器的自主寻的、变轨交会都是空间非合作目标交会的重要环节。跟踪精度、预报精度和交会精度影响交会任务的完成效果,所以应成为评估空间非合作目标交会的综合效能指标。此外,由于非合作目标的特征不完全确定,交会窗口的长度会影响追踪航天器应对目标航天器突发状况的效果,因此也应成为评估指标之一。因此,交会效能评估指标包括:跟踪精度、预报精度、交会精度和交会窗口。
2 评估指标计算模型
本文建立空间非合作目标交会仿真系统,通过仿真计算的方法获取评估指标的数值。仿真系统包括目标航天器运动模型、目标跟踪模型、轨道预报模型和追踪航天器交会模型。
(1)目标航天器运动模型
在地心惯性坐标系下建立目标航天器的运动方程
(1)
式中:r=(x,y,z)为地心惯性坐标系下的位置矢量;v=(vx,vy,vz)为地心惯性坐标系下的速度矢量;a=(ax,ay,az)为地心惯性坐标系下的航天器推力加速度矢量;μ为地心引力常数;用下标tar代表目标航天器。
对于测控系统和追踪航天器,已知目标航天器具有一定的变轨能力,但是未知目标变轨时刻、变轨加速度大小和形式。假设目标采取单脉冲变轨,变轨时刻为t1,变轨加速度为常值‖atar‖=aj,方向为轨道面的法线方向,变轨持续时间t。
(2) 目标跟踪模型
假设测控系统、航天器上敏感器测量3个参数:目标与追踪航天器的相对距离、视线俯仰角和视线方位角,利用扩展卡尔曼滤波算法(EKF)[10]估计目标的运动状态X=(rtar,vtar,atar),进行目标航天器轨迹跟踪。跟踪算法为
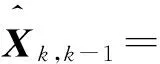
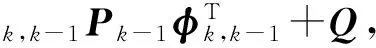
(2)
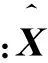
(3) 轨道预报模型
本文采用输入为白噪声的一阶时间相关模型(Singer模型)[11]描述非合作目标的变轨加速度为
(3)
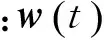
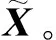
(4) 追踪航天器交会模型
将目标航天器轨道坐标系选为追踪航天器与目标航天器的相对运动参考坐标系,相对位置矢量为rrel=(x,y,z),参考坐标系相对于地心惯性坐标系的角速度为目标航天器轨道角速度ω,则相对运动方程[8]为
(4)
式中:ax,ay,az为轨道坐标系下的加速度分量,下标cha代表追踪航天器。
追踪航天器在测控系统导引下飞向预设交会点,探测到目标变轨后,按照变轨策略在推力的作用下实施变轨,飞向新的交会点。交会过程如图1所示,在交会时刻目标航天器与追踪航天器的相对距离为交会误差。当追踪航天器采取不同的变轨策略,可在不同交会时刻以较小的误差交会。将满足交会误差上限要求的交会时刻组成的时段定义为交会窗口Tj,追踪航天器可在窗口内完成捕捉、对接或者伴飞等任务。每类任务对于交会误差上限的要求不同,文本仿真计算时取5 m。在交会窗口内,交会误差的平均值定义为交会精度δj=‖rrel‖。

图1 空间非合作目标交会过程示意图Fig.1 Sketch map of process of rendezvous with space noncooperative target
3 灰色聚类评估方法
灰色聚类评估主要用于“少数据”“贫信息”情况下的多指标系统评估[12],设定若干个灰类,以反映评估对象不同的等级,如“优”、“良”、“中”、“差”。根据聚类对象不同,灰色聚类评估分为灰色关联聚类评估和基于白化权函数的灰色聚类评估2类[13]。根据权重的不同,基于白化权函数的灰色聚类又分为灰色变权聚类和灰色定权聚类[14]。灰色关联聚类评估主要用于归并同类因素、简化系统、减少不必要数据的收集。基于白化权函数的灰色聚类评估主要用于考察观测对象属于事先设定的某个类别。灰色变权聚类适用于指标意义、量纲皆相同的情形,而灰色定权聚类适用于指标意义或者量纲不同的情况。由于空间非合作目标交会问题物理意义明确,不需要简化系统、合并同类项,评估指标意义、量纲不同,且在数量上差异较大,因此文本采用基于白化权函数的灰色定权聚类方法[14]。聚类评估方法具体步骤如下:
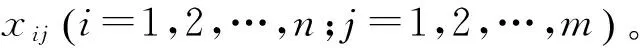
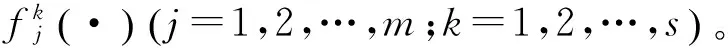
(5)
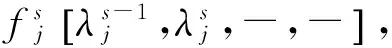
(6)
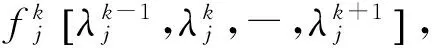
(7)
(8)
指标j的熵权为
(9)
第4步:根据指标权重和观测值,计算灰色定权聚类系数
(10)
4 交会效能评估算例
4.1 算例仿真场景设定
设定非合作目标航天器分别按照表1中6种变轨参数飞行,以aj为标准,编号1,2可以看作目标“弱变轨”,而3~6为“强变轨”;以t为标准,编号1~4为“长时间”,而5,6为“短时间”;以t1为标准,编号1,3,5为“早变轨”,而2,4,6为“晚变轨”。通过上述3个参数的排列组合,可将目标变轨飞行分为6种与之对应的情况,并将这6种情况作为交会效能评估对象。以编号1的目标航天器变轨时刻为时间原点,从1 250~1 350 s每间隔5 s作为一个交会时刻,对追踪航天器与目标交会的过程进行仿真。
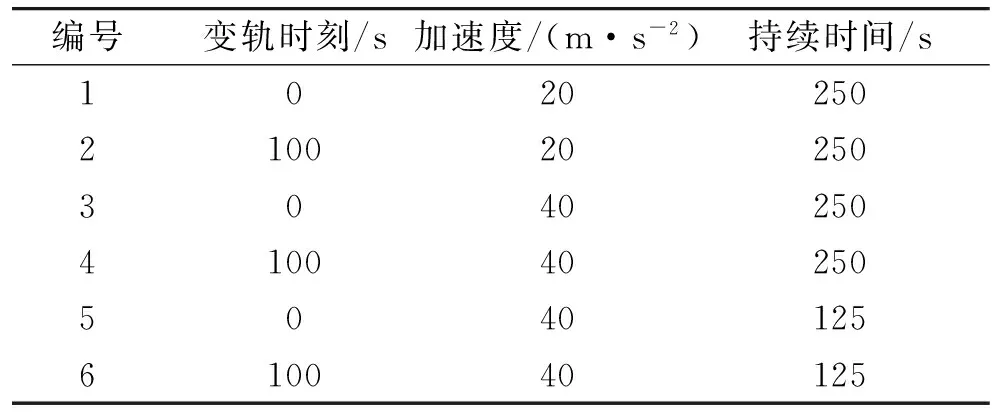
表1 目标航天器变轨参数Table 1 Orbit transfer parameters of target spacecraft
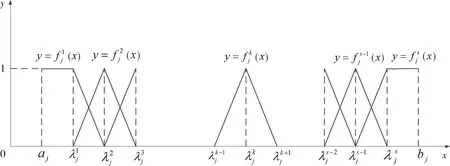
图2 中心点混合三角白化权函数示意图Fig.2 Sketch map of mixed triangular whitenization weight function
4.2 效能评估
在21个交会时刻中,追踪航天器对目标(编号1)的交会误差如图3所示。除1 250 s的交会误差大于上限5 m以外,1 255~1 350 s的交会误差均满足要求,所以交会窗口为95 s。1 255~1 350 s的交会误差平均值(交会精度)为1.89 m、跟踪精度为21.90 m、预报精度为40 383 m。通过仿真计算,6个评估对象对4个交会评估指标:跟踪精度、预报精度、交会精度和交会窗口(分别对应j=1,2,3,4)的指标值如表2所示。

表2 效能评估指标值Table 2 Value of effectiveness evaluation index
从表2看出,在非合作目标交会的过程中,轨道预报精度远远低于目标跟踪精度,相差3个量级。这是由于目标跟踪时测控系统与交会敏感器的测量数据输入到滤波算法中,将估计误差维持在很小的范围内波动,因此目标跟踪的精度比较高。而轨道预报仅通过积分运动微分方程组得到估计值,初始值的误差随着时间逐渐累积到很大的数值。在仿真设置的变轨参数中,无论目标航天器进行早/晚、强/弱、长/短时间的变轨飞行,追踪航天器都能在某时长的交会窗口内,以小于5 m的交会精度与目标航天器交会。
本文将4个指标分为 “优”、“良”、“中”、“差”(分别对应k=1,2,3,4)这4个灰类。对于前3个指标,误差越小,精度越高,越有利于交会,权函数的转折点从小到大排列。而对于交会窗口,时间越长,越有利于交会任务的完成,因此转折点从大到小排列。结合经验值,选取三角白化权函数的转折点与中心点分别为
b3=5,
将观测值进行归一化处理,计算指标的熵权为
ω1=0.055 4,ω2=0.506 7,ω3=0.034 3,ω4=0.403 7.
从指标熵权来看,跟踪精度和交会精度的变化很小,这2个指标的权重也小,总和接近0.1。交会窗口变化较大,预报精度变化最大,这2个指标的权重也大。说明了熵权法通过观测值信息差异的大小决定指标的权重,并通过聚类系数反映到了评估结果中。相比利用专家打分等形式确定的指标权重,熵权法具有客观性和可信性。4个指标观测值的意义、量纲不同、数量上差距很大,相比灰色变权聚类方法,采用灰色定权聚类方法,可以充分发挥每个指标在聚类评估中的作用。

图3 每个交会时刻的交会误差Fig.3 Rendezvous error at each rendezvous time
计算灰色定权聚类系数,i=1时
0.403 7.
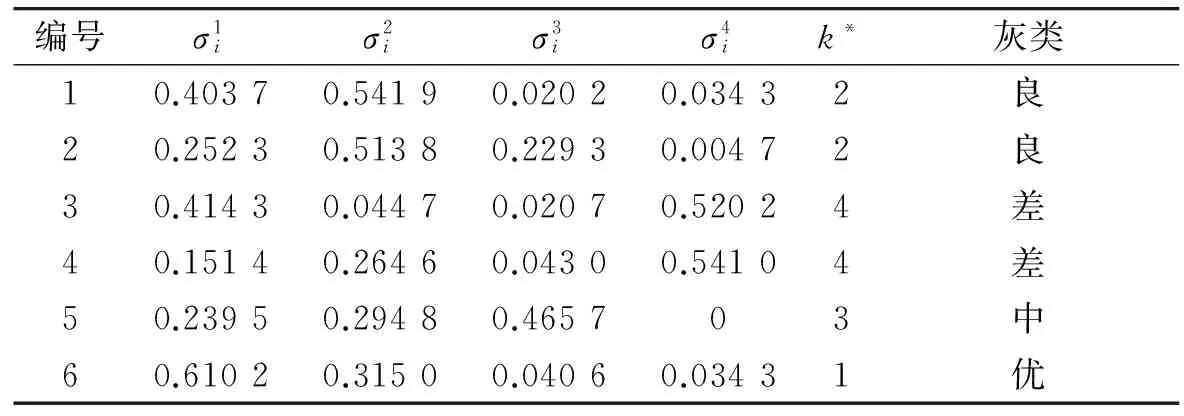
表3 聚类系数与评估结果Table 3 Clustering coefficient & evaluation result
4.3 评估结果分析
从表3看出,交会效能“优”的情况为编号6,“良”的情况为编号1和2,“中”的情况为编号5,“差”的情况为编号3和4。针对非合作目标航天器的不同变轨情况,无论变轨早晚,对于“长时间”、“强变轨”的目标航天器(编号3和4),交会的评估结果是最差的。对于“长时间”、“弱变轨”的目标(编号1和2),评估交会的结果是“良”,这是由于目标变轨前后轨道差异小于“强变轨”的情况,追踪航天器与此类目标交会更加容易。对于“短时间”、“强变轨”的目标(编号5和6),因为目标变轨时间短,测控系统预报误差累积小,对交会误差影响小。尤其是当目标“晚变轨”时,预报精度最高、交会窗口较长,导致交会效果较好,评价结果为“优”。但是当目标“早变轨”时,交会窗口变短,导致交会效果下降,评价结果为“中”。
综合以上分析,效能评估的结果科学有效。相比选择单一指标进行效能评估的方法,本文研究的方法更加客观全面。
5 结束语
本文基于灰色聚类理论建立了空间非合作目标交会的效能评估方法。根据空间非合作目标交会的过程,选择跟踪精度、预报精度、交会精度和交会窗口为评估指标。在仿真系统中建立目标航天器运动模型、目标跟踪模型、轨道预报模型和追踪航天器交会模型。通过仿真算例说明了效能评估方法的客观性和有效性。
[1] Committee on the Assessment of Options for Extending the Life of the Hubble Space Telescope, National Research Council. Assessment of Options for Extending the Life of the Hubble Space Telescope: Final Report[M]. Washington, WA, USA: National Academies Press, 2005.
[2] LEONOR M, BRUNO C. Covariance Analysis Tool for Far Non-Cooperative Rendezvous [C]∥AIAA Guidance, Navigation, and Control Conference, Boston, USA, August 19-22, 2013.
[3] 马宝林,桂先洲. 空间非合作目标形式概念分析[J]. 吉首大学学报:自然科学版,2012,33(4):87-90. MA Bao-lin, GUI Xian-zhou. Analysis of Formal Concept of the Space Non-Cooperative Target [J]. Journal of Jishou University:Natural Science ed, 2012,33(4): 87-90.
[4] 刘涛,解永春. 非合作目标交会相对导航方法研究[J]. 航天控制,2006,24(2):48-53. LIU Tao, XIE Yong-chun. A Study on Relative Navigation for Spacecraft Rendezvous with a Non-Cooperative Target [J]. Aerospace Control, 2006, 24(2):48-53.
[5] 刘思峰,杨英杰,吴利丰. 灰色系统理论及其应用[M]. 北京:科学出版社,2014:113-115. LIU Si-feng, YANG Ying-jie, WU Li-feng. Grey System Theory and Application [M]. Beijing: Science Press, 2014: 113-115.
[6] XU Wen-fu, LIANG Bin, LI Cheng, et al. Autonomous Rendezvous and Robotic Capturing of Noncooperative Target in Space [J]. Robotica, 2010, 28(3): 705-718.
[7] 张立佳. 空间非合作目标飞行器在轨交会控制研究[D]. 哈尔滨:哈尔滨工业大学,2008. ZHANG Li-jia. Research on Control for Rendezvous with Noncooperative Target in Orbit [D]. Harbin: Harbin Institute of Technology, 2008.
[8] 陈密密. 用于空间非合作目标交会的相对测量算法研究[D]. 郑州:解放军信息工程大学,2009. CHEN Mi-mi. Research on Relative Measurement Algorithm of Space Rendezvous with A Noncooperative Target [D]. Zhengzhou: PLA Information Engineering University, 2009.
[9] 张杰. 效能评估方法研究[M].北京:国防工业出版社, 2009. ZHANG Jie. Study on Effectiveness Evaluation Theory [M]. Beijing: National Defense Industry Press, 2009.
[10] 秦永元. 卡尔曼滤波与组合导航原理[M]. 西安:西北工业大学出版社,2012:51-52. QIN Yong-yuan. Kalman Filter and Integrated Navigation Theory [M]. Xi’an: Northwestern Polytechnical University Press, 2012:51-52.
[11] 潘泉. 现代目标跟踪与信息融合[M]. 北京:国防工业出版社,2009. PAN Quan. Modern Target Tracking and Information Fusion [M]. Beijing: National Defense Industry Press, 2009.
[12] 余静,张勇涛,张松良. 基于灰色聚类理论的C4ISR系统效能评估研究[J]. 现代防御技术,2009,37(3):64-67. YU Jing, ZHANG Yong-tao, ZHANG Song-liang. Evaluation Method of C4ISR System Effectiveness Based on Grey Cluster Theory [J]. Modern Defense Technology, 2009, 37(3):64-67.
[13] ZHANG Ke, LIU Si-feng. Research on Extended Cluster of Grey Incidence and Its Application [C]∥2009 IEEE International Conference on Grey Systems and Intelligent Services, Nanjing, China,November 10-12, 2009.
[14] 王正新,党耀国,刘思峰. 基于白化权函数分类区分度的变权灰色聚类[J]. 统计与信息论坛,2011,26(6): 23-27. WANG Zheng-xin, DANG Yao-guo, LIU Si-feng. Grey Clusters with Variable Weights Based on the Classification Degree of the Whitening Weight Functions [J]. Statistics & Information Forum, 2011, 16(6):23-27.
[15] 米传民,刘思峰,党耀国,等. 灰色熵权聚类决策方法研究[J]. 系统工程与电子技术,2006,28(12):1823-1825. MI Chuan-min, LIU Si-feng, DANG Yao-guo, et al. Study on Grey Entropy Weight Clustering Decision-Making [J]. Systems Engineering and Electronics,2006,28(12):1823-1825.
Effectiveness Evaluation of Rendezvous with Space Non-Cooperative Target Based on Grey Clustering Theory
HUA Jin,ZHU Xue-chang, WANG Li-xu
(Beijing Institute of Aerospace Systems Engineering, Beijing 100076,China)
Due to the uncertainty of space non-cooperative target, the target is regarded as a grey system, and the effectiveness evaluation of rendezvous is based on grey clustering theory. Tracking precision, predicting precision, rendezvous precision and rendezvous window are chosen as indicators, and their weights are decided by entropy. Considering different orbit transfer time and acceleration, the data of indicators are calculated respectively by simulation, and the effectiveness of rendezvous is evaluated with thegrey cluster method. Simulation result shows that effectiveness evaluation method is of objectivity and credibility.
aerospace systems engineering; effectiveness evaluation; grey clustering; non-cooperative target; evaluation index; entropy
2015-11-19;
2016-02-16
化金(1991-),女,北京人。硕士生,主要研究方向为飞行器设计研究。
10.3969/j.issn.1009-086x.2016.06.003
V57;TP301.6
A
1009-086X(2016)-06-0013-06
通信地址:100076 北京9200信箱10分箱10号
E-mail:huajin112358@163.com
