后缘连续变弯度对跨声速翼型气动特性的影响
2016-02-24郭同彪白俊强杨体浩西北工业大学航空学院西安710072
郭同彪, 白俊强, 杨体浩 西北工业大学 航空学院, 西安 710072
后缘连续变弯度对跨声速翼型气动特性的影响
郭同彪, 白俊强*, 杨体浩 西北工业大学 航空学院, 西安 710072
针对后缘连续变弯度对跨声速翼型气动特性的影响进行了研究。首先不考虑翼型后缘连续变弯度,基于搭建的优化设计系统对跨声速翼型进行气动减阻优化设计,通过添加不同的约束优化得到两种跨声速翼型:无激波翼型和超临界翼型。然后在这两种翼型的基础上,以后缘偏转角度为设计变量、以阻力系数最小为目标,针对不同的升力系数分别进行优化设计,并根据优化结果深入分析后缘连续变弯度对这两种翼型极曲线特性的影响机理。优化结果表明:无激波翼型与超临界翼型相比,其设计点处的气动特性较好,但鲁棒性较差;升力系数小于设计升力系数时,应用后缘连续变弯度后,无激波翼型的极曲线特性明显提高,减阻最高达到3.9%,而超临界翼型的极曲线特性提高不明显;升力系数大于设计升力系数时,应用后缘连续变弯度后,无激波翼型和超临界翼型的极曲线特性都明显提高,减阻分别达到 2.4%~18.1% 和1.7%~13.2%。
后缘连续变弯度; 无激波翼型; 超临界翼型; 优化设计; 鲁棒性; 极曲线
近年来,波音公司和美国国家航空航天局(National Aeronautics and Space Administration, NASA)联合开展了“可连续变弯度后缘襟翼”的项目研究,目的在于提高未来运输机的飞行性能。其中一个主要的目标是通过连续改变后缘弯度,提高整个巡航阶段的升阻特性[1-2]。对于大型客机,阻力降低1%可使直接使用成本降低0.2%[3],而减小直接使用成本是提高民用飞机市场竞争力的有效手段。因此,后缘连续变弯度具有重大的研究意义。
1994年,密歇根大学Kota[4]教授首次提出了用柔性机构实现机翼前后缘变形的设计思想,利用柔性机构驱动器将能量传至机翼表面,实现机翼形状的改变。2003年,密歇根大学Kerr-Jia和Kota[5]以变后缘机翼为例阐述了形状变化柔性机构的设计方法。2008年,欧盟的FP7项目对变形后缘等高升力装置及其驱动机构进行了研究[6]。2014年,东京大学Yokozeki和Sugiura[7-8]研究了后缘采用瓦楞结构的变形机翼,实现了后缘光滑无缝变形,并且具有较强的变形能力;通过风洞试验对连续变弯度翼型和有缝变弯翼型的气动特性进行对比,指出连续变弯度翼型具有更好的升力特性。2014年,Kaul和Nguyen[9]通过将翼型后缘偏转指定角度研究后缘变弯度对翼型气动特性的影响。
在国内,西北工业大学杨智春等[10-11]对柔性后缘进行了不同偏转轨迹的方案设计和气动特性分析,并与带刚性后缘机翼的气动特性进行了比较。中国航天空气动力技术研究院陈钱等[12]以变弯度翼型为研究对象,对比分析了不同的连续光滑变形翼型与传统偏转翼型的气动特性, 讨论了变形参数对气动特性的影响。上海交通大学孔博等[13]研究了前缘和后缘连续变弯度对低速状态下增升的影响。西北工业大学黄杰[14]、赵飞[15]等对柔性机翼前缘和后缘进行了拓扑优化分析。南京航空航天大学王婷等[16]对可变机翼后缘的柔性机构进行了拓扑优化。哈尔滨工业大学尹维龙等[17]提出了一种可放大驱动力的索网传动机构,提高了变体后缘的驱动效率。南京航空航天大学刘卫东等[18]对基于超声电机驱动的后缘变弯度机翼进行了探索性研究,实现了由自主研制的超声电机驱动的小型变弯度机翼的系统集成,并通过风洞试验验证了方案的可行性。
从国内外的研究概况来看,大部分的研究内容都集中于柔性变弯度机翼的结构设计和拓扑优化方面,有关连续变弯度对翼型的气动特性影响的研究较少,且多数只针对低速和亚声速翼型。
本文致力于研究后缘连续变弯度对跨声速翼型气动特性的影响,探索应用后缘连续变弯度后的减阻机理。主要研究内容包括以下3个方面:①将一种翼型后缘连续变弯度系统[19]抽象简化,建立相应的力学模型,并以后缘偏转角度为设计变量实现后缘连续变弯度的参数化;②通过添加不同的约束,优化得到两种跨声速翼型,即无激波翼型和超临界翼型;③在优化得到的两种跨声速翼型的基础上,研究后缘连续变弯度对翼型极曲线特性的影响,并对影响机理进行深入分析。
1 翼型后缘连续变弯度的参数化
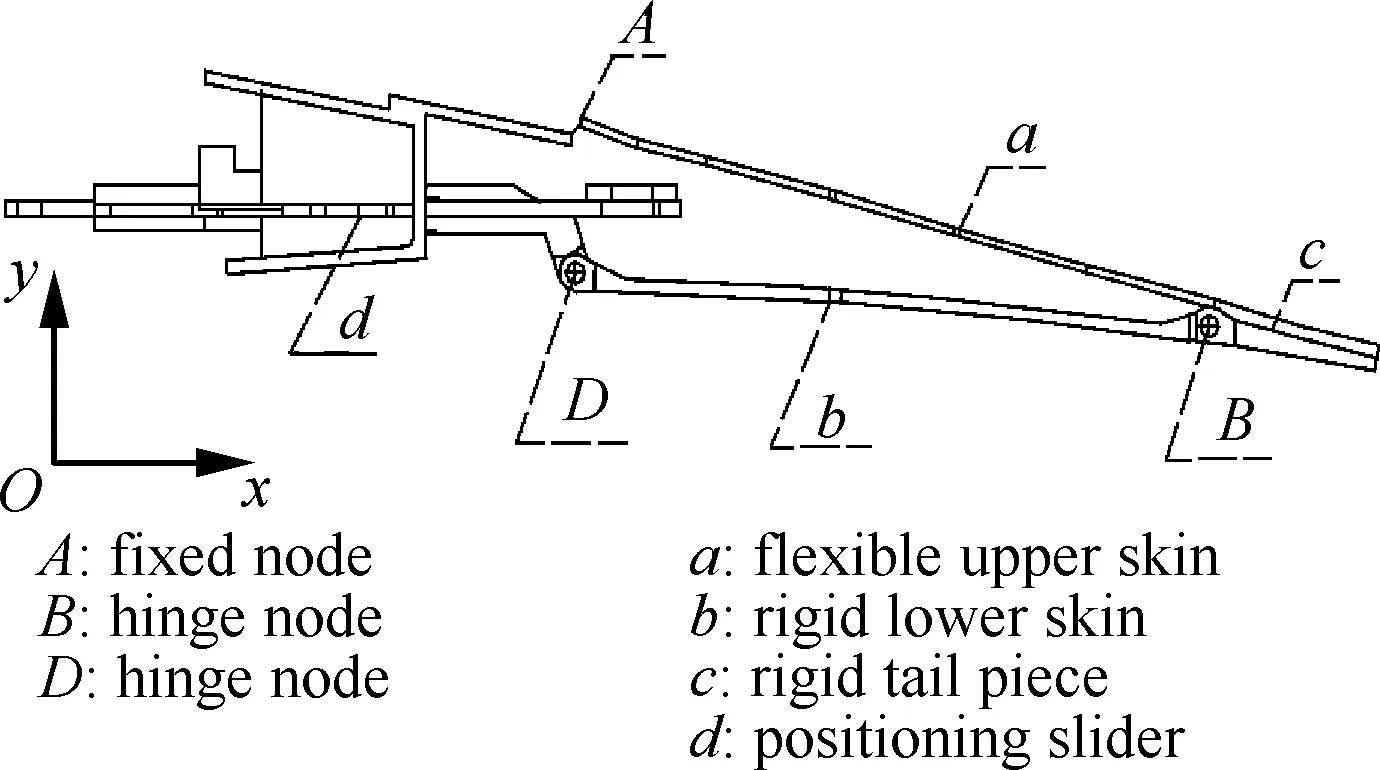
图1 后缘连续变弯度系统[19]
Fig.1 Continuous trailing-edge variable camber system[19]
波音公司申请了一个改变飞行器机翼后缘弯度的设备,如图1所示[19]。柔性上蒙皮(图1中“a”所示)在前边界附接到翼梁;刚性下蒙皮(图1中“b”所示)在刚性尾部件(图1中“c”所示)互连到柔性上蒙皮;至少一个致动连杆附接到刚性尾部件,并在刚性下蒙皮的前边界具有铰链(图1中“D”所示);至少一个定位滑动器(图1中“d”所示)附接到铰链。向后推动定位滑动器,铰链向后移动,并带动刚性下蒙皮向上旋转、柔性上蒙皮向上弯曲;向前推动定位滑动器铰链向前移动,并带动刚性下蒙皮向下旋转、柔性上蒙皮向下弯曲;从而实现机翼弯度的改变,而后缘能够改变的角度可以是上偏10°至下偏55°之间的任意一个值。
在本文中,将刚性下蒙皮等效为两端铰接的刚性运动曲梁,柔性上蒙皮等效为一端固支一端铰接的柔性曲梁模型。为了简化分析,忽略梁受到的气动力、重力等分布力,仅考虑作用在两端的集中力。此外,假设柔性曲梁的弯曲刚度沿轴向为常数且不考虑拉伸变形。图2为这两个梁的受力分析图(A、B和D的含义与图1中相同),由静力学定理可知:
(1)
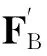
刚性运动曲梁端点在坐标系Oxy的坐标为
(2)
式中:θ为直线DB与x轴的夹角;xB、yB、xD和yD分别为刚性运动曲梁端点的坐标;L为连线BD的长度。
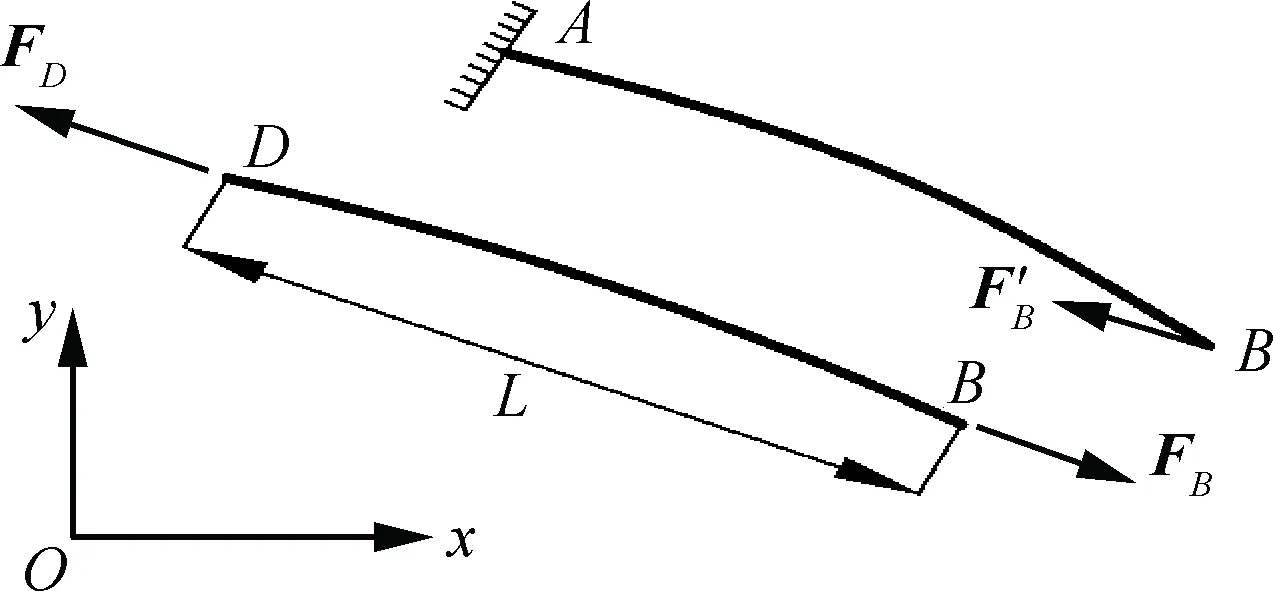
图2 后缘连续变弯度系统的简化模型
Fig.2 Simplified model of continuous trailing-edge variable camber system
以A点为坐标系原点,沿柔性曲梁建立自然坐标系s。在自然坐标系下,梁曲率与弯矩的关系为
(3)
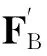
步骤1 给定θ角,可以得到FB的方向和yB的值。
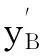
步骤3 根据x(s)、y(s)和FB求解M(s),代入式(3)得到K(s),进而积分得到x(s)和y(s)。
步骤4 重复步骤3,直到x(s)和y(s)收敛。
通过上述步骤实现了以后缘偏转角为设计变量的后缘变弯的参数化。
2 优化设计系统
建立的优化设计系统主要由参数化模块、网格自动生成模块、CFD(ComputationalFluidDynamics)计算模块和优化搜索模块组成,优化流程如图3所示。网格自动生成模块采用径向基函数插值动网格方法,根据新的翼型和初始网格得到每个新翼型的流场计算网格。在不考虑翼型后缘连续变弯度的气动减阻优化设计中,采用基于Bernstein基函数的EFFD(ExtendedFreeFormDeformation)参数化方法[20],EFFD参数化方法是对FFD(FreeFormDeformation)参数化方法的扩展,以非平行六面体作为控制体,可以更好地贴近变形物体,有效地提高控制点对物体局部细节的变形能力。在对后缘偏转角度进行优化设计时,以后缘偏转角度为设计变量,编程实现翼型后缘弯度的改变。遗传算法(GeneticAlgorithm,GA)借助生物进化过程中“适者生存”的规律,模仿生物进化过程中的遗传繁殖机制,对优化问题编码,然后对编码的个体进行选择、交叉和变异等操作,通过迭代从新种群中寻找最优解。本文采用具备精英策略的非支配排序遗传算法(Non-dominatedSortingGeneticAlgorithm-Ⅱ,NSGA-Ⅱ),该算法在优化的过程中不需要罚函数,而是将不满足约束的个体视为最差的。

图3 优化设计系统流程图
Fig.3 Flowchart of optimization design system
3 数值求解器验证
CFD计算模块对优化设计过程中的个体进行气动力评估计算。本文流场求解器求解RANS(ReynoldsAveragedNavier-Stokes)控制方程,采用隐式时间推进方法,空间离散为二阶Roe格式,全湍流计算,湍流模型为SST(ShearStressTransport)。利用多重网格和并行计算技术提高求解速度。用此求解器对RAE2822翼型的case9[21]进行气动特性评估,计算状态为:马赫数Ma=0.73,升力系数CL=0.8,雷诺数Re=6.5×106。采用本文方法计算的气动力系数与试验的气动力系数对比如表1所示,其中, CD为阻力系数,Cm为相对四分之一弦长点的力矩系数。从表1中可以看出,无论是阻力系数还是力矩系数,计算结果与试验值基本一致。计算的压力系数与试验的压力系数对比如图4所示,由图4可以看出,两者吻合得较好。综上可以看出,本文采用的流场求解器是可靠的。
表1 气动力系数试验值[21]与本文方法计算结果对比
Table 1 Comparison of aerodynamic coefficients between present method and experiment[21]

MethodCLCDCmExperiment0.8030.01680-0.099Presentmethod0.8030.01697-0.094

图4 试验与本文方法计算的压力系数分布对比
Fig.4 Comparison of pressure coefficient between results of present method and experiment
4 跨声速翼型算例研究
首先不考虑翼型后缘连续变弯度,对翼型进行气动减阻的单点优化设计。本文进行两种思路的优化设计:一种是只考虑几何约束和气动力系数约束对初始翼型优化,得到无激波翼型[22],用Opt1表示;另一种是除考虑几何约束和气动力系数约束之外,还对压力分布形态进行约束,得到超临界翼型,用Opt2表示。无激波翼型在设计点具有较好的气动特性,但其非设计点的气动特性较差[23];相反,超临界翼型在设计点气动特性不是最优的,但通常是设计点与非设计点折中的设计结果。
在优化得到的翼型Opt1和Opt2的基础上,以后缘偏转角度为设计变量、以阻力系数最小为优化目标,针对不同的升力系数进行优化设计,研究后缘连续变弯度对翼型极曲线特性的影响。并根据优化结果深入分析后缘连续变弯度对这两种翼型极曲线特性的影响机理。
4.1 跨声速翼型单点优化设计

图5 初始翼型及其相应的EFFD控制框
Fig.5 Initial airfoil and EFFD control framework
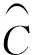
(4)
偏差W越小表明上表面压力系数分布越接近期望值,在优化设计中要求W<0.005。
综上,该优化问题的数学模型可描述为
minCD
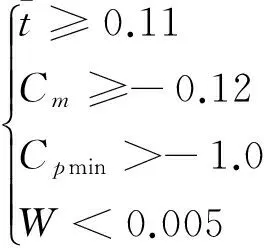
(5)
其中,最后两个约束条件仅在超临界翼型的优化设计中使用。
优化前后翼型的对比如图6所示;压力系数分布的对比如图7所示;气动力系数对比如表2所示。由图7可以看出,Opt1得到了无激波的压力分布,Opt2得到了典型的超临界翼型的压力分布。从表2可以看出,Opt1在设计点的阻力特性和俯仰力矩特性均好于Opt2。

图6 翼型几何外形对比
Fig.6 Comparison of geometric shape of airfoils
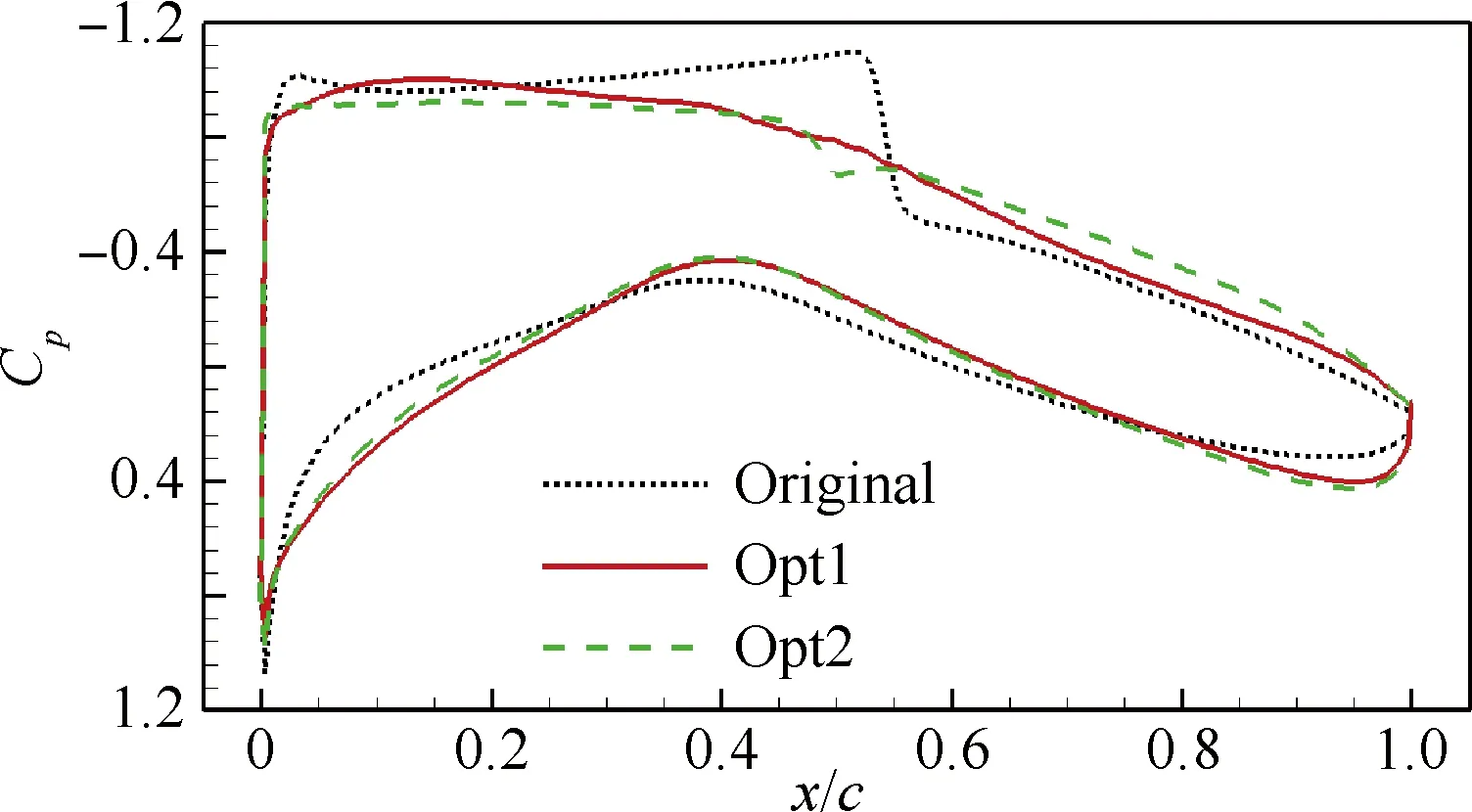
图7 翼型的压力系数对比
Fig.7 Comparison of pressure coefficient of airfoils

表2 翼型气动特性对比
为了更全面地对比这两个翼型的气动特性,分别对其设计点附近的气动特性进行评估。在设计升力系数下,Opt1和Opt2的阻力发散特性的对比如图8(a)所示;在设计马赫数下,Opt1和Opt2的极曲线特性的对比如图8(b)所示。从图8 中可以看出,相比于Opt2,Opt1对马赫数和升力系数的变化较为敏感,其阻力发散特性和极曲线特性均较差。

图8 翼型的气动特性对比
Fig.8 Comparison of aerodynamic characteristic of airfoils
4.2 后缘连续变弯度对翼型极曲线特性的影响
在优化得到的翼型Opt1和Opt2的基础上,研究后缘连续变弯度对翼型极曲线特性的影响。设计状态:Ma=0.74、Re=20.0×106时,CL=0.55,0.60,0.65,0.75,0.80,0.85。针对每个设计状态以后缘偏转角度为设计变量,以阻力系数最小为目标进行优化设计。优化得到的翼型分别命名为Opt3和Opt4。
翼型后缘变弯的范围参照现代民用客机机翼结构布置中后梁的弦向位置,柔性上蒙皮和刚性下蒙皮的范围定为弦长的73%~97%。
不同升力系数下,Opt3和Opt4的后缘几何外形如图9所示。从图9 中可以看出,当升力系数小于0.70时,后缘向上偏转,且升力系数越小上偏的角度越大;当升力系数大于0.70时,后缘向下偏转,且升力系数越大下偏的角度越大。
图9 翼型后缘放大图
Fig.9 Amplification of trailing-edge of airfoils
不同升力系数下,Opt3和Opt4的后缘偏转角度β如图10所示,其中后缘下偏为正。由图10 可以看出,后缘偏转角度在-1.5°~+1.5°之间,均在机构可以实现的偏转范围内。
优化前后翼型的极曲线特性对比如表3所示。从表中看出,升力系数小于0.70时,Opt3的极曲线特性明显提高,减阻最高达到3.9%,而Opt4的极曲线特性提高不明显;升力系数大于0.70时,Opt3和Opt4的极曲线特性都明显提高,减阻分别达到2.4%~18.1%和1.7%~13.2%。此外,升力系数小于0.70时,Opt3的极曲线特性比Opt2差,升力系数大于0.70时,Opt3的极曲线特性比Opt2好,但比Opt4的差。
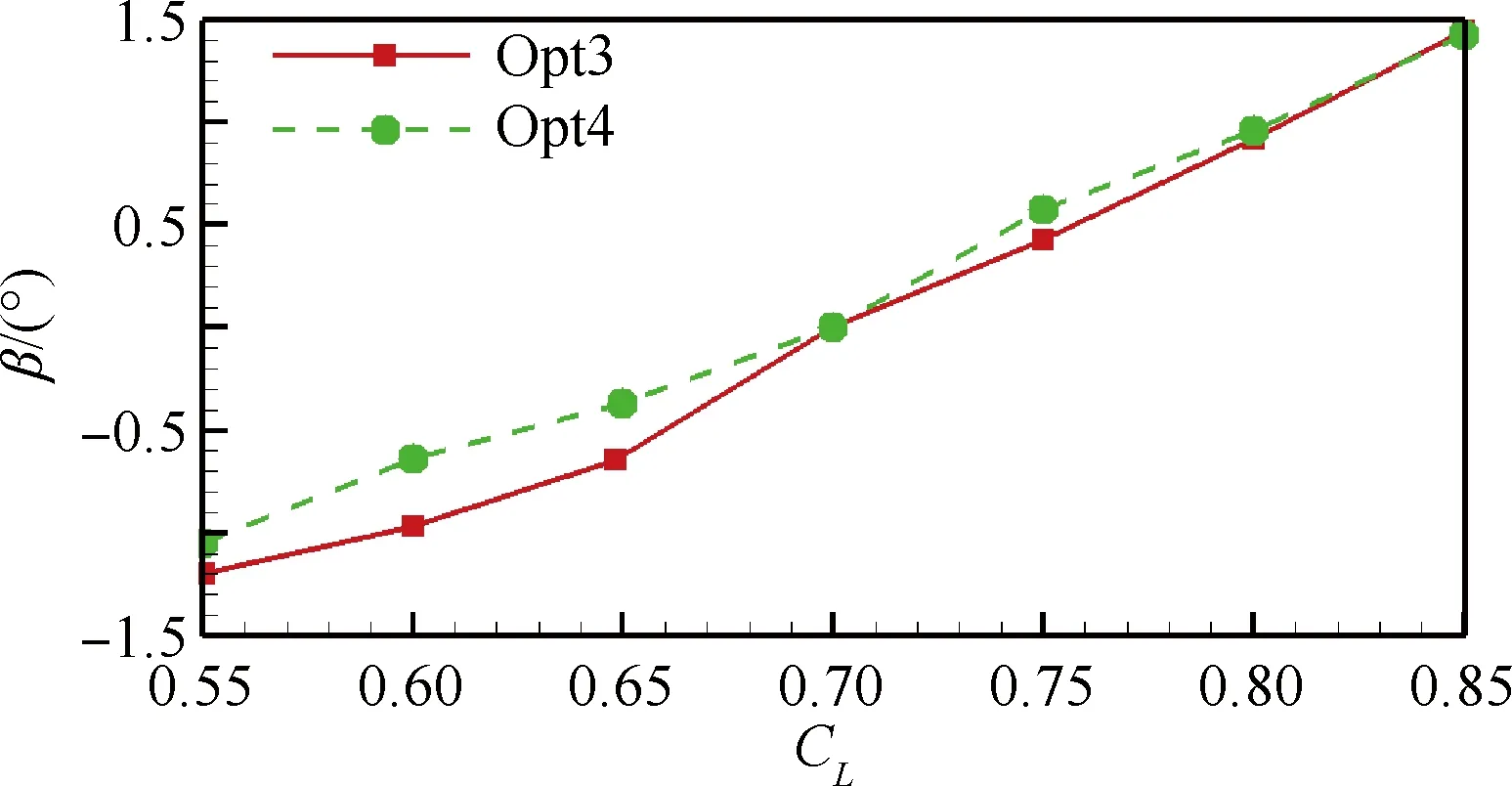
图10 翼型后缘偏转角度对比
Fig.10 Comparison of trailing-edge deflection of airfoils
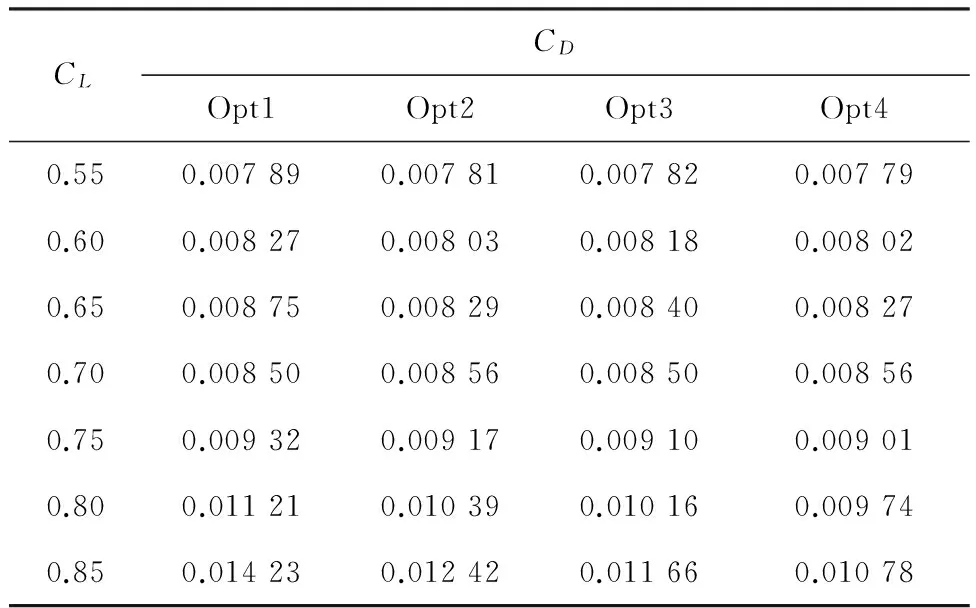
表3 翼型的极曲线特性对比
Opt1和Opt3的压力系数对比如图11(a)所示;Opt2和Opt4的压力系数对比如图11(b)所示。其中,在升力系数为0.70时,Opt1和Opt3以及Opt2和Opt4的压力系数是重合的。
下面针对不同升力系数下升阻特性改善的原因进行研究。
以升力系数CL=0.65为例解释当升力系数小于0.70时,后缘连续变弯度对气动特性的影响。从图11(a)可以看出,在升力系数为0.65时,Opt1计算的压力系数分布有明显的双激波特性,而且第2个激波的强度较大;Opt3计算的压力分布的第2个激波的强度明显减小,降低了激波阻力,进而改善了升阻特性。接下来对其产生机理进行深入分析。Opt1在设计升力系数下的压力系数分布是无激波的,当升力系数小于设计升力系数时,迎角减小,上翼面头部附近的气流加速区变短,使得气流的动能不足以维持超声速流动,在靠前的位置产生激波结束超声速流动,在激波后翼型后部曲率的增加使得气流出现了再加速,由于气流加速区较长,产生了第2个激波,且强度较大。翼型Opt3在Opt1的基础上后缘上偏,相当于减小了翼型的后加载,在相同升力系数下增加了迎角,使上翼面头部附近气流的加速区增加,增加了上翼面头部附近气流的动能,使得第1个激波后移;第1个激波位置的后移使激波后气流继续加速的区域变短,降低了第2个激波的强度,甚至可以消除第2个激波。Opt4的升阻特性没有大的改善主要是因为Opt2压力分布的鲁棒性较好,当升力系数小于设计升力系数时,不像无激波翼型那样产生明显的双激波特性的压力系数分布,而是仅产生较弱的2次加速的压力系数分布形态,如图11(b)所示。

图11 压力系数对比
Fig.11 Comparison of pressure coefficients
以升力系数CL=0.75为例解释当升力系数大于0.70时,后缘连续变弯度对气动特性的影响。从图11 中可以看出,在升力系数为0.75时,Opt3和Opt4的激波强度较小,降低了激波阻力,从而改善了该点的气动特性。接下来对其产生机理进行深入分析。翼型Opt3(Opt4)在Opt1(Opt2)的基础上后缘下偏,相当于增加了翼型后加载,降低了巡航迎角。巡航迎角的降低使上翼面头部附近的气流加速区变短,降低负压峰值并使得上翼面激波之前维持一个较高的压力系数。同时后缘下偏增加了流经上翼面后缘气流的扩张速度,使得后缘压力系数恢复的梯度增加。综合以上两个原因,后缘下偏一方面使上翼面的激波强度减弱,另一方面使上翼面激波位置后移。
仔细观察图11,可以发现,在不同的升力系数下,Opt1和Opt2的头部峰值变化较明显;而Opt3和Opt4的头部峰值变化较小,且翼型前25%弦长的压力系数基本重合。下面对其产生机理进行分析。当升力系数大于0.70时,Opt3和Opt4的后缘下偏,增加了翼型的弯度,进而在相同升力系数下降低了迎角;当升力系数小于0.70时,Opt3和Opt4的后缘上偏,减小了翼型的弯度,进而在相同升力系数下增加了迎角。优化后缘偏转角度的结果显示,在不同的升力系数下,Opt3和Opt4的迎角变化很小(如图12所示),而翼型的负压峰值与迎角紧密相关,因此,在不同的升力系数下,Opt3和Opt4的负压峰值基本保持不变。

图12 迎角对比
Fig.12 Comparison of angles of attack
5 结 论
1) 在跨声速流动状态下,无激波翼型与超临界翼型相比,其设计点的气动特性较好,但阻力发散特性和极曲线特性较差;与他人已发表过文献的结论一致。
2) 升力系数小于单点优化设计升力系数时,后缘上偏有利于极曲线特性的提高,原因是增加了迎角,使第一个激波位置后移,缩短了激波后气流加速的区域,降低了第二个激波的强度,从而使得阻力系数降低,此外,超临界翼型由于鲁棒性较好,没有产生明显的双激波,因而阻力系数降低不明显。
3) 升力系数大于单点优化设计升力系数时,后缘下偏有利于极曲线特性的提高,原因是减小了迎角,使上翼面激波之前维持一个较高的压力系数,进而降低了上翼面激波的强度,与此同时也使得激波位置后移。
[1] URNES J, NGUYEN N, IPPOLITO C, et al. A mission adaptive variable camber flap control system to optimize high lift and cruise lift-to-drag ratios of future n+3 transport aircraft[C]//51th AIAA Aerospace Sciences Meeting. Reston: AIAA, 2013: 1-7.
[2] JAMES M, URNES J, CHARLES M. Control system design for a variable camber continuous trailing edge flap system on an elastic wing[C]//55th AIAA/ ASME/ASCE/AHS/SC Structures, Structural Dynamics, and Materials Conference. Reston: AIAA, 2014: 1-13.
[3] RENEAUX J. Overview on drag reduction technologies for civil transport aircraft[C]//European Congress on Computational Methods in Applied Sciences and Engineering. Jyväskylä: ECCOMAS, 2004: 7-24.
[4] KOTA S. Shape control of adaptive structures using compliant mechanisms: AFRLSR-BL-TR-00-0125[R]. Ann Arbor: Department of Mechanical Engineering and Applied Mechanics, 2000.
[5] KERR-JIA L, KOTA S. Design of compliant mechanisms for morphing stricture shapes[J]. Journal of Intelligent Material Systems and Structures, 2003, 14(6): 379-391.
[6] DI-MATTEO N, GUO S, AHMED S, et al. Design and analysis of a morphing flap structure for high lift wing[C]//51th AIAA/ASME/ASCE/AHS/-ASC Structures, Structural Dynamics, and Material Conference. Reston: AIAA, 2010: 4-12.
[7] YOKOZEKI T, SUGIURA A. Development of variable camber morphing airfoil using corrugated structure[J]. Journal of Aircraft, 2014, 51(3): 1023-1029.
[8] YOKOZEKI T, SUGIURA A. Development and wind tunnel test of variable camber morphing wing[C]//22nd AIAA/ASME/AHS Adaptive Structures Conference. Reston: AIAA, 2014: 1-13.
[9] KAUL K, NGUYEN N. Drag optimization study of variable camber continuous trailing tdge flap using overflow[C]//32nd AIAA Applied Aerodynamics Conference. Reston: AIAA, 2014: 6-16.
[10] 杨智春, 解江. 柔性后缘自适应机翼的概念设计[J]. 航空学报, 2009, 30(6): 1028-1034. YANG Z C, XIE J. Concept design of adaptive wing with flexible trailing edge[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(6): 1028-1034 (in Chinese).
[11] 杨智春, 党会学, 解江. 基于动网格技术的柔性后缘自适应机翼气动特性分析[J]. 应用力学学报, 2009, 26(3): 548-554. YANG Z C, DANG H X, XIE J. Aerodynamic characteristics of flexible trailing edge adaptive wing by unstructured dynamic meshes[J]. Chinese Journal of Applied Mechanics, 2009, 26(3): 548-554 (in Chinese).
[12] 陈钱, 白鹏, 尹维龙, 等. 可连续光滑偏转后缘的变弯度翼型气动特性分析[J]. 空气动力学报. 2010, 28(1): 46-53. CHEN Q, BAI P, YIN W L, et al. Analysis on the aerodynamic characteristics of variable camber airfoils with continuous smooth morphing trailing edge[J]. Acta Aerodynamica Sinica, 2010, 28(1): 46-53 (in Chinese).
[13] 孔博, 王福新, 周涛. 基于环量控制无缝变弯度翼型的气动设计[J]. 空气动力学报, 2013, 31(5): 583-586. KONG B, WANG F X, ZHOU T. The aerodynamic design of seamlessly camber-variable airfoil based on circulation control[J]. Acta Aerodynamica Sinica, 2013, 31(5): 583-586 (in Chinese).
[14] 黄杰, 葛文杰, 杨方. 实现机翼前缘形状连续变化柔性机构的拓扑优化[J]. 航空学报, 2007, 28(4): 988-992. HUANG J, GE W J, YANG F. Topology optimization of the compliant mechanism for shape change of airfoil leading edge[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(4): 988-992 (in Chinese).
[15] 赵飞, 葛文杰, 张龙. 某无人机柔性机翼后缘变形机构的拓扑优化[J]. 机械设计, 2009, 26(8): 19-22. ZHAO F, GE W J, ZHANG L. Topological optimization on the deformation mechanism of flexible trailing edge of certain pilot-less aircraft[J]. Journal of Machine Design, 2009, 26(8): 19-22 (in Chinese).
[16] 王婷, 王帮峰, 芦吉云, 等. 一种拓扑优化方法在机翼可变后缘中的研究[J]. 机械科学与技术, 2011, 30(1): 1660-1663. WANG T, WANG B F, LU J Y, et al. The study of a topological optimization method on the adaptive wing’s trailing edge[J]. Mechanical Science and Technology for Aerospace Engineering, 2011, 30(1): 1660-1663 (in Chinese).
[17] 尹维龙, 石庆华, 田冬奎. 变体后缘的索网传动机构设计与分析[J]. 航空学报, 2013, 34(8): 1824-1831. YIN W L, SHI Q H, TIAN D K. Design and analysis of transmission mechanism with cable networks for morphing trailing edge[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(8): 1824-1831 (in Chinese).
[18] 刘卫东, 丁倩, 朱华, 等. 基于超声电机的变弯度翼的驱动与集成[J]. 振动、测试与诊断. 2013, 33(5): 856-861. LIU W D, DING Q, ZHU H, et al. Drive and integration techniques of variable camber wing based on ultrasonic motors[J]. Journal of Vibration, Measurement and Diagnosis, 2013, 33(5): 856-861 (in Chinese).
[19] SANTINI G M. Wing variable camber trailing edge tip: USA. US8844879[P]. 2014-09-30.
[20] 何小龙, 白俊强, 夏露, 等. 基于EFFD方法的自然层流短舱优化设计[J]. 航空动力学报, 2014, 29(10): 2311-2320. HE X L, BAI J Q, XIA L, et al. Natural laminar flow nacelle optimization design based on EFFD method[J]. Journal of Aerospace Power, 2014, 29(10): 2311-2320 (in Chinese).
[21] COOK P H, MCDONALD M A, FIRMIN M C P. Aerofoil RAE 2822-pressure distributions, and boundary layer and wake measurements: AGARD AR-138[R]. Neuilly Sur Seine, France: AGARD, 1979.
[22] PAINCHAUD-OUELLET S, TRIBES C, TREPANIER J Y, et al. Airfoil shape optimization using a nonuniform rational B-splines parameterization under thickness constraint[J]. AIAA Journal, 2006, 44(10): 2170-2178.
[23] 张宇飞. 基于先进CFD方法的民用客机气动优化设计[D]. 北京:清华大学, 2010. ZHANG Y F. Aerodynamic optimization of civil aircraft design based on advanced computational fluid dynamics[D]. Beijing: Tsinghua University, 2010 (in Chinese).
[24] 杨昆淼, 张卫民, 王斌. 基于机翼气动设计准则的超临界机翼气动优化研究[J]. 航空学报, 2013, 34(2): 263-272. YANG K M, ZHANG W M, WANG B. Research of super-critical wing optimization based on aerodynamic design principle of wing[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(2): 263-272 (in Chinese).
郭同彪 男, 硕士研究生。主要研究方向: 飞行器气动优化设计。
Tel: 15809270907
E-mail: 812558997@qq.com
白俊强 男, 博士, 教授, 博士生导师。主要研究方向: 飞行器总体气动布局设计、部件气动力设计、多学科优化设计、计算流体力学理论和应用。
Tel: 029-88492174
E-mail: junqiang@nwpu.edu.cn
Received: 2015-03-09; Revised: 2015-04-21; Accepted: 2015-05-23; Published online: 2015-06-24 15:03
URL: www.cnki.net/kcms/detail/11.1929.V.20150624.1503.001.html
Foundation item: National Basic Research Program of China (2014CB744800)
*Corresponding author. Tel.: 029-88492174 E-mail: junqiang@nwpu.edu.cn
Influence of continuous trailing-edge variable camber onaerodynamic characteristics of transonic airfoils
GUO Tongbiao, BAI Junqiang*, YANG Tihao
SchoolofAeronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China
The influence of continuous trailing-edge variable camber on the aerodynamic characteristics of transonic airfoils is investigated. Before the continuous trailing-edge variable camber is considered, the aerodynamic drag reduction optimization design of the transonic airfoil is carried out based on the optimization design system constructed in this paper. With different constraints added, two kinds of transonic airfoils are obtained, namely the shock-free airfoil and the supercritical airfoil. Then the optimization design is conducted based on the two airfoils at different lift coefficients, by taking the deflection angle of the trailing-edge as the design variable and the minimum drag coefficient as the objective. And the effect of the continuous trailing-edge variable camber on the drag polar of these two kinds of transonic airfoils is investigated and analyzed according to the optimization results. The results of the optimization design show that the aerodynamic characteristics of the shock-free airfoil are better than those of the supercritical airfoil at the design point, but the robustness is worse. Besides, when the lift coefficient is lower than the design lift coefficient, the drag polar characteristic of the shock-free airfoil can be improved greatly with the continuous trailing-edge variable camber applied, thus the drag coefficient is reduced by up to 3.9%. However, the situation of supercritical airfoil is different. The results also demonstrate that when the lift coefficient exceeds the design lift coefficient, the continuous trailing-edge variable camber method can significantly improve the drag polar performance of both airfoils with the drag coefficients of them being reduced by 2.4%-18.1% and 1.7%-13.2% respectively.
continuous trailing-edge variable camber; shock-free airfoil; supercritical airfoil; optimization design; robustness; polar
2015-03-09;退修日期:2015-04-21;录用日期:2015-05-23; < class="emphasis_bold">网络出版时间:
时间: 2015-06-24 15:03
www.cnki.net/kcms/detail/11.1929.V.20150624.1503.001.html
国家“973”计划 (2014CB744800)
.Tel.: 029-88492174 E-mail: junqiang@nwpu.edu.cn
郭同彪, 白俊强, 杨体浩. 后缘连续变弯度对跨声速翼型气动特性的影响[J]. 航空学报, 2016, 37(2): 513-521. GUO T B, BAI J Q, YANG T H. Influence of continuous trailing-edge variable camber on aerodynamic characteristics of transonic airfoils[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 513-521.
http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn
10.7527/S1000-6893.2015.0161
V211.41+2
: A
: 1000-6893(2016)02-0513-09
*
