GAW-1翼型前后缘变弯度气动性能研究

陆维爽， 田云， 刘沛清， 王涛， 张良富

1.北京航空航天大学 大型飞机高等人才培训班， 北京 100083 2.北京航空航天大学 航空科学与工程学院， 北京 100083

GAW-1翼型前后缘变弯度气动性能研究

陆维爽1， 田云1， 刘沛清2,*， 王涛1， 张良富1

1.北京航空航天大学 大型飞机高等人才培训班， 北京 100083 2.北京航空航天大学 航空科学与工程学院， 北京 100083

传统增升装置主要用于提高飞机起降气动性能。利用计算流体力学(CFD)的方法，引入了通用飞机翼型的前后缘变弯装置的概念，数值模拟了GAW-1翼型在爬升状态时，前缘变弯装置、后缘襟翼/副翼偏转以及前后缘装置综合偏转对翼型气动特性的影响。研究表明，前缘变弯装置可以有效地改善翼型的失速特性，失速迎角提高了3°左右，最大升力系数提高了4.56%；同时提高升阻比50%～120%；但在设计升力系数下，升力系数和阻力系数都略微减小。另一方面，后缘变弯装置可以改变最大升阻比所对应的迎角，以及在小迎角时，提高升力系数6%左右。翼型综合偏转可以在小迎角时增加升力系数，在大迎角时增加升阻比。

通用飞机； 前缘下垂； 后缘襟翼； 副翼； 变弯度； 气动性能

飞机在起降、巡航时的飞行效率是通用飞机机翼设计的重要考虑因素，由此可设计出飞机机翼的高升力构型以及干净构型。在实际的飞行过程中，飞机的飞行条件不断发生着变化，而机翼构型却基本不变。机翼前后缘变弯装置不仅参考了现代军用飞机的机动襟翼及大型客机增升装置概念，还尽可能地提高了任务剖面的飞行效率，其在通用飞机机翼设计中具有很好的应用前景。

长期以来，前后缘变弯装置已经在各类飞机上得到了广泛的应用，国外研究中比较具有代表性的有，美国国家航空航天局(NASA)在航空学基金组织的的支持下，研究的“可连续变弯的后缘襟翼”(Variable Camber Continuous Trailing Edge Flap，VCCTEF)[1-4],初步研究结果表明可连续变弯度的后缘襟翼实现减阻达到6.31%，并且提高升阻比达到4.85%。与此同时，欧洲空中客车公司(Airbus)、德国宇航中心(DLR)等13家欧洲机构合作的“未来智能增升装置”项目，分别研究了智能前缘(Smart Leading Edge，SLE)和智能单缝襟翼(Smart Single Slotted Flap，SSSF)这2种变弯装置，但是关于这2种变弯装置的气动数据较少[5-12]。Li等[13]延用这一概念，进行了气动弹性分析。除此以外，Yokozeki和Sugiura[14-15]设计了波浪结构机翼后缘，以达到机翼后缘变弯度的目的。而国内方面，陈钱[16]和尹维龙[17]等主要针对翼型后缘变弯度进行了气动性能的研究。

基于前后缘变弯装置现有的研究情况，本文利用前后缘增升装置改变翼型的弯度，前缘采用前缘下垂式的变弯装置，后缘采用富勒襟翼以及副翼变弯装置，这样的设计利用了现有的增升装置，尽可能避免由此带来的额外负担。针对GAW-1翼型，设计了前缘下垂、后缘襟翼偏转、副翼偏转以及前后缘综合偏转等不同的构型方案，并对其进行了计算流体力学(CFD)分析，结果表明采用前后缘增升装置综合偏转可以明显改善翼型的爬升性能。

1 计算模型与方法

计算采用结构网格以及Fluent作为求解器。为了验证数值模拟的可靠性，选择使用30P30N翼型进行验证计算。网格的拓扑结构如图1所示，壁面第一层网格高度为1×10-5倍的参考弦长。

图1 30P30N翼型近壁网格

Fig.1 Closeup of grid for 30P30N airfoil

考虑到与试验值对比，相关外部流场模拟参数为：马赫数Ma=0.20，雷诺数Re=9×106，迎角α=0°～24°，来流压力为常压。由此得出的计算弦长c=1.9 m。

Fluent的求解设置为隐式算法、耦合式求解器(Coupled Solver)，湍流模型采用一方程Spalart-Allmaras(S-A)模型，S-A模型是专门用于处理具有壁面边界的空气流动问题的[18]，方程中的动量和湍流动能均采用二阶迎风格式处理。

图2为计算和试验得到的升力系数CL的对比，在α≤19°时，翼型总的升力系数随着迎角增大而增大，与试验值吻合良好，前缘缝翼、主翼和后缘襟翼单独的气动力也与试验值吻合良好；在α>19°后，前缘缝翼升力系数的计算值偏大，多段翼型总升力系数的计算值偏大，失速迎角大约后移2°，失速迎角在23° 附近。图3为迎角为8°时翼型表面压力系数Cp的分布对比，主翼和襟翼吻合得很好，缝翼的上翼面吻合得较好。

图2 数值模拟和风洞试验获得的升力系数对比

Fig.2 Comparison of lift coefficients between numerical simulation and wind tunnel test

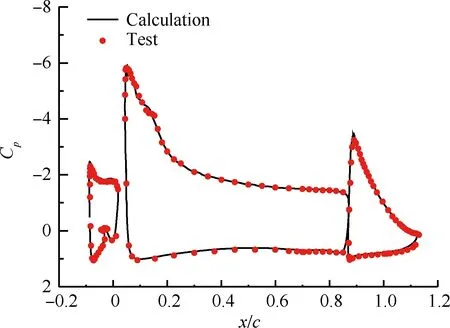
图3 数值模拟和风洞试验获得的压力系数分布对比

Fig.3 Comparison of pressure coefficients distribution between numerical simulation and wind tunnel test

进一步通过速度型的对比验证算法的可靠性，如图4所示，α=8°时，在x=0.45c，0.898 17c，1.032 1c，1.112 5c这4个代表性的位置做翼型的横截面测得沿该直线方向的速度型分布。其中，纵坐标指从翼型表面开始沿着垂线方向的距离(n/c)，横坐标指所测速度与远场速度的比值(V/V∞)。

在图4中，试验与数值模拟中襟翼边界层、主翼边界层与主翼的尾迹都可以清楚地看到，而数值模拟出来的前缘的尾迹速度损失比试验值明显。在α=8°下，主翼段(x=0.45c)的边界层比较饱满且统一，而襟翼段与之相反。这与压力系数曲线显示的在小迎角下襟翼上载荷大的现象相一致。在襟翼段(x=0.898 17c,1.032 1c,1.112 5c)显示了在襟翼表面有逆压梯度的趋势。主要表现在主翼段的尾迹在襟翼上产生轻微的分离、尾迹变厚及随着弦线长度增长尾迹速度型降低。总体来说，数值模拟结果与试验结果吻合得较好。

综上所述，数值模拟结果是可信的。

图4 翼型截面速度型分布

Fig.4 Speed profile distribution of airfoil section

2 前缘变弯度对气动性能的影响

本文选取的分析模型为GAW-1翼型，其最大厚度为17%c[19]。GAW-1翼型是先进的通用飞机翼型，其气动特性包括：具有大的上表面前缘半径，以减小大迎角下的负压峰值，推迟翼型失速；上表面比较平坦，使升力系数为0.4时，上表面有均匀的载荷分布；下表面后缘有较大弯度。

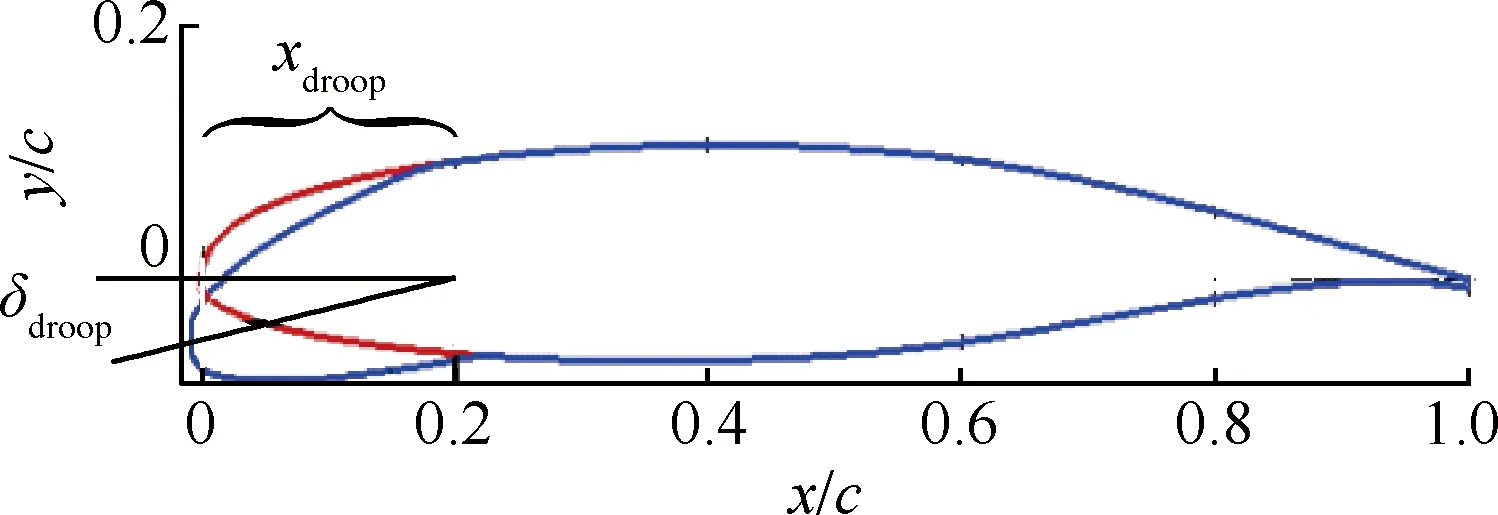
图5 具有前缘下垂的翼型

Fig.5 Airfoil with leading-edge droop nose

针对GAW-1干净翼型，改变前缘的下垂角度与下垂弦长，铰链前缘下垂依靠简单铰链机构下偏，其运动轨迹为一段圆弧。由于翼型气动性能受上翼面影响较大，因此下垂弦长这一参数以上翼面为标准，并通过计算求出下翼面转轴位置。铰链前缘下垂的设计参数如图5所示，其中:xdroop为铰链前缘下垂弦长与当地机翼弦长之比；δdroop为铰链前缘下垂角。

分别针对下垂角度为3°、6°、9°、12°、15°，下垂弦长为0.10c、0.12c、0.14c、0.16c、0.18c、0.20c的不同参数工况进行了CFD计算分析。计算的来流条件为：马赫数Ma=0.189，雷诺数Re=8.8×106，迎角α=-4°～20°，来流压力为常压。

2.1 前缘下垂角对气动性能的影响

固定前缘下垂弦长为0.18c，下垂角为3°、6°、9°、12°、15°，图6为气动力计算结果。

由图6(a)和图6(b)可以看出，随着前缘下垂角增加，失速迎角增加，失速迎角由原始干净翼型的15°，最大增加到17°，且前缘下垂翼型升力系数在迎角小于10°时，比干净翼型小2.86%，而当迎角大于10°时，随着下垂角增加，升力系数增大，最大升力系数最多增加4.56%；同时，在迎角小于10°时，阻力系数CD大于干净翼型，在迎角为8°时增加1.77%，而当迎角大于10°时，随着前缘下垂角增加，阻力系数显著减小，但当下垂角大于9°时，随着下垂角的增加，阻力系数的减幅渐小。

图6 前缘下垂角对气动力的影响

Fig.6 Effect of different leading-edge droop angles on aerodynamic force

图7为不同前缘下垂角对升阻比K的影响。可以看出，当升力系数小于1.75时，随下垂角增加，升阻比减小，但在升力系数最大处，升阻比随下垂角增加而增大，并且下垂角越大，最大升力系数越大。图8为不同前缘下垂角对俯仰力矩系数Cm的影响，可以看出，随下垂角增加，翼型低头力矩增大。

由图9压力系数分布曲线可以看出，随着下垂角增加，前缘吸力峰逐渐降低，并且在前缘下垂圆弧运动轨迹过渡区域逐渐形成第2个吸力峰，因此使得逆压梯度降低，延缓上翼面流动分离，增加失速迎角；随着下垂角增加，第2个吸力峰逐渐增强，当下垂角大于10°时，前缘吸力峰消失，第2个吸力峰渐强，前后缘压差又逐渐增加，因此当下垂角大于10°后，随下垂角增加，阻力系数减小不明显；由于前缘下垂后，前缘吸力损失，使得抬头力矩减小，低头力矩增大。

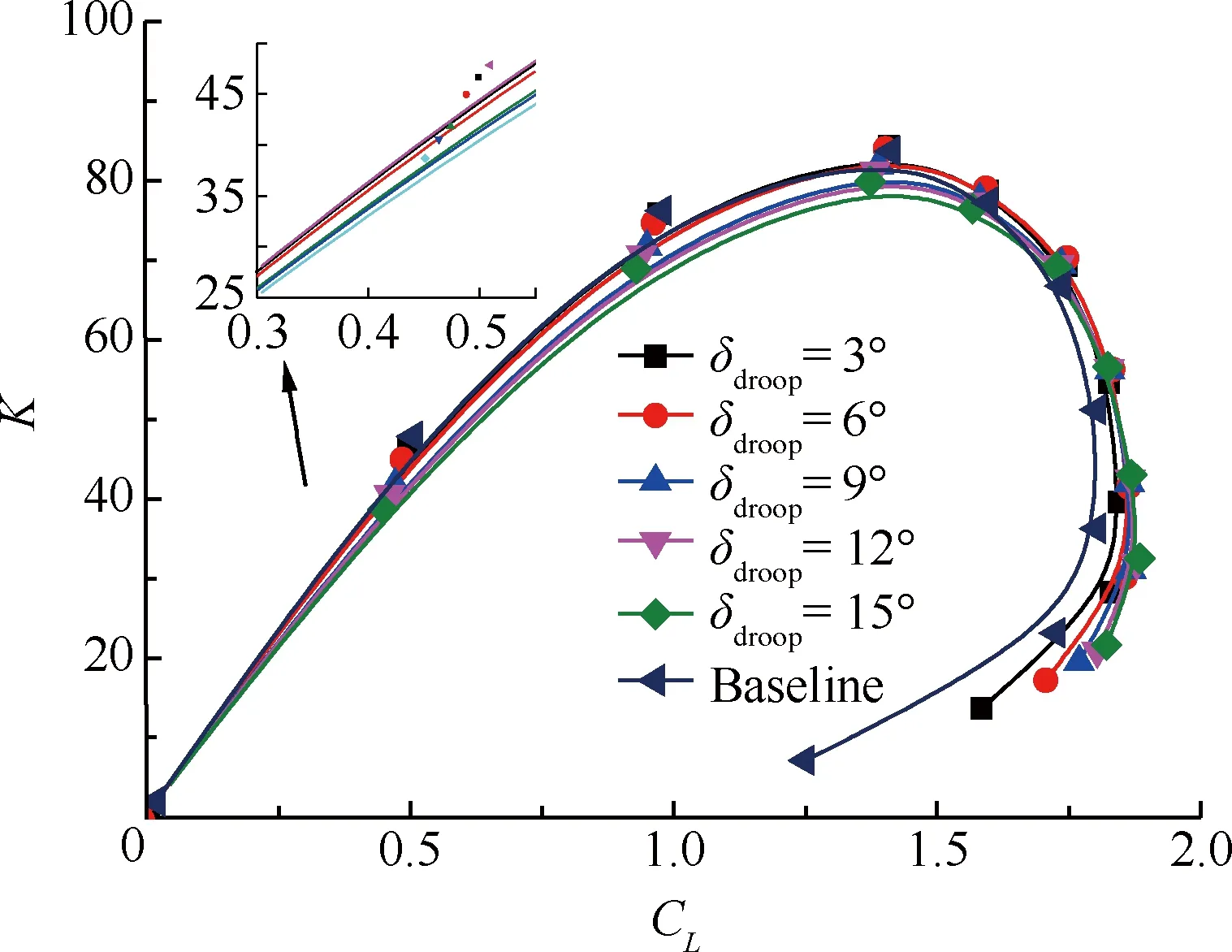
图7 前缘下垂角对升阻比的影响

Fig.7 Effect of different leading-edge droop angles on lift-drag ratio

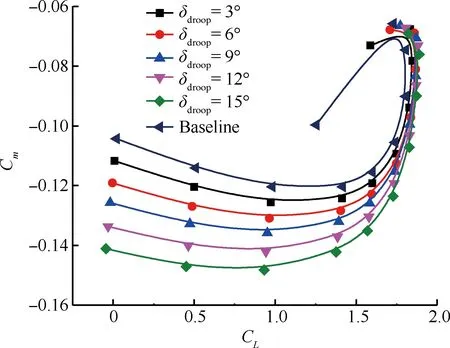
图8 前缘下垂角对俯仰力矩系数的影响

Fig.8 Effect of different leading-edge droop angles on pitching moment coefficient

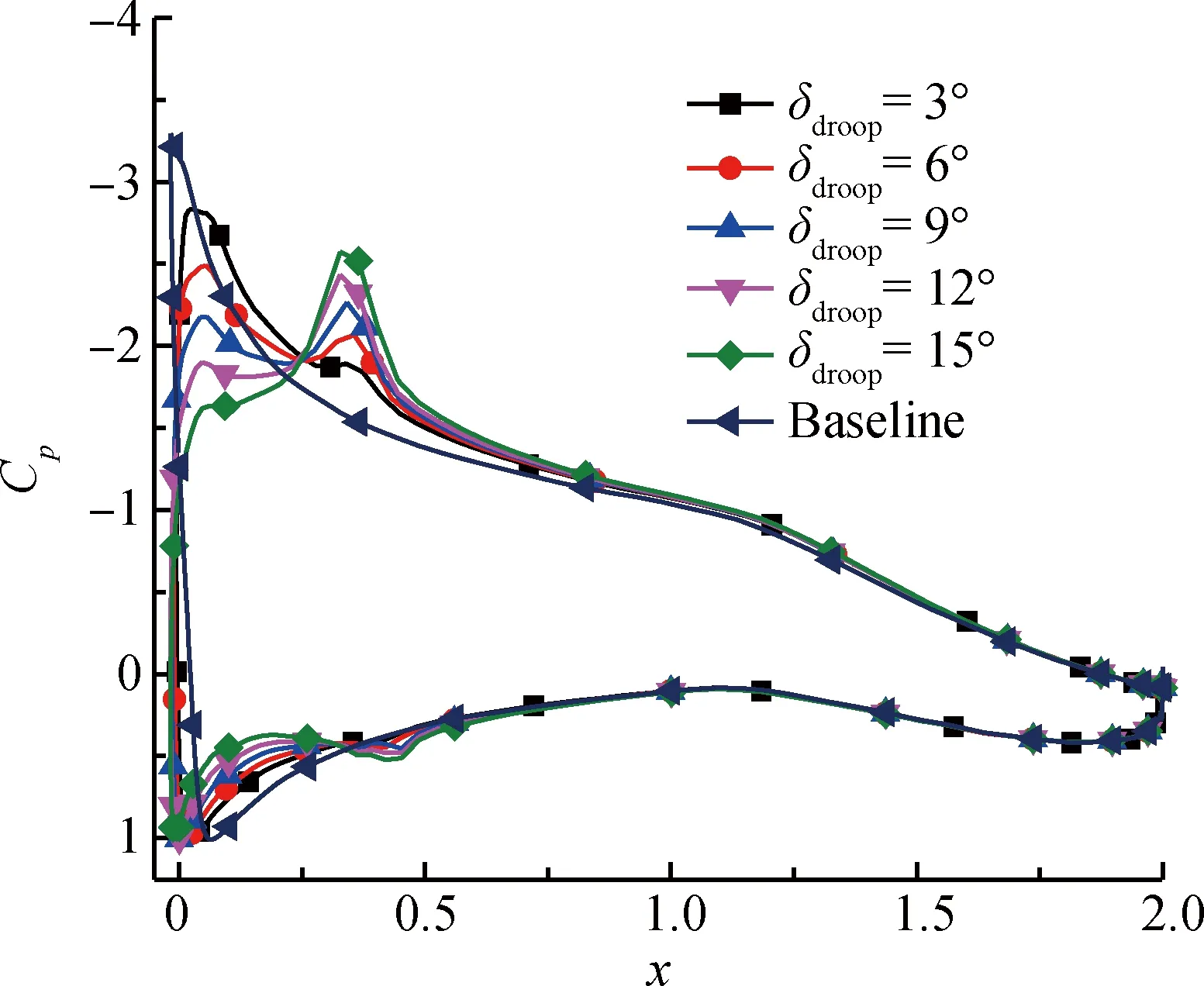
图9 前缘下垂角对压力系数分布的影响

Fig.9 Effect of different leading-edge droop angles on pressure coefficient distribution

2.2 前缘下垂弦长对气动性能的影响

固定前缘下垂角为12°，下垂弦长分别为0.10c、0.12c、0.14c、0.16c、0.18c、0.20c。图10为相应的气动力计算结果。可以看出，随着前缘下垂弦长增加，失速迎角逐渐增加，失速迎角由原始干净翼型的15°最大增加到18°，并且在迎角小于10°时，升力系数比干净翼型小2.62%，而当迎角大于10°时，升力系数逐渐增大，最大升力系数最多增加3.65%；同时，在迎角小于10°时，前缘下垂阻力系数较干净翼型增加了1.48%，而当迎角大于10°时，阻力系数显著减小。

图10 前缘下垂弦长对气动力的影响

Fig.10 Effect of different leading-edge droop chords on aerodynamic force

图11为不同前缘下垂弦长对升阻比的影响。由图可以看出，当升力系数小于1.6时，随下垂弦长增加，升阻比逐渐减小，但在升力系数最大处随着下垂弦长增加，升阻比增大。图12为不同前缘下垂弦长对俯仰力矩系数的影响，可以看出，随下垂弦长增加，翼型低头力矩增大。

由图13压力系数分布曲线可以看出，随着下垂弦长增加，前缘吸力峰逐渐降低，并且在前缘下垂圆弧运动轨迹过渡区域逐渐形成第2个吸力峰，且第2个吸力峰随下垂弦长增加，位置后移，因此使得逆压梯度降低，从而增加失速迎角；随着下垂弦长增加，第二个吸力峰逐渐减弱；由于前缘下垂后，前缘弯度减小，前缘吸力损失，使得抬头力矩减小，低头力矩增大。

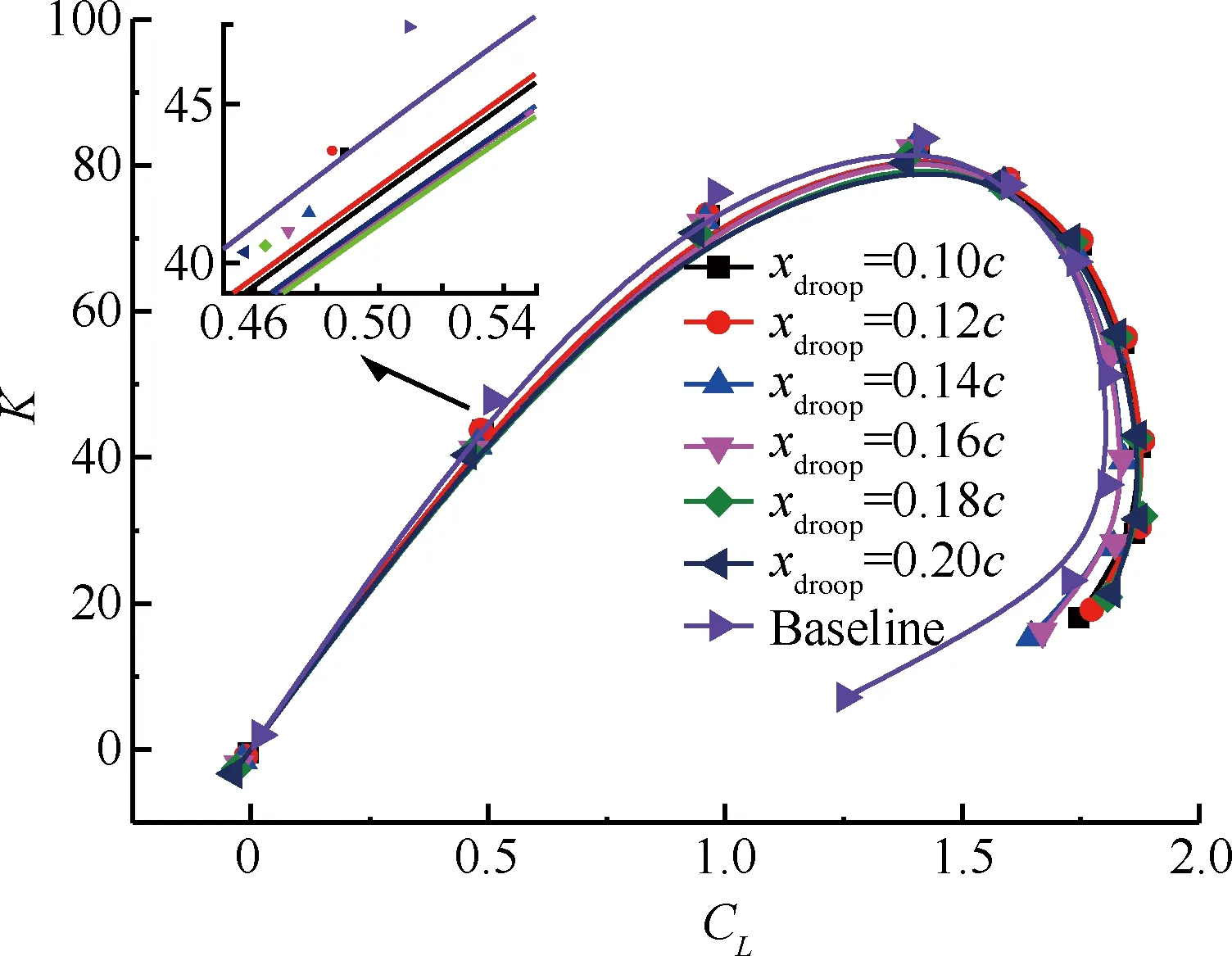
图11 前缘下垂弦长对升阻比的影响

Fig.11 Effect of different leading-edge droop chords on lift-drag ratio

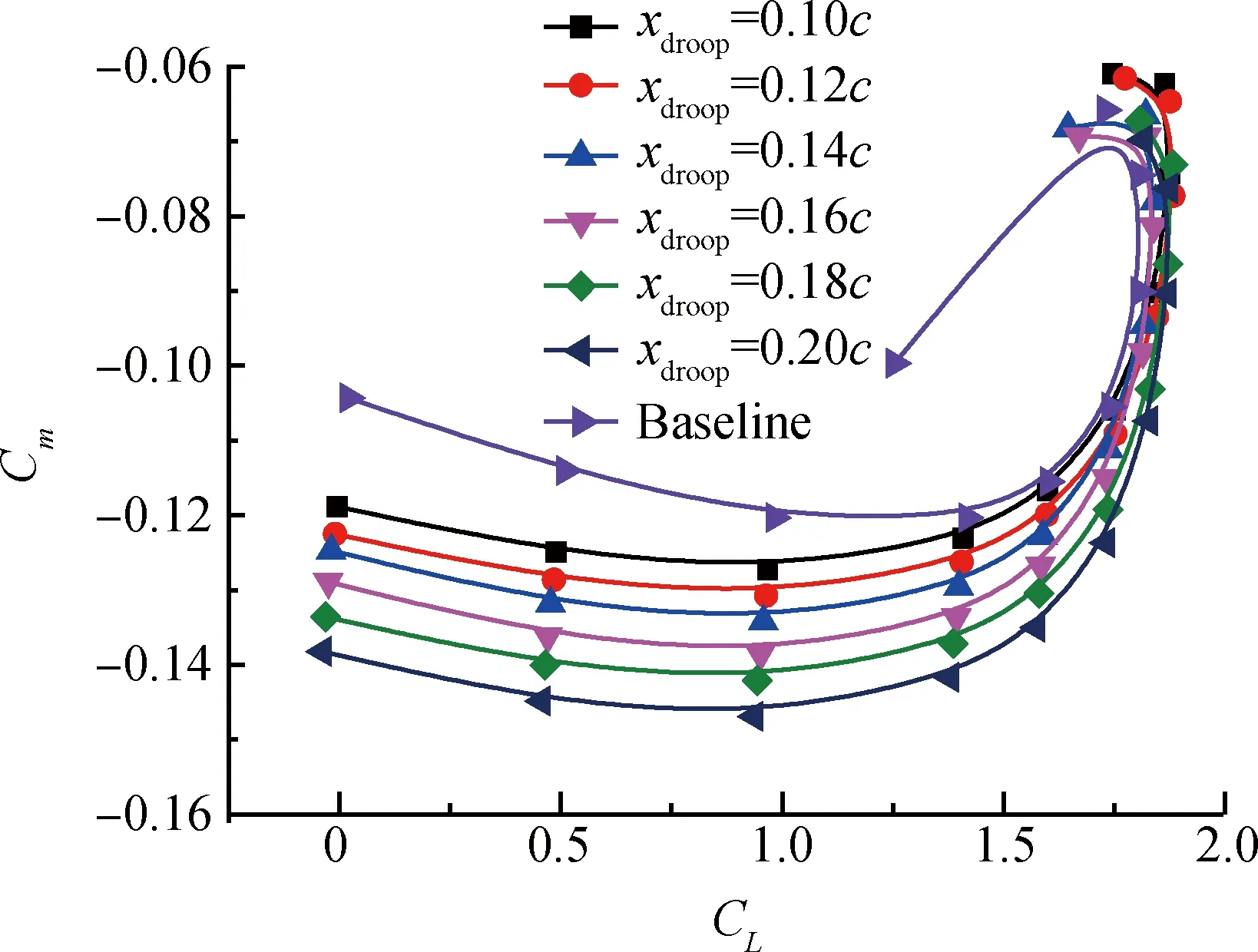
图12 前缘下垂弦长对俯仰力矩系数的影响

Fig.12 Effect of different leading-edge droop chords on pitching moment coefficient

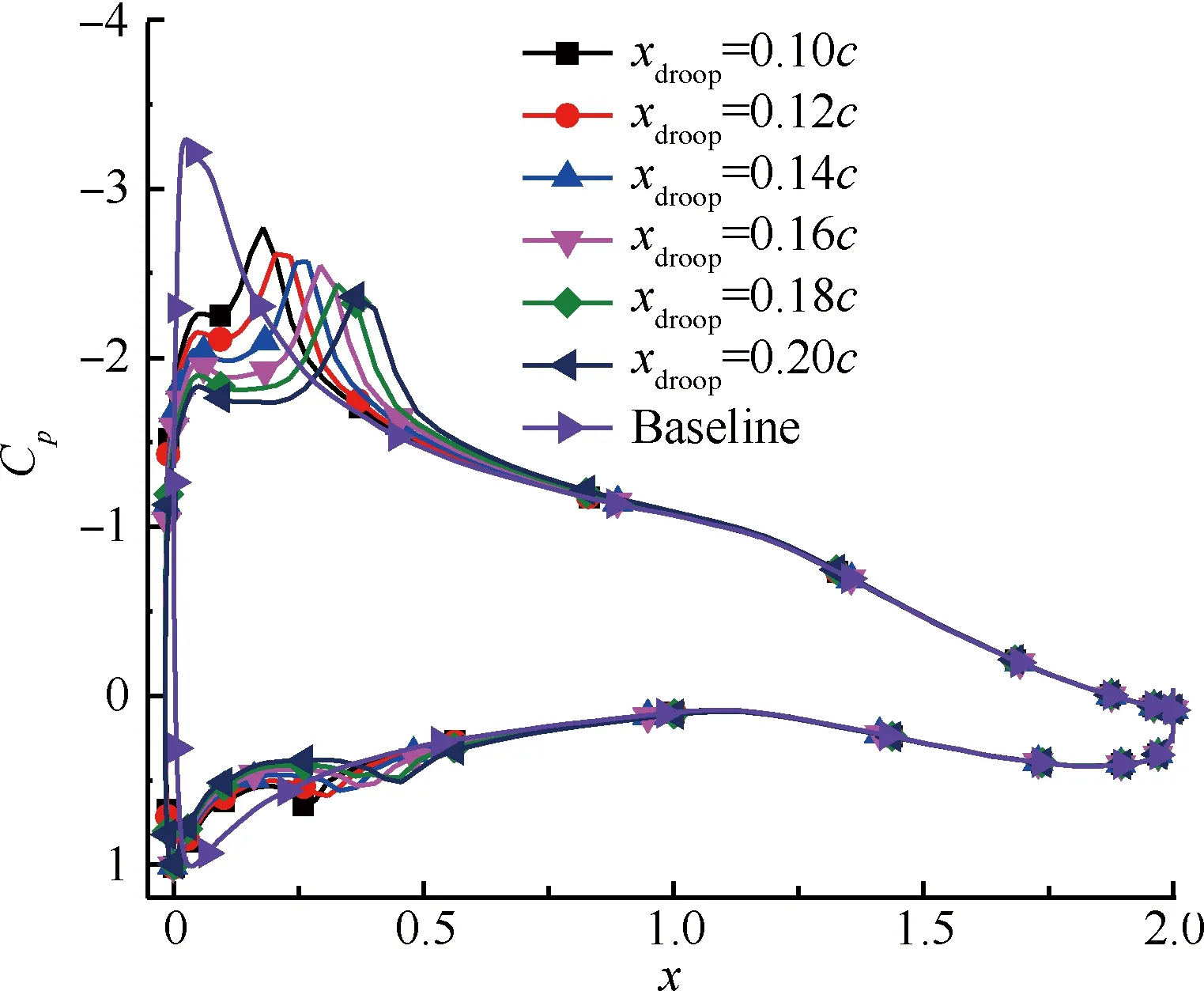
图13 前缘下垂弦长对压力系数分布的影响

Fig.13 Effect of different leading-edge droop chords on pressure coefficient distribution

3 后缘变弯度对气动性能的影响

针对GAW-1干净翼型，改变后缘襟翼以及副翼偏转的角度，其中襟翼弦长固定为30%c[20]，副翼弦长为20%c[19]。翼型襟翼以及副翼的设计参数如图14和图15所示，图中:δflap为襟翼偏转角；δaileron为副翼偏转角。富勒襟翼每偏转1°，襟翼后退0.15%c，同时保持襟翼的上翼面与主翼上翼面过渡尽量光滑。计算的来流条件为：马赫数Ma=0.189，雷诺数Re=8.8×106，迎角α=-4°～20°，来流压力为常压。

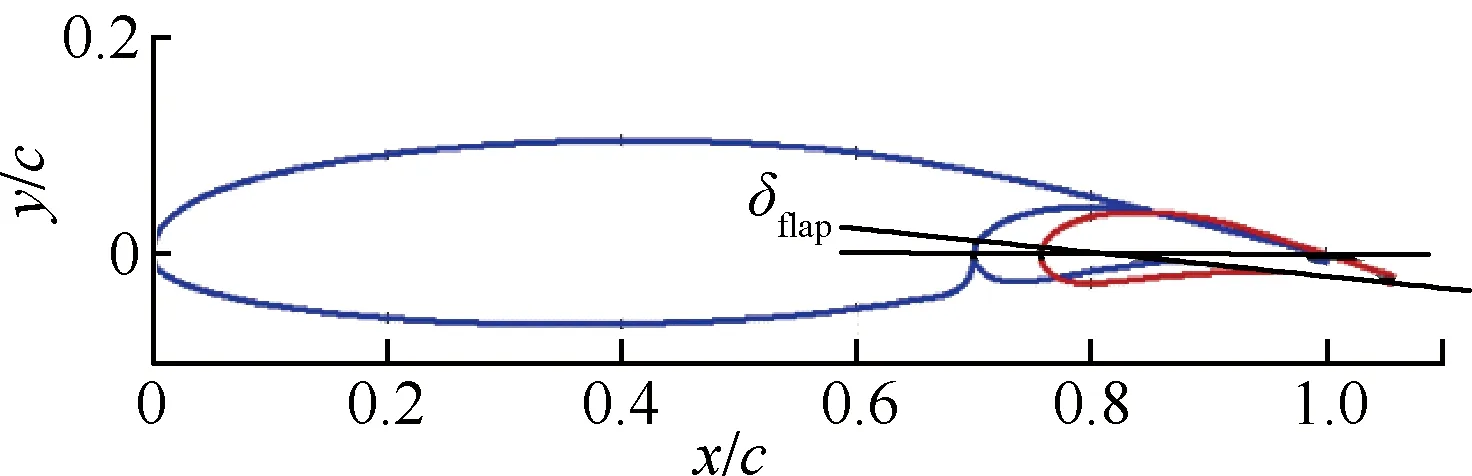
图14 具有30%c襟翼的翼型

Fig.14 Airfoil with 30%c flap

图15 具有20%c副翼的翼型

Fig.15 Airfoil with 20%c aileron

分别针对襟翼偏转角为1°、2°、3°、4°(向下)，副翼偏转角为-2°、-4°、-6°(向上)、2°、4°、6°(向下)的工况进行CFD计算。

3.1 后缘襟翼偏转对气动性能的影响

襟翼偏转角为1°、2°、3°、4°时，气动力计算结果如图16所示。由升力系数与阻力系数曲线可以看出，随着襟翼偏转角的变化，翼型的有效弯度也随之变化，翼型的升力系数、阻力系数随弯度的增加而增加。在小迎角时，升力系数增加的幅度较大，并且增幅维持在一个常数;阻力系数也随着下偏角的增大而增大，增大的幅度呈线性。而在大迎角时，升力系数增加的幅度变小；阻力系数增加的幅度较大。同时，失速迎角随着向下偏转角的增加而减小。

图17为不同襟翼偏转角对升阻比的影响。由图可以看出，在升力系数小于1.2时，升阻比的变化不是十分明显，有效弯度越大，相应的升阻比略小。这是因为偏转角的改变，使得升力系数和阻力系数同时增加或者减少，并且升力系数的增幅几乎为常数，而阻力系数的增幅是线性增大的。同时，从图17中不难看出，随着襟翼下偏角的增大，最大升阻比也随之略有增大，所对应的迎角略有减小。图18为不同襟翼偏转角对俯仰力矩系数的影响，可以看出，随着襟翼向下偏转角的变大，俯仰力矩系数越大。这是因为襟翼向下偏转角越大，襟翼的弯度越大，翼型尾部产生的升力也会随之增加。

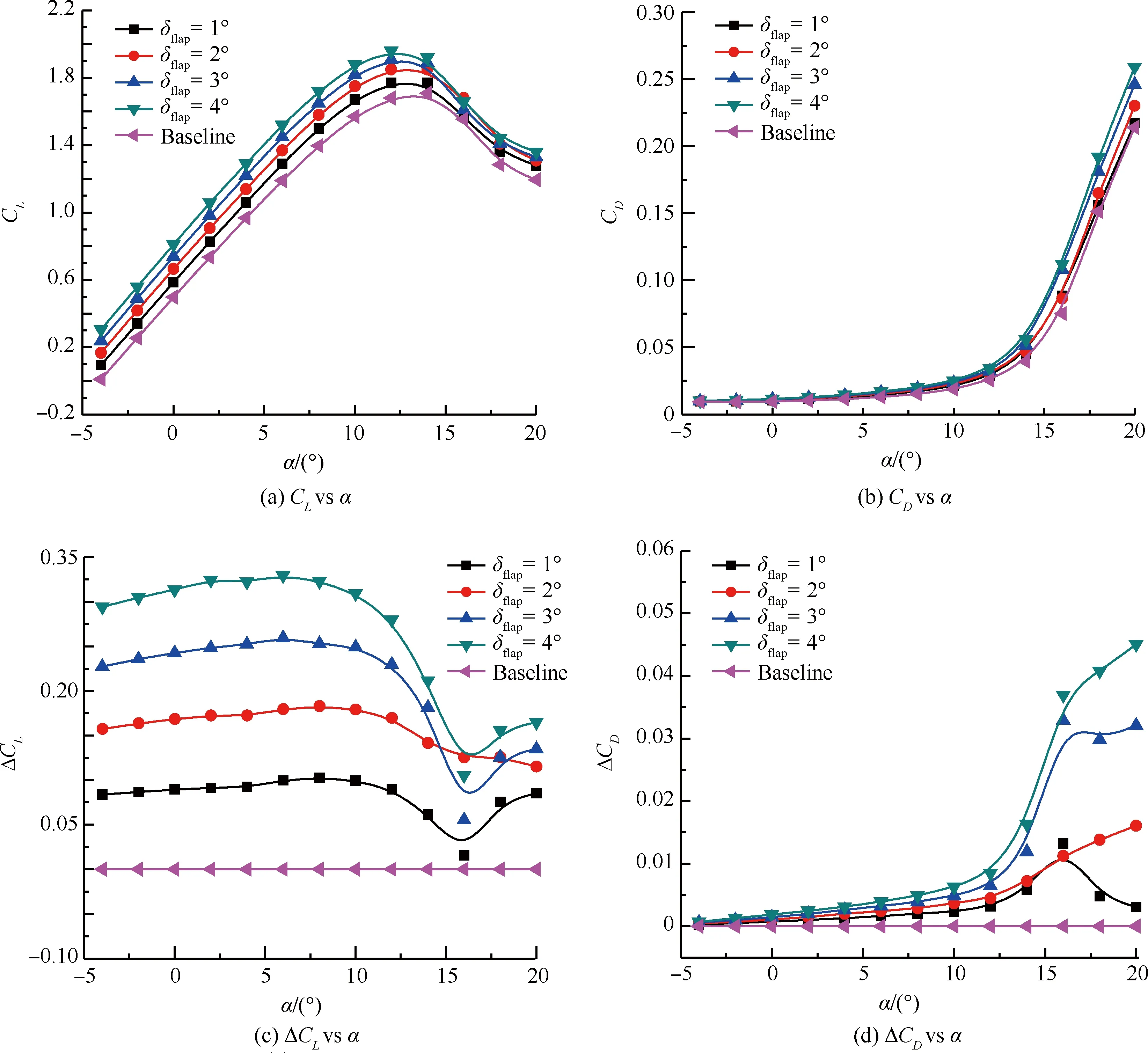
图16 襟翼偏转角对气动力的影响

Fig.16 Effect of different angles of flap on aerodynamic force

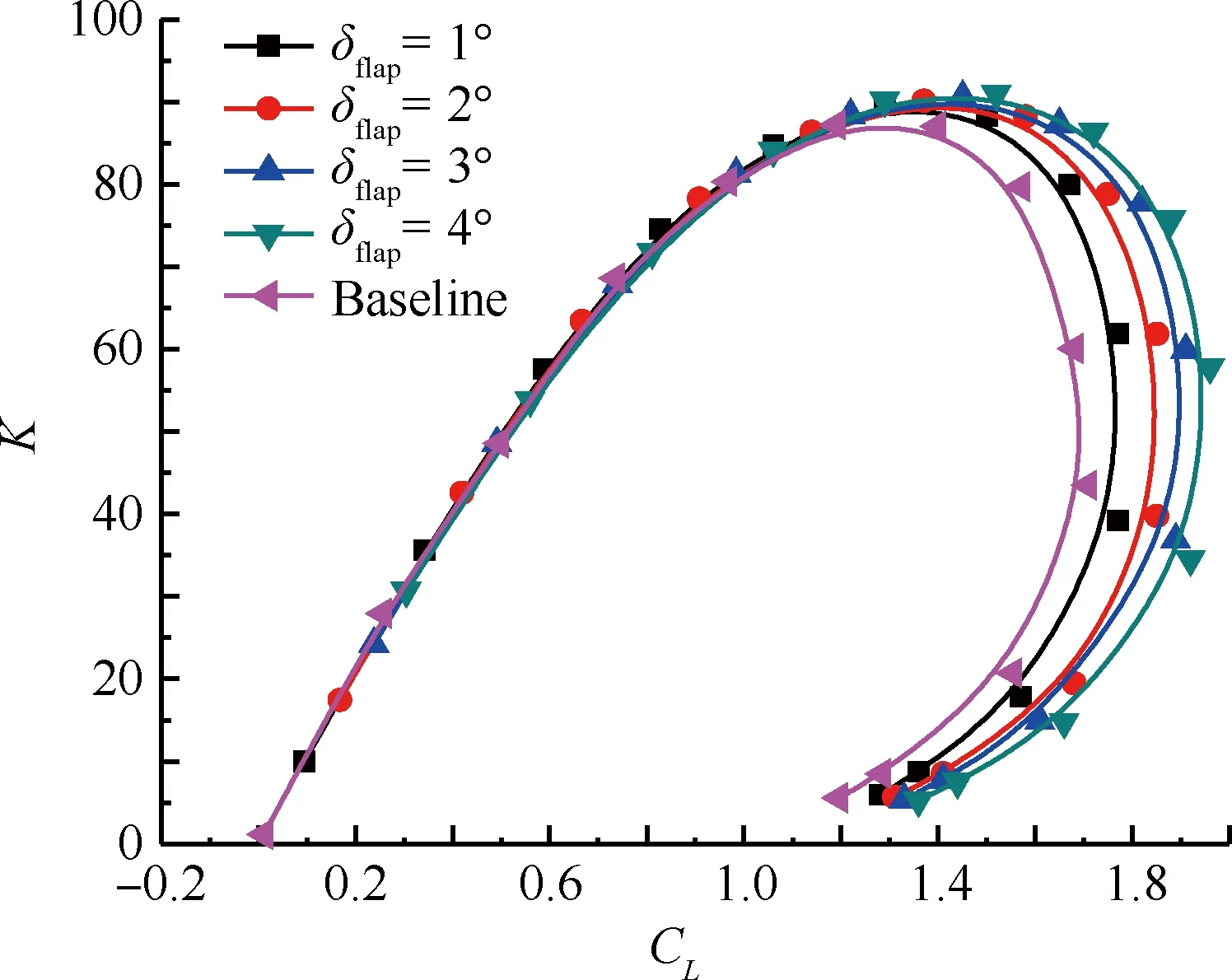
图17 襟翼偏转角对升阻比的影响

Fig.17 Effect of different angles of flap on lift-drag ratio

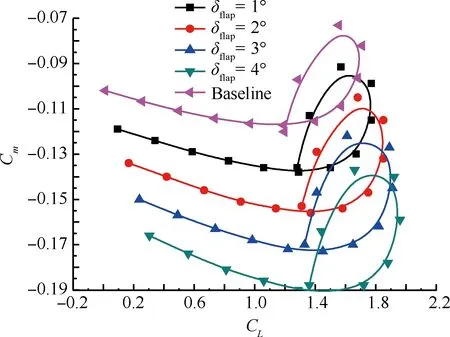
图18 襟翼偏转角对俯仰力矩系数的影响

Fig.18 Effect of different angles of flap on pitching moment coefficient

由图19的压力系数分布曲线可以看出，随着襟翼向下偏转角的变大，翼型上翼面的负压值越大，下翼面的正压值也越大。这都是翼型的有效弯度改变而导致的现象。

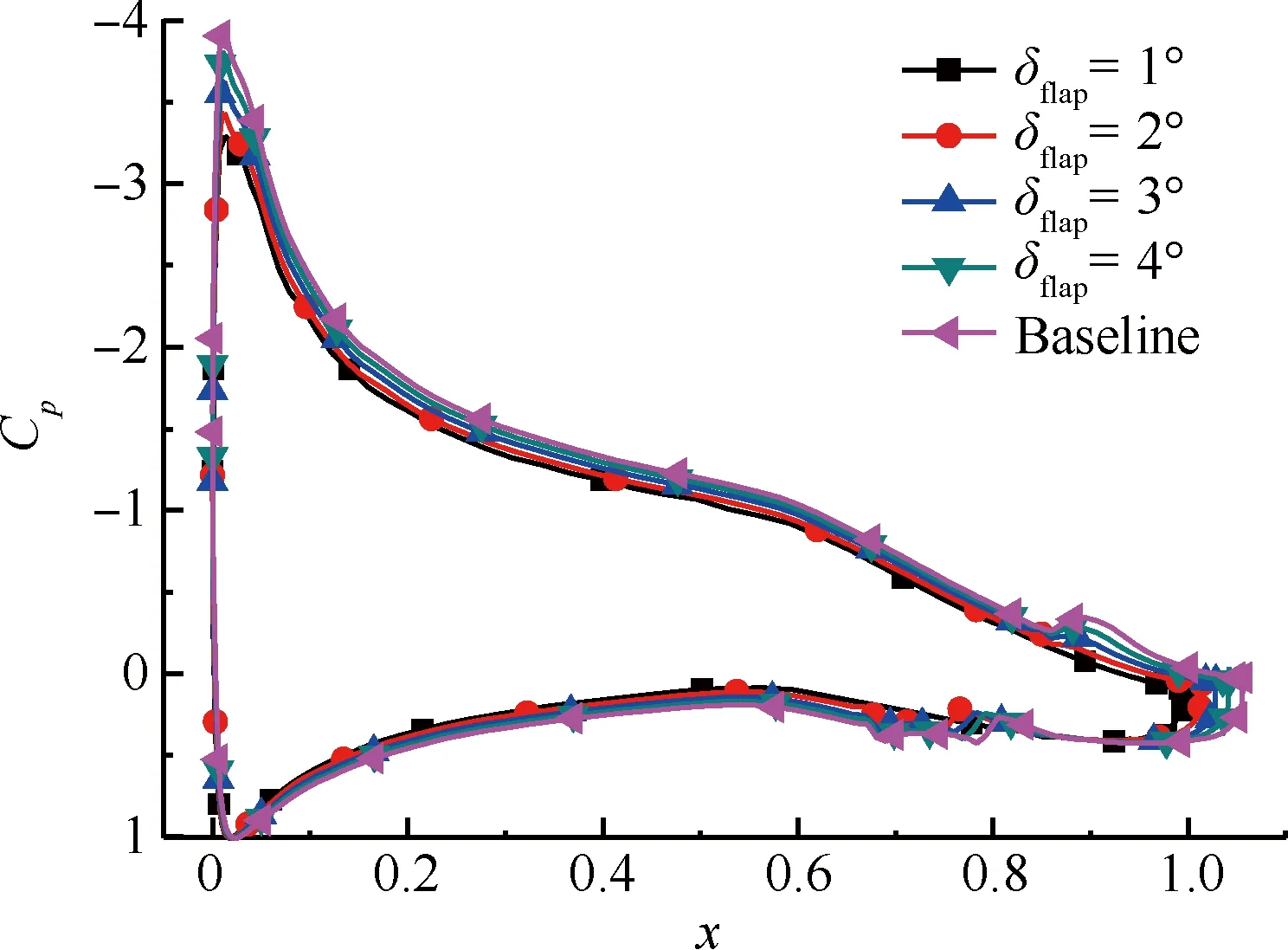
图19 襟翼偏转角对压力系数分布的影响

Fig.19 Effect of different angles of flap on pressure coefficient distribution

3.2 后缘副翼偏转对气动性能的影响

副翼偏转角为2°、4°、6°、-2°、-4°、-6°时，气动力计算结果如图20所示。由升力系数与阻力系数曲线可以看出，随着副翼偏转角的变化，翼型的有效弯度也随之变化，弯度越大，翼型的升力系数、阻力系数越大。在小迎角时，升力系数增加的幅度较大，随着迎角的增大，升力系数增加的幅度略有减小;阻力系数增大的幅度呈线性。而在大迎角时，升力系数增加的幅度明显变小；阻力系数增加的幅度明显增大。同时，副翼上偏时，失速迎角变大；副翼下偏时，失速迎角减小。机理和襟翼偏转相同，是因为翼型有效弯度增大，提前发生流动分离，产生失速现象。

图21为不同副翼偏转角对升阻比的影响。由图可以看出，在升力系数小于1.1时，升阻比K的变化不是十分明显，有效弯度越大，相应的升阻比略小。这是因为偏转角的改变，使得升力系数和阻力系数同时增加或者减少，并且升力系数的增幅在减小，而阻力系数的增幅在增大。同时，从图21中不难看出，随着副翼偏转角的改变，最大升阻比几乎不变，相应的，最大升阻比对应的迎角随着有效弯度的增加而略有减小。图22为不同副翼偏转角对俯仰力矩系数的影响，可以看出，副翼上偏时，低头力矩减小；副翼下偏时，低头力矩增大。这是因为副翼的偏转改变了翼型尾部的流场，导致升力随之改变，副翼向下偏转的越大，升力越大。

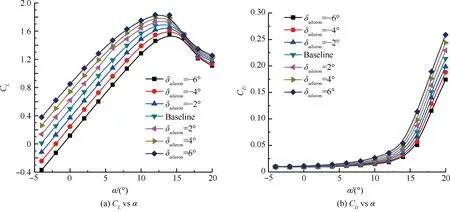
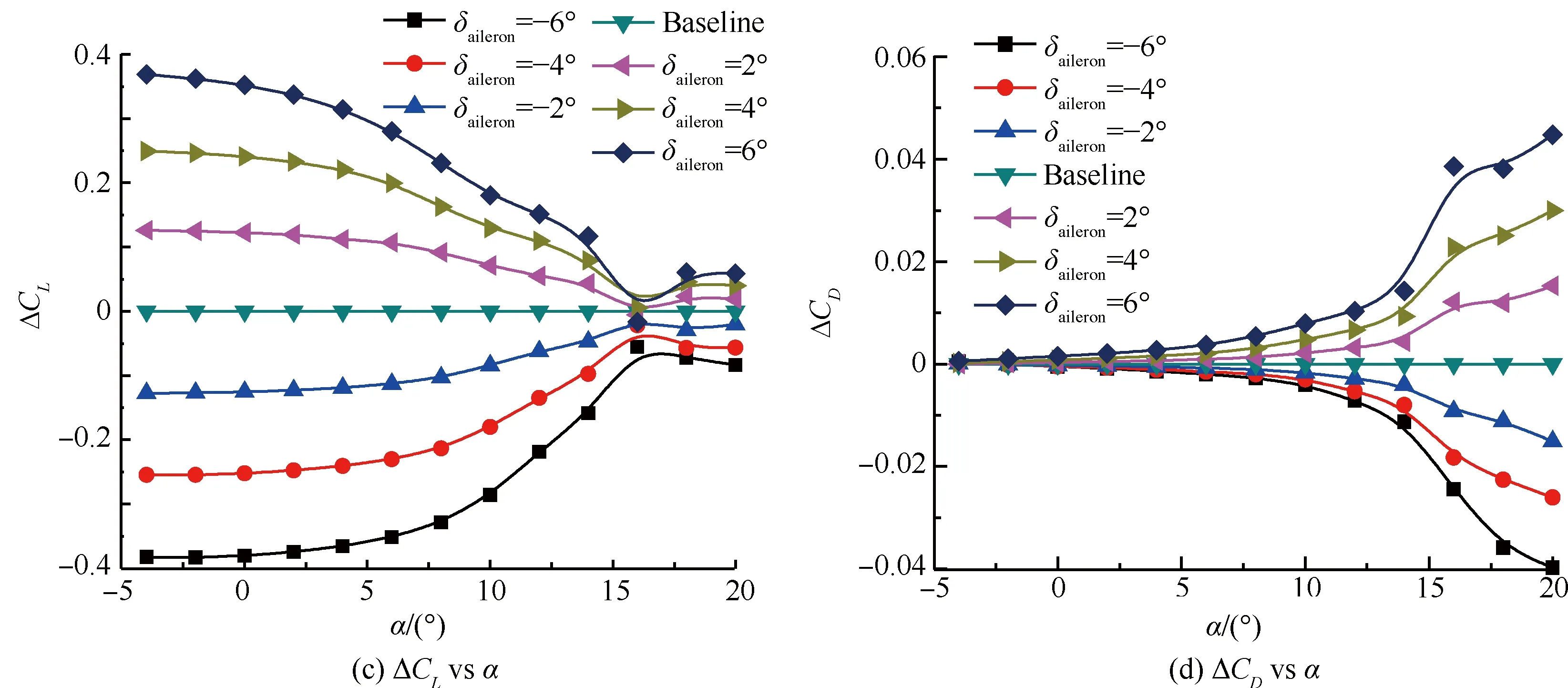
图20 副翼偏转角对气动力的影响

Fig.20 Effect of different angles of aileron on aerodynamic force

由图23的压力系数分布曲线可以看出，副翼向下偏转角越大，翼型的有效弯度就越大，其上翼面的负压值越大，下翼面的正压值也越大。其机理与襟翼偏转相同。

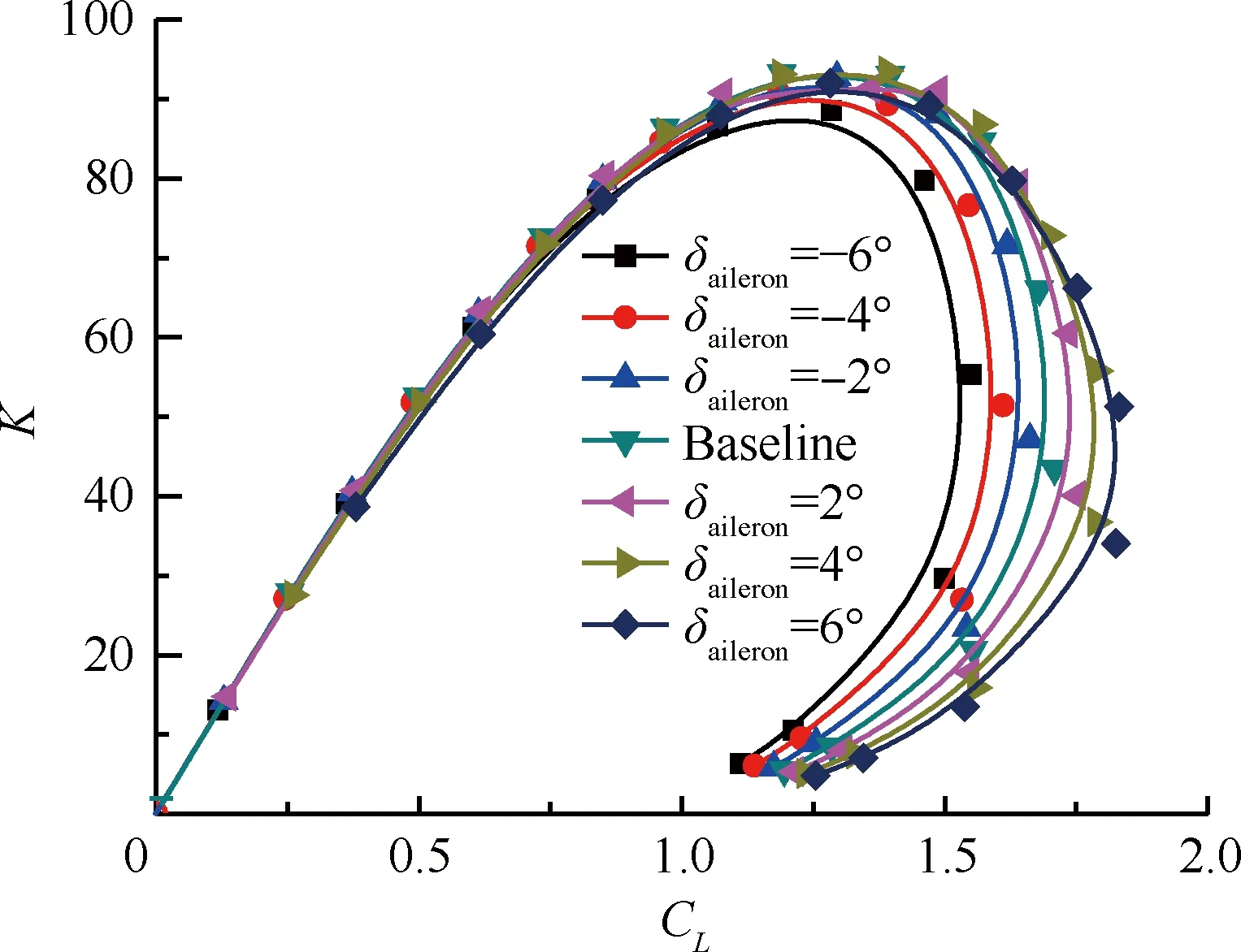
图21 副翼偏转角对升阻比的影响

图22 副翼偏转角对俯仰力矩系数的影响

图23 副翼偏转角对压力系数分布的影响

Fig.23 Effect of different angles of aileron on pressure coefficient distribution

4 前后缘综合偏转对气动性能的影响

如图24所示，前缘下垂弦长为参考弦长的18%，后缘采用30%c的富勒襟翼。同时偏转GAW-1翼型的前后缘装置，改变翼型的弯度，通过CFD方法模拟爬升条件下的气动特性。计算的来流条件为：马赫数Ma=0.189，雷诺数Re=8.8×106，迎角α=-4°～20°，来流压力为常压。

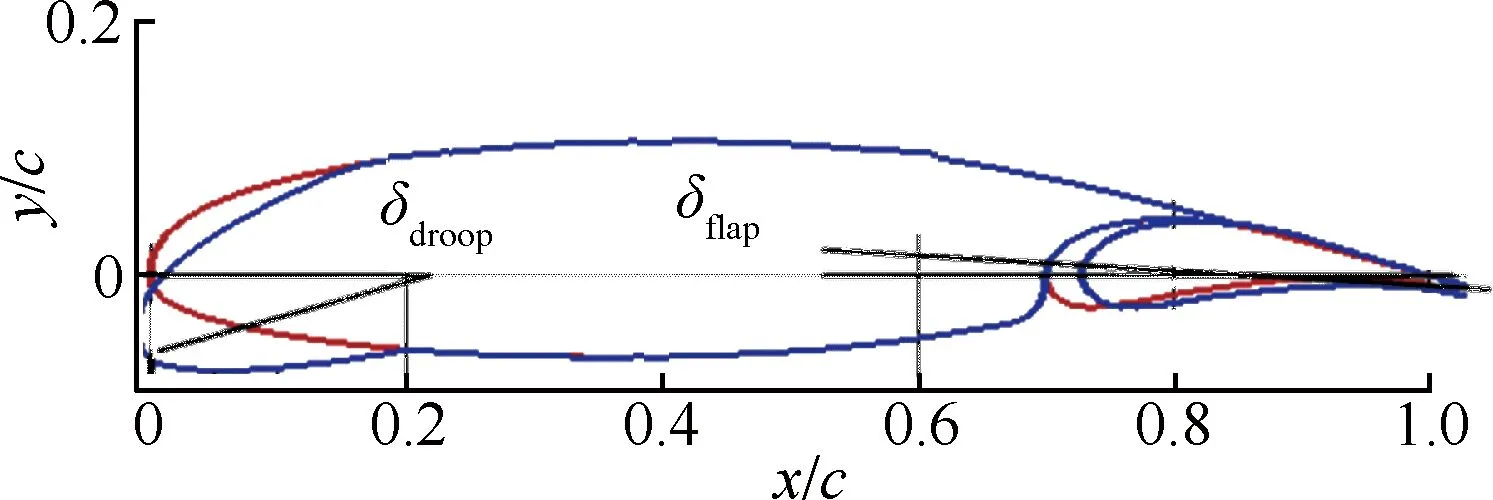
图24 具有前缘下垂和后缘襟翼的翼型

Fig.24 Airfoil with leading-edge droop nose and trailing-edge flap

4.1 固定前缘时后缘下偏角对气动性能的影响

选定δdroop为6°，δflap分别为1°、2°、3°，CFD计算的气动力结果如图25所示。

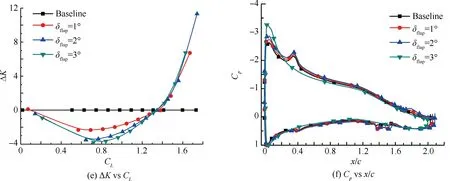
图25 后缘下偏角对气动特性的影响

Fig.25 Effect of trailing-edge flap angles on aerodynamic characteristics

前缘下偏6°的情况下，同时改变后缘下偏角，随着后缘襟翼向下偏转的角度增加，翼型的弯度和实际弦长得以增加，而参考弦长保持不变，因此获得了升力系数增量，而翼型弯度的增加同时导致了在各升力系数下低头力矩的增加。

从升力系数上看，前缘下偏6°使得翼型的失速特性有所改善，后缘襟翼下偏角越大，在失速之前能够获得的升力系数增量也越大，但是当迎角大于失速迎角后，后缘襟翼的下偏角度对升力系数增量影响不大。

当迎角在-4°～-1°之间时，相比于干净翼型，前缘下偏表现出了减阻的效果；当迎角在-1°～12°之间时，后缘襟翼下偏慢慢地表现出增阻效果；但是随着迎角增加，后缘襟翼下偏角对阻力的影响越来越明显，变弯构型又体现出了减阻效果，后缘下偏角越小，越早表现出减阻效果。

从升阻比曲线看，相比于干净翼型，当升力系数在0～1.37之间时，前后缘同时偏转导致了升阻比的损失，大约在升力系数为0.7时，升阻比损失最大，且后缘襟翼下偏角越大，升阻比损失越大；仅当升力系数大于1.37后，前后缘同时偏转获得了更高的升阻比。

4.2 固定后缘时前缘下偏角对气动性能的影响

选定δflap为2°，δdroop分别为3°、6°、9°、12°、15°，CFD计算的气动力结果如图26所示。

从升力系数上看，后缘襟翼下偏2°在各迎角下对升力系数贡献了一定的增量，导致升力系数曲线整体向上平移。在此基础上，通过前缘下偏改变翼型弯度在不同来流迎角下产生了不同效果，可以看到前缘下偏角越大，失速迎角越大，失速后升力系数曲线也更为缓和。相比于干净翼型，在迎角小于13°时，前缘下偏角越大，翼型的实际弯度越小，升力系数增量越小，而当迎角大于13°后则呈现出相反的规律。

同样的，对于阻力系数的影响也在不同迎角下有不同的规律，前缘下偏角越大，大迎角下越早产生减阻的效果。

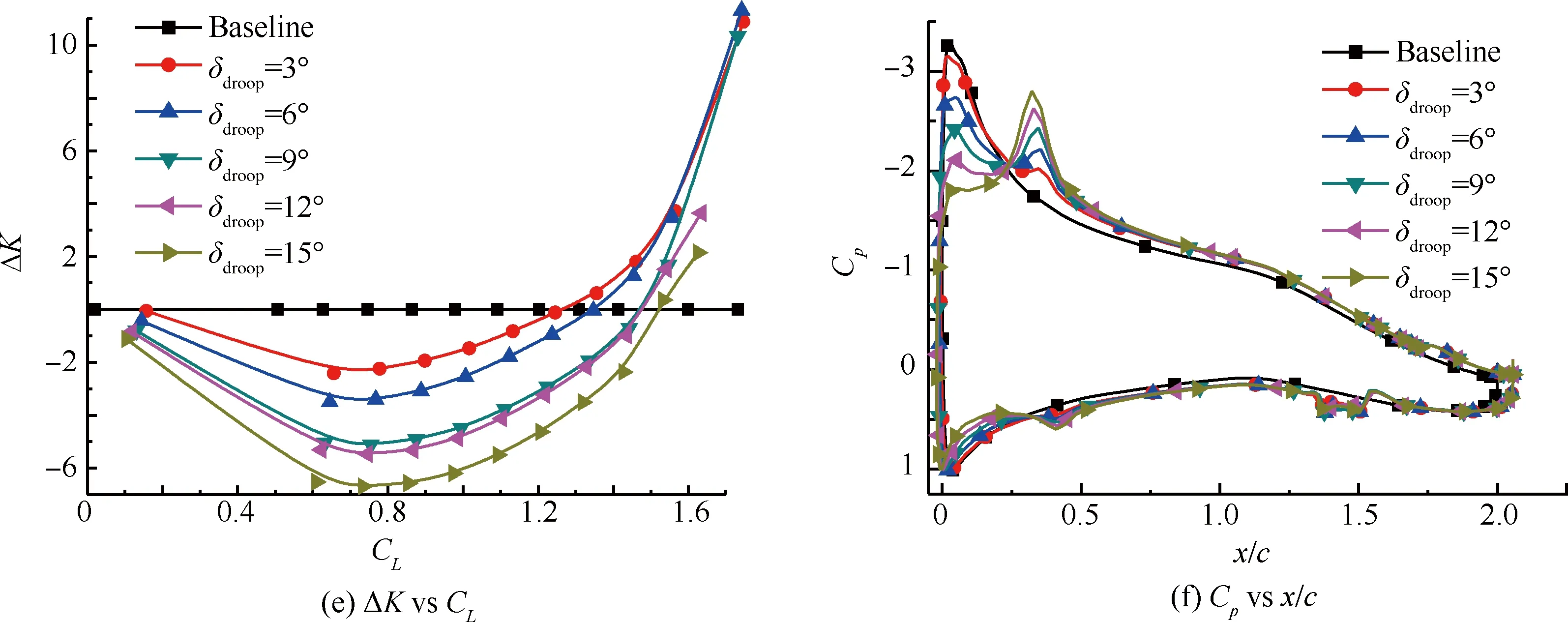
图26 前缘下偏角对气动特性的影响

Fig.26 Effect of leading-edge flap angles on aerodynamic characteristics

前缘下偏角对低头力矩的影响主要体现在失速之前，下偏角越大，低头力矩越大，但在失速后，前缘下偏对低头力矩几乎没有影响。

从升阻比曲线看，相比于干净翼型，不同的变弯构型仅在升力系数大于某一值时才产生更高的升阻比。在升力系数小于这个阈值时，前缘下偏角越大，升阻比的损失越大，其阈值也越大，因此要想在更大升力系数范围内获得更高的升阻比，前缘下偏角不宜过大。

5 结 论

1) 前缘下垂角改变了下垂位置上翼面负压峰值，从而使失速性能有所改善；同时吸力峰位置随着下垂弦长增加而后移，从而减缓失速，提高大迎角时的升力系数，增加失速迎角。

2) 后缘襟翼以及副翼偏转改变了翼型的有效弯度，前缘吸力峰值、上翼面负压值以及下翼面正压值均随着弯度的增加而增大。襟翼以及副翼下偏提高了翼型在失速前的升力系数及最大升力系数，但会稍微减小失速迎角。

3) 前后缘同时变弯度，在小迎角时，受到后缘下偏的影响较大，升力系数、阻力系数同时增加，升阻比减小；在大迎角时，受到前缘下垂的影响较大，升力系数继续大幅增加，失速迎角也增大。

4) 前缘下垂降低了前缘的吸力峰，后缘下偏则增加了后缘的升力，这都使得翼型低头力矩增加。

[1] NGUYEN N, PRECUP N, URNES J， SR, et al. Experimental investigation of a flexible wing with a variable camber continuous trailing edge flap design[C]//32nd AIAA Applied Aerodynamics Conference. Reston: AIAA, 2014.

[2] LEBOFSKY S, TING E, NGUYEN N. Aeroelastic modeling and drag optimization of aircraft wing with variable camber continuous trailing edge flap[C]//32nd AIAA Applied Aerodynamics Conference. Reston: AIAA, 2014.

[3] URNES J, SR, MORRIS C, SHEAHAN J, et al. Control system design for a variable camber continuous trailing edge flap system on an elastic wing[C]//55th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston: AIAA, 2014.

[4] URNES J， SR, NGUYEN N, IPPOLITO C, et al. A mission—Adaptive variable camber flap control system to optimize high lift and cruise lift-to-drag ratios of future N+3 transport aircraft[C]//51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Reston: AIAA, 2013.

[5] SINAPIUS M, MONNER H P, KINTSCHER M, et al. DLR’s morphing wing activities within the European network[J]. Procedia IUTAM, 2014, 10(1): 416-426.

[6] AHMED S, GUO S. Optimal design and analysis of a wing with morphing high lift devices[C]//54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston: AIAA, 2013.

[7] DI MATTEO N, GUO S, MORISHIMA R. Optimization of leading edge and flap with actuation system for a variable camber wing[C]//53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Reston: AIAA, 2012.

[8] DI MATTEO N, GUO S, LI D. Morphing trailing edge flap for high lift wing[C]//52nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Reston: AIAA, 2011.

[9] DI MATTEO N, GUO S, AHMED S, et al. Design and analysis of a morphing flap structure for high lift wing[C]//51st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston: AIAA, 2010.

[10] PERERA M, HE Y, GUO S. Structural and dynamic analysis of seamless aeroelastic wing[C]//51st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston: AIAA, 2010.

[11] PERERA M, GUO S. Optimal design of a seamless aeroelastic wing structure[C]//50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston: AIAA, 2009.

[12] MONNER H P, KINTSCHER M, LORKOWSKI T, et al. Design of a smart droop nose as leading edge high lift system for transportation aircrafts[C]//50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston: AIAA, 2009.

[13] LI D C, GUO S J, HE Y Y, et al. Nonlinear aeroelastic analysis of morphing flap[J]. International Journal of Bifurcation and Chaos, 2012, 22(5): 125009-125020.

[14] YOKOZEKI T, SUGIURA A. Development of variable camber morphing airfoil using corrugated structure[J]. Journal of Aircraft, 2014, 51(3): 1023-1029.

[15] YOKOZEKI T, SUGIURA A. Development and wind tunnel test of variable camber morphing wing[C]//22nd AIAA/ASME/AHS Adaptive Structures Conference. Reston: AIAA, 2014.

[16] 陈钱， 白鹏， 尹维龙, 等. 可连续光滑偏转后缘的变弯度翼型气动特性分析[J]. 空气动力学学报， 2010, 28(1)： 46-53. CHEN Q, BAI P, YIN W L, et al. Analysis on the aerodynamic characteristics of variable camber airfoils with continuous smooth morphing trailing edge[J]. Acta Aerodynamics Sinica, 2010, 28(1): 46-53 (in Chinese).

[17] 尹维龙. 关节式准柔性后缘翼型的气动特性分析[J]. 哈尔滨工业大学学报, 2010, 42(11)： 1758-1761. YIN W L. Aerodynamic characteristics of multi-sectional variable trailing-edge airfoil[J]. Journal of Harbin Institute of Technology, 2010, 42(11)： 1758-1761 (in Chinese).

[18] 韩占忠， 王敬， 兰小平. FLUENT流体工程仿真计算实例与应用[M]. 1版. 北京： 北京理工大学出版社， 2004: 21-22. HAN Z Z， WANG J， LAN X P. The case and application of FLUENT fluid engineering simulation[M]. 1st ed. Beijing： Beijing Institute of Technology Press, 2004: 21-22 (in Chinese).

[19] WENTZ W H, JR, SEETBARAM H C, FISCKO K A. Force and pressure tests of the GA(W)-1 airfoil with a 20% aileron and pressure tests with 30% Fowler flap： NASA CR-2833[R]. Washington, D.C.: NASA, 1977.

[20] WENTZ W H, JR, SEETBARAM H C, FISCKO K A. Pressure distribution for the GA(W)-2 airfoil with 20% aileron 25% slotted flap and 30% Fowler flap： NASA CR-2948[R]. Washington, D.C.: NASA, 1978.

陆维爽 女， 硕士研究生。主要研究方向： 计算流体力学。

Tel: 010-62314528

E-mail: lujiaww@163.com

田云 男， 博士， 讲师。主要研究方向： 计算流体力学、翼型及机翼设计。

Tel: 010-82316670

E-mail: aircraft@buaa.edu.cn

刘沛清 男， 博士， 教授， 博士生导师。主要研究方向： 实验空气动力学、机翼及增升装置设计。

Tel: 010-82318967

E-mail: lpq@buaa.edu.cn

王涛 男， 硕士研究生。主要研究方向： 计算流体力学。

E-mail: 273872093@qq.com

张良富 男， 硕士研究生。主要研究方向： 计算流体力学。

E-mail: 1053165986@qq.com

Received： 2015-03-17； Revised： 2015-05-18； Accepted： 2015-06-16； Published online： 2015-06-30 15:37

URL： www.cnki.net/kcms/detail/11.1929.V.20150630.1538.001.html

*Corresponding author. Tel.： 010-82318967 E-mail: lpq@buaa.edu.cn

Aerodynamic performance of GAW-1 airfoil leading-edge andtrailing-edge variable camber

LU Weishuang1, TIAN Yun1, LIU Peiqing2,*, WANG Tao1, ZHANG Liangfu1

1.LargeAircraftAdvancedTrainingCenter,BeihangUniversity,Beijing100083,China2.SchoolofAeronauticScienceandEngineering,BeihangUniversity,Beijing100083,China

The traditional high-lift device is used to improve the taking-off and landing aerodynamic performance of aircraft. By using the method of computational fluid dynamics (CFD), an idea of leading-edge and trailing-edge variable camber devices based on general aviation airfoil is introduced. The influences of leading-edge variable camber device, trailing-edge flap/aileron, and both leading-edge and trailing-edge variable camber devices of GAW-1 airfoil in the climbing state on airfoil aerodynamic performances are studied respectively. Learning from the results, leading-edge variable camber device can effectively improve the airfoil stall characteristics, increasing the angle of stall by about 3°, and the maximum lift coefficient has been increased by 4.56%. At the same time, the lift-to-drag ratio has been increased by 50% to 120%. But with the design lift coefficient, both lift coefficient and drag coefficient have been decreased. On the other hand, the function of trailing-edge variable camber device is to reposition the maximum of lift-to-drag ratio and to increase the lift coefficient by about 6% at a small angle of attack. Composite deflection of airfoil can increase lift coefficient at small angle of attack and increase lift-to-drag ratio at large angle of attack.

general aircraft; leading-edge droop nose; trailing-edge flap; ailerons; variable camber; aerodynamic performance

2015-03-17；退修日期：2015-05-18；录用日期：2015-06-16； < class="emphasis_bold">网络出版时间：

时间： 2015-06-30 15:37

www.cnki.net/kcms/detail/11.1929.V.20150630.1538.001.html

.Tel.： 010-82318967 E-mail: lpq@buaa.edu.cn

陆维爽， 田云， 刘沛清， 等. GAW-1翼型前后缘变弯度气动性能研究[J]. 航空学报， 2016, 37(2): 437-450. LU W S, TIAN Y, LIU P Q, et al. Aerodynamic performance of GAW-1 airfoil leading-edge and trailing-edge variable camber[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 437-450.

http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn

10.7527/S1000-6893.2015.0185

V211.4

： A

： 1000-6893(2016)02-0437-14

*