月球钻取采样机构的钻杆结构与运动参数分析

王丽丽, 刘志全, *, 吴伟仁, 张之敬

1. 北京理工大学 机械与车辆学院， 北京 100081 2. 中国空间技术研究院， 北京 100094 3. 探月与航天工程中心， 北京 100037

月球钻取采样机构的钻杆结构与运动参数分析

王丽丽1, 2, 刘志全1, 2, *, 吴伟仁1, 3, 张之敬1

1. 北京理工大学 机械与车辆学院， 北京 100081 2. 中国空间技术研究院， 北京 100094 3. 探月与航天工程中心， 北京 100037

针对月球钻取式自动采样机构空心外螺旋钻杆取样过程，分别建立了月壤内聚力和月壤内摩擦系数随月壤深度变化的数学模型，建立了钻进过程中钻杆运动参数(钻进速度和钻杆转速)与钻杆结构参数(钻杆螺旋升角、外径、槽宽比和螺旋槽深等)之间的关系。建模过程考虑了月壤物理和机械特性随钻进深度变化特性、钻杆钻进牵连速度及月壤微元相互间的抗剪性，使得钻杆参数符合月球钻取采样的实际工况。对模型进行了验证，利用该模型开展了钻杆结构参数对运动参数的影响分析，给出了钻杆结构参数对钻杆运动参数的影响规律，获得了钻杆结构参数的最佳取值范围。以钻杆转速与钻进速度比最小为优化目标，以结构参数为设计变量，基于遗传算法对钻杆结构参数进行了优化，优化后的钻杆转速与转进速度比降低了13.8%。该优化结果降低了系统能耗，提高了钻取采样输月壤效率，可为钻取式自动采样机构的设计提供理论依据。

钻取采样机构； 空心外螺旋钻杆； 结构参数； 运动参数； 月壤； 采样

在月球、火星乃至未来其他星球的深空探测任务中，星球表面或表下土壤及岩石样品的采集对于研究星球环境、地质构造、资源以及物质组成等具有重要意义[1]。钻取式自动采样机构相比其他采样机构，因能够保持所采样品的层理特性而备受关注。空心外螺旋钻杆作为常用的一种钻杆[2]，是钻取式自动采样机构实现快速优质钻进的重要部件，用以传递钻机动力、承受轴向力和回转扭矩。钻杆的运动参数(转速和钻进速度)影响着整个采样机构的取样效率，若运动参数选择不合理，会带来堵钻和烧钻等风险，因此对钻杆结构与运动参数的分析是设计钻取式采样机构的关键之一。

国外对星球采样的螺旋钻杆结构详细设计与分析至今未见公开报道。国内文献[2]建立了月壤与钻杆作用力的数学模型，但未考虑月壤微元块相互间的抗剪性、钻杆提供给月壤的钻进牵连速度及月壤随钻进深度动态特性变化。文献[3]虽考虑了钻杆提供给月壤的钻进牵连速度，但忽略了月壤微元块间的抗剪性,也未对模型进行验证及参数优化。文献[4]以钻杆输出月壤所消耗的功率最小为目标，对钻杆结构参数进行了优化设计，但所建立的阻力矩模型仅适用于钻杆螺旋升角小于5°的情况，而不适用于钻杆螺旋升角较大(10°～20°)的情况，也未对钻杆运动参数进行分析，而是直接采用定值。文献[5]涉及的空心外螺旋钻杆结构虽然与月面钻取式自动采样机构的钻杆结构相似，但文献[5]是基于地球土壤特性进行分析的，而月壤与地球土壤的力学特性不同，若按地球土壤特性设计钻杆，难以适应月球采样。文献[6-7]虽然涉及了月壤钻取采样，但研究对象并非钻杆而是钻头。

基于上述背景，本文在综合考虑月壤物理和机械特性随钻进深度变化特性、钻杆钻进牵连速度及月壤微元块相互间抗剪性的基础上，分别建立月壤内聚力和月壤内摩擦系数随月壤深度变化的数学模型，建立钻进过程中钻杆运动参数(钻进速度和钻杆转速)与钻杆结构参数(钻杆螺旋升角、外径、槽宽比和螺旋槽深等)之间的关系，验证模型的有效性。借助这些模型，开展钻杆结构参数对钻杆运动参数的影响分析，获取钻杆结构参数的最佳取值范围，以钻杆转速与钻进速度比最小为目标，基于遗传算法对钻杆结构参数进行优化，为钻取式自动采样机构的设计提供理论依据。

1 钻取式采样机构的工作原理及月壤特性

图1展示了苏联Luna-24月球探测器钻取式自动采样机构的工作原理[8-9]。采样时，钻机和传送机构同时工作，钻杆在周向回转驱动力矩和轴向加载力的共同作用下钻入月壤。钻杆横截面为双层同心圆结构，其内层钻杆的内壁上装有专门的柔性取样袋。随着钻探深度增大，月壤逐渐进入内层钻杆的空腔内，柱形月壤被柔性取样袋收集其中。柔性取样袋顶端封闭并与钢丝绳连接，钢丝绳沿着支撑桁架向上缠绕在回收机构的卷筒上。当钻杆钻入指定深度后，柔性取样袋下端封住所取样品。安装于支撑桁架顶端的回收机构通过电机驱动回收卷筒和缠绕钢丝绳将内层钻杆中的柔性取样袋提出并缠绕至回收卷筒上。回收机构中装有释放分离装置，将缠绕了柔性取样袋的卷筒弹入返回器内。最后，火工装置起爆断开支撑桁架与传送机构之间的连接[10]。

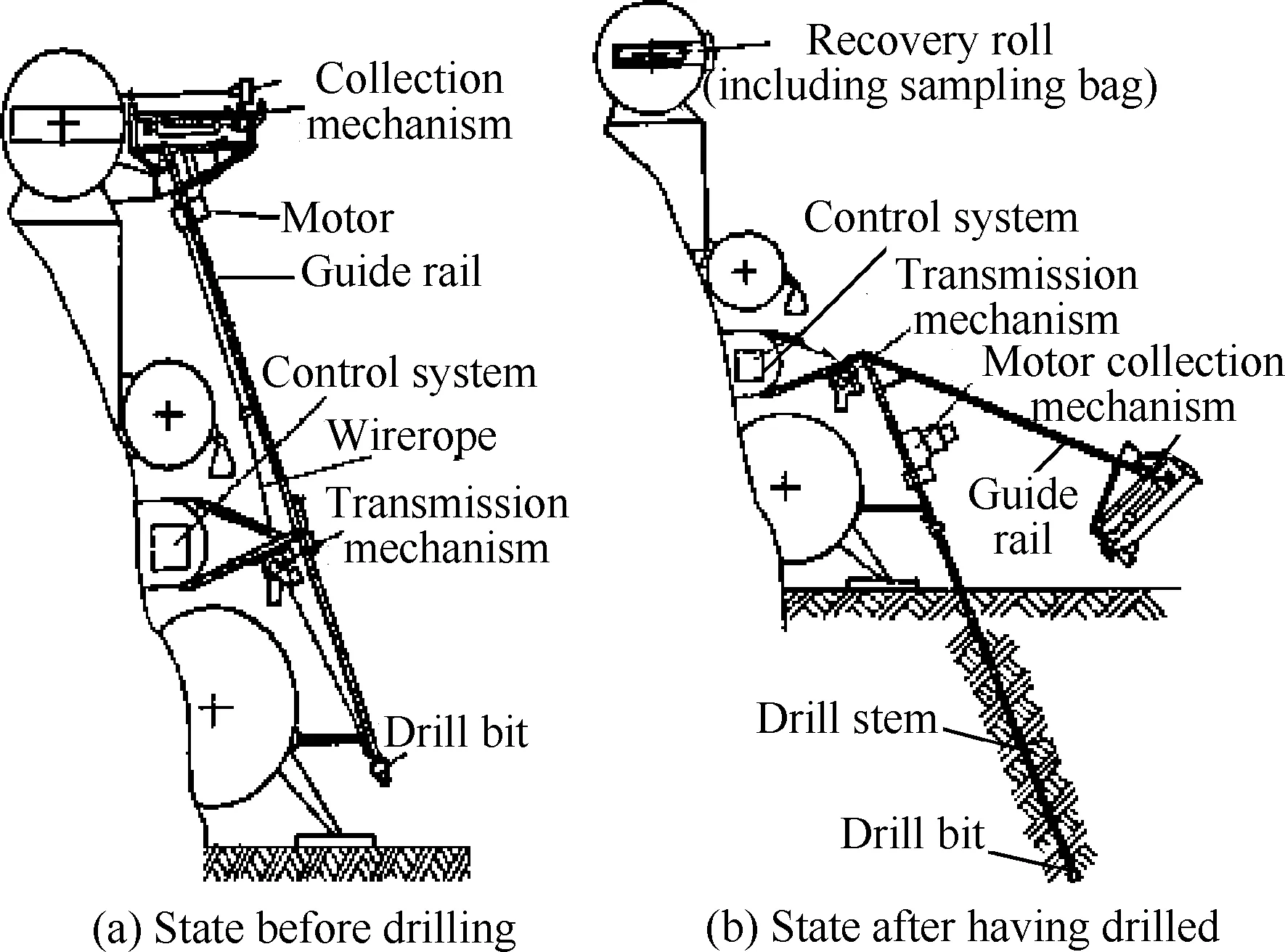
图1 Luna-24月球探测器上的钻取式自动采样机构[8-9]

Fig.1 Automatic drilling sampling mechanism on Luna-24 explorer[8-9]

月壤是由固体颗粒组成的，颗粒间的连结强度远远小于颗粒本身的强度,故在外力作用下颗粒之间发生相互错动[11-13]。月表分布面积最广的地貌为相对平缓的均一地貌，该地区月壤的孔隙比约为0.8～1.0，更松散的月壤大多出现在具有较大坡度的地貌区。由月表月壤的孔隙比与承载力的对应关系[9]可知，相对平缓和撞击坑交叠区，月表月壤的承载力为25～55 kPa的概率最大。月表月壤较为松散，承载力不高[14]，钻取式自动采样机构不需要较大钻压力即可钻入；而随着月壤深度的增加，月壤的容重、内摩擦角增大，孔隙比减小，月壤的压实程度增加。月壤颗粒形态多样，长条状、次棱角状和棱角状的颗粒形态较为常见，棱角状(特别是锯齿状)粒形使得月壤颗粒之间互锁，相互滑行困难，这导致次月表月壤在抵抗外物锲入方面几乎类似于固体岩石，岩芯取样器需要更大的压力才能顺利取样。因此研究月壤微元块运动分析时，可把钻杆螺旋面之间的月壤看成由n个正方体微元块颗粒组成。研究其相互错位时，需考虑月壤微元块所受的剪切力，还需考虑月壤密度、摩擦系数及内聚力随着钻进深度的变化关系。

2 空心螺旋钻杆与月壤相互作用力学模型

2.1 基本假设

根据钻取式采样机构在月面钻取月壤的特点，为简化计算作如下假设：①钻杆的几何尺寸、钻杆材料的机械性能在钻进过程中保持不变，不考虑温升对钻杆运行状态的影响；②钻杆横截面刚性且与中心线正交，材料各向同性；③螺旋槽内月壤被考虑为连续粘结体，前后方月壤对微元块压力等大且n个月壤微元块相对螺旋面具有相同的螺旋向上运动和角速度。

2.2 月壤微元块运动参数的解析模型

钻杆在钻进月壤过程中，螺旋钻杆以角速度ω回转时，月壤微元块相对于螺旋叶片滑动。设钻杆一个螺距内有n个刚体正方体微元块自然堆积。月壤微元块的受力如图2所示，空心外螺旋钻杆结构如图3所示。

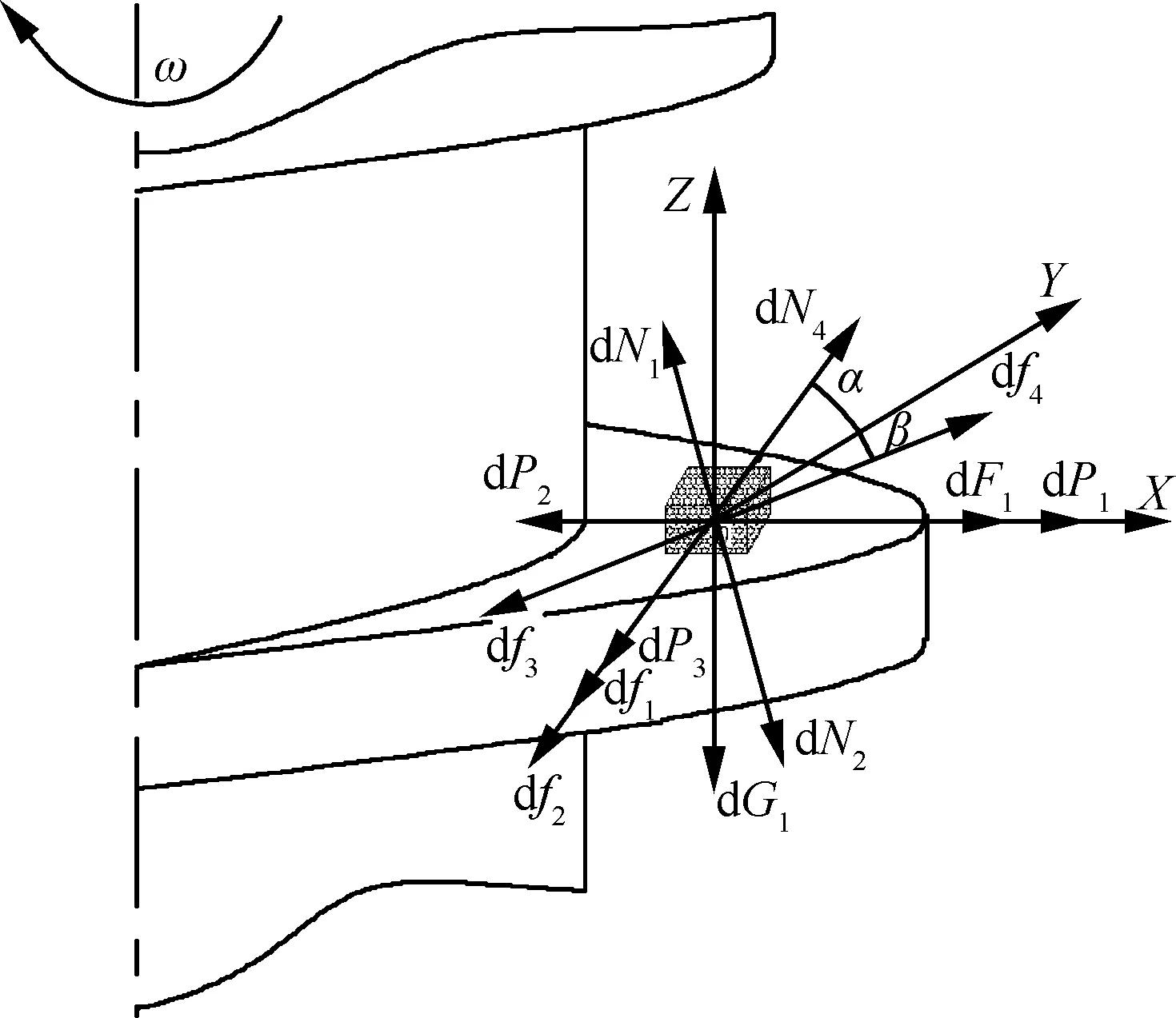
图2 月壤微元块受力图

Fig. 2 Force diagram of lunar-soil infinitesimal

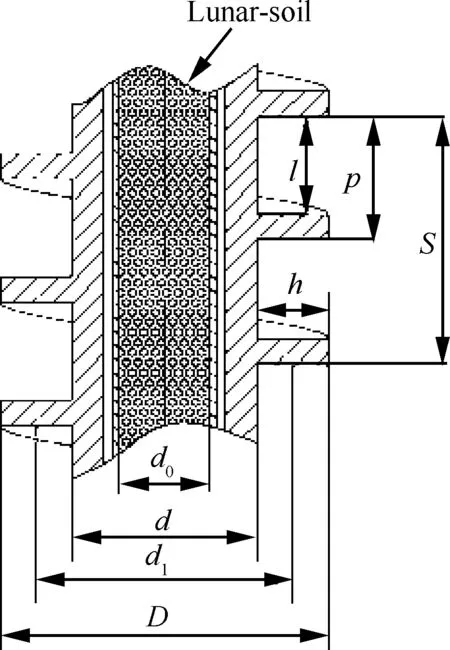
图3 空心外螺旋钻杆结构

Fig. 3 Structure of hollow-external-screw drill stem

在图2中，XYZ为三维直角坐标系，X为径向，Y为切向(周向)，Z为轴向；α为钻杆的螺旋升角；β为月壤微元块的螺旋升角；dF1为微元块在螺旋槽中运动的离心力；dG1为微元块的重力；dN1、df1分别为螺旋叶片对月壤微元块的支持力和摩擦力；dN2、df2分别为上方月壤对微元块的压力和剪切力；dP1、df3分别为左方月壤对微元块的压力和剪切力；dP2、df4分别为右方月壤对微元块的压力和剪切力；dP3、dP4分别为前方和后方月壤对微元块的压力，dP3和dP4等大反向。

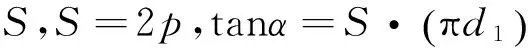
(1)

当β=0°时，微元块处于极限平衡状态，即微元块保持在同一水平高度做圆周运动，既不上升也不下滑，此时dP2≤dF1，dP1和df2不存在，存在临界深度z0，使得dP2=dF1，通过平衡方程式(1)，可获得钻杆排出月壤的临界角速度ω0。

当β>0°时，进一步增大钻杆的回转角速度，dF1逐渐增大，则左、右方微元块的df3和df4分别增大，此时dP2>dF1，dP1和df2存在，由于微元块受到了相对水平面向上运动的力，因此微元块可从钻孔底部排出。此时微元块的运动过程，可认为是微元块相对水平面向上的运动和随螺旋钻杆回转运动的复合，最终微元块以β向上螺旋匀速转动。df1、df2、df3和df4的表达式为

(2)

(3)

紧贴图2所示微元块上方的微元块(第2个月壤微元块)的受力如图4所示。

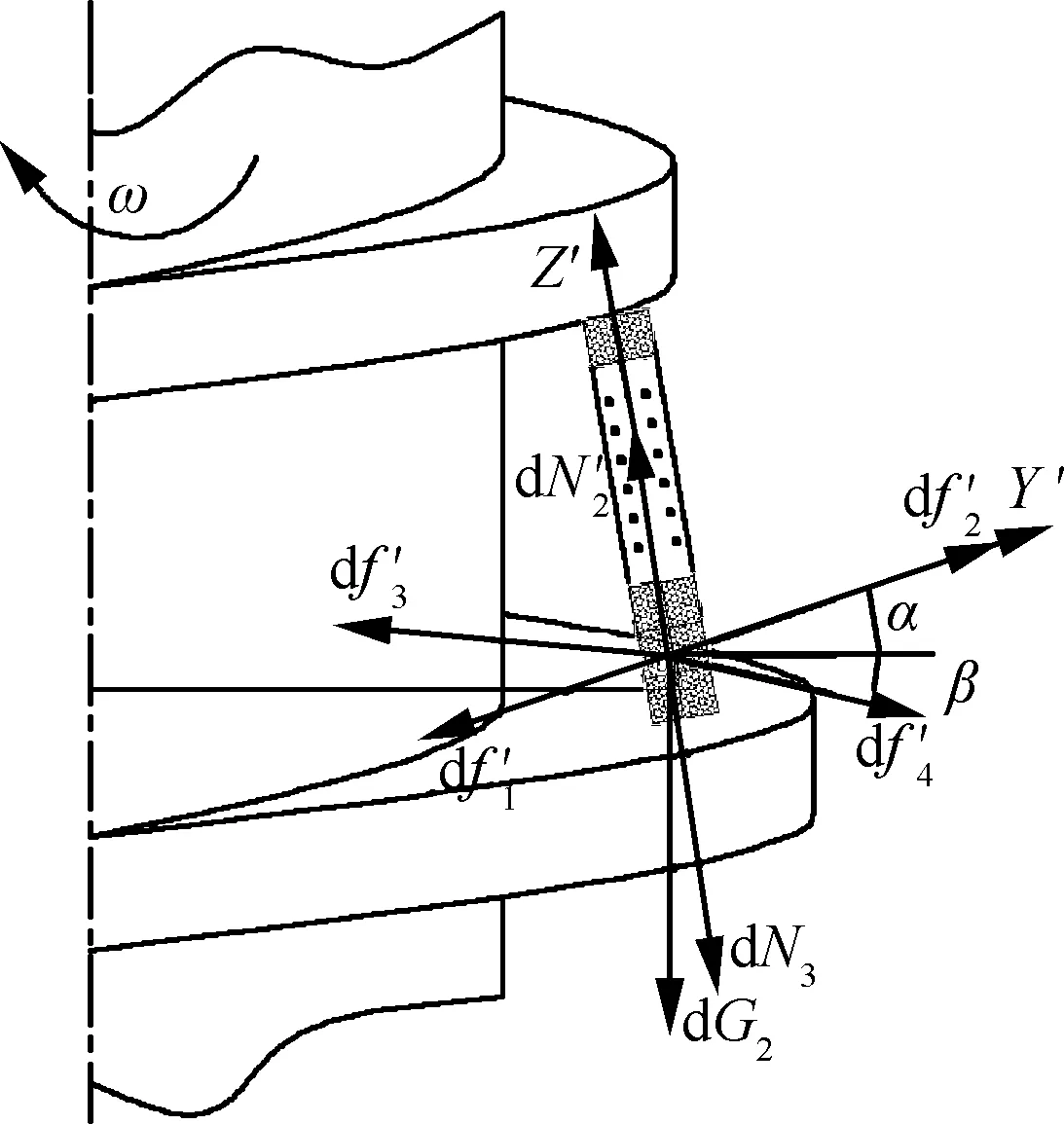
图4 正压力方向上的一个小微元块受力图

Fig. 4 Force diagram of a lunar-soil infinitesimal in positive pressure direction

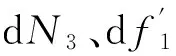
(4)

据式(3)和式(4)，同理可得在Z′方向上的n-1 个微元块力平衡方程，则有

(5)

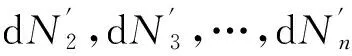
根据式(5)，得

由式(1)及N1、N2可求得

(7)

把β=0°代入式(7)中，便可得微元块的临界角速度ω0，根据dP2=dF1，则有

(8)

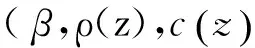
2.3 钻杆运动参数与月壤微元绝对角速度的关系

当钻取机构实际转速为nz时，螺旋槽内月壤在随钻取机构旋转的同时，还相对螺旋面向上滑动，实现钻屑的有效排出。槽内微元块的绝对运动也为螺旋运动，其旋向与钻杆螺旋面的旋向相反，与水平方向的夹角为β，微元块在螺旋叶片上的绝对速度va由钻杆回转牵连速度vp、钻杆钻进牵连速度vj和槽内月壤微元相对螺旋面的滑行速度vr合成，即va=vp+vj+vr，如图5所示，可分解为垂直向上的速度vt和水平周向速度vh，则有钻头单位时间内切削月壤的体积SD等于单位时间内通过空心螺旋内钻杆体积Sd与单位时间内通过螺旋槽垂直截面月壤的体积Sk的和，即

(9)

图5 月壤微元运动分析

Fig. 5 Kinematic analysis of lunar-soil infinitesimal

SDvj=Sk(vt+vj)+Sdvj

(10)

式中：SD=π(0.5D)2；Sd=π(0.5d0)2；Sk=ψπφ-1((0.5D)2-(0.5d)2)=0.25ψφ-1π(D2-d2)，其中φ为螺旋槽内月壤的松散体积系数，取φ=1.6[3]。

由式(10)可得螺旋钻杆钻进速度v(即vj)

(11)

式(11)为钻进过程中v与ωs的关系式。

把式(9)和式(10)代入式(11)，整理可得螺旋钻杆转速为

(12)

式(12)即钻进过程中nz与ωs的关系式，可见v和nz都与钻杆结构参数、钻杆月壤间摩擦系数、月壤螺旋升角、月壤特性相关。

3 月壤内聚力、月壤内摩擦系数随月壤深度的变化

美国的Mitchell院士利用地面玄武岩配制了不同孔隙比e的模拟月壤[15]，通过数据拟合给出了式(13)所示的线性关系:

tanφ=1.377 9e-1-0.392 5

(13)

(14)

(15)

月壤与钛合金钻杆的摩擦系数暂无文献报道，根据月壤物理特性并考虑到月壤属于不饱和粘土，该摩擦系数近似按模拟月壤与钛合金的摩擦系数试验值选取μ1=0.35[3]。

4 试验验证

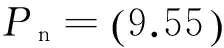
为了验证式(11)和式(12)的正确性，用某钻取式自动采样机构的试验数据与理论数据进行比对，将试验参数及μ1=0.35代入理论模型式(12)中，得到D与nz的关系曲线如图6所示。

由图6可见，理论曲线与试验曲线变化趋势基本吻合，二者最大相对误差(理论值与试验值差的绝对值除以理论值)为8.62%，验证了所建模型的正确性。理论与试验数据之间的误差主要来源于二者之间所用模拟月壤特性的差异。

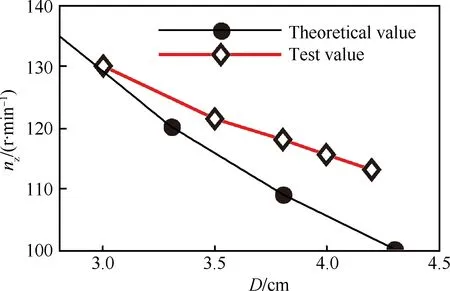
图6 试验数据与理论数据对比

Fig. 6 Comparison between test value and theoretical value

5 钻杆结构参数对运动参数的影响分析

在u0=10/13,D=3.5 cm,h=0.4 cm的情况下结构参数α和β对运动参数的影响如图7所示。

由图7(a)可见，在β=0°～10°，α=0°～20°时，v随α变化近似成线性关系，但斜率很小，v的变化很小，当α=20°～30°时，v和α成非线性关系，随着α增大而急剧增大，β的影响较为明显。由图7(b)可见，nz-α曲线存在极小值，nz的极小值分别发生在α=9°,β=5°；α=11.5°,β=8°；α=12.5°,β=10°时；在相同α值下，β越大，nz越大，由此可推断出为了减小钻杆能耗，尽可能使nz取极小值，β尽可能小。由图7(c)和图7(d)可见，在α一定的情况下，v和nz随β的增大而增大，由图7(d)可见，当β增大到一特定值时，v和nz变为0，即发生停钻(Luna-20曾发生过停钻现象)，α越大，发生停钻的β值越小，α越小，发生停钻前β值的可取范围更大，则较小的α和较小的β组合，可使得nz较小，达到降低功耗效果。可见α对钻杆运动特性影响较大，须对α取值加以控制，只有当α小于arctanμ1时，微元块间的相互作用力与月壤屑运动方向相同，才成为驱动力，使月壤屑匀速运动，因此α≤arctanμ1=19.29°，综合以上分析，α在9°～19°区间选择最有利。

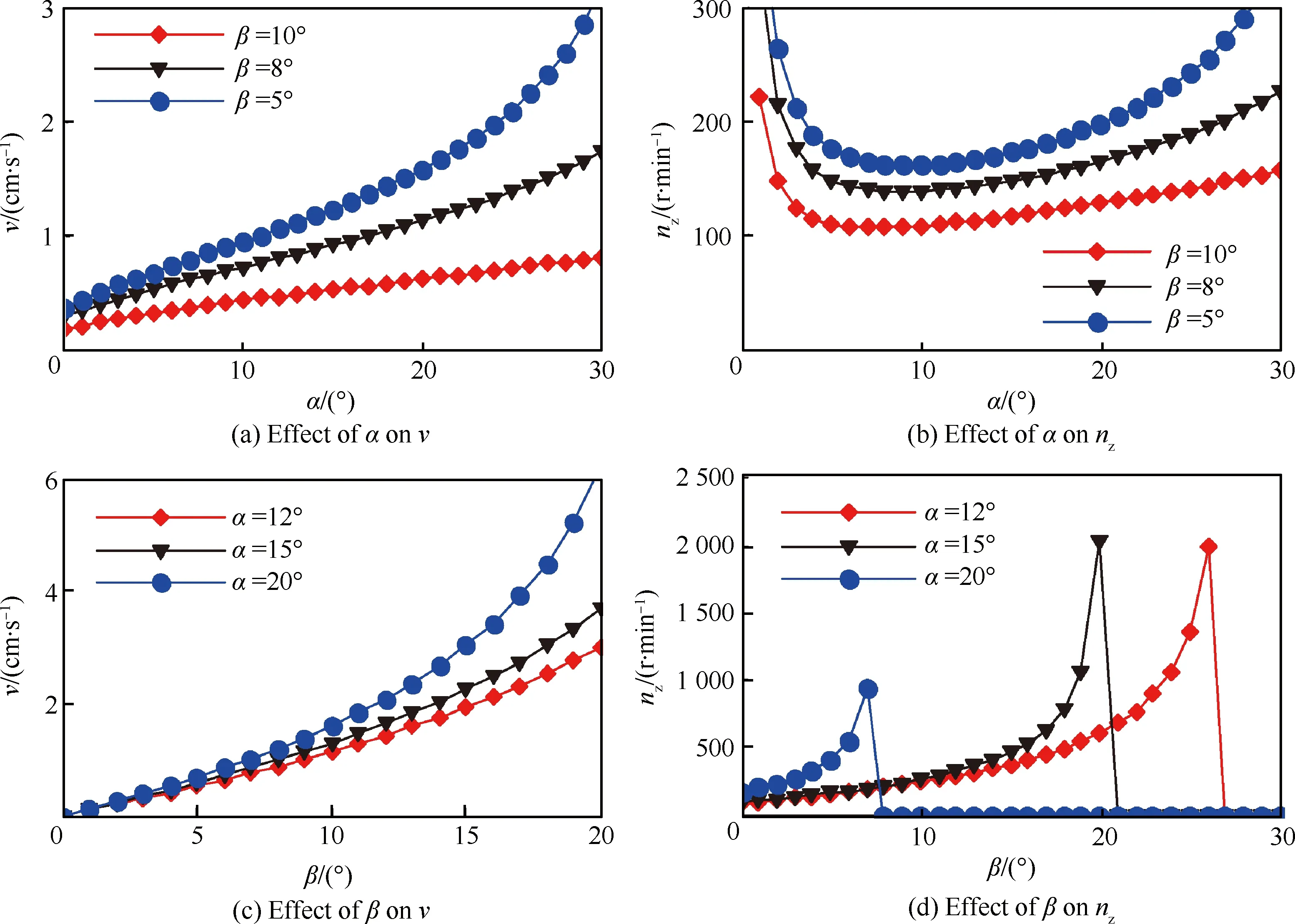
图7 螺旋升角对钻杆运动参数的影响

Fig. 7 Effect of spiral angle on drill stem kinematic parameters

在α=15°,D=3.5 cm,h=0.4 cm的情况下结构参数u0对运动参数的影响如图8所示。

图8 槽宽比对钻杆运动参数的影响

Fig. 8 Effect of groove width ratio on drill stem kinematic parameters

由图8可见，v和nz均与u0成正比，随u0的增大而线性增大，而u0的增大意味着螺旋槽内月壤容量增加，在钻杆扭转功率和钻进功率一定的情况下，u0的增大有利于减小钻进压力和钻杆扭矩，有利于增大输月壤量及其效率，反之u0过小，容易造成月壤排屑不畅和钻杆堵钻。因此在满足钻杆结构强度裕度的前提下，尽可能取较大的u0值(在u0的取值范围(u0<1)内)，可提高月壤排屑的流畅性，建议u0的取值范围为0.7～0.9。

在α=15°,u0=10/13,h=0.4 cm的情况下结构参数D对运动参数的影响如图9所示。

图9 外径对钻杆运动参数的影响

Fig. 9 Effect of outer diameter on drill stem kinematic parameters

由图9可见，v和nz分别与D成负相关，且在D=3.4cm之后变化趋于平缓，由图9(a)所示，D越小v越高，钻取采样输月壤效率越高。由图9(b)可知适当增加D可降低排屑时对nz的要求，从而减少系统能耗，但当D继续增大时钻杆与月壤摩擦面积增大，则钻杆的输月壤功率呈增大趋势，因此D的增大不利于轴向钻进和提高v，且运输功耗相对提高，因此D的取值范围为3.4～4.0cm。

在α=15°,u0=10/13,D=3.5 cm的情况下结构参数h对运动参数的影响如图10所示。

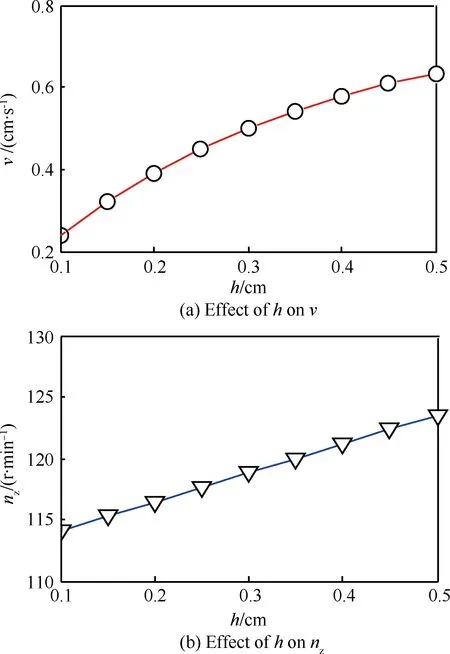
图10 螺旋槽深对钻杆运动参数的影响

Fig. 10 Effect of Spiral groove depth on drill stem kinematic parameters

由图10可见，v和nz分别与h成正相关，且h对v的影响幅度较大，由图10(a)可知，v在h=0.4 cm之后变化趋于平缓，h越大d越小，d的首要任务是完成钻压力及旋转扭矩的传递，在刚度和强度要求得到满足时，适当增加h可提高排屑的通畅性；由图10(b)可知h的减小可降低排屑时对nz的要求，从而减少系统能耗。基于钻孔空间、系统能耗、钻杆内径强度和刚度的限制，由于钻采孔径较小，根据经验值，h的取值范围为0.1D～0.15D。

由以上分析可知，若想降低系统能耗，提高钻取采样输月壤效率，则nz/v比值越小越好，因此以nz/v为优化目标，对钻杆结构参数进行优化。

6 钻杆结构参数优化

本文作者曾以钻杆总功耗等为优化目标，对钻杆结构参数进行了多目标优化[21]，此处不再赘述。本文以nz/v最小为优化目标，开展钻杆结构参数优化。

设计变量为X={D,u0,α,h}，目标函数为

(16)

由图11可见，在迭代53次后收敛，nz/v最佳值为214.180。钻杆结构参数的优化结果见表1。

由表1可见，优化后的nz/v降低了13.8%。可按表1的优化结果选取钻杆结构参数。

图11 遗传算法优化图

Fig. 11 Optimization by genetic algorithm

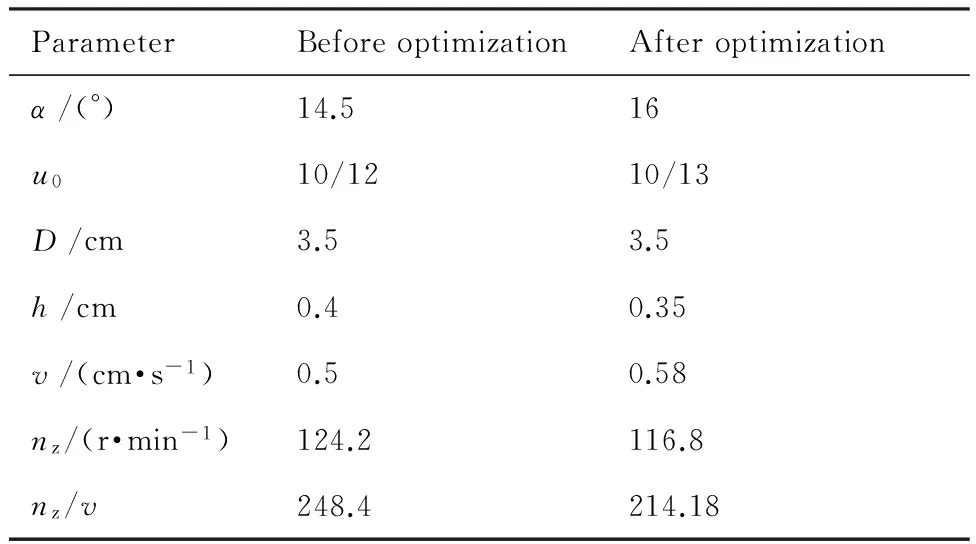
表1 优化前后钻杆结构参数的对比

Note: * Trial value is from some type automatic drilling sampling mechanism.

7 结 论

1) 在综合考虑了月壤物理和机械特性随钻进深度变化关系、钻杆钻进牵连速度及月壤微元相互间的抗剪性的情况下，所建立的钻杆结构参数与钻杆运动参数之间的模型符合月球钻取采样的工作要求，钻杆运动参数的理论值与试验值之间误差为8.62%，验证了所建模型的正确性。

2) 基于本文某钻取机构的运动参数，可选择表1给出的钻杆结构优化参数。

3) 钻杆螺旋叶片升角α在9°～19°区间，月壤块螺旋升角β为5°时，钻杆提供较小的回转速度即可实现孔底钻屑的排出，此时系统能耗小、稳定性好。

4) 钻杆钻进速度v和转速nz分别与槽宽比u0成正比关系，在功率允许的条件下，适当的增加u0，可提高月壤排屑的流畅性，u0的取值范围为0.7～0.9。

5) 钻杆钻进速度v和转速nz分别与外径D呈负相关，且在D=3.4cm之后变化趋于平缓，D越小钻取采样输月壤量效率越高，要尽量减小D。而适当增加D可以降低排屑时对钻杆回转速度的要求，从而减少系统能耗，D的取值范围为3.4～4.0cm。

6) 钻杆钻进速度v和转速nz分别与螺旋槽深h成正相关，在刚度和强度要求得到满足时，适当增加h可提高排屑的通畅性；h的减小可降低排屑时对nz的要求，从而减少系统能耗。根据经验值，h的取值范围为0.1D～0.15D。

[1] 吴伟仁, 周健亮, 高薇, 等. 绕月探测卫星飞行控制[M]. 北京: 中国宇航出版社, 2012: 5-20. WU W R, ZHOU J L, GAO W, et al. Lunar exploration satellite flight control[M]. Beijing: China Astronautic Publishing House, 2012: 5-20 (in Chinese).

[2] 庞彧, 刘志全, 李新立. 月面钻取式自动采样机构的设计与分析[J]. 中国空间科学技术, 2012, 32(6): 16-23. PANG Y, LIU Z Q, LI X L. Design and analysis of automatic drilling sampling mechanism for lunar exploration[J]. Chinese Space Science and Technology, 2012, 32(6): 16-23 (in Chinese).

[3] 刘飞, 侯绪研, 全齐全, 等. 空心外螺旋钻杆与月壤相互作用力学模型研究[J]. 机械制造, 2011, 49(567): 29-31. LIU F, HOU X Y, QUAN Q Q, et al. Study on the interaction mechanical model between hollow-external-screw drill rod and Lunar-soil[J]. Machinery, 2011, 49(567)： 29-31 (in Chinese).

[4] 田野, 邓宗全, 唐德威, 等. 月壤钻探采样装置中的钻杆结构参数优化设计及模拟试验[J]. 机械工程学报, 2012, 48(23): 10-14. TIAN Y, DENG Z Q, TANG D W, et al. Structure parameters optimization and simulation experiment of auger in Lunar-soil drill-sampling device[J]. Journal of Mechanical Engineering, 2012, 48(23): 10-14 (in Chinese).

[5] 赵伟民, 顾迪民, 牛红, 等. 螺旋钻具上的土的运动分析[J]. 哈尔滨建筑大学学报, 1999, 32(2): 71-73. ZHAO W M, GU D M, NIU H, et al. Motion analyses of the soil on the earth auger[J]. Journal of Harbin University of Civil Engineering and Architecture, 1999, 32(2): 71-73 (in Chinese).

[6] 李大佛, 雷艳, 许少宁. 月球钻探取心特种钻头研制与试验[J]. 探矿工程 (岩土钻掘工程), 2013, 40(2): 1-6. LI D F, LEI Y, XU S N. Study on particular coring bit for Lunar-soil drilling[J]. Exploration Engineering (Rock & Soil Drilling and Tunneling), 2013, 40(2): 1-6 (in Chinese).

[7] 邓宗全， 田野， 唐德威, 等. 用于地外星体探测的一种新结构取心钻头研究[J]. 机械工程学报, 2013, 49(19): 104-110. DENG Z Q, TIAN Y, TANG D W, et al. Reseach on new structure coring bit for extraterrestrial bodies exploration[J]. Journal of Mechanical Engineering, 2013, 49(19): 104-110 (in Chinese).

[8] ROBERT C. The mission of Luna 24 [EB/OL]. (1998-02-12)[2010-05-6]. http://www.zarya.info/Diaries/ Luna/Luna24.php.

[9] ROBERT C. The mission of Luna 16[EB/OL]. (1998-02-12)[2010-05-26]. http://www.zarya.info/Diaries/ Luna/Luna16.php.

[10] 刘志全, 庞彧, 李新立. 深空探测自动采样机构的特点及应用[J]. 航天器工程, 2011, 20(3): 120-125. LIU Z Q, PANG Y, LI X L. Characteristic and application of automatic sampling mechanisms for deep space exploration[J]. Spacecraft Engineering, 2011, 20(3): 120-125 (in Chinese)．

[11] 邹猛, 李建桥, 何铃, 等. 不同粒径分布模拟月壤承压特性试验研究[J]. 航空学报, 2012, 33(12): 2338-2346. ZOU M, LI J Q, HE L, et al. Experimental study on the pressure-sinkage characteristic of the stimulant lunar regolith with different particle size distributions[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(12): 2338-2346 (in Chinese).

[12] 郑永春, 欧阳自远, 王世杰, 等. 月壤的物理和机械性质[J]. 矿物岩石, 2004, 24(4): 14-19. ZHENG Y C，OUYANG Z Y, WANG S J, et al. Physical and mechanical properties of lunar regolith[J]. Journal of Mineralogy and Petrology, 2004, 24(4): 14-19 (in Chinese).

[13] 邓宗全, 丁亮, 高海波, 等. 月壤特性对月球车轮地相互作用力的影响[J]. 哈尔滨工业大学学报, 2010, 42(11): 1724-1729. DENG Z Q, DING L, GAO H B, et al. Influence of soil properties on lunar rover’s wheel-soil interaction mechanics[J]. Journal of Harbin Institute of Technology, 2010, 42(11): 1724-1729 (in Chinese).

[14] 金大玮, 李建桥, 党兆龙, 等. 滑转条件下月球车轮沉陷模型研究[J]. 航空学报, 2013, 34(5): 1215-1221. JIN D W, LI J Q, DANG Z L, et al. Study on model for sinkage of lunar rover wheel under slip[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(5): 1215-1221 (in Chinese).

[15] MITCHELL J M. Mechanical properties of lunar soil: Density, porosity, cohesion, and angle of interal friction[C]//Proceedings of the Third Lunar Science Conference. Houston, Texas: Lunar Science Institute and NASA, 1972(3): 3235-3253.

[16] 丁希仑, 李可佳, 尹忠旺. 面向月壤采集的多杆深层采样器[J]. 宇航学报, 2009, 30(3): 1189-1194. DING X L, LI K J, YIN Z W. Multi rod deep driller for lunar subsurface sampling[J]. Journal of Astronautic, 2009, 30(3): 1189-1194 (in Chinese).

[17] 褚桂柏, 张熇. 月球探测器技术[M]. 北京: 中国科学技术出版社, 2007: 59-60. CHU G B, ZHANG H. Lunar exploration technology[M]. Beijing: China Science and Technology Press, 2007: 59-60 (in Chinese).

[18] ORAVEC H A, ZENG X, ASNANI V M. Design and characterization of GRC-1: A soil for lunar terramechanics testing in Earth-ambient conditions[J]. Journal of Terramechics, 2010, 47(6): 361-377.

[19] JANOSI Z, HANAMOTO B. Analytical determination of drawbar pull as a function of slip for tracked vehicle in deformable soils[C]//Proceedings of 1st International Conference of ISTVS. Torino: International Society for Terrain-Vehicle Systems, 1961: 707-726.

[20] HEIKEN G, VANIMAN D, FRENCH B, Lunar sourcebook—a user’s guide to the moon[M]. New York: Cambridge University Press, 1991: 522-530.

[21] 王丽丽, 刘志全, 吴伟仁, 等. 月球钻取式自动采样机构螺旋钻杆结构参数的多目标优化[J]. 宇航学报, 2015， 36(6): 723-730. WANG L L, LIU Z Q, WU W R, et al. Multi-objective optimization to drill stem structural parameters of lunar automatic drilling sampling mechanism[J]. Journal of Astronautics, 2015， 36(6): 723-730.

王丽丽 女， 博士研究生， 主要研究方向： 航天器结构与机构技术。

E-mail: liliwang5188@163.com

刘志全 男， 博士， 研究员， 博士生导师， 中国航天科技集团公司学术技术带头人。主要研究方向： 航天器结构与机构技术、可靠性技术。

Tel.: 010-68747342

E-mail: liuzhiquanymj@sina.com

Received： 2015-01-07； Revised： 2015-01-26； Accepted： 2015-03-12； Published online： 2015-03-30 15:00

URL： www.cnki.net/kcms/detail/11.1929.V.20150330.1500.002.html

Foundation item： National Key Project of Science and Technology (TY3Q2011xxx01)

*Corresponding author. Tel.： 010-68747342 E-mail: liuzhiquanymj@sina.com

Analysis of drill stem structural and kinematic parameters of lunar drilling sampling mechanism

WANG Lili1, 2, LIU Zhiquan1, 2, *, WU Weiren1, 3, ZHANG Zhijing1

1.MechanicalandVehicularEngineeringCollege,BeijingInstituteofTechnology,Beijing100081,China2.ChinaAcademyofSpaceTechnology,Beijing100094,China3.LunarExplorationandAerospaceEngineeringCenter,Beijing100037,China

In respect of the sampling process of the hollow-external-screw drill stem for automatic drilling sampling mechanism, the mathematical models between the cohesive force, friction coefficient of lunar-soil and the lunar-soil depth are built separately; the relationships between drill stem kinematic parameters (drill stem drilling speed and rotary speed) and the structural parameters (drill stem spiral angle, outside diameter, groove width ratio and spiral grooved depth in the drilling process) are also established. These models take into account not only the characteristics of lunar-soil physical and mechanical parameters changing with drilling depth and drill stem drilling convected velocity, but also the shear resistance among lunar-soil infinitesimals. Such approach subjects the drill stem’s parameters to the job requirement of lunar drilling sampling. The effectiveness of the model is validated and the analysis of the influence of the drill stem structural parameters on its kinematic parameters is conducted with the models. As a result, the influence law of the drill stem structure parameters on its kinematic parameters is revealed, and the best value range of drill stem structure parameters is obtained. Taking the minimum value of the ratio between the drill stem rotary speed and drilling speed as optimal object and the structural parameters as design variables, based on genetic algorithm, the structural parameters of drill stem are optimized. Before and after optimization, the ratio of drill stem rotary speed to drilling speed is reduced by 13.8%. The research results will reduce the energy consumption and improve the efficiency, which provide a theoretical basis for the design of automatic drilling sampling mechanism.

drilling sampling mechanism; hollow-external-screw drill stem; structural parameters; kinematic parameters; lunar-soil; sampling

2015-01-07; 退修日期: 2015-01-26; 录用日期: 2015-03-12； < class="emphasis_bold">网络出版时间：

时间：2015-03-30 15:00

www.cnki.net/kcms/detail/11.1929.V.20150330.1500.002.html

国家重大科技专项(TY3Q2011xxx01)

.Tel.： 010-68747342 E-mail: liuzhiquanymj@sina.com

王丽丽， 刘志全， 吴伟仁， 等． 月球钻取采样机构的钻杆结构与运动参数分析[J]． 航空学报, 2016, 37(2): 738-748. WANG L L, LIU Z Q, WU W R, et al. Analysis of drill stem structural and kinematic parameters of lunar drilling sampling mechanism[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 738-748.

http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn

10.7527/S1000-6893.2015.0075

V19

： A

： 1000-6893(2016)02-0738-11

*