基于改进Keystone变换的高速目标相参积累方法

赵 杰，郭德明，陈 果，倪国新

(南京电子技术研究所, 南京 210039)

·信号处理·

基于改进Keystone变换的高速目标相参积累方法

赵 杰，郭德明，陈 果，倪国新

(南京电子技术研究所, 南京 210039)

Keystone变换常常用于校正运动目标在脉冲多普勒雷达相参积累时间内的距离走动，提高回波信号的信噪比。但是常规Keystone变换应用于高速目标会存在两方面问题，首先常规Keystone变换引入插值增加了运算负担，其次若存在多普勒模糊，常规Keystone变换实现方法会出现“半盲速点”效应。文中提出了基于尺度变换的Keystone变换方法，新方法可以明显减少运算量，减小了带宽对多普勒模糊的影响，抑制了“半盲速点”效应，提高了相参积累效果。

距离走动； Keystone变换；尺度变换；“半盲速点”效应

0 引 言

随着雷达目标的雷达散射截面积(RCS)不断减小，超高速飞行器的出现，这些都对雷达的检测提出了新的挑战，成为了雷达急需解决的技术问题之一。文献[1-2]提出了通过增加信号积累时间提高雷达的检测能力，但是高速目标的宽带回波信号包络在积累时间内存在距离单元走动现象，增加了目标检测的复杂度。文献[3]提出了一种基于Hough变换的长时间积累算法，但是算法复杂且是非相参积累，效率较低。相参积累可以改善积累效率，但是必须解决积累时间内的距离走动问题。

针对高速目标在相参积累时间内出现的距离走动现象和高速目标存在的多普勒模糊问题，文献[4]提出的Keystone变换有效地校正了脉冲多普勒(PD)雷达的距离走动。该Keystone变换方法引入了sinc插值，运算量大，不利于工程实现。文献[5]和文献[6]提出了基于Chirp_z算法的Keystone变换，运用快速傅里叶变换和复乘运算，优化了运算，但文献[6]指出该方法在回波信号的信噪比较低时，相参积累效果明显下降。针对相参积累受限于目标运动，文献[7]提出一种基于Keystone变换的运动补偿方案，可以在没有目标运动速度信息条件下校正距离走动，从而使积累时间不再受目标运动的限制，文献[8]提出了“半盲速点”效应抑制和消除的方法，还需进一步优化引入插值运算带来的问题。针对Keystone变换在工程实践中遇到的计算量问题和“半盲速点”效应，本文将文献[9]提出的尺度变换应用于Keystone变换，该方法通过在慢时间域的复乘和快速傅里叶变换运算，消除了插值运算，解决了常规Keystone变换中运算量的问题，并结合“半盲速点”效应抑制算法，减小了带宽对多普勒模糊倍数区间的影响，能够快速的实现对距离走动的校正和对多普勒模糊的补偿，有效提高相参积累处理后信号的信噪比。

1 Keystone原理分析

本节将阐述Keystone变换意义，针对多普勒模糊问题改进Keystone变换，结合常用Keystone变换方法，分析基于尺度变换的Keystone变换的意义。

1.1 Keystone变换算法

假设雷达发射信号为线性调频信号，则第n个子脉冲发射信号表达式为

exp(j2πf0(t-nTr))

(1)

式中：t为时间；T0为线性调频信号的脉冲宽度；b为调频斜率；Tr为脉冲重复周期；f0为发射信号载频。令tn=nTr，称为慢时间，t′=t-tn，称为快时间，速度为v的点目标的初始距离为R0，回波信号经下变频处理后为

s(t′,tn)=Aa(t′-tn)exp(-j2πf0tn)

(2)

其中

为第n个脉冲的延迟时间。

对式(2)在快时间域做傅里叶变换,得到线性调频信号的频谱

s(f,tn)=Aa(f)exp(-j2π(f0+f)τn)=

Aa(f)exp(-j4π(f0+f)R0/C)·

exp(j4π(f0+f)vtn/C)=

Ap(f)exp(j4π(f0+f)vtn/C)

(3)

其中

p(f)=a(f)exp(-j4π(f0+f)R0/C)

(4)

式中：f为距离频率；指数项exp(j4πfvtn/C)表示距离频率和多普勒频率之间存在耦合，造成各个脉冲周期内的脉压结果不同，引起各个点目标回波信号的线性距离走动。通过对慢时间轴作变尺度变换，可以消除这一耦合，即Keystone变换。则

(5)

式中：tk为Keystone变换之后的虚拟慢时间。将式(5)代入式(4)，可得

s(f,tk)=Ap(f)exp(j4πf0vtk/C)

(6)

由式(6)可以看出，经过Keystone变换，回波信号的距离频率与目标速度的耦合相位得到了补偿。

高速目标常常会引入多普勒模糊问题，通常回波信号在多普勒模糊倍数已知的情况下，对式(6)乘以多普勒模糊补偿因子即可

(7)

但Keystone变换在长时间相参积累过程中存在“半盲速点”效应，除去插值影响Keystone性能外，信号频率对多普勒模糊影响如式(8)

(8)

式中：L为多普勒模糊倍数，若目标速度恰处于“半盲速点”附近，多普勒模糊倍数会出现突变现象，严重影响目标回波信号的积累效果。

为了减小带宽对多普勒模糊的影响，抑制“半盲速点”效应，Keystone变换前应先进行多普勒模糊补偿，即

p(f)exp(-j4π(f0+f)v0tn/C)

(9)

1.2Keystone变换实现的改进

本节将介绍sinc插值算法和Chirp_z算法，分析基于尺度变换的Keystone变换的原理。

常规的Keystone变换利用sinc插值算法实现信号在慢时间轴作变尺度变换，实现距离频率和多普勒频率的解耦合，其中m,n分别为处理前后慢时间的采样序列值，即

(10)

在多普勒模糊的情况下，对高速目标回波信号进行多普勒模糊补偿

(11)

Chirp_z算法应用于采样间隔不均匀时快速求取各采样值。文献[3]提出的Chirp_z算法实现了信号在虚拟慢时间tm对应的频域上进行变尺度离散傅里叶变换(DFT)变换，用循环卷积计算线性卷积，进而可以在频域使用快速傅里叶变换(FFT)实现快速计算，降低了插值方式下的Keystone变换的运算量。

文献[10]提出在聚束式SAR成像处理中，在距离域和方位域的重采样中应用尺度变换算法，有效地解决了散射点在距离单元和多普勒单元的运动补偿，该算法能够有效地实现时间维的尺度变换。本文将尺度变换引入PD雷达检测中，实现Keystone变换，为了抑制“半盲速点”效应，需先对回波信号进行多普勒模糊补偿，改进基于Keystone变换的多普勒模糊处理。

图1所示，基于尺度变换算法的Keystone变换可在时域完成变尺度变换，有效地处理“半盲速点”效应，其中n表示回波信号的慢时间采样序列，f为相应于快时间t的距离频率的采样序列。

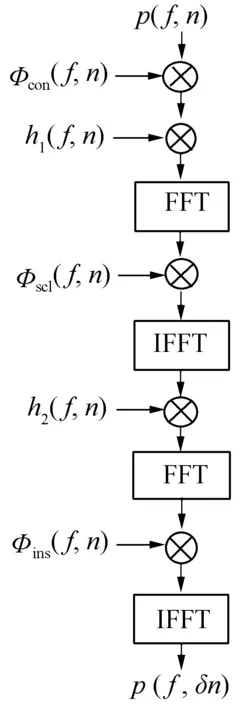
图1 基于尺度变换的Keystone变换流程图

回波信号需要先进行多普勒模糊补偿，减小多普勒模糊倍数突变区间，减少带宽对多普勒模糊的不利影响，较好地抑制“半盲速点”效应，提高距离走动校正后的相参积累效果。即

Scomp(f,n)=S(f,n)·Φcon(f,n)

(12)

式中：Φcon(f,n)为多普勒模糊补偿因子，即

(13)

此外，流程图中的两次复乘运算的算子，分别称为尺度因子和反尺度因子，其中fn为慢时间tn对应的多普勒频率，即

(14)

(15)

如流程图所示，在完成时间域的尺度变换过程中，系统还需要进行两次相位滤波，此过程可以通过快速傅里叶变换实现，滤波器的系统函数h1(f,fn)和h2(f,fn)定义如下

h1(f,n)=wa(n)exp(jnkαn2)

(16)

h2(f,n)=exp(-jπδKαn2)

(17)

式中：wa(t)是一个可选的权值因子，通常使用泰勒窗或汉明窗。系统函数h1(f,n)和h2(f,n)需满足大时间带宽积，其中式(16)满足大时间带宽积，且尺度变换因子应近似一。

参数δ取值由尺度变换因子决定，即

(18)

参数Kα取值受限于式(16)和式(17)的时带宽积，此外，尺度变换的中间结果频谱会对处理效果产生不利影响，故使其位于相位滤波的系统函数的带宽范围内。

本文用复数乘法次数表征计算量，设距离频率f的采样点数为N，相参积累时间内的脉冲个数为M，则一次sinc插值的计算量为NM2,一次相参积累的计算量为NM·(lbM)/2,一次模糊校正的计算量为NM，则上述三种Keystone变换实现算法的所需计算量如表1所示。

表1 Keystone变换实现算法比较

尺度变换算法在计算量方面相较于sinc插值算法优化明显，但较于Chirp_z算法优化不明显，但是回波信号的信噪比低于-16 dB时，Chirp_z算法相参积累出现明显下降，尺度变换算法较Chirp_z算法提高了在低信噪比情况下的处理效果，其可以在对距离走动作有效校正的前提下优化计算，有利于工程应用。

2 仿真分析

2.1 常规Keystone变换实现距离校正

仿真所需的雷达参数如下，载频f0=1 GHz，信号带宽B=30 MHz，脉冲宽度T0=100 μs，脉冲重复周期T=1 ms，一个CPI内发射的脉冲数np=128，目标相对雷达初始距离R0=35 km，信号的初始信噪比设为-16 dB，目标的径向运动速度v=310 m/s。

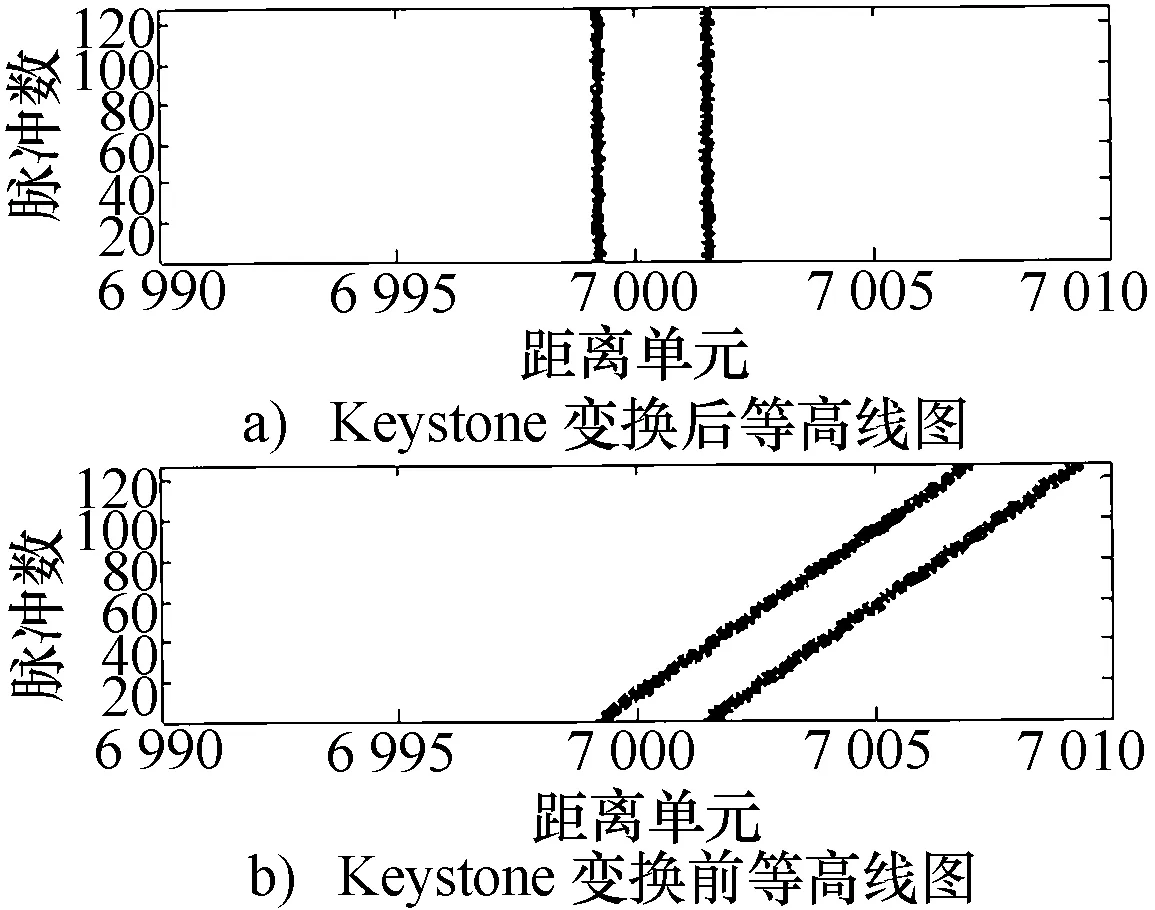
图2 Keystone变换校正前后回波信号的等高线对比图

目标在128个脉冲周期，即积累时间12.8 ms内的距离走动量δr=39.68 m，距离分辨率ΔR=5 m，由图2显示回波信号在第1个脉冲周期和第 128个脉冲周期之间跨距离单元数约为8个，与理论分析一致，图3显示经Keystone变换校正后，信号相参积累后的幅值得到很大提高，相参积累后信号的信噪比达18.7 dB,较回波信号直接进行相参积累的信噪比提高大约6.5 dB。

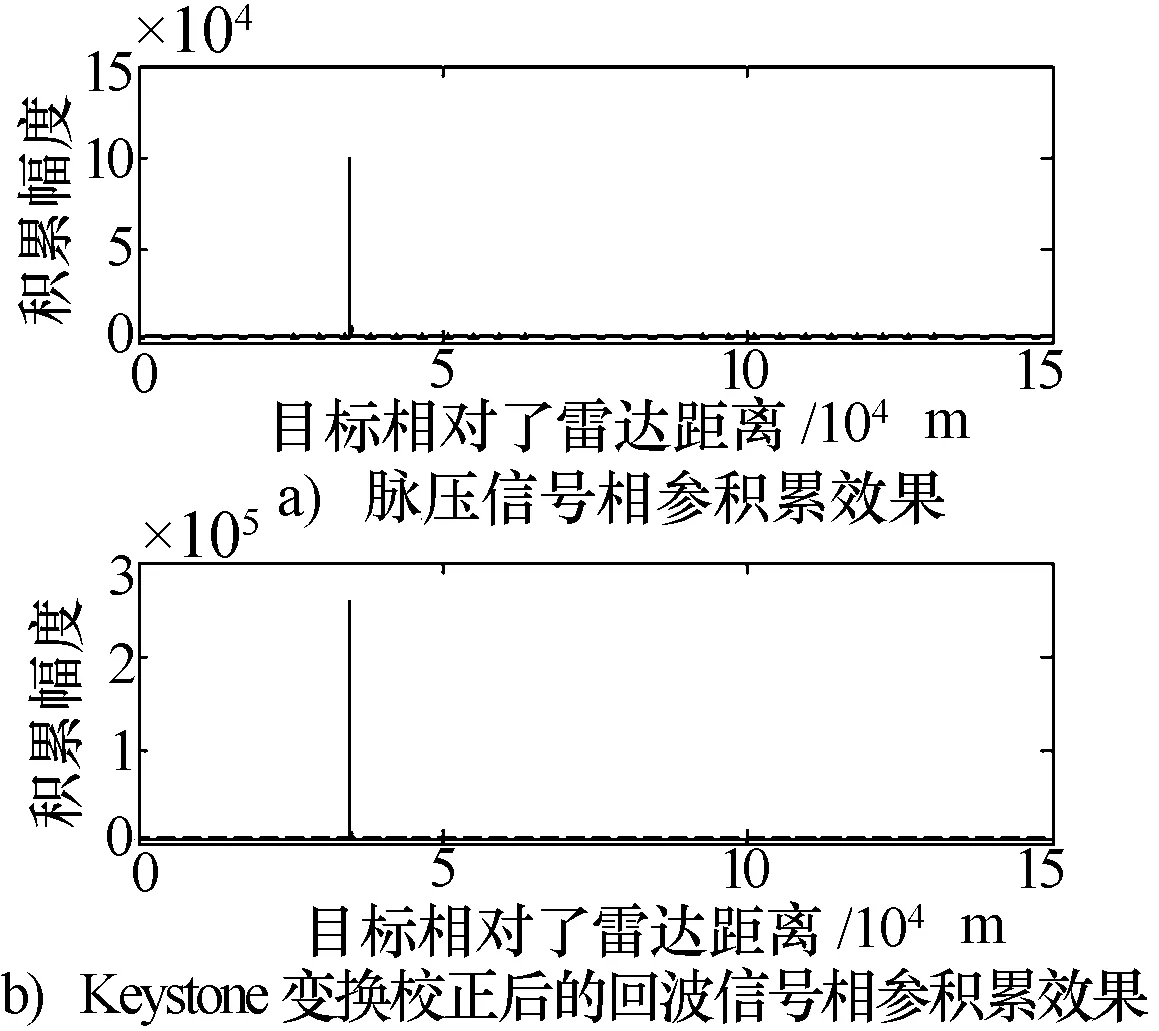
图3 Keystone变换校正前后回波信号相参积累效果对比图

2.2 “半盲速点”效应分析

仿真所需的雷达参数如下，载频f0=1 GHz，信号带宽B=10 MHz，脉冲宽度T0=100 μs，脉冲重复周期T=1 ms，一个CPI内发射的脉冲数np=128，目标相对雷达初始距离R0=35 km，信号的初始信噪比设为-16 dB，目标的径向运动速度v=370 m/s。

图4比较了“半盲速点”效应对高速目标回波信号相参积累性能的影响，从图4中可知“半盲速点”效应严重影响了Keystone变换的效果，通过对“半盲速点”效应做抑制处理后，信号相参积累后的信噪比达到20.4 dB，较未做抑制处理的结果提高了2 dB。因此，在校正距离走动的过程中，Keystone变换处理多普勒模糊问题应采用上述抑制“半盲速点”效应的方法，即先对多普勒模糊做补偿，再进行慢时间域的变换，可以提高Keystone变换的鲁棒性。

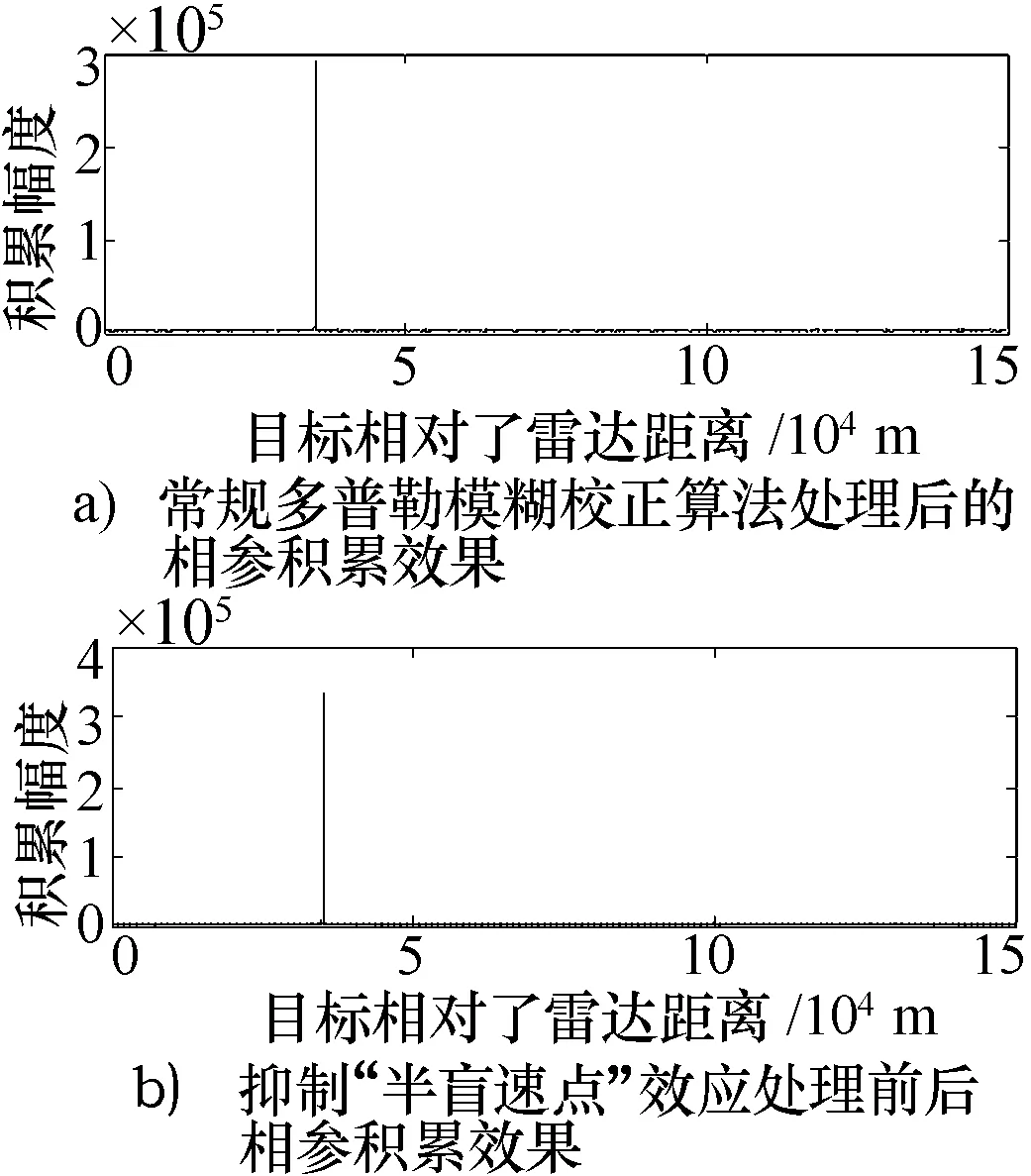
图4 “半盲速点”效应处理前后相参积累效果

2.3 Keystone变换实现方式比较

仿真所需的雷达参数如下，载频f0=1 GHz，信号带宽B=10 MHz，脉冲宽度T0=100 μs，脉冲重复周期T=1 ms，一个CPI内发射的脉冲数np=128，目标相对雷达初始距离R0=35 km，信号的初始信噪比设为-16 dB，目标的径向运动速度v=310 m/s。

图5比较了采用sinc插值和尺度变换两种算法实现Keystone变换后信号相参积累的效果。图5的上图是采用文献[3]提出的插值算法，未处理 “半盲速点”效应，下图采用了尺度变换算法，其处理后信号相参积累的信噪比大约为19.6 dB，运行时间为29.92 s，较插值提高了1 dB，节约了110 s左右。

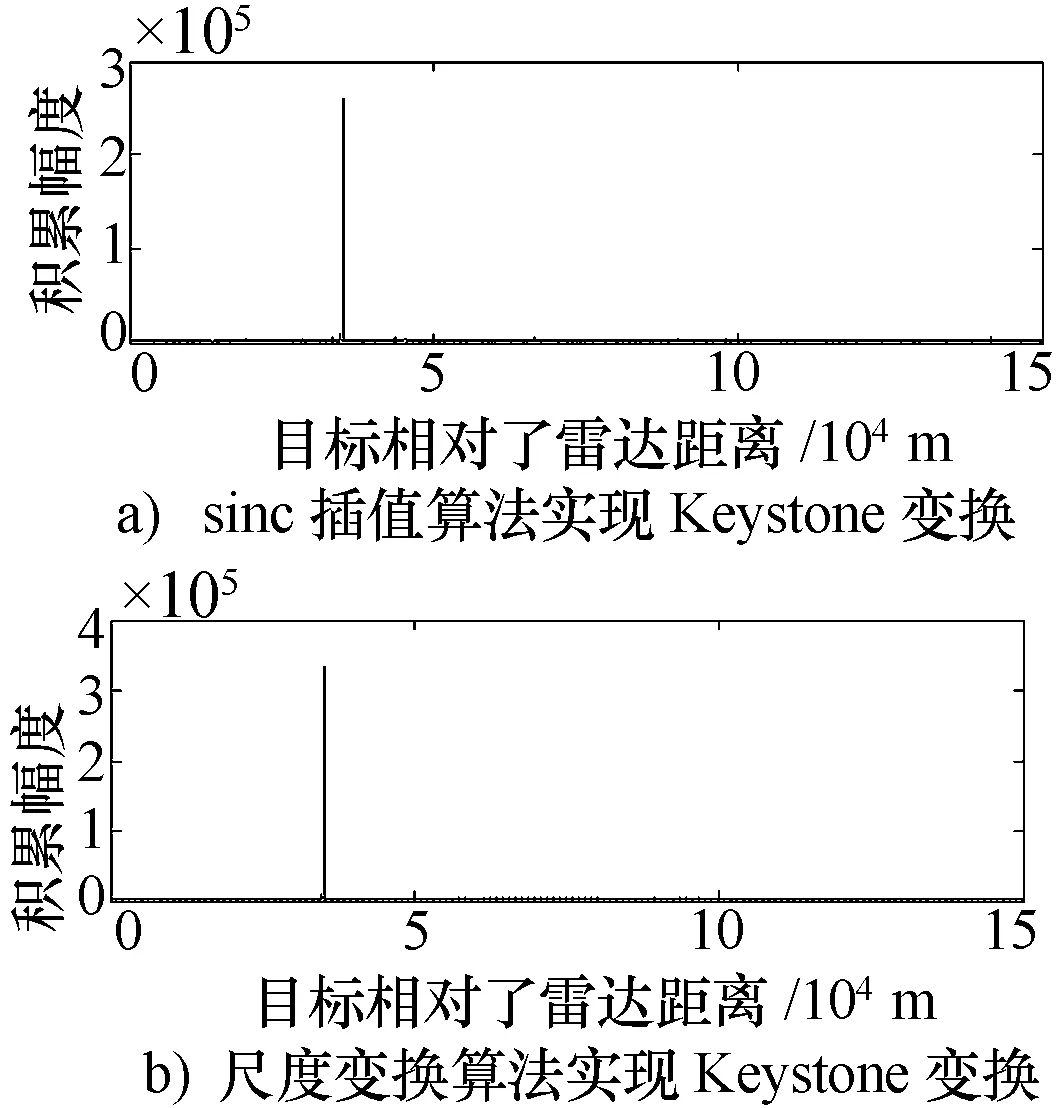
图5 Sinc插值和尺度变换实现Keystone变换的效果

图6比较了采用Chirp_z算法和尺度变换算法实现Keystone变换后信号相参积累的效果。图6的上图是采用文献[4]提出的Chirp_z算法，未处理 “半盲速点”效应，下图采用了尺度变换算法，其处理后信号相参积累的信噪比大约为19.63 dB，信噪比较Chirp_z算法提高了3 dB。

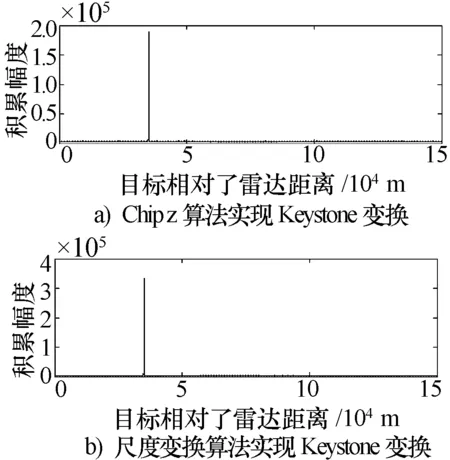
图6 Chirp_z和尺度变换实现Keystone变换的效果

3 结束语

雷达目标检测的效果取决于回波信号信噪比，相参积累可以有效提高低速目标回波信号的信噪比，但高速目标的回波信号在长时间积累过程中会出现距离走动现象，造成回波信号相参积累后信噪比下降，为了提高信号相参积累性能，本文应用Keystone变换校正高速目标回波信号处理的距离走动问题，但是传统Keystone变换常常存在计算量大、“半盲速点”效应引起多普勒模糊补偿性能下降等问题，本文针对上述问题，应用尺度变换算法实现Keystone变换，优化了计算，提高了对微弱回波信号的相参积累性能，并有效结合抑制“半盲速点”效应处理算法，有效补偿了在半盲速点附近的多普勒模糊，经仿真分析，改进后的Keystone变换算法可以有效地解决高速目标信号的距离走动问题，提高信号经相参积累处理后的信噪比，为目标检测奠定了基础。

[1] 李 海, 吴嗣亮, 莫 力, 等. 微弱信号长时间积累的检测方法[J]. 北京理工大学学报, 2001, 21(5): 614-617. LI Hai, WU Siliang, MO Li, et al. A method for long-term signal integral detection of weak targets[J]. Journal of Beijing Institute of Technology, 2001, 21(5): 614-617.

[2] 刘国靖, 王宏军, 秋 实. 短脉冲雷达模拟实验系统及目标探测初步实验研究[J]. 电子机械工程, 2001(3): 2-12. LIU Guojing, WANG Hongjun, QIU Shi. Short pulse radar simulation experimental system and basic experimental research on the target detection[J]. Electro-Mechanical Engineering, 2001(3): 2-12.

[3] MO Li. Radar detection of range migrated weak target through long-term integration[J]. Acta Electronica Sinica, 2003(4): 539-544.

[4] 张顺生, 曾 涛. 基于keystone变换的微弱目标检测[J]. 电子学报, 2005, 33(9): 1675-1678. ZHANG Shunsheng, ZENG Tao. Weak target detection based on keystone transform[J]. Acta Electronica Sinica, 2005, 33(9): 1675-1678.

[5] 王 娟, 赵永波. Keystone变换实现方法研究[J]. 火控雷达技术, 2011, 40(1): 45-51. WANG Juan, ZHAO Yongbo. Research on implementation of keystone transform[J]. Fire Control Radar Technology, 2011, 40(1): 45-51.

[6] 王 霞. 高速目标的跨距离门长时间积累研究[D]. 南京: 南京理工大学, 2014. WANG Xia. Research on the integration of high-velocity target across range-gate inlong time[D]. Nanjing: Nanjing University of Science and Technology, 2014.

[7] 张顺生, 曾 涛. 基于Keystone变换的微弱目标检测[J]. 电子学报, 2005, 33(9): 141-144. ZHANG Shunsheng, ZENG Tao. Weak target detection based on keystone translorm[J]. Acta Electronica Sinic, 2005, 33(9): 141-144.

[8] 洪永彬, 高梅国, 王俊岭, 等. Keystone变换半盲速点效应的抑制和消除[J]. 电子与信息学报, 2014, 36(1): 175-180. HONG Yongbin, GAO Meiguo, WANG Junling, et al. The supression and elimination of half blind velocity effect associated with keystone transform[J]. Journal of Electronics & Information Technology, 2014, 36(1): 175-180.

[9] ZHU D, LI Y, ZHU Z. A keystone transform without interpolation for SAR ground moving-target imaging[J]. IEEE Geoscience & Remote Sensing Letters, 2007, 4(1): 18-22.

[10] ZHU D, YE S, ZHU Z. Polar format agorithm using chirp scaling for spotlight SAR image formation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(4):1433-1448.

赵 杰 男，1990年生，硕士研究生。研究方向为雷达目标检测。

A Method of High-velocity Target Coherent Integration Based on Improved Keystone Transform

ZHAO Jie，GUO Deming，CHEN Guo, NI Guoxin

(Nanjing Research Institute of Electronics Technology, Nanjing 210039, China)

Keystone transform can correct range migration on the moving target in the PD radar coherent integration time, and improve the signal-to-noise ratio of the echo signal. But conventional Keystone transform applied to the high-velocity target will have two problems. Firstly, conventional Keystone transform increases computation burden with interpolation. Secondly, with Doppler ambiguity, 'half-blind-velocity effect' occurs when the conventional implementation method of Keystone transform is applied. The paper presents novel Keystone transform based on chirp scaling. It can obviously reduce computation cost and influence of bandwidth on Doppler ambiguity, suppress 'half-blind-velocity' and improve the performance of coherent integration.

range migration; keystone transform; scaling principle; half-blind-velocity effect

10.16592/ j.cnki.1004-7859.2016.04.008

赵杰 Email：zhaojie657@sina.com

2015-11-13

2016-01-27

TN911.7

A

1004-7859(2016)04-0034-04