关于足球弧线球运动轨迹的研究
2016-02-23郝成红黄耀清陆升阳段俊生
郝成红 黄耀清 王 欢 陆升阳 段俊生
(上海应用技术学院理学院,上海 201418)
关于足球弧线球运动轨迹的研究
郝成红 黄耀清 王 欢 陆升阳 段俊生
(上海应用技术学院理学院,上海 201418)
本文研究了足球弧线球运动的动力学方程,考虑马格努斯效应及相关参数的影响,得到了足球弧线球运动的轨迹曲线,为指导有关球类训练提供理论依据和参考.
弧线球;马格努斯效应;轨迹
现行大学物理教材在讨论斜抛运动时大多以质点为研究对象,很少涉及旋转物体的斜抛运动.实际上旋转抛体的运动是很常见的现象,尤其在球类运动项目中,球体在空中运动时,其自身往往伴随着旋转,例如:足球,乒乓球,篮球以及网球等.而球体自身的旋转必然影响到其运动的轨迹,也就是说,这种情况下,需要考虑马格努斯效应.当一个圆柱体绕自身轴线旋转并且有流体在垂直于该轴线方向流过时,它会受到一个垂直于流动方向的横向力,力的方向总是从来流方向与圆柱面上线速度相反的那一边指向相同的那一边,这种现象称为马格努斯(Magnus)效应,文献[1]写为马格纳斯效应.
实际上马格努斯效应并不局限于旋转的圆柱体,足球比赛中的所谓“香蕉球”、乒乓球比赛中的弧圈球及削球技术中都有马格努斯效应的明显作用[2].文献[3]~[7]讨论了“香蕉球”现象,但是大多仅局限于定性的讨论,而缺少定量的研究,并未给出严格的数学结果.本文将各类曲线运动的球体统称为弧线球,从动力学方程出发,研究弧线球的运动规律和轨迹.
1 动力学方程的解析解
如图1所示,我们以足球为例,设足球的质量为m,旋转角速度为ω,球体在旋转中运动时,由于马格努斯效应,除了受到重力作用之外,还要受到马格努斯力F[8,9]的作用,
F=μ(ω×)
(1)

图1 马格努斯力
式(1)中,μ是与流体(空气)的性质及物体几何形状、大小相关的常量.F的方向垂直于ω和所构成的平面,并满足矢量积的右手关系.建立图1所示的Oxyz三维直角坐标系,使球体旋转轴与z轴平行.Oxy面即为球场平面,z轴竖直向上.球体的初速度为0,0与Oxy面之间的夹角为α,0在Oxy面上的投影(大小为v0cosθ)与x轴的夹角为β.在理想状态下,即不考虑空气阻力时,则球体的动力学方程为
由式(2)得
(5)
将式(5)代入式(3),得
(6)
写成如下形式
(7)
此方程的解为
vx=vmcos(ω0t+φ)
(8)

得到
所以有
vx=v0cosαcos(ω0t+φ)
(13)
将式(8)代入式(5)得
vy=v0cosα·sin(ω0t+φ)
(14)
由式(4)得
vz=v0sinα-gt
(15)
式(13)、式(14)和式(15)对时间积分,可以得到坐标x,y和z与时间t的函数关系为
则球体的运动学方程为
r(t)=x(t)i+y(t)j+z(t)k
(19)
2 理论计算结果分析
对于式(16)、(17)和(18)来说,虽然原则上可以消去时间参量得到x(t)、y(t)和z(t)所满足的函数关系,但是对于结果分析并不方便.我们通过对上述3式的具体分析即可得到预期的结果.假设足球入射点在y轴上,由z(t)给出时间t,由x坐标的限定即可得到y值,或由既定的y值得到初速度或旋转角速度.
1) 由式(16)、(17)可以得到
(20)
2) 设y轴上G点是足球射门的入球点,令z(t)=0,根据式(18)可得t1=0(初始时刻对应x=0,y1=0),及
(21)
这个时间就是足球落地的时间,也就是入射球门左(或右)边底角的时间,在t2时刻仍取x=0,则y2为
(22)
3) 若考虑足球入射到球门的左(或右)上远角时,则需要取z=h(球门高度),代入式(18),得到方程
(23)
此方程的解为
(24)
由此可见这一组解要求
(25)
也就是对初速度v0的最小值有一个限定.
4) 当式(25)取等号时,则
(26)
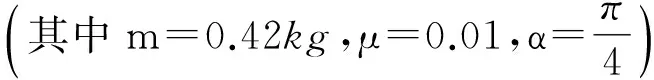
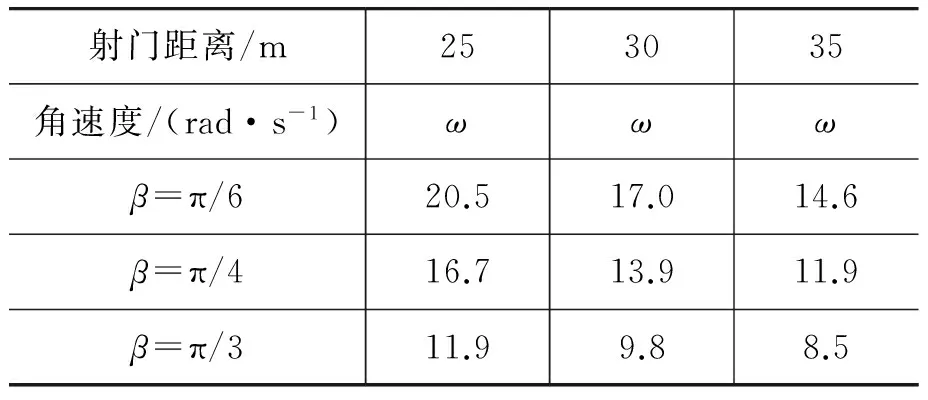
表1 射门距离和旋转角速度
6) 利用MATLAB软件可以做出三维立体轨迹如图2,图3和图4所示.

图2 α和β 均取固定参数
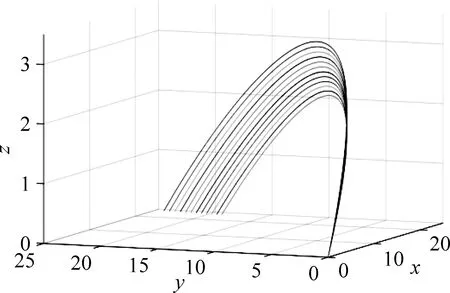
图3 α取不同值
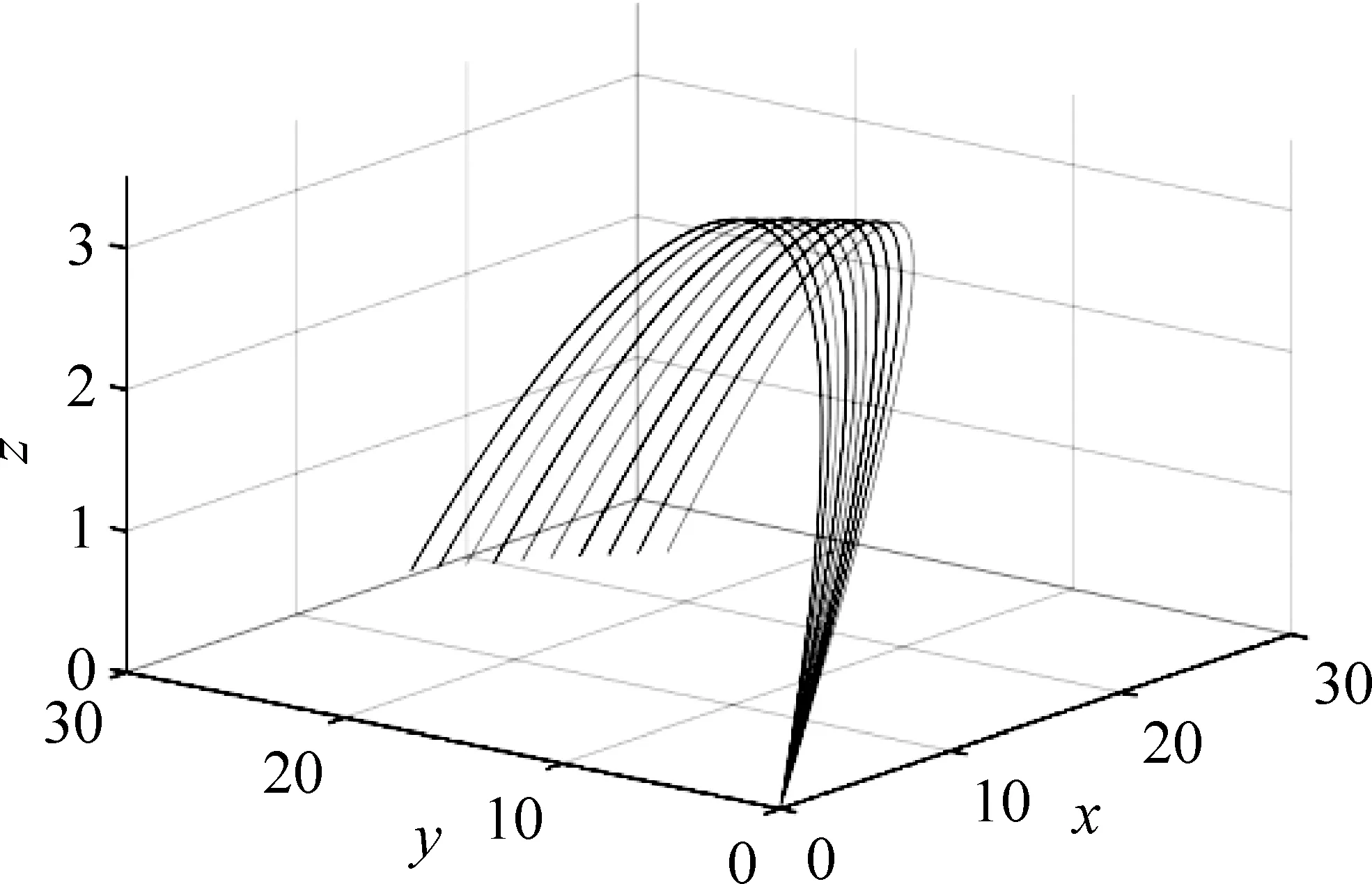
图4 β取不同值
其中图2的参数为:m=0.42kg,μ=0.02,ω=20π/s,v0=25m·s-1,α=π/10,β=π/32.
图3是保持β不变,α取不同值得到的一组曲线.
图4是保持α不变,β取不同值得到的一组曲线.
7) 当ω=0时,我们将式(16)和式(17)取ω→0的极限,则有
其中,vx0=v0cosα·cosβ;vy0=v0cosα·sinβ;vz0=v0sinα.
我们就得到了质点的斜抛运动的运动学方程.
旋转物体的斜抛运动与质点的斜抛运动的区别在于前者的运动轨迹是三维曲线,而后者则实际是二维的平面运动,如图5所示.
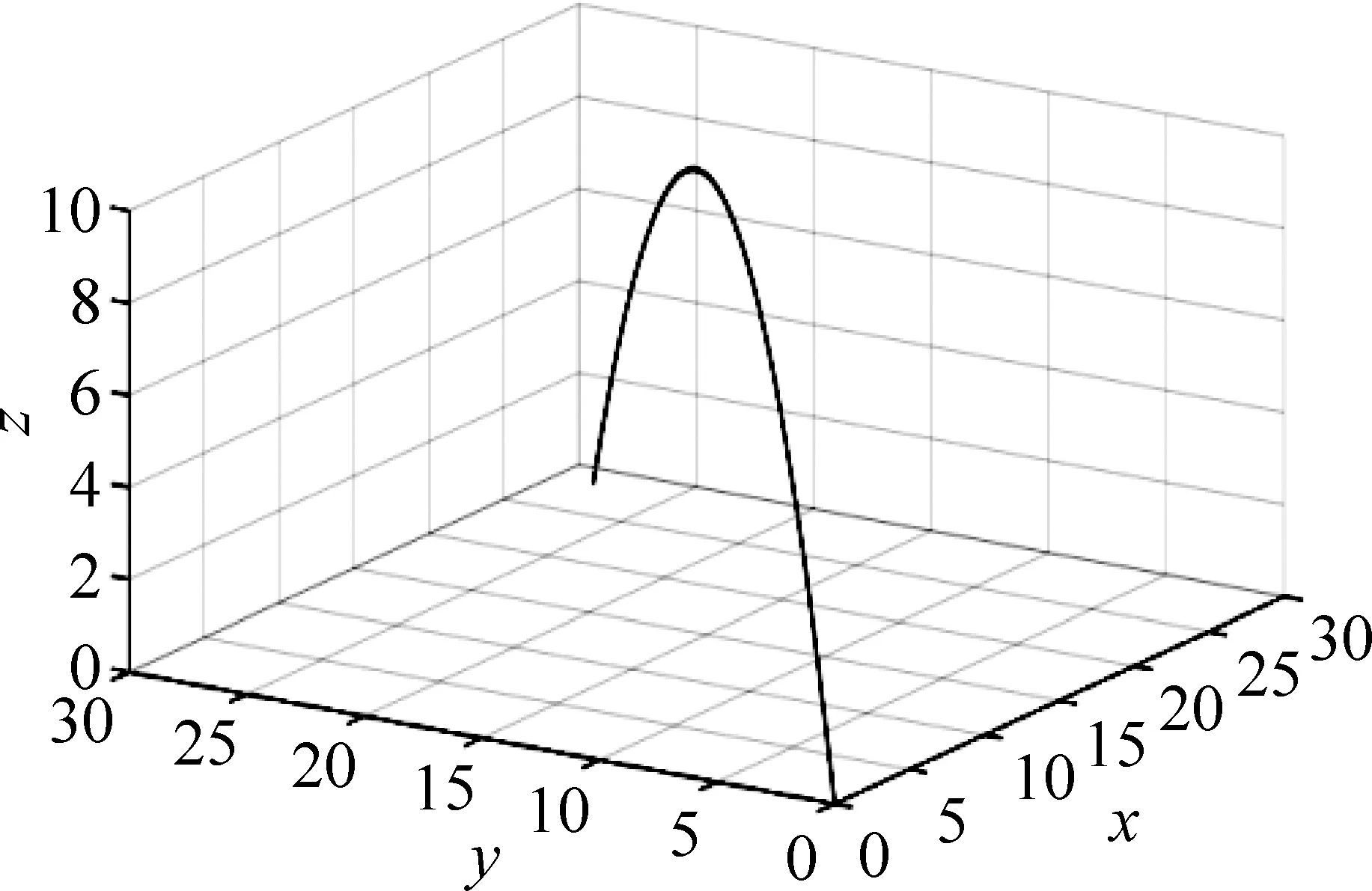
图5 α=π/4,β=π/4
3 结语
本文在三维直角坐标系中研究了弧线球运动的轨迹;得到了数学上的严格解析解,即给出了三维坐标与时间变量的函数关系.虽然是以足球为例得到的结果,但对于相关球类来说其结果具有普遍意义.可以为相关球类的技术训练提供理论根据和计算方法;也为进一步深入研究提供基础性的结果.
[1] 赵凯华,罗蔚茵.新概念物理教程·力学[M].2版.北京:高等教育出版社,2015:231.
[2] 漆安慎,杜婵英.普通物理学教程·力学[M].北京:高等教育出版社,1997:374.
[3] 葛隆祺.弧线球运动规律的探讨[J].大学物理,1991(7):26-28.
[4] 王伟,刘欣.浅谈“香蕉球”的力学原理[J].体育文献科技通报,2008,6(3):43.
[5] 赵进宝.球类运动中的流体力学问题[J].力学与实践,1988,10(6):33.
[6] 刘大为.球体飞行轨迹异常的探讨[J].大学物理,1987(1):43.
[7] 葛隆祺,叶卫军.足球旋转球的运动规律[J].物理通报,1999(2):7-8.
[8] http://farside.ph.utexas.edu/teaching/329/lectures/node43.html[9] http://www.nennstiel-ruprecht.de/bullfly/magnusf.htm#header
■
STUDY ON MOTION LOCUS OF BANANA KICK
Hao Chenghong Huang Yaoqing Wang Huan Lu Shengyang Duan Junsheng
(School of Science, Shanghai Institute of Technology, Shanghai 201418)
Considering the Magnus effect and relating parameter, kinetics equation of banana kick in football game is solved and motion locus of banana kick is given in this paper. It can provide theoretical foundation and reference for some kinds of ball trainings.
banana kick; Magnus effect; locus
2015-11-13;
2016-02-04
郝成红,男,上海应用技术学院理学院副教授,从事大学物理教学及研究工作.
黄耀清,女,上海应用技术学院理学院教授.huangyaoqingsit@126.com
郝成红,黄耀清,王欢,等. 关于足球弧线球运动轨迹的研究[J]. 物理与工程,2016,26(5):79-81,84.
