杨氏双缝干涉条纹的空间分布及理论模拟
2016-02-23何坤娜
何坤娜 黄 坚
(1中国农业大学理学院,北京 100083;2北京航空航天大学软件学院,北京 1000191;3江苏现代城市交通技术协同创新中心,江苏 南京 211189)
杨氏双缝干涉条纹的空间分布及理论模拟
何坤娜1黄 坚2,3
(1中国农业大学理学院,北京 100083;2北京航空航天大学软件学院,北京 1000191;3江苏现代城市交通技术协同创新中心,江苏 南京 211189)
杨氏双缝干涉实验中,观察屏上条纹的分布是授课的重点内容.现有的大学物理教材,大都通过分析经过近似的光程差表达式,得出观察屏上干涉条纹是等间距的直条纹的结论,但该结论并不能真实反映条纹的空间分布情况.本文结合立体几何知识,在未经任何近似情况下,推导出了干涉明、暗纹的空间分布所满足的双叶旋转双曲面方程,并在该方程基础上对传播空间和观察屏上明纹分布进行了理论模拟,模拟结果形象直观,有助于学生对干涉条纹特点的整体理解和掌握.
双缝干涉;光程差;双叶旋转双曲面
杨氏双缝干涉实验中,观察屏上的条纹分布是授课过程中的一个重点内容.现有的大学物理教材,大都在分析后给出了屏幕上干涉条纹是等间距的明、暗相间的直条纹的结论[1-4],但该结论是从分析光程差的近似表达式得到的,因此并不能真实反映空间条纹的分布情况.事实上,杨氏双缝实验中观察屏上干涉条纹的分布应是一系列双叶旋转双曲面和观察屏的交线,是一系列双曲线,而且观察屏上的条纹分布仅仅只是干涉条纹在空间分布的一部分,但仅少数教材[5]提到这一点,且并未有详细说明.本文结合立体几何知识,给出了双缝发出的光在空间传播过程中发生相干干涉时明、暗条纹分布所满足的数学表达式——双叶旋转双曲面方程,并对光传播空间明纹的立体分布及观察屏上明纹的分布进行了理论模拟,模拟结果将数学公式的物理意义形象直观地展示了出来,有利于学生理解和全面掌握干涉条纹的分布.
1 明、暗干涉条纹在空间的立体分布所满足的双叶旋转双曲面方程
由于杨氏双缝干涉图样与双孔干涉图样相比,屏幕上条纹分布完全相同,只不过双缝干涉条纹更亮些,因此,分析杨氏双缝实验的干涉图样时,为了描述方便,我们以双孔干涉为例来进行分析.图1为双孔干涉实验的光路示意图,设双孔S1、S2的间距为d,O为双孔S1、S2的中点,P为光传播方向上空间内任意一点,设点P与双孔S1、S2的距离分别为r1和r2,则光程差Δr=r2-r1,且Δr为空间坐标的函数,记为Δr(x,y,z).根据光的干涉的相关理论,当光程差满足公式
Δr(x,y,z)=kλ,k=0,±1,±2,…,±n
(1)
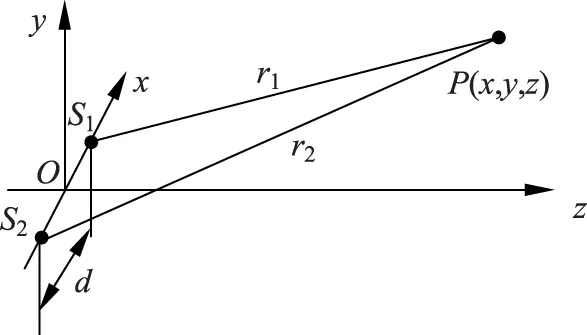
图1 杨氏双孔干涉实验光路示意图
时,光传播方向上满足公式(1)的空间点应为亮点,而k值相同的亮点连起来构成第k级明纹.当光程差满足公式
(2)
时,光传播方向上满足公式(2)的空间点应为暗点,而k值相同的暗点连起来构成第k级暗纹.因此,只要确定Δr(x,y,z)的表达式,就能根据公式(1)和公式(2)确定不同级次的明、暗条纹在空间的分布,而根据几何学知识,Δr=r2-r1=C(常量)的轨迹是以S1和S2的连线为旋转轴的双叶旋转双曲面.
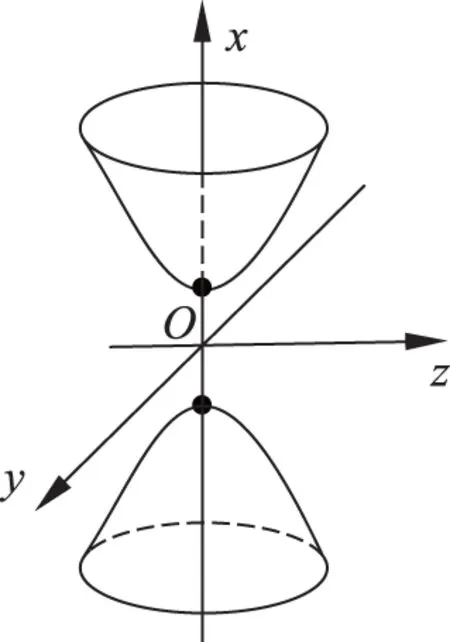
图2 双叶旋转双曲面
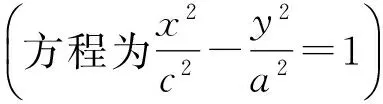
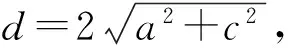
(3)
该方程的物理意义为:间距为d的两点光源发出的光在空间传播的过程中,相位差r2-r1=kλ的点在空间连成的曲面(为一个亮面).
同理,可得暗纹分布所满足的双叶旋转双曲面方程为
(4)
由于双孔干涉实验中只考虑沿z轴正向传播的光即可,因此,在z轴正向距离坐标原点z处放一观察屏,观察屏与双叶旋转双曲面的交线即为观察屏上能观察到的条纹分布.
根据公式(3)和(4),通过改变参数z、d以及级次k,可分别模拟不同级次明、暗纹在空间的立体分布及观察屏上的明、暗干涉条纹分布.由于公式(3)和(4)形式类似,因此,明、暗纹分布特点应类似.为了说明问题,我们仅就明纹分布进行模拟.模拟过程中,设入射单色光波长为λ=500nm.
Matlab(Matrix Laboratory)是美国Mathwork公司推出的一款功能强大的教学软件包,Matlab不但具有强大的数值计算功能,而且具有超强的可视化功能,可以将理论模拟结果形象直观地展示出来,本文中的模拟结果均基于Matlab软件来完成.
2 不同情况下,明条纹分布的理论模拟结果
(1)d=0.1mm时, 0级、±1级和±2级明纹所对应的双叶旋转双曲面在空间的立体分布及z=1.5m位置处观察屏与双叶旋转双曲面的交线如图3所示.
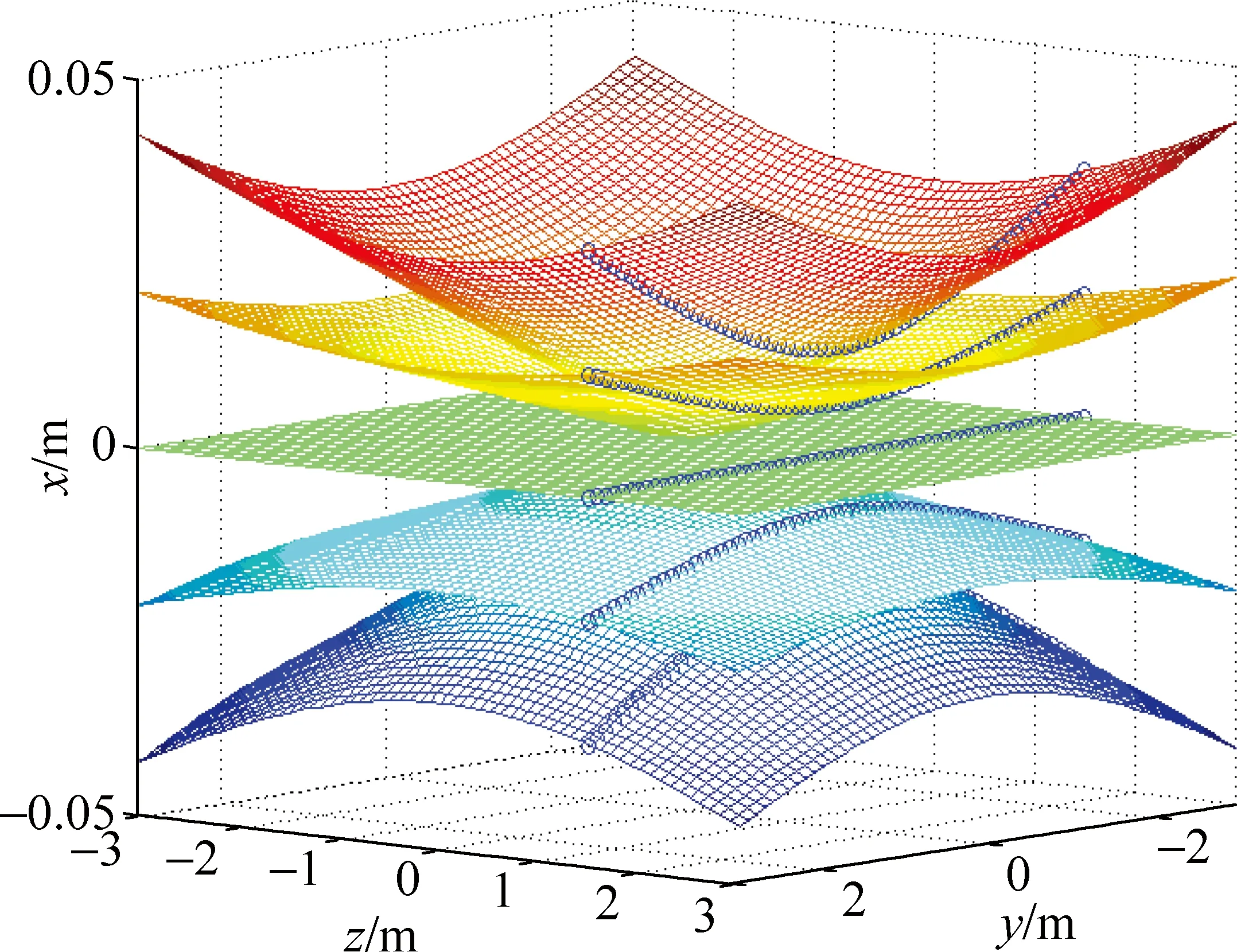
图3 d=0.1mm时, 0级、±1级和±2级明纹在空间的立体分布及z=1.5m位置处观察屏与双叶旋转双曲面的交线
图3中能看到的0级、±1和±2级明纹.图3中的坐标轴x、y、z分别与图1的坐标轴x、y、z相对应.由图3不难看出,观察屏上除中央明纹外,中央明纹两侧对称的干涉明纹应是一对对双曲线,并非平行直条;改变观察屏位置,屏上明条纹的分布情况不同.
(2) 图4为d=0.1mm时,z=0.5m、1.5m、2.5m处观察屏上较大范围内的干涉条纹分布.
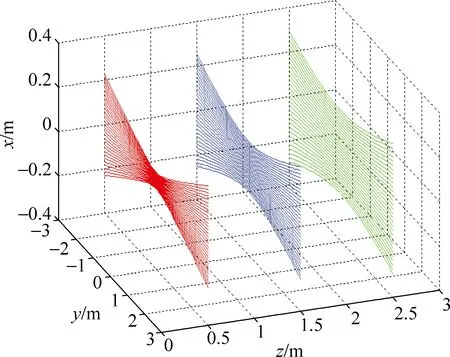
图4 d=0.1m,z=0.5m、1.5m、2.5m处观察屏上干涉条纹分布(只模拟了中央明纹及其两侧±15级明纹)
很明显,相比图3,图4可更清晰地展示观察屏在不同位置时屏上条纹分布.由图4可知,随着z增加,明纹在x方向的分布范围逐渐加宽;当z分别为0.5m、1.5m和2.5m时,屏幕上明条纹均是平行于xy平面的一系列双曲线,并不是等间距的直条纹,但是,观察屏离xy平面越远,双曲线的弯曲程度越小.
(3) 当d=0.1mm时,z=0.5m、1.5m、2.5m远处观察屏上较小观察范围内干涉条纹分布,如图5所示.
由图5可知,当z为0.5m时,级次大的干涉条纹还能看出一定的弯曲,但中央明纹两侧附近的条纹已接近直线分布;当z为1.5m和2.5m时,干涉条纹呈平行等间距直线分布,这与大多数物理教材中经过近似推导后得到的结论一致,即如明暗干涉条纹同时考虑,观察到的应该是等间距的明、暗相间的直条纹.图5(2)和图5(3)中呈直线分布的k级明纹在观察屏上的位置应满足关系式(5),相邻两明纹间距满足关系式(6).
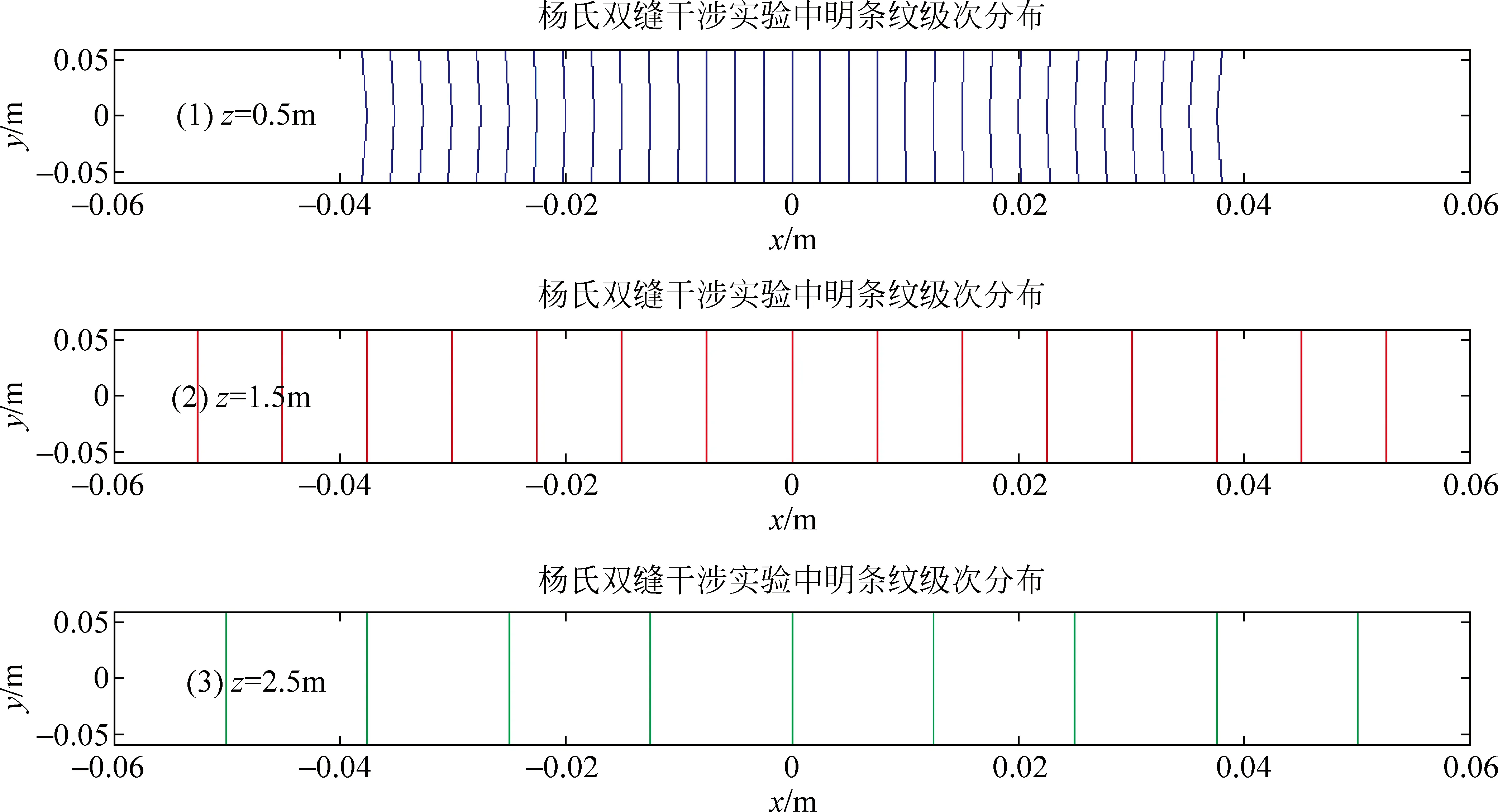
图5 当d=0.1mm时,z=0.5m、1.5m、2.5m远处观察屏上较小观察范围内干涉条纹分布(观察范围在±0.12m2)
另外,由图5可知,当z为0.5m时,条纹间距较小,条纹比较密集,±15级仍都能全部显示出来.随着z增大,条纹间距增大,干涉明纹条数减小.当z分别为1.5m和2m时,屏幕上明条纹数量分别为15条和9条(只能显示至±7级和±4级).
3 结语
本文结合立体几何知识,推导出了杨氏双缝干涉实验中明、暗干涉条纹在空间分布所满足的双叶旋转双曲面方程,并对明纹分布进行了理论模拟.模拟结果将数学公式的物理意义形象直观地展示了出来,有助于学生对条纹分布特点的理解和掌握.模拟结果表明:杨氏双缝实验中观察屏上干涉条纹的分布应是一系列双曲线,但当坐标原点和屏幕之间距离z远大于两孔间距d时,在屏幕上不大的观察范围内,观察到的是一系列平直条纹.
将本文理论模拟结果与一般物理教材中得到的条纹分布特点(条纹分布是等间距的明、暗相间的直条纹)相比,不难看出,一般物理教材中给出的条纹分布特点实际上仅是本文中一定条件下的(z≫d,同时在屏幕上不大的观察范围内)理论模拟结果.但是,本文的模拟结果只能直观展示条纹是等间距直线,并未明确给出直条纹在屏幕上的位置所满足的规律,而一般物理教材中,在分析近似光程差的基础上明确给出了明(暗)直条纹位置所满足的关系式.因此,本文理论模拟结果结合一般物理教材中杨氏双缝干涉部分的相关理论推导结果,可使学生对干涉条纹有比较全面的认识,即不仅能了解干涉条纹在空间的整体分布情况,而且可以明确一定条件下平直条纹的分布规律.
[1] 张三慧.大学基础物理学[M].北京:清华大学出版社, 2003:592-593.
[2] 马文蔚,周雨青,解希顺.物理学教程[M].2版.北京:高等教育出版社, 2006:185.
[3] 程守洙,江之永.普通物理学[M].5版.北京:高等教育出版社,1998:175-176.
[4] 吴百诗.大学物理[M].西安:西安交通大学出版社,2008:118-119.
[5] 金仲辉,柴丽娜.大学基础物理学[M].3版.北京:科学出版社,2010:260.
■
STUDY AND SIMULATION ON THE SPATIAL DISTRIBUTION OF INTERFERENCE PATTERN IN YOUNG’S DOUBLE-SLIT INTERFERENCE EXPERIMENT
He Kunna1Huang Jian2,3
(1College of Science, China Agricultural University, Beijing 100083;2School of Software, Beihang University, Beijing 100191;3Jiangsu Province Collaborative Innovation Center of Modern Urban Traffic Technologies, Nanjing Jiangsu 211189)
In Young’s double-slit interference experiment, the fringe pattern on the observation screen is the focus of teaching. Existing college physics teaching material mostly drew a conclusion that the interference fringes are equally spaced by analyzing the approximate expression of the optical path difference. However, this conclusion can’t really reflect the spatial distribution of the fringe pattern. The paper first derived a hyperboloid equation of two sheets of revolution, which described the pattern of the high and low amplitudes that are generated by the two waves in Young’s double-slit interference experiment; then further simulated the high amplitudes distribution on the propagation space and the screen. The whole experiment and simulation is vivid and convenient for the student to better understand the characteristic of the interference pattern.
double-slit interference; light path difference; two sheets of revolution
2015-11-24;
2016-03-10
何坤娜,女,讲师,主要从事大学物理的教学工作以及新型激光器件与技术等方面的研究.hekunna@cau.edu.cn
黄坚,男,讲师,主要从事大学计算机教学工作,以及计算机辅助的数据分析与模拟计算研究工作.hj@buaa.edu.cn
何坤娜,黄坚. 杨氏双缝干涉条纹的空间分布及理论模拟[J]. 物理与工程,2016,26(5):12-15.
