不同迎角和速度下充气式返回舱气动性能预测
2016-02-23赵晓舜余莉杨雪
赵晓舜 余莉 杨雪
(南京航空航天大学航空宇航学院,南京 210016)
不同迎角和速度下充气式返回舱气动性能预测
赵晓舜 余莉 杨雪
(南京航空航天大学航空宇航学院,南京 210016)
减速是返回式航天飞行器必须面对的关键性问题。充气式返回舱通过降低返回系统的质量增加了有效载荷,具有质量轻、易折叠包装、展开阻力面积大,再入时弹道系数低和产生的气动热量小等优点。文章以美国 NASA的充气式返回舱(IRV-3)为研究对象,采用有限体积法进行了不同速度和迎角下的流场数值计算。研究对比了充气式返回舱在粘性模型和无粘模型下的流场数值结果,发现无粘模型在超声速情况下能满足一定的精度要求,提高了计算稳定性和计算效率。考察了不同迎角、速度下充气式返回舱的气动性能,结果表明阻力系数随着马赫数增加升高之后再逐渐降低,在Ma=5时气动阻力最大;合适的迎角可以降低俯仰力矩系数,增加返回舱的稳定性;迎角在小角度变化时,俯仰力矩系数和升力系数变化较大,而阻力系数变化较小。文章的研究结果对充气式返回舱的设计及分析有一定参考意义。
充气式返回舱气动性能 计算流体动力学 粘性模型 航天返回
0 引言
随着深空探测技术的发展,传统的第一代刚性再入返回舱由于质量大[1]、有效载荷小等诸多限制已经无法满足探测的需要[2-4],第二代柔性充气式再入返回舱作为一种新技术应运而生。充气式返回舱是一种新型充气式再入飞行器,不仅具有质量轻[5]、可折叠包装、收拢体积小[6-7]等优点,而且其展开气动外形在再入过程中可提供满足工作要求的阻力,表面的柔性防热材料还能承受较高的温度环境[8-9]。充气式返回舱技术受到国际航天界的高度关注[10]。
美国NASA研究的充气式返回舱以前抛型充气气囊(Inflatable Re-entry Vehicle, IRV)为代表,它是一种堆叠圆环型充气式返回舱[11]。美国曾先后进行了3次飞行试验,分别验证了在气动力载荷作用下充气壳结构保形能力、弹道性能和材料特性。在数值仿真方面,NASA对充气式和刚性返回舱的气体动力学进行了数值仿真,对比了它们在不同迎角下阻力系数[12],对IRV-4测试的充气式返回舱结构采用有限元方法进行动态特性分析,与实验对比分析了织物材料的抗载荷能力[13]。随着中国空间活动的日益频繁和深空探测项目的启动,我们也将面临各种不同体积质量载荷的回收问题和探测器在其他行星上的进入问题,充气式减速技术的预先研究工作也渐渐开始进行。北航已经制造出了一个最大直径 3m,头锥角90°的充气式防热罩原理样机,用以进行相关技术的探索和验证[14];文献[15]采用ANSYS对堆叠圆环型的结构进行静力学分析;文献[16]等对温度场、热应力及变形进行了数值计算,文献[17]对两次充气和单次充气式返回舱的再入弹道进行了比较分析。但是国内对于不同速度迎角情况下充气式返回舱的气动性能的研究文章还比较少。
本文以NASA的IRV-3为研究对象,分别采用粘性模型和无粘模型,基于ICEM和FASTRAN软件开展了不同迎角和速度下的数值仿真,分析了粘性对于数值计算结果的影响,考察了迎角和速度对IRV-3气动性能的影响。本文的研究结果对充气式返回舱的设计及分析有一定参考意义。
1 控制方程
流体力学的控制方程分为连续方程、动量方程和能量方程。控制方程分别遵循着的三大物理规律是质量守恒、牛顿第二定律和能量守恒。本文中无粘模型忽略了粘性力对于流体运动的影响,而粘性模型是包含粘性力的完整控制方程。
1.1 无粘模型
无粘模型流动忽略了流动中的运输和粘性耗散现象,控制方程如下:

式中 ρ为流体密度;Lj、vj为x、y、z的任一方向坐标分量和相对速度分量。

式中 Li、vi为区别于j坐标的坐标分量和区别于j坐标的平均相对速度分量;p为压强。

式中 E为总能量;H为总焓;qj为某一方向的热通量。
1.2粘性模型
充气式返回舱工作时运动速度很大,为三维粘性可压缩流动。粘性模型的连续性方程、动量方程和能量方程分别为:
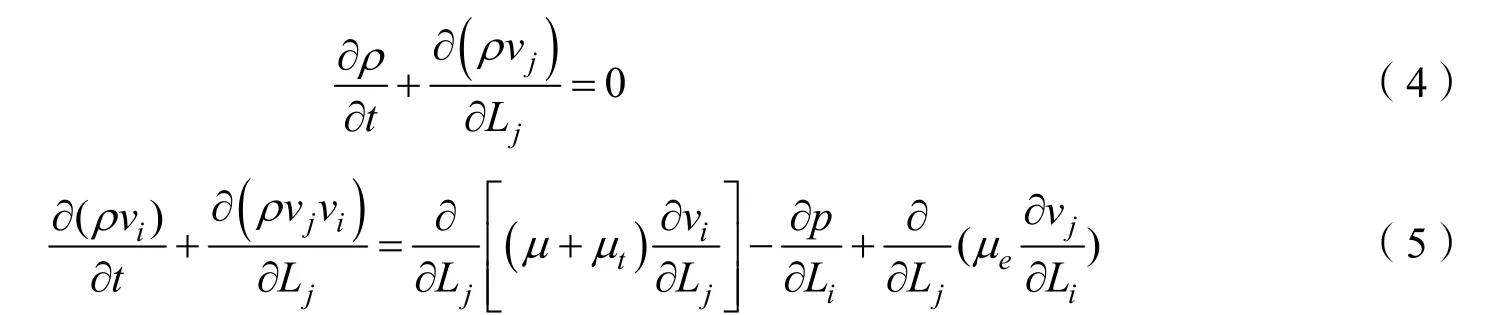
式中 μ为分子粘性系数;tμ为湍流涡粘性系数;eμ为有效粘性系数。
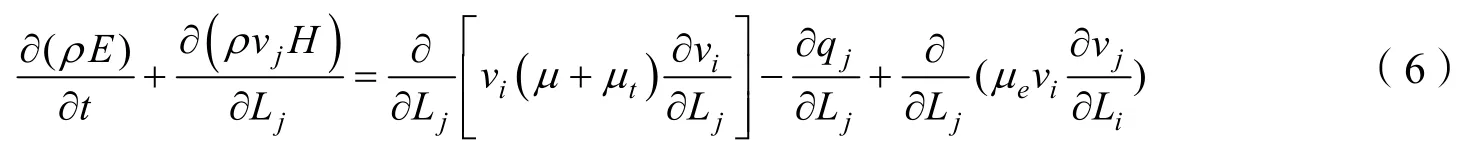
为了得到粘性模型湍流方程的解,本文引入的k-ε湍流模型来封闭。补充方程如下:
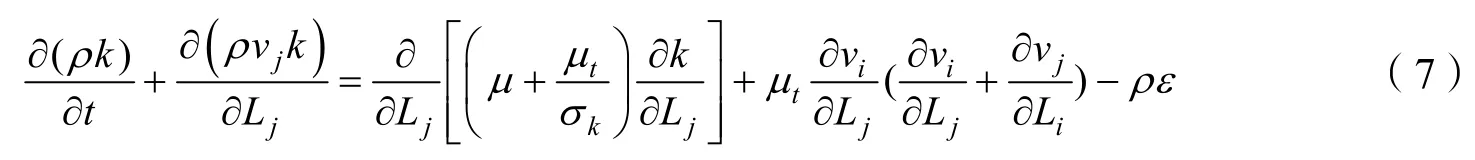
式中 k为湍流动能;ε为湍流耗散率;计算参数(取值来自于FASTRAN软件帮助文档)kσ=1.0。
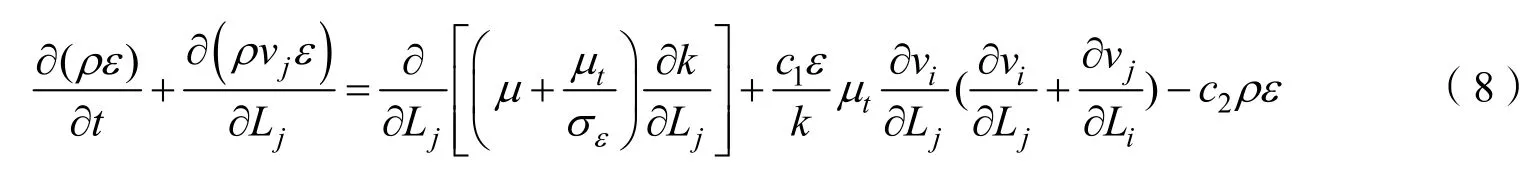
式中 计算参数(取值来自于FASTRAN软件帮助文档)c1=1.44;c2=1.92;kσ=1.3。
2 算例验证
本文数值计算采用有限体积法进行,其中无粘模型通量采用Roe格式[18],粘性模型通量采用中心差分格式离散,时间离散均采用隐式LU-SGS方法[19]。为验证本文数值计算的可靠性,由于公开文献无法检索到IRV-3的不同迎角速度下的实验数据,以文献[20]的圆柱形钝头体为对象(此钝头体半径为0.05m),以此来开展高超音速粘性模型的流场计算。计算工况为:来流Ma=8,流场初始静压强是855Pa,温度是1 726K,壁面温度设定为恒温294K且无滑移[20]。
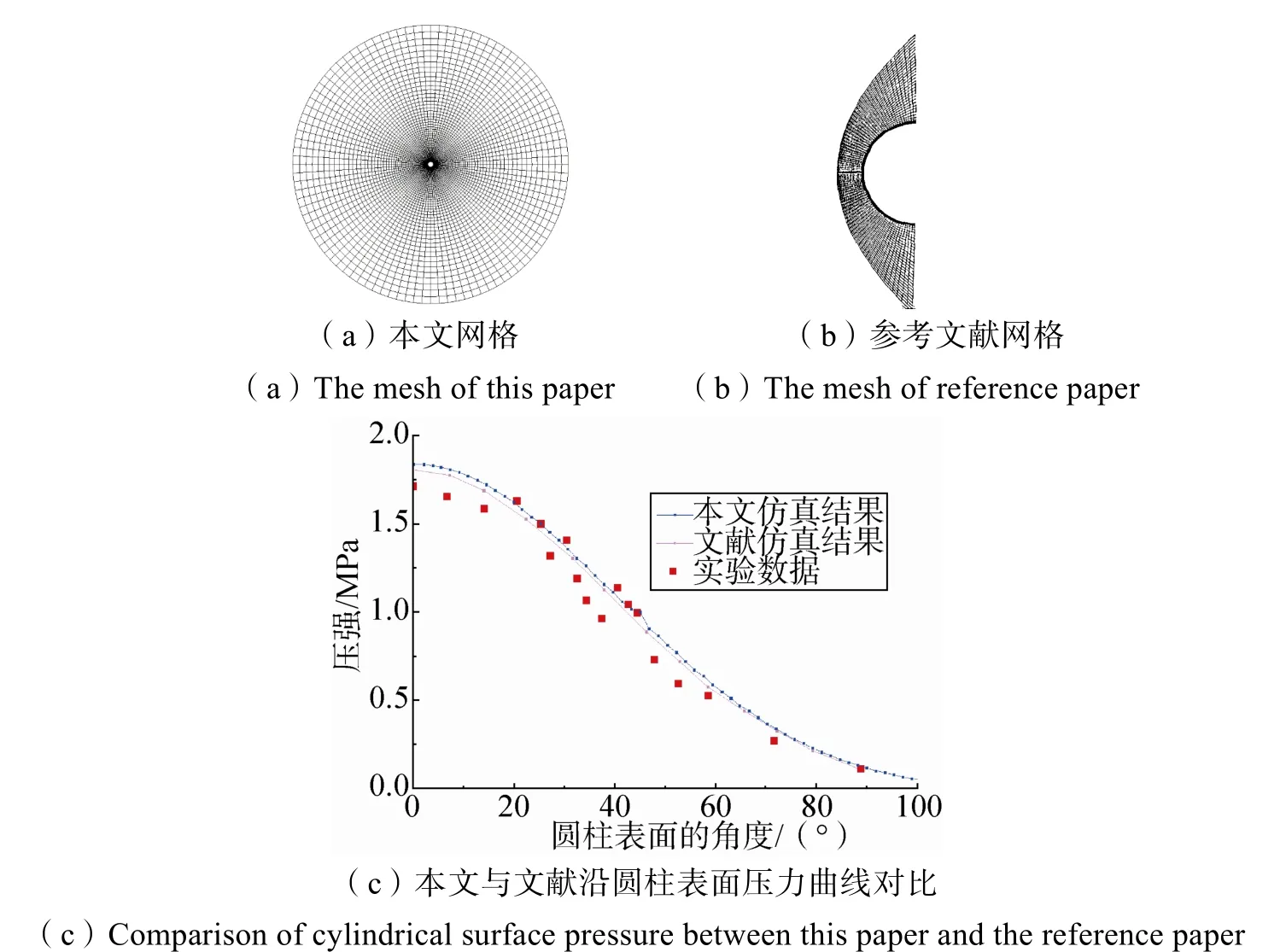
图1 本文与文献的流场网格和圆柱表面压力曲线对比Fig.1 Comparison of cylindrical surface pressure and flow field grid between this paper and the reference paper
文献[20]中给出了数值仿真沿圆柱表面0°~90°的压力变化曲线以及风洞实验数据。图1中(c)图为本文与文献[20]沿圆柱表面压力曲线对比,可以看出本文数值仿真结果和文献计算结果吻合很好,趋势一致,和风洞实验数据相比压力的误差在 6%以内。可见针对超声速流场计算本文采用的数值方法具有较高的一致性。
3 数值模型
IRV-3的实体模型和几何尺寸如图2。充气式返回舱的直径和高度分别为3.0m和1.6m,环形结构直径为0.3m,半锥角为60°,中心体直径为0.39m。由于充气圆环内部为保压的结构,变形小,本文将其内部充气圆环简化为连通结构,将充气式返回舱简化为刚体模型。采用ICEM软件建立了充气式返回舱的流场分块结构化网格,如图3所示。为了模拟火星再入环境,将来流气体的环境设置为地球50km处,来流气体环境的参数如表1所示,此时温度为270.65K,压强为75.77Pa。采用有限体积方法进行计算,壁面设置为无滑移绝热壁。
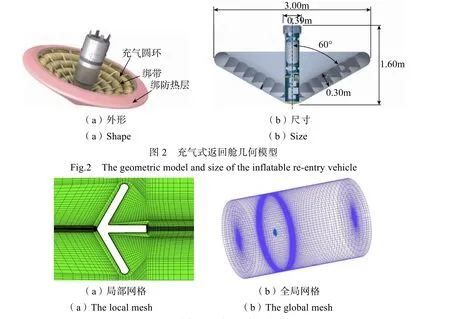
图3 充气返回舱的流场网格Fig.3 The flow field mesh of inflatable reentry vehicle

表1 计算仿真的环境模型Tab.1 The environmental model of CFD
网格数量对计算准确性及计算消耗均有很大的影响,本文在0°迎角,Ma=5工况下对IRV-3开展了网格相关性测试,网格数量从100万至350万共6种,计算结果如图4所示,纵坐标表示充气式返回舱阻力系数Cd、升力系数CL、俯仰力矩Cm随着网格数cell的变化情况。计算结果表明,当网格数大于200万时,气动系数变化趋势减小,网格数的增加对计算结果影响不大,反而会大大增加计算消耗。最终确定数值计算流场网格数为240万,其中壁面第一层网格尺寸为0.015mm。
4 无粘模型和粘性模型的对比
图5、图6为不同速度下无粘模型和粘性模型下流场对比和气动系数的变化:Ma≤4粘性模型中摩擦、热传导等耗散使得返回舱圆环处分离点前移,前部压强小于无粘模型,阻力系数变小;Ma≥4两种模型的流场特性相差无几,两种模型的阻力系数相差很小(图6);Ma=1时,粘性模型使得流过返回舱时边界层分离点提前,导致粘性模型上下压差较大,升力系数更高,而在Ma≥2以上,二者相差不大(图6)。对上述结果进行分析认为:随着速度的升高,雷诺数逐渐增大,惯性力相对于粘性力的比值增加,惯性阻力作用增强,粘性力影响减弱。可见随着速度的增加粘性模型对于气动系数的影响越来越小,在Ma≥4的超声速区域使用无粘模型计算可以保证工程计算精度,提高计算稳定性和计算效率。
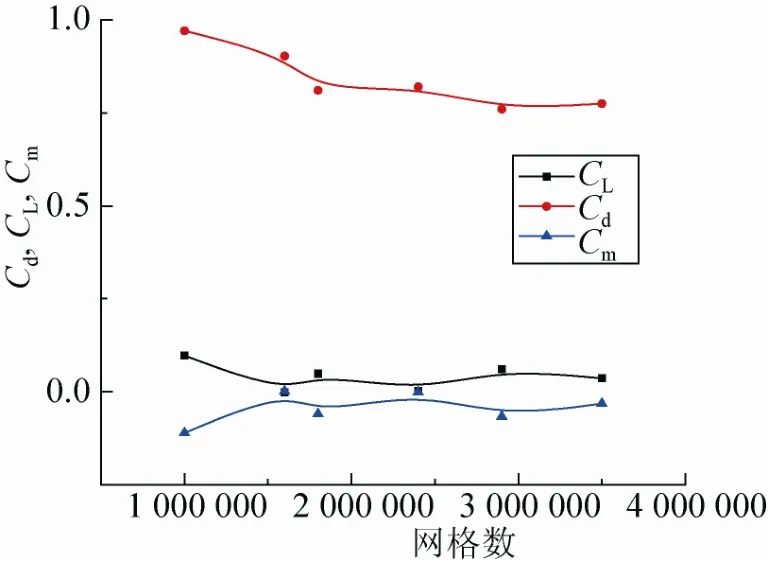
图4 充气式返回舱网格模型Fig.4 The mesh of the inflatable re-entry vehicle
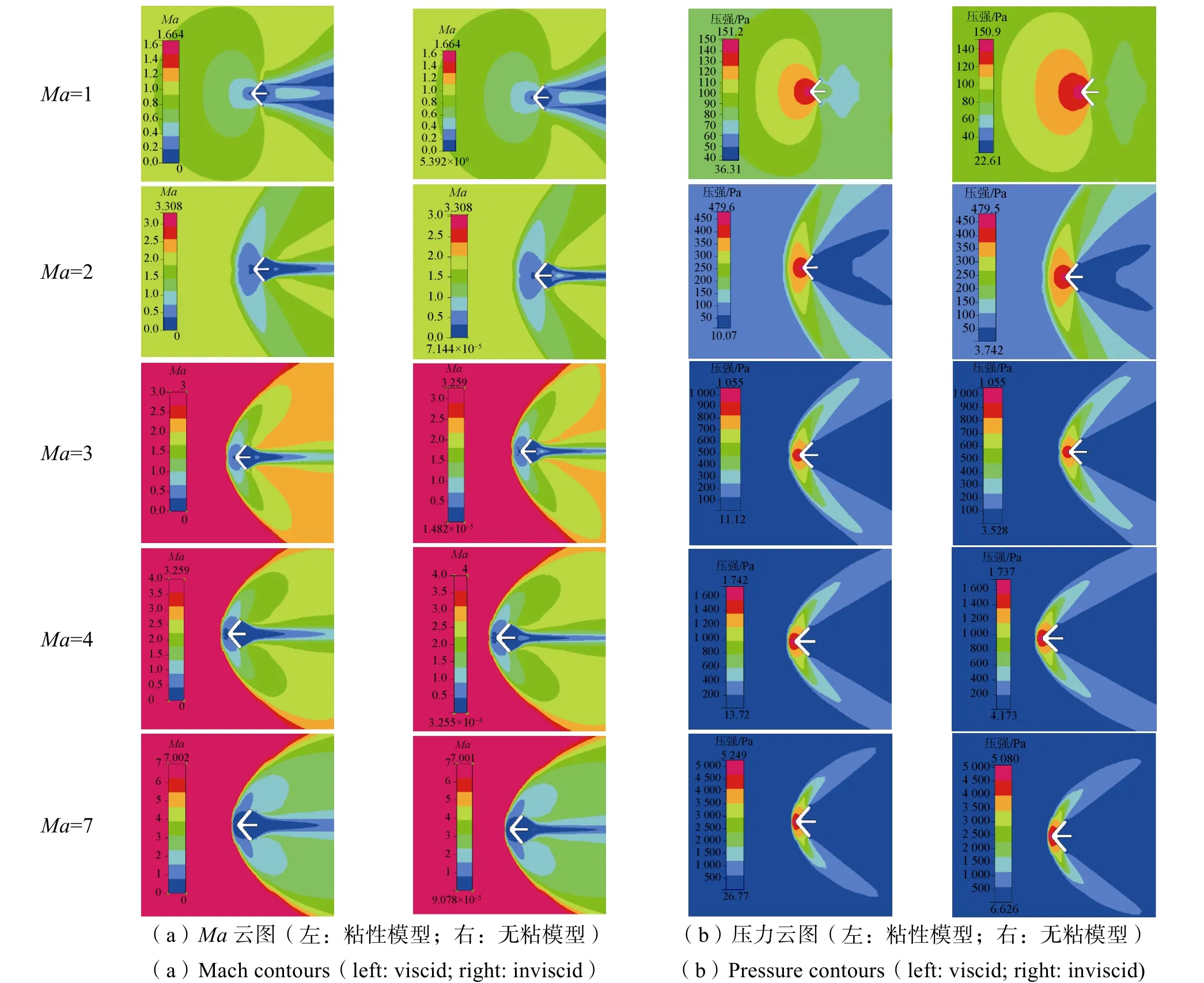
图5 不同速度下无粘模型和粘性模型下流场对比Fig.5 The flow field of viscid model and inviscid model at different speed
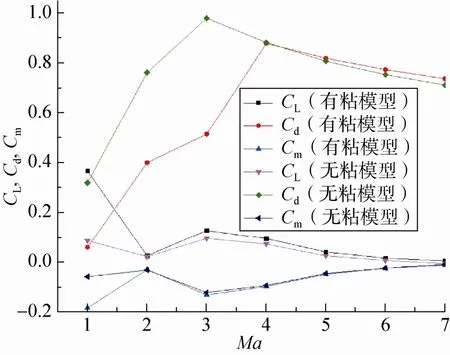
图6 不同速度下的气动系数的变化Fig.6 The aerodynamic coefficient at different speed
5 粘性模型下迎角速度影响分析
图7和图9分别为不同迎角和不同速度下返回舱的流场,图8和图10分别为气动系数随迎角及速度的变化曲线。
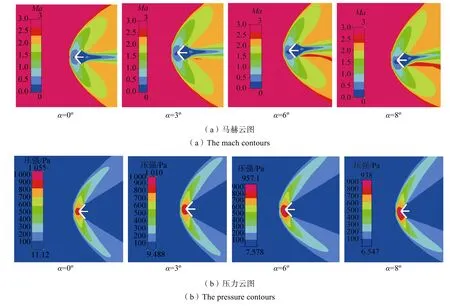
图7 不同迎角下返回舱的流场(Ma=3;迎角α=0°,3°,6°,8°)Fig.7 The mach and pressure contours of IRV at different attack angle
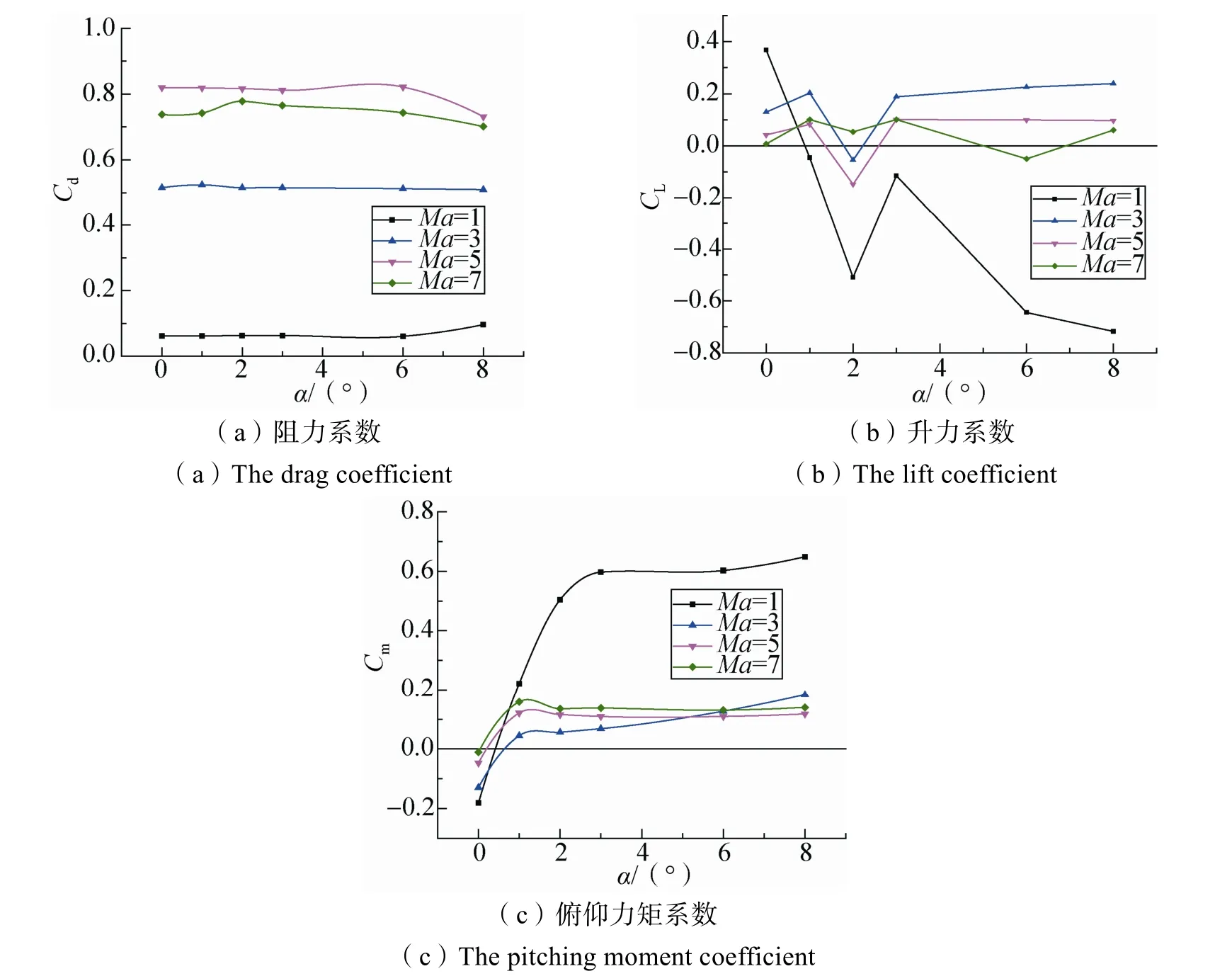
图8 迎角对气动系数的影响Fig.8 The influence of angle of attack on aerodynamic coefficients
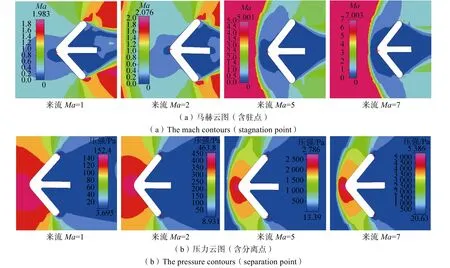
图9 不同Ma下返回舱的流场(迎角α=3°;Ma=1、2、5、7)Fig.9 The mach and pressure contours of IRV at different Mach
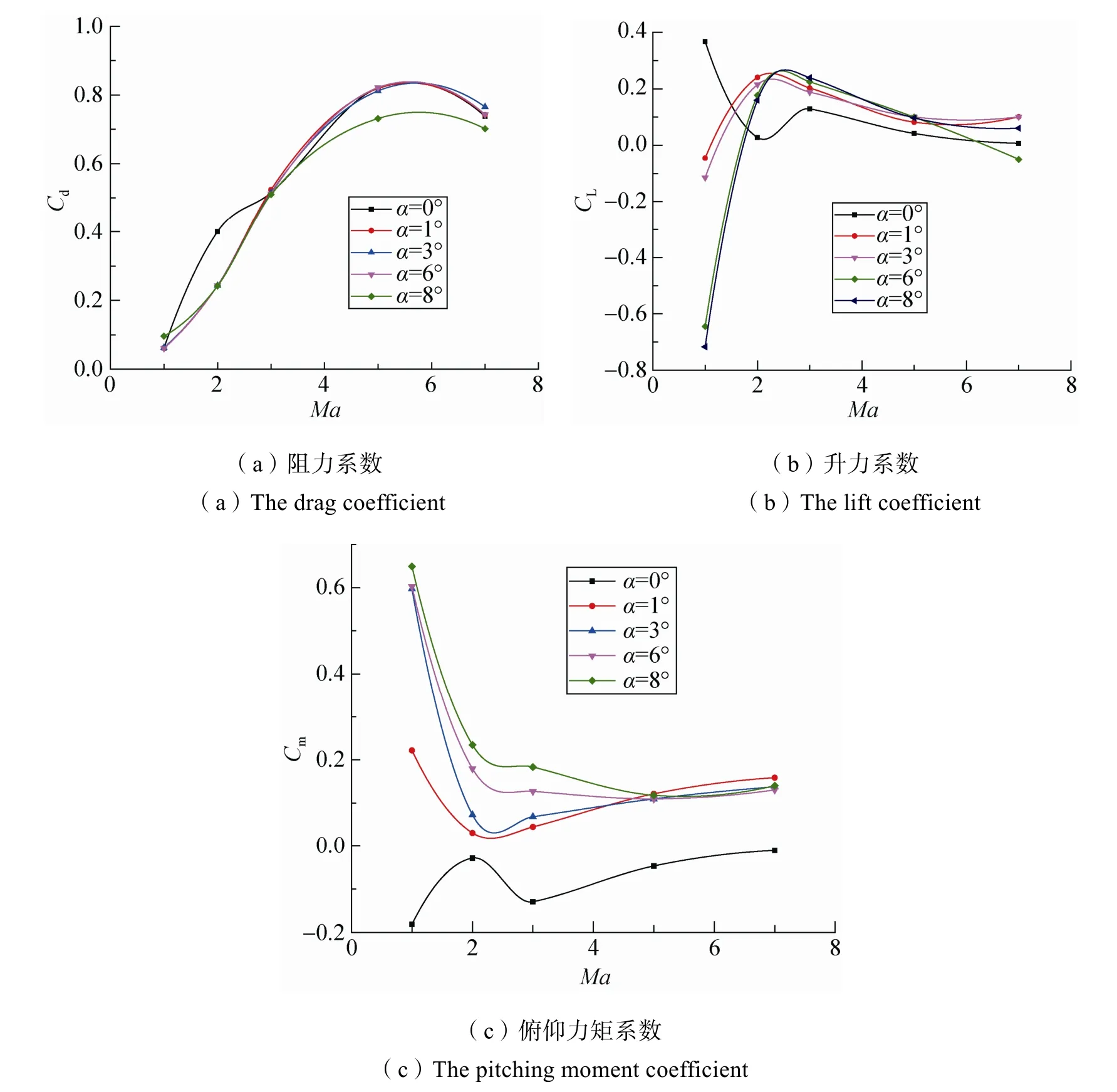
图10 速度对气动系数的影响(不同迎角下)Fig.10 The influence of speed on aerodynamic coefficients(at different attack angles)
由图7~10可以看出,随着迎角的增加,返回舱尾涡向上偏转,流场不再对称,返回舱尾部下方出现高马赫区并且不断增大;返回舱前方驻点向下翼面移动,压强由1 055Pa下降到938Pa;下翼面高压区不断扩大,返回舱稳定性降低。迎角的改变对返回舱的升力系数和力矩系数会产生比较大的影响。
随着速度的增加,尾涡区变得更为细长,弓形激波夹角减小,前翼面压强增加幅度大于后翼面使得前后压差的增大,此时阻力系数随速度的增加,而当速度大于Ma=5时,前翼面压强的增加幅度小于后翼面压强增加,前后压差减小使得阻力系数下降。速度的增加使分离点向后移动,驻点由下翼面向上移动,膨胀波影响区域越来越大,返回舱后部压力变得更加均匀,升力和俯仰力矩变小;在Ma≤2时,返回舱后部膨胀波较强对尾涡影响较大,Ma越小后部不对称压差增加,升力系数绝对值更大,俯仰力矩变化也较大。
6 结束语
充气式返回舱具有很好的环境适应性及优良的减速性能,在航天器回收减速领域具有很好的发展前景。本文采用数值模拟方法考察了超音速情况下无粘模型对计算准确性的影响,研究了迎角及速度变化对返回舱气动性能的影响。得出以下结论:
1)随着速度的增加粘性力对于阻力系数的影响越来越小;当Ma≥4时,无粘模型的计算结果与粘性模型计算结果相差很小;但无粘模型计算稳定性优于粘性模型,计算时间更短。
2)迎角增加,驻点向下翼面移动,流场不再对称,稳定性降低,返回舱的升力系数和力矩系数影响较大,而阻力系数受迎角影响较小。
3)速度增加,分离点向后移动,返回舱尾涡区变得更为细长,弓形激波夹角减小,返回舱的阻力系数会升高之后再逐渐降低,Ma≥5时气动阻力最大;当Ma≤2时,临近跨音速区,尾部流场变化剧烈,上下压力变化更为敏感,升力系数和俯仰力矩变化较大。
References)
[1]ALKANDRY H, BOYD I D, REED E M, et al. Interactions of Single-nozzle Sonic Propulsive Deceleration Jets on Mars Entry Aeroshells[J]. Spacecraft and Rockets, 2011, 48(4): 564-572.
[2]RICHARDSON E H, MUNK M M, JAMES B F. Review of NASA In-space Propulsion Technology Program Inflatable Decelerator Investments[C]//18th AIAA Aerodynamic Decelerator Systems Technology Conference, Munich, 2005.
[3]陈国良, 高树义. 中国航天器回收着陆技术50年成就与展望[J]. 航天返回与遥感, 2008, 29(3): 27-32. CHEN Guoliang, GAO Shuyi. The Development and Prospect of Spacecraft Recovery and Landing Technology in the Last Fifty Years in China[J]. Spacecraft Recovery &Remote Sensing, 2008, 29(3): 27-32. (in Chinese)
[4]KENDALL R T. Development and Use of Inflatable Payload Recovery Vehicles[R]. AIAA 92-0888-CP, 1991.
[5]LINDELL M C, HUGHES S J, DIXON M, et al. Structural Analysis and Testing of the Inflatable Re-entry Vehicle Experiment (IRV)[C]//47th AIAA/ASME/ASCM/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Rhode Island, Newport, 2006: 1-4.
[6]卫剑征, 马瑞强, 谭惠丰, 等. 单充气环薄膜型返回舱气动特性分析[J]. 航天返回与遥感, 2013, 34(7): 882-883. WEI Jianzheng, MA Ruiqiang, TAN Huifeng, et al. Analysis of Aerodynamic Characteristics of Inflatable Membrane Aeroshell[J]. Spacecraft Recovery and Remote Sensing, 2013, 34(7): 882-883. (in Chinese)
[7]FURUYA H, NAKAHARA M, MURATA S, et al. Concept of Inflatable Tensegrity for Large Space Structures[R]. Newport: 47th AIAA Structures, Structural Dynamics, and Materials Conferences, 2006.
[8]沈祖炜. 可膨胀再入防热锥的技术进展[J]. 航天返回与遥感, 2001, 22(2): 1-6. SHEN Zuwei. Inflatable Re-entry Shield of Payload Recovery Technology[J]. Spacecraft Recoery and Remote Sensing, 2001, 22(2): 1-6. (in Chinese)
[9]LINDELL M C, HUGHES S J, DIXON M, et al. Structural Analysis and Testing of the Inflatable Re-entry Vehicle Experiment (IRVE)[C]//Newport: 47th AIAA Structures, Structural Dynamics, and Materials Conferences, 2006.
[10]李爽, 江秀强. 火星进入返回舱技术综述与展望[J]. 航空学报, 2015, 36(2): 422-440. LI Shuang, JIANG Xiuqiang. Review and Prospect of Decelerator Technologies for Mars Entry[J]. Journal of Astronautics, 2015, 36(2): 422-440.(in Chinese)
[11]WILDE D, WALTHER S. Flight Test and ISS Application of the Inflatable Reentry and Descent Technology (IRDT) [J]. Acta Astronautica, 2002, 51(1-9): 83-88.
[12]MURMAN S M. Dynamic Simulations of Atmospheric-entry Capsules[J]. Journal of Spacecraft and Rockets, 2009, 46(4): 829-835.
[13]LITTON D K, BOSE D M. Inflatable Re-entry Vehicle Experiment (IRV)-4 Overview[C]//21st AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Ireland, Dublin, 2011: 23-26.
[14]九州虫. 膨胀的野心—美国 IRV-3任务带给我们的启示[EB/OL]. [2012-08-06]. http://blog.sina.com.cn/s/ blog_5387c42f0102dzbs.html.JIU Zhouchong. The Vaulting Ambition-the Enlightenment of IRV-3 Mission in the United States Gives Us[EB/OL]. [2012-08-06]. http://blog.sina.com.cn/s/blog_5387c42f0102dzbs.html. (in Chinese)
[15]贺卫亮, 才晶晶. 一次发射多次返回的充气式再入飞行器技术[J]. 载人航天, 2011(4): 37-42. HE Weiliang, CAI Jingjing. Inflatable Reentry Technologies Research for Single Launching and Multi-Reentry (SLMR) Space Transporting System[J]. Human Spaceflight, 2011(4): 37-42. (in Chinese)
[16]唐伟, 桂业伟, 王安龄, 等. 充气气囊减速方案的气动设计研究[J]. 宇航学报, 2007, 28(2): 265-268. TANG Wei, GUI Yewei, WANG Anling, et al. Aerodynamic Design for an Inflatable Reentry and Descent Decelerator[J]. Journal of Astronautics, 2007, 28(2): 265-268. (in Chinese)
[17]夏刚, 程文科, 秦子增. 充气式防热罩再入轨道设计[J]. 国防科技大学学报, 2002, 3(24): 7-8. XIA Gang, CHENG Wenke, QIN Zizeng. Re-entry Trajectory Design of Inflatable Thermal Shield[J]. Journal of National University of Defense Technology, 2002, 3(24): 7-8. (in Chinese)
[18]ROE P L. Generalized Formulation of TVD Lax-wendroff Schemes[R]. ICASE, 1984: 84-53.
[19]YOON S, JAMESON A. Lower-upper Symmetric Gauss-sediel Method for the Euler and Navier-Stoker Equation[J]. AIAA Journal, 1988, 26(9): 1025-1026.
[20]PEERY K. Blunt-body Flow Simulations[J]. AIAA Journal, 1988, 29(6): 2904-2910.
The Prediction of Aerodynamic Performance of Inflatable Reentry Vehicle at Various Speeds and Attack Angles
ZHAO Xiaoshun YU Li YANG Xue
Aerodynamic deceleration is one of the key technologies for aerospace vehicles. The inflatable reentry vehicle can increase its payload by reducing the weight of the return system, which has the obvious advantages of light weight, easy package, large drag area, low ballistic coefficient, and small heat generated by hypersonic air. The NASA's Inflatable Reentry Vehicle (IRV-3) is used as an example to study the flow field numerical calculation of different speeds and attack angles, by using finite volume method. Comparing the viscous flow field numerical model result with the inviscid model, result shows that inviscid model in supersonic cases can meet certain accuracy requirements, improving the stability and the calculation efficiency. The aerodynamic performances at different speeds and attack angles are also studied. The results indicate that drag coefficient increases with increased much number and then gradually decreases, which reach a maximum value at 5Ma. When the attack angle changes at small angle, the changes of pitching moment coefficient and lift coefficient are bigger than the drag coefficient. A proper attack angle can reduce the pitching moment coefficient, which improves the stability of inflatable reentry vehicle. The results of this paper have reference value for design and analysis of inflatable reentry vehicles.
inflatable reentry vehicle; aerodynamic performance; CFD; viscosity model; space recovery
V411.3
: A
: 1009-8518(2016)05-0027-10
10.3969/j.issn.1009-8518.2016.05.004
2015-11-02
赵晓舜,男,1990年生,现在南京航空航天大学人机与环境工程专业攻读博士学位。研究方向为航天器的再入、减速。E-mail:zhaoxiaoshun123@126.com。
(编辑:刘颖)
(College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)
国家自然科学基金(11172137)资助项目;江苏高校优势学科建设工程资助项目(PAPD)
