半刚性机械展开式气动减速技术机构特征研究

张鹏尚明友李旭东白良浩侯向阳

（1 中国空间技术研究院载人航天总体部，北京 100094）

（2 南京航空航天大学飞行器先进设计技术国防重点学科实验室，南京 210016）

半刚性机械展开式气动减速技术机构特征研究

张鹏1尚明友1李旭东2白良浩1侯向阳1

（1 中国空间技术研究院载人航天总体部，北京 100094）

（2 南京航空航天大学飞行器先进设计技术国防重点学科实验室，南京 210016）

半刚性机械展开式气动减速技术作为可展开气动减速技术的一种，其气动面结构区别于柔性充气式展开技术的气囊结构，它主要是一个由辐条、连接杆、头锥及主体等部件构成的连杆机构系统。连杆机构系统是半刚性机械展开式气动减速技术重要组成部分，对其开展特征研究是有效利用火箭整流罩空间、保证气动面构型稳定的基础。文章首先根据半刚性机械展开式气动减速技术结构特点及受力情况，建立了连杆机构几何模型和力学模型；然后采用数学解析法半定量分析和有限元法验证的手段，从几何参数、收拢包络、机构变形、系统刚度等方面对机构特征进行了分析与比较。通过研究，得出了最小收拢包络条件及最小变形条件；确定了变形最小、刚度最好、收拢包络最小的连杆机构状态；给出了连杆机构几何参数选择建议。文章研究内容及结论为进行半刚性机械展开式气动减速技术工程实施及机构优化设计提供了参考。

机械式展开 机构特征 几何参数 收拢包络 机构变形 系统刚度 航天器气动减速

0 引言

传统的再/进入航天器气动构型都是刚性固定式结构，受运载火箭整流罩包络约束，极大地限制了航天器气动构型尺寸、质量及弹道系数，从而大大降低了航天器载荷运输能力[1]。可展开气动减速技术以其独特的结构形式能够实现气动面发射时收拢、再/进入时展开等功能，从而彻底克服了传统再/进入航天器受火箭包络约束的缺点[1-2]。

美国NASA提出的半刚性机械展开式气动减速技术（Semi-rigid Mechanical Deployable Aerodynamic Deceleration Technology，SMDADT）作为可展开气动减速技术的一种，其气动面结构区别于柔性充气式展开技术的气囊结构[3-10]，它主要是一个由辐条、连接杆、头锥及主体等部件构成的连杆机构系统。该系统通过电机或制动器驱动头锥和主体发生轴向相对运动，从而带动辐条和连接杆运动，最终实现气动面收拢与展开[11-12]，如图1所示。连杆机构各组成部分的比例关系及连接点位置等几何参数将直接影响到SMDADT的收展程度，从而关系到该技术克服火箭整流罩包络约束的能力。

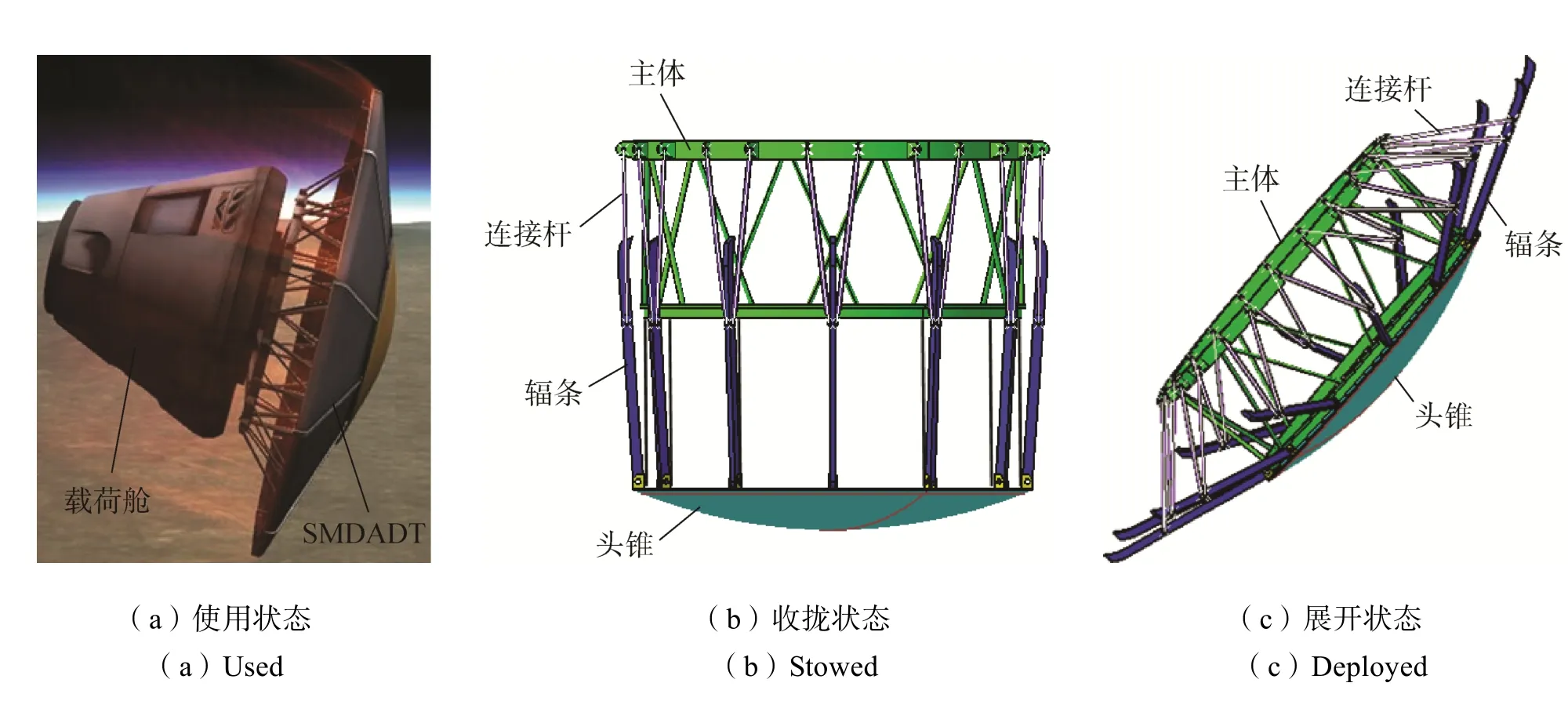
图1 SMDADT结构形式Fig.1 Structure configurations of SMDADT

连杆机构系统除了实现SMDADT收展功能外，还起到在再/进入过程中保持气动面构型稳定的作用[1]。机构几何参数的变化将影响系统的承载能力，系统变形越大、刚度越弱，气动面构型稳定性就越差，从而将导致热流密度分布发生变化，严重时甚至改变气动面钝度比，偏离设计状态，最终致使任务失败[1,13-14]。

因此，进行SMDADT连杆机构几何参数、收展状态包络尺寸及系统承载能力等特征研究，是有效利用火箭整流罩空间，提高运载能力，保证气动面构型稳定的基础。目前，国内对 SMDADT研究尚无公开报道，美国NASA对SMDADT研究也主要是聚焦在总体方案、功能应用、防热材料研制和气动特性等方面[11-13,15-19]，并未就连杆机构特征进行专门研究。为此，本文首先依据SMDADT结构特点及受力情况，建立连杆机构系统几何模型和力学模型；然后针对工程上关心的两种特殊状态（最小收拢包络状态、辐条最小变形状态），采用数学解析法半定量分析归纳和有限元法验证的手段，不失一般性地研究连杆机构几何参数变化对系统刚度、系统变形、收拢包络的影响；最后确定变形最小、刚度最好、收拢包络最小的连杆机构状态并给出参数选择建议。本文研究内容、方法及结论为我国进行SMDADT工程实施及机构优化设计提供理论基础。

1 模型建立与简化

1.1几何模型建立与简化

根据图1所示的SMDADT结构形式及组成，建立了如图2所示的连杆机构轴对称简化模型。图2中辐条（常值），展开状态下气动面半锥角∠COA=α（根据气动特征分析确定，一般为不小于45°的常值），收拢状态下∠COA=θ（为避免收拢状态下出现死点，一般设计为大于0的常值小量）；连杆一端连接于辐条的B点，另一端A点固定且与辐条的O点处于同一直线上。设连接杆的长度为L1，辐条OB的长度为L2、辐条的长度为L3，机构收拢状态下径向包络半径为S、轴向包络为H。

收拢状态下，SMDADT机构径向包络S与轴向包络H分别为：

图2 SMDADT机构原理模型Fig.2 Mechanism Principle Model of SMDADT

1.2 力学模型建立与简化

根据文献[11]提供的SMDADT受力状态，建立了如图3（a）所示的连杆机构受力模型。在不考虑气动剪力τ的情况下，辐条变形可简化成外伸梁的弯曲变形问题，如图3（b）所示。

图3 气动面受力Fig.3 Loaded on aerodynamic area

图3（a）中，q、τ分别为作用在辐条上的气动压力和气动剪力；T为连接杆轴向力，为连接杆轴向力关于O点的力臂；F为连接杆轴向力T沿向分力；P为作用在刚性头锥上沿向气动力合力。

连接杆压缩变形Δ为：

式中 K为连接杆抗压刚度（常值）。

则连杆机构系统总变形u为：

2 最小收拢包络条件下机构特征分析

2.1 最小收拢包络条件

在工程上，一般希望发射包络最小。由式（1）知，S为一定值。由式（2）知，要想H最小，则H=H2≥H1，即：

考虑到展开状态下的几何关系，只有当，式（11）才成立；只有当L1≥L2sinα时，△OAB才存在。

因此，当辐条与连接杆长度关系满足式（12）式时，SMDADT收拢状态包络最小，且S=Lθ，H=L。

2.2 当时机构特征

为不失一般性，图4为L3取三种典型值时机构展开状态的几何关系。通过计算分析可知：

图4 L3取三种典型值时几何关系Fig.4 Geometric relations at three typical values of L3

随着L3的不断增大，先减小后增大（如图4所示），则由式（5）知，连接杆压缩变形Δ先减小后增大；随着L3的不断增大，由式（7）知，辐条变形δ逐渐增大；虽然连接杆压缩变形Δ有减小的阶段，但其减小幅度远小于辐条变形δ增大的幅度，所以整个机构的变形u随着L3的增大而明显增加，如图5所示，当时，连杆机构系统的变形最小；

随着L3的不断增大，整个机构的一阶频率逐渐减小。当时，连杆机构系统的刚度最好，如图6所示。

图5 L3取三种典型值时机构变形uFig.5 Mechanism deformation u at three typical values of L3

图6 L3取三种典型值时机构基频Fig.6 Mechanism fundamental frequency at three typical values of L3

2.3当L3为不小于的某一定值，时机构特征

为不失一般性，对L3分段分析。图7是L3为两种不同状态、L1取不同值时机构展开状态的几何关系，通过计算分析可知：

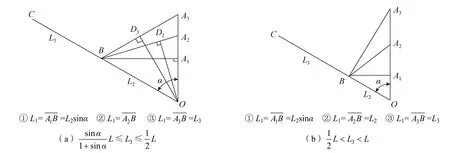
图7 L1取不同值时几何关系Fig.7 Geometric relations at different values of L1

图8 L1取不同值时机构变形uFig.8 Mechanism deformation u at different values of L1

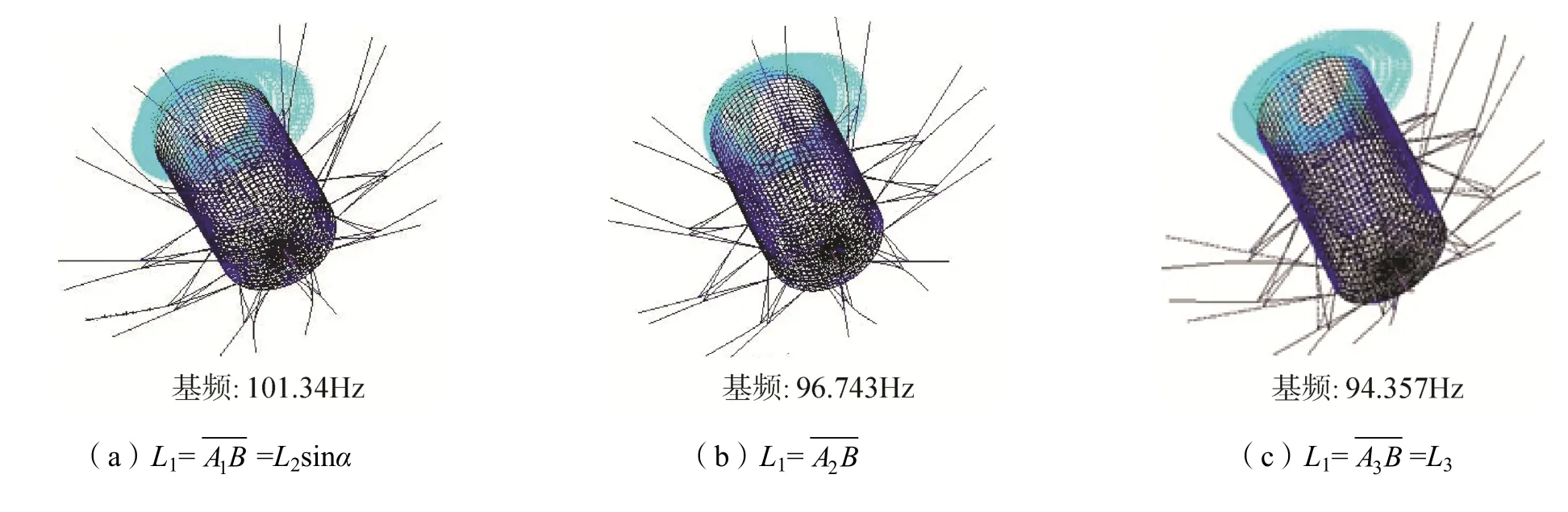
图9 L1取不同值时机构基频Fig.9 Mechanism fundamental frequency at different values of L1

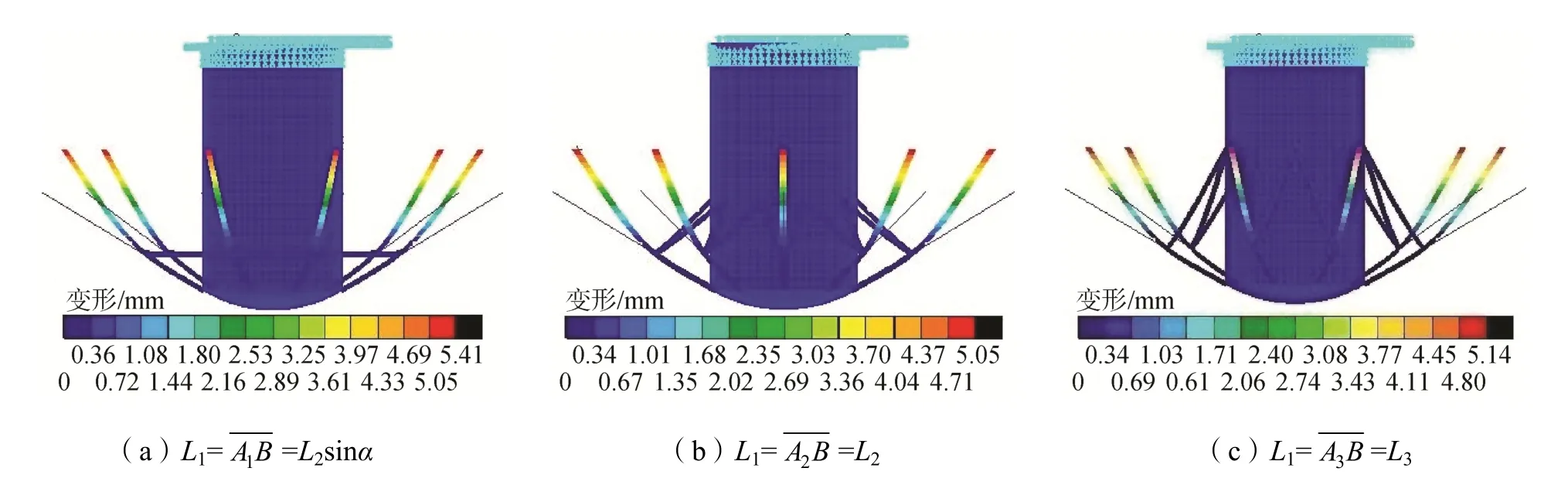
图10 L1取三种典型值时机构变形uFig.10 Mechanism deformation u at three typical values of L1

图11 L1取三种典型值时机构基频Fig.11 Mechanism fundamental frequency at three typical values of L1

3 辐条最小变形条件下机构特征分析

3.1 辐条最小变形条件

为便于描述，令L2/L=a，当a从1减小至0.845 3时，段绕度逐渐减小，段绕度y2max逐渐增大。因减小幅度大于y2max增大幅度，所以，如图12（a）、（b）；

图12 辐条变形Fig.12 Deformation of ribs

由此可见，当L2/L=0.673 5时，段最大绕度等于段C点绕度，此时辐条变形δ最小。

3.2 当L2/L=0.673 5时机构特征

当L2/L=0.673 5时，因α≥45°，此时。即：当辐条变形δ取最小值时，连杆机构系统不满足式（14）给出的SMDADT最小收拢包络条件。根据式（2），此时轴向包络H=H1=L1+L2，且当L1=L2sinα，轴向包络最小，如图13所示。

根据第2节分析方法及相关结论可知，当L2/L=0.673 5时，整个机构的变形u是随着L1的增大，先减小后增大，当L1=L2时，连杆机构系统的变形最小；当L2/L=0.673 5时，整个机构的系统刚度是随着L1的增大逐渐减小，当L1=L2sinα时，连杆机构系统刚度最好，如图14所示；

4 连杆机构系统几何参数选择

根据以上分析可知，SMDADT连杆机构系统几何参数主要涉及B点位置（即L2、L3的比例关系）和连接杆L1长度。

4.1 B点位置选择

从工程应用而言，在进行SMDADT结构总体设计时，若火箭整流罩包络为强约束，建议B点选择在处作为初始设计状态。这是因为 B点选择在该处时，整个连杆机构系统才具备包络最小、刚度最好、变形最小的条件；若火箭整流罩包络为弱约束，建议B点选择在L2/L=0.673 5处作为初始设计状态。这是因为B点选择在该处时，辐条变形最小，气动面构型稳定性较好。

图13 L1取不同值时几何关系Fig.13 Geometric relations at different values of L1

图14 L1取三种典型值时机构基频Fig.14 Mechanism fundamental frequency at three typical values of L1

4.2 连接杆长度选择

通过本文分析，当L1等于L2sinα或L2两种状态时，整个机构特性相对其他状态更好。

对于L1=L2状态而言，从图3（a）明显看出，在气动力作用下，连接杆轴向力T在A点处存在沿向分力F，分力F使SMDADT结构存在逆向收拢的风险（即：结构展开后，在气动力作用下二次收拢）。控制该风险的措施一般有三种：第一是设计锁紧机构，但这种方式会增加系统复杂程度；第二是增加头锥和主体间轴向运动阻力，但这种方式也同时增加了 SMDADT结构在展开过程中的驱动力；第三是适当增加刚性头锥直径，使头锥受到的气动力沿向合力 P大于连接杆分力 F，从而始终保证展开状态下O点与A点间距不变。因SMDADT收拢状态下的径向包络是由头锥尺寸和连杆机构半径S共同决定的，所以第三种措施会增加SMDADT收拢径向包络。

对于L1=L2sinα状态来说，连接杆轴向力T在A点处不存在沿向分力F，不会出现使SMDADT结构逆向收拢的情况。虽然此时连接杆压缩变形Δ大于L1=L2状态下的压缩变形Δ，但可以通过优化连接杆截面参数补偿。比起三种控制逆向收拢风险措施来，优化连接杆截面参数更易实现，代价更易接受。

因此，在进行SMDADT结构总体设计时，建议选择L1=L2sinα作为初始设计状态。

5 结束语

本文采用数学解析法半定量分析归纳和有限元法验证的手段，研究了在最小收拢包络及辐条最小变形两种特殊状态下SMDADT连杆机构几何参数变化对系统刚度、变形的影响，得出以下结论：

2）SMDADT展开状态辐条受气动力作用变形δ最小条件是：L2/L=0.673 5；且在连杆系统截面参数一定的情况下，当L1=L2sinα时，整个机构的刚度最好；当L1=L2时，整个机构变形u最小。

将本文研究内容，不失一般性地推广，得到如下基本规律：

通过分析给出SMDADT总体结构设计建议如下：若火箭整流罩包络为设计强约束，则连杆系统应选择作为初始设计状态；若火箭整流罩包络为设计弱约束，则连杆系统应选择L2/L=0.673 5、L1=L2sinα作为初始设计状态。

References)

[1]张鹏, 李旭东, 白良浩, 等. 半刚性机械展开式气动减速技术述评[J]. 航天返回与遥感, 2016, 37(1): 1-9. ZHANG Peng, LI Xudong, BAI Lianghao, et al. Review of Semi-rigid Mechanical Deployable Aerodynamic Deceleration Technology [J]. Spacecraft Recovery & Remote Sensing, 2016, 37(1): 1-9. (in Chinese)

[2]李旭东, 张鹏, 尚明友, 等. 基于金星探测机械展开式进入飞行器技术述评[J]. 航天返回与遥感, 2015, 36(2): 1-8. LI Xudong, ZHANG Peng, SHANG Mingyou, et al. Review of Venus Explorer Mission Using Mechanically-deployed En-try Decelerator[J]. Spacecraft Recovery & Remote Sensing, 2015, 36(2): 1-8. (in Chinese)

[3]JOSEPH A D C, CHEATWOOD F M, BRUCE III W E, et al. Advanced High-temperature Flexible TPS for Inflatable Aerodynamic Decelerators[C]//21st AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Dublin, Ireland, AIAA 2011-2510, 2011.

[4]ETHIRAJ V. Enabling Venus and Outer-planet In-Situ Science Missions with Deployables[R]. International Planetary Probe Workshop, Portsmouth, 2011.

[5]高艺航, 贺卫亮. 充气式返回舱气动热特性研究[J]. 航天返回与遥感, 2014, 35(4): 17-25. GAO Yihang, HE Weiliang. Research on Aerodynamic Heating Characteristics of Inflatable Reentry Decelerator[J]. Spacecraft Recovery & Remote Sensing, 2014, 35(4): 17-25. (in Chinese)

[6]荣成成, 左光, 陈冲, 等. 充气式再入航天器总体方案及关键技术初探[J]. 航天返回与遥感, 2015, 36(1): 16-23. RONG Chengcheng, ZUO Guang, CHEN Chong, et al. A Study of General Scheme and Key Technologies of Inflatable Re-entry Vehicle[J]. Spacecraft Recovery & Remote Sensing, 2015, 36(1): 16-23. (in Chinese)

[7]夏刚, 程文科, 秦子增. 充气式再入飞行器柔性热防护系统的发展状况[J]. 宇航材料工艺, 2003, 33(6): 1-6. XIA Gang, CHENG Wenke, QIN Zizeng. Development of Flexible Thermal Protection System for Inflatable Re-entry Ve-hicles[J]. Aerospace Materials & Technology, 2003, 33(6): 1-6. (in Chinese)

[8]卫剑征, 谭惠丰, 王伟志, 等. 充气式再入减速器研究最新进展[J]. 宇航学报, 2013, 34(7): 881-890. WEI Jianzheng, TAN Huifeng, WANG Weizhi, et al. New Trends in Inflatable Re-entry Aeroshell[J]. Journal of Astronau-tics, 2013, 34(7): 881-890.(in Chinese)

[9]黄明星, 王伟志. 某型充气式再入减速热防护结构优化分析[J]. 航天返回与遥感, 2016, 37(1): 22-31. HUANG Mingxing, WANG Weizhi. Optimization on a Flexible Thermal Protection Structure of Inflatable Reentry System[J]. Spacecraft Recovery & Remote Sensing, 2016, 37(1): 22-31. (in Chinese)

[10]王伟志. 充气展开式新型空间回收技术展望[J]. 航天返回与遥感, 2004, 25(1): 1-5. WANG Weizhi. Forecast of the New Type Inflatable Deployment Space Recovery Technology[J]. Spacecraft Recovery & Remote Sensing, 2004, 25(1): 1-5. (in Chinese)

[11]BRYAN Y, DINESH P, CARL K, et al. Structures and Mechanisms Design Concepts For Adaptive Deployable Entry Placement Technology[C]//Aerodynamic Decelerator Systems Technology Conferences, Florida, AIAA 2013-1369, 2013.

[12]ETHIRAJ V, JAMES A, IAN F, et al. Adaptive Deployable Entry and Placement Technology(ADEPT): A Feasibility Study for Human Missions to Mars[C]//21st AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Dublin, Ireland, AIAA 2011-2608, 2011.

[13]BRANDON S, ETHIRAJ V, DINESH P, et al. Venus in Situ Explorer Mission Design Using a Mechanically Deployed Aerodynamic Decelerator[R]. IEEE Aerospace Conference, Big Sky, 2013.

[14]张章, 黄伟, 唐明章, 等. 空间再入飞行器热气动弹性数值研究进展[J]. 航天返回与遥感, 2016, 37(1): 10-21. ZHANG Zhang, HUANG Wei, TANG Mingzhang, et al. A Review of Aerothermoelastic Numerical Research on Space Reentry Vehicles[J]. Spacecraft Recovery & Remote Sensing, 2016, 37(1): 10-21. (in Chinese)

[15]ERIC S, MICHAEL B, ETHIRAJ V, et al. Investigation of Transonic Wake Dynamics for Mechanically Deployable Entry Systems[R]. IEEE Aerospace Conference, Big Sky, 2012.

[16]SARAG J S, HARISH S, MICHAEL J G, et al. Trajectory Optimization for Adaptive Deployable Entry and Placement Technology (ADEPT) [C]//AIAA/AAS Astrodynamics Specialist Conferences, San Diego, AIAA 2014-4139, 2014.

[17]BRANDON P S, BRYAN C Y, ETHIRAJ V. Progress in Payload Separation Risk Mitigation for a Deployable Venus Heat Shield[C]//Aerodynamic Decelerator Systems Technology Conferences, Florida, AIAA 2013-1371, 2013.

[18]WERCINSKI P, VENKATAPATHY E. Enabling Venus In-situ Science-deployable Entry System Technology, Adaptive Deployable Entry and Placement Technology (ADEPT): A Technology Development Project Funded by Game Changing Development Program of the Space Technology Program[R]. IEEE Aerospace Conference, Big Sky, 2012.

[19]ETHIRAJ V. Adaptive Deployable Entry and Placement Technology (ADEPT): A Technology Development Project Funded by Game Changing Development Program of the Office of Chief Technologist[R]. VEXAG Meeting, San Francesco, 2013.

[20]魏兆正. 材料力学[M]. 大连: 大连理工大学出版社, 1994: 123-149. WEI Zhaozheng. Materials Mechanics[M]. Dalian: Dalian University of Technology Publishing House, 1994: 123-149. (in Chinese)

Research on Mechanism Characteristics of Semi-rigid Mechanical Deployable Aerodynamic Deceleration Technology

ZHANG Peng1SHANG Mingyou1LI Xudong2BAI Lianghao1HOU Xiangyang1

（1 Institute of Manned Space System Engineering, China Academy of Space Technology, Beijing 100094, China）
（2 Ministerial Key Discipline Laboratory of Advanced Design Technology of Aircraft, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China）

As a kind of deployable aerodynamic deceleration technology, the aerodynamic structure of the semi-rigid mechanical deployable aerodynamic deceleration technology is different from the air-bag structure of the flexible inflatable aerodynamic deceleration technology, and it is a linkage mechanism which is made up of ribs, struts, nose and main body. The linkage mechanism is an important part of the semi-rigid mechanical deployable aerodynamic deceleration technology, the mechanism characteristics research is fundamental to efficiently use rocket fairing space and ensure aerodynamic surface configuration stable. Firstly, the paper establishes a linkage mechanism geometry and mechanics models according to the structural features and loaded state of the semi-rigid mechanical deployable aerodynamic deceleration technology. Secondly, using means of mathematics analytical method semi-quantitative analysis and finite element method verification, it analyzes and compares the mechanism characteristics from four aspects, including geometric parameters, folded envelope, structural deformation and system stiffness. Through research, the paper obtains the minimum foldedenvelope conditions and minimum deformation conditions, determines the linkage mechanism states of the minimum deformation, best stiffness and smallest folded envelope, and gives advice for the geometric parameter selection of linkage mechanism. The procedure and the conclusions of the research provide a theoretical basis for the project implementation and mechanism optimization design of the semi-rigid mechanical deployable aerodynamic deceleration technology.

mechanical deployment; mechanism characteristics; geometric parameters; folded envelope; structural deformation; system stiffness; spacecraft aerodynamic deceleration

V423.6

: A

: 1009-8518(2016)05-0037-012

10.3969/j.issn.1009-8518.2016.05.005

张鹏，男，1982年生，2011年获华中科技大学固体力学专业博士学位。研究方向为航天器系统设计、气动设计及总装集成设计。E-mail：zhangpeng01061014@163.com。

（编辑：刘颖）

2016-02-10

国家重大科技专项工程