一种伞衣织物透气性快速预测算法
2016-02-23宁雷鸣张红英童明波
宁雷鸣 张红英 童明波
(南京航空航天大学航空宇航学院,南京 210016)
一种伞衣织物透气性快速预测算法
宁雷鸣 张红英 童明波
(南京航空航天大学航空宇航学院,南京 210016)
伞衣织物透气性是决定降落伞气动特性的重要因素,因此快速而准确地预测伞衣织物透气性将能够有效减少透气性试验次数并提高降落伞仿真计算可靠性。文章根据降落伞伞衣织物材料的结构特点,基于多孔介质透气性理论提出了一种伞衣织物透气性预测算法,该算法可以在缺乏透气量试验数据的情况下,仅根据伞衣织物厚度和标准透气量大小快速计算得到该伞衣的透气性曲线(压差-透气量曲线)。应用该算法对多种国际上常见伞衣织物材料的透气性进行了计算,并给出了相应透气性参数预测结果。为进一步分析该预测算法的可靠性和适用范围,基于任意拉格朗日-欧拉方法建立了织物透气性仿真试验流固耦合模型,将上述预测得到的织物透气性参数用于仿真试验中,并将预测结果与试验数据进行了对比分析。结果表明,文章提出的算法对常见伞衣织物在中低压差下的透气量具有较好的预测精度,能够方便快速地预测各类不同伞衣织物在降落伞工作过程中的透气性能,可被用于降落伞的工程设计、性能计算、仿真分析等工作之中。
伞衣织物 透气性 任意拉格朗日-欧拉方法 流固耦合 降落伞
0 引言
降落伞作为一种高效的气动减速器在航天器再入返回、空降空投、航弹稳定和各类飞行器及部件回收等方面有着广泛的应用。降落伞的性能主要取决于其自身的气动特性,而降落伞的伞衣织物透气性是决定降落伞气动特性的重要因素,它对降落伞的充气时间、开伞动载、稳定性和稳降速度等关键性能指标都有显著的影响[1-3]。例如伞衣透气性过大将使降落伞无法充满,而透气性过小将使降落伞稳定性不足或开伞动载过大。因此,掌握各类降落伞织物的透气性规律对于降落伞的设计选材、改型优化、性能验证等工作具有重要意义。
透气性作为织物材料的一种物理性能一般是由纤维原料、组织结构及整理加工等诸多因素决定的[4]。由于不同的织物材料具有不同的透气性能,因此对于一种具体的织物材料通常给出某一标准试验压差下的透气量(即单位时间内流经织物单位面积的空气量)作为该织物透气性的表征和度量。但是透气量的大小取决于具体的试验压差,仅标准压差下的透气量数据并不能反映织物透气性能的全貌。尤其对于降落伞来说,其充气过程经历较大的压差变化,所以为了完整表征并预测降落伞织物的透气性能,需要掌握织物在一定压差范围内的透气量变化情况,即透气量方程[5]。
伞衣织物的透气量方程大多通过大量的试验并藉由多组压差-透气量数据拟合得到[6-9],相关的预测理论研究则较少。近年来,随着基于任意拉格朗日-欧拉(Arbitrary Lagrangian-Eulerian,ALE)方法的降落伞流固耦合仿真计算技术的成熟与普及,为了能在仿真中考虑实际织物材料的透气性效应从而得到可靠的计算结果,研究人员需要能够快速有效地得到各种伞衣织物的透气量方程。国外最早由Goglia等通过大量试验数据的统计分析揭示了伞衣织物透气量方程和多孔介质渗流理论中的Ergun公式具有一致的形式[10];文献[11]中Jason Wang等人基于Ergun公式给出了一种利用织物的透气性曲线(即压差-透气量关系曲线)进行双点估计反算得到透气量方程系数的方法,并在LS-DYNA中建立ALE流固耦合模型对估算得到的系数进行了验证;随后国内贾贺基于该方法进行了进一步的计算和验证[12]。但该方法本质上是利用多组透气量数据进行曲线拟合,需要事先对伞衣织物进行多组透气量试验才能进行可靠的预测,而目前多数伞衣织物只提供了标准压差下的透气量作为性能参数,因此拟合法就显出其局限性。
本研究首先根据伞衣织物的结构特点,基于Ergun透气性理论进行了推导和分析,给出了一种适于降落伞织物的透气性预测算法,该算法可以在缺乏试验数据时仅利用标准压差下的透气量信息来预测织物透气量方程;然后使用该算法对多种国内外常见伞衣织物材料的透气量方程进行了预测并与相应试验数据进行了比较分析;最后将预测结果应用于数值模拟中,基于ALE方法进行了织物透气性流固耦合仿真试验,进一步讨论了该预测算法在实际应用中的可靠性和适应性。
1 织物透气性理论简介
织物的透气性一般以透气量来作为具体的表征和量度。透气量是指在一定的试验压差下单位时间内流经织物单位面积的空气量,等价于该压差下气流垂直通过织物的速率,即透气率,一般以 L/(m2s)或mm/s为单位[13]。
织物透气量的大小取决于具体的试验压差,但两者并非简单的线性关系。大量研究和试验表明[6-7,10],织物可以被视作一种多孔介质材料,其透气量方程和多孔介质渗流理论中的Forchheimer[14]公式具有一致的形式,即透气量与压差之间满足如下二次多项式关系:

式中 ΔP为多孔介质两边的压强差;L为介质厚度;V为透气量;α和β为取决于具体多孔介质几何特性的待定系数。式(1)在宏观尺度上给出了织物透气量随压差的变化关系,公式左端表征沿介质厚度方向的压强变化梯度,右端两项分别为表征粘性耗散的层流分量和表征动能损失的湍流分量,所以系数α和β又分别称为粘性系数和惯性系数。
Ergun基于Forchheimer公式的大量试验分析表明,气流在流经透气性介质后的压强损失与来流速度、气体属性(密度和动粘度)以及介质自身几何特性间存在如下经验关系[15]:
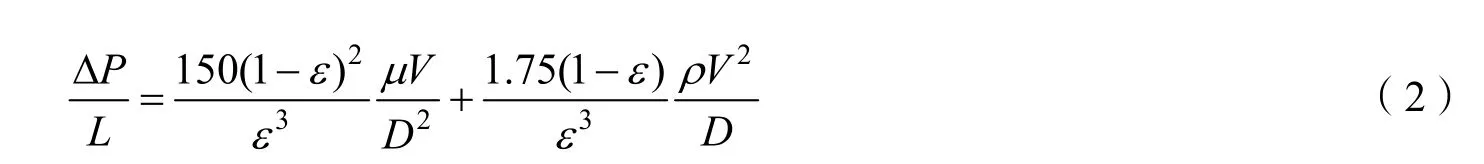
式中 μ为空气动粘度;ρ为空气密度;D为表征透气性介质中孔隙尺寸的特征长度;ε为多孔介质相对透气量,即多孔介质中空隙所占体积与介质总体积的比值。此式即为透气性理论计算中最广为使用的Ergun公式。
Ergun公式中给出了Forchheimer公式中粘性系数和惯性系数的一般表达式如下(以下统称为Ergun透气性系数):

由于Ergun公式右端项同时考虑了低流速时占主导的层流分量和高流速时占主导的湍流分量,具有较大的适用范围,因此被广泛地应用于各类降落伞数值计算中以考虑伞衣织物透气性对流场造成的影响。
2 伞衣织物的简化透气性预测方法
在使用 Ergun公式作为伞衣织物透气量方程进行透气性预测时,需要事先计算出式(3)中的两个Ergun系数。现有的方法[11-12]需要通过对多组不同压差下的透气量数据进行曲线拟合来得到这两个系数。而在实际进行织物透气量试验时,为了使各种织物间的透气量数值具有可比性,各国都有相应标准对不同用途织物的透气量试验压差作出明确的规定[1],例如我国规定降落伞织物的透气量标准试验压差约为50Pa,因此在各类伞衣织物的性能参数中往往只有这一标准压差下的透气量数据,而非多组不同压差下的透气量数据。此时拟合法将因数据量不足而不再适用。
观察式(3)可以发现,在Ergun理论中两个Ergun透气性系数均为特征长度D和相对透气量ε的函数,即织物的透气性能将由织物结构几何特征量D和ε确定。其中特征长度D在Ergun公式中的物理意义为由球状粒子组成的多孔介质层中粒子的平均直径大小,它的计算式为:

式中 St为介质层浸润面积(含孔隙内壁面积);Vt为介质层总体积(不含介质中的孔隙体积),其计算式为:

式中 A为介质层横截面积。
若将伞衣织物等效为孔隙均匀分布的多孔介质,则其孔隙内壁面积为等效孔隙周长与孔隙深度(即织物厚度)之积,由于降落伞伞衣一般为厚度较小(一般在0.1mm左右[4])的密实织物,因此其等效孔隙尺寸及孔隙深度相对于伞衣面积来说都很小,远小于一般降落伞的平铺尺寸。因此与织物平铺面积相比,织物内部纱线间的孔隙内壁面积大小可以忽略,从而将织物平铺面积近似作为特征长度计算式(4)中的浸润面积,即:

联立式(4)~(6)可以得到织物特征长度D的近似计算式为:

代入式(3)中可以得到简化后的Ergun系数为:

若进一步将特征长度表达式代入Ergun公式中,并结合已知的标准试验条件下的透气量数据,可以得到相对透气量ε的计算式如下:
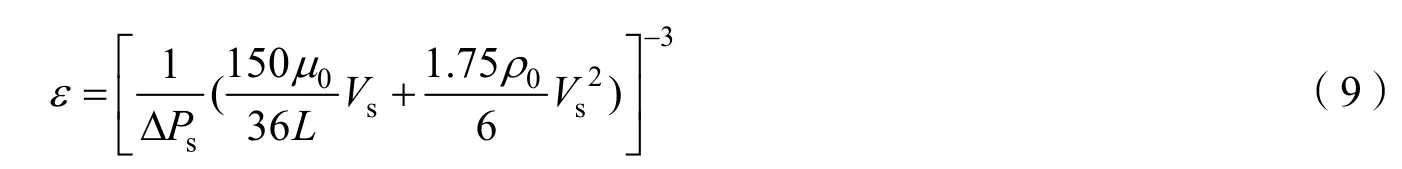
式中0ρ和0μ为纺织品试验用标准大气[13]中规定的空气密度和动粘度;ΔsP为标准试验压差;Vs为该压差下的透气量。该式可利用多数情况下已知的标准透气量数据计算出织物相对透气量ε,结合式(8)即可计算得到Ergun公式中的粘性系数和惯性系数。
为验证本文提出的简化透气性预测模型的有效性,下面分别选取三种美军常用的伞衣织物材料[8-9]和三种国内常见的伞衣织物材料[5,16]进行透气性预测分析。各织物材料的已知参数如表1所示。
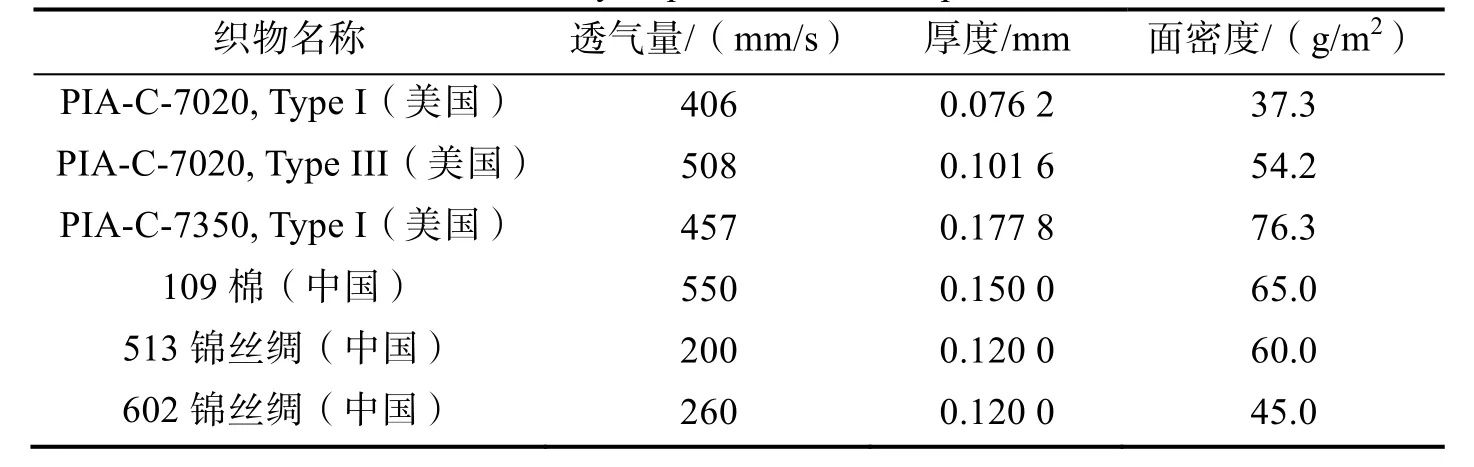
表1 伞衣织物材料的主要参数Tab.1 Summary of parachute fabric specifications
首先以美军降落伞常用的PIA-C-7020,Type III材料为例说明简化模型的计算过程。美军标规定的降落伞织物标准试验压差ΔsP=125Pa[8],该标准压差下PIA-C-7020,Type III材料的透气量Vs≈508mm/s,利用式(9)计算得相对透气量为0.155,再由式(8)计算得到该材料的粘性系数和惯性系数如下:

该结果代入式(1)中即为预测得到的透气量方程。
本文预测得到的Ergun透气性系数与文献[11]中的预测结果以及两组试验数据[8-9]最小二乘拟合结果的对比情况如表2所示。
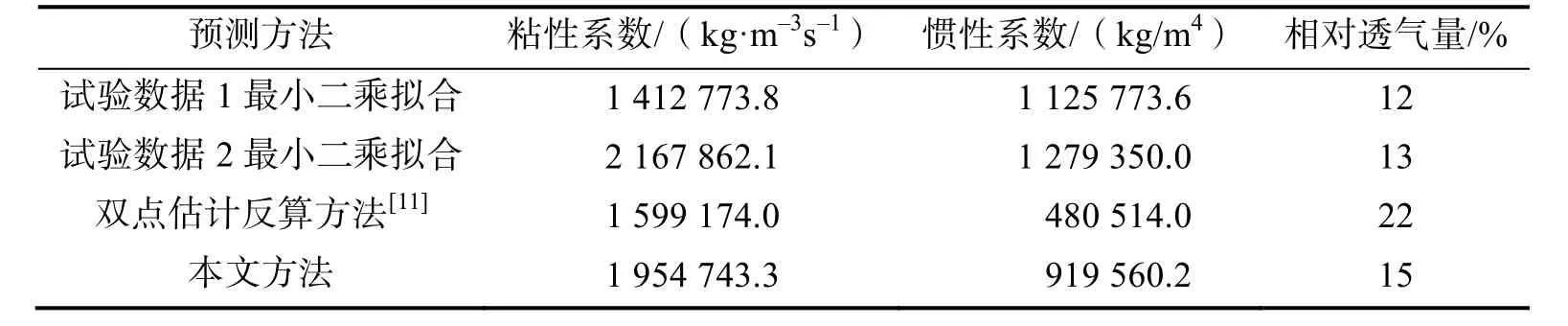
表2 模型预测结果与试验数据拟合结果的对比Tab.2 Comparison between model predictions and test data fitting results
为了更直观地比较各预测结果,表2中同时给出了预测得到的织物相对透气量ε,其计算式为:

预测结果对应的理论透气性曲线与试验数据的对比情况如图1所示。

图1 PIA-C-7020 type III透气性曲线预测结果与试验结果对比Fig.1 Comparison of PIA-C-7020 type III porosity curve predictions and test data
结合表2和图1可以看出:两组试验数据的差异表明即使是对于同一种织物,其透气性并不是完全确定的,而是受加工工艺和外部条件的影响在一定范围内波动[4],但两次试验都表明该织物的相对透气量为12%左右;本文简化模型的理论预测结果整体上与两组试验数据都较为接近,但预测的相对透气量略大于两组试验结果,因此可以看出随着压差的增大预测的透气量曲线有增长过快的趋势,但在 800Pa的压差程内能够较为准确地预测该织物的透气性能;JASON WANG双点估计反算方法的预测结果在低压差下与试验数据较为接近,但当压差在300Pa以上时,预测的透气量明显偏大,这点从其相对透气量的预测结果上也可看出。
表3中给出了本文简化模型对表1中各伞衣织物Ergun系数的理论预测结果。
表3 各伞衣织物Ergun透气性系数预测结果Tab.3 The predicted Ergun porosity parameters of parachute fabrics
3 织物透气性试验仿真分析
以上基于Ergun公式的透气性理论预测,以织物结构几何特征和孔隙尺寸不发生改变为前提,即不考虑织物材料自身的弹性变形。而对于实际的降落伞织物来说,当来流动压较大时织物将在内应力作用下发生明显的弹性拉伸,表面积及孔隙体积都将随之发生变化[9]。为进一步考察本文预测模型在考虑实际织物变形时的适用性,基于ALE方法建立了织物透气性仿真试验有限元模型,将表3中的理论预测结果用于仿真试验中进行计算分析。
3.1有限元模型
一般织物透气性测试仪工作原理如图2所示。

图2 织物透气性测试仪工作原理示意Fig.2 Schematic of fabric permeability tester
织物的一面为大气压,另一面为通过仪器自动控制抽风机所得到压力较低的低压气室,织物通过压头被紧密固定在低压气室入口。在压差 ΔP= P0-P1的作用下织物将逐渐发生变形直至达到稳定状态,此时气流通过织物在管道内形成的平均流速V,即为该压差下织物的透气量大小。
织物在压差作用下受力变形的过程是一个多孔介质流固耦合过程,因此可以使用显式有限元求解器LS-DYNA中的 ALE方法[11-12,17]对整个过程进行仿真计算。
基于ALE方法进行流固耦合仿真计算时,仿真模型中使用拉格朗日方法描述的结构单元和使用欧拉方法描述的流体单元需要分别进行建模,并以网格重叠的方式获得整体流固耦合模型。为了使仿真计算模型与实际透气性测试试验设置尽可能接近,本文仿真计算所使用的有限元模型基本组成如图3所示。
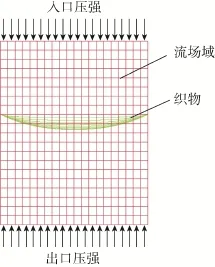
图3 织物透气性仿真计算有限元模型Fig.3 Finite element model of fabric permeability simulation
图3中织物定义为Belytschko-Tsay薄膜元算法描述的织物材料,并根据实际织物的厚度、密度和断裂强度进行材料参数设置,织物外边缘节点设为固定约束。织物两面的流场域采用六面体单元进行网格划分,并定义为满足理想气体状态方程的空气,同时根据纺织品试验用标准大气[13],设置 ρ= 1.18 kg/m3,。流场单元上下表面分别加载大气压和形成所需压差对应的内压,流场单元四周设为物面边界条件以模拟管道流动。织物在一定压差下的透气量通过统计最终流动稳定时流场出口处的平均流速来确定。流场和织物交界面的耦合力使用LS-DYNA中的罚函数方式进行计算,并在耦合选项中定义织物所在的单元为拉格朗日多孔壳单元。由于LS-DYNA求解器中使用Ergun公式来计算多孔介质的附加耦合力,因此可以直接利用表3中Ergun系数预测结果作为耦合设置参数来计算织物透气性的影响。
3.2 试验数据与仿真结果对比分析
图4~9给出了6种伞衣织物的仿真计算结果与表3中的理论预测结果以及透气性试验结果的对比情况。从6种伞衣织物材料的压差—透气量曲线对比情况中可以发现:本文简化模型对各织物的理论预测结果总体上都与透气性试验数据吻合较好,这进一步说明了本文简化预测模型对于伞衣织物的适用性;仿真计算结果在中低压差下较好地预测了各织物真实试验的透气量—压差曲线,但随着压差的增大,仿真计算的透气量结果较之于理论预测的透气量结果开始偏大。
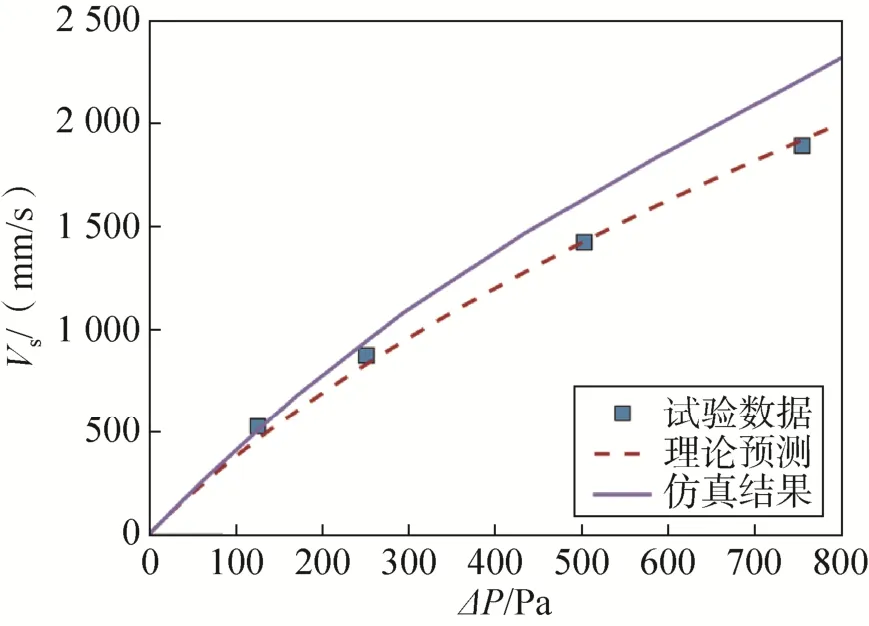
图4 PIA-C-7020 type I透气性曲线结果对比Fig.4 Comparison of PIA-C-7020 type I porosity curves
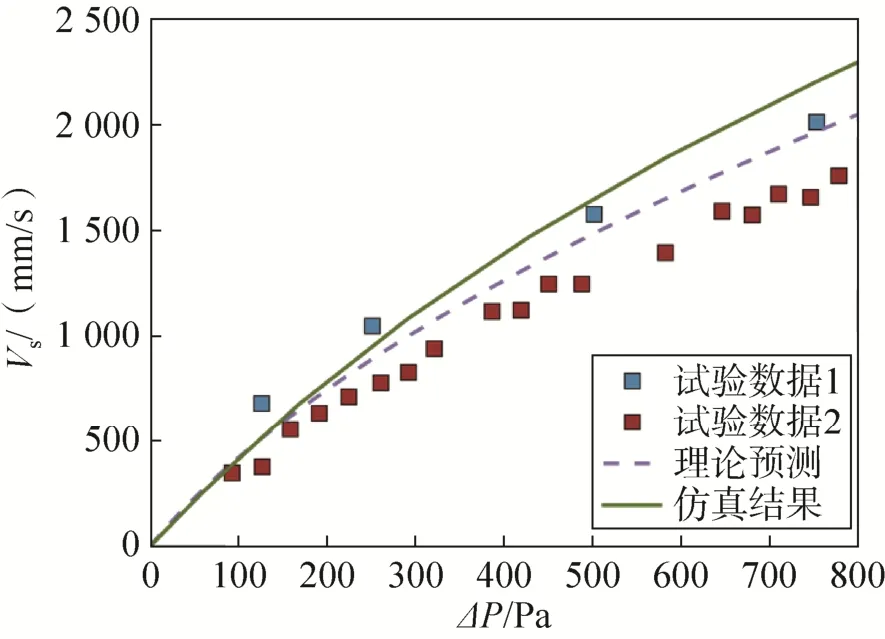
图5 PIA-C-7020 type III透气性曲线结果对比Fig.5 Comparison of PIA-C-7020 type III porosity curves
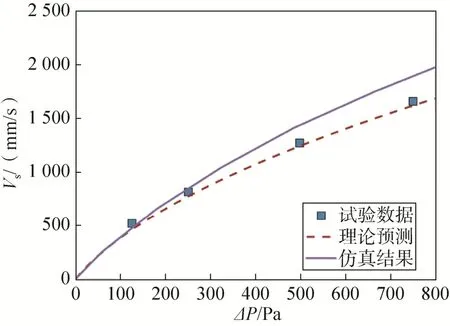
图6 PIA-C-7350 type I透气性曲线结果对比Fig.6 Comparison of PIA-C-7350 type I porosity curves
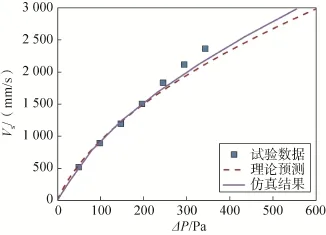
图7 109棉布透气性曲线结果对比Fig.7 Comparison of 109 cotton porosity curves
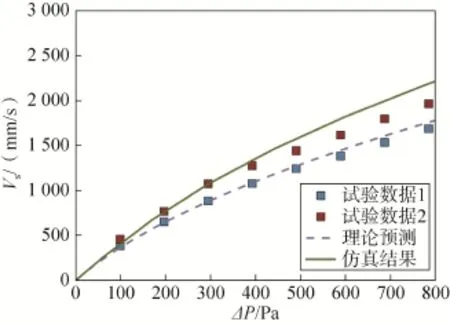
图8 513锦丝绸透气性曲线结果对比Fig.8 Comparison of 513 kam silk porosity curves
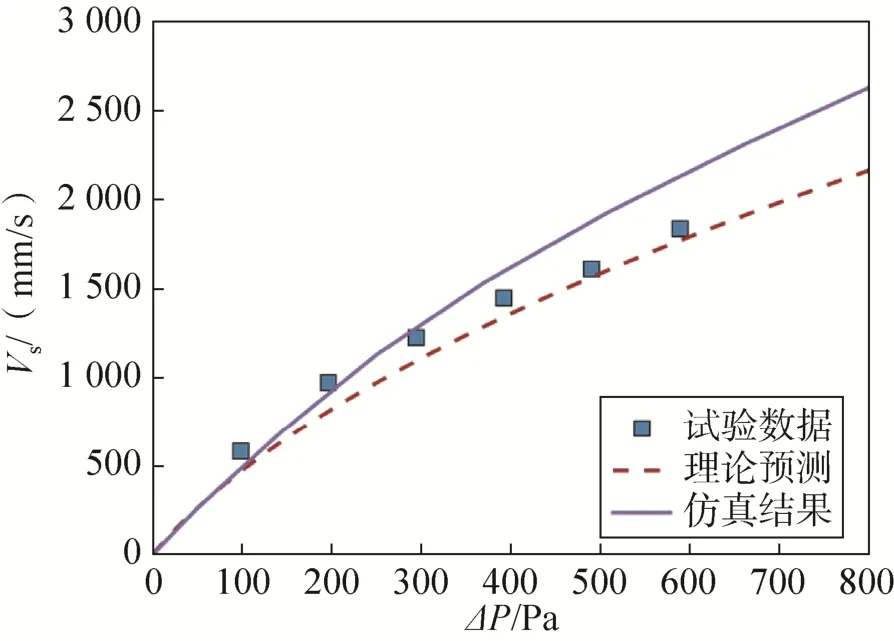
图9 602锦丝绸透气性曲线结果对比Fig.9 Comparison of 602 kam silk porosity curves
图10以602锦丝绸为例给出了织物在不同压差下的外形变化情况,从中不难看出仿真结果在高压差下较预测结果偏大的原因:虽然仿真计算中设置的Ergun系数即为理论预测结果,但是由于在高压差下织物发生较大的弹性变形,织物表面积也随之增大,因此在织物两面压差固定时,透气面积的增大必将引起透气量的增大。对于常规的人员用伞,其工作压差范围为50~300Pa[1],该范围内因织物形变引起的预测偏差较小,本文简化预测模型可以直接应用;而对于在高速来流下工作的稳定伞,可以在式(9)计算的基础上取较为保守的织物相对透气量值进行预测,从而在高压差下获得更可靠的预测结果。
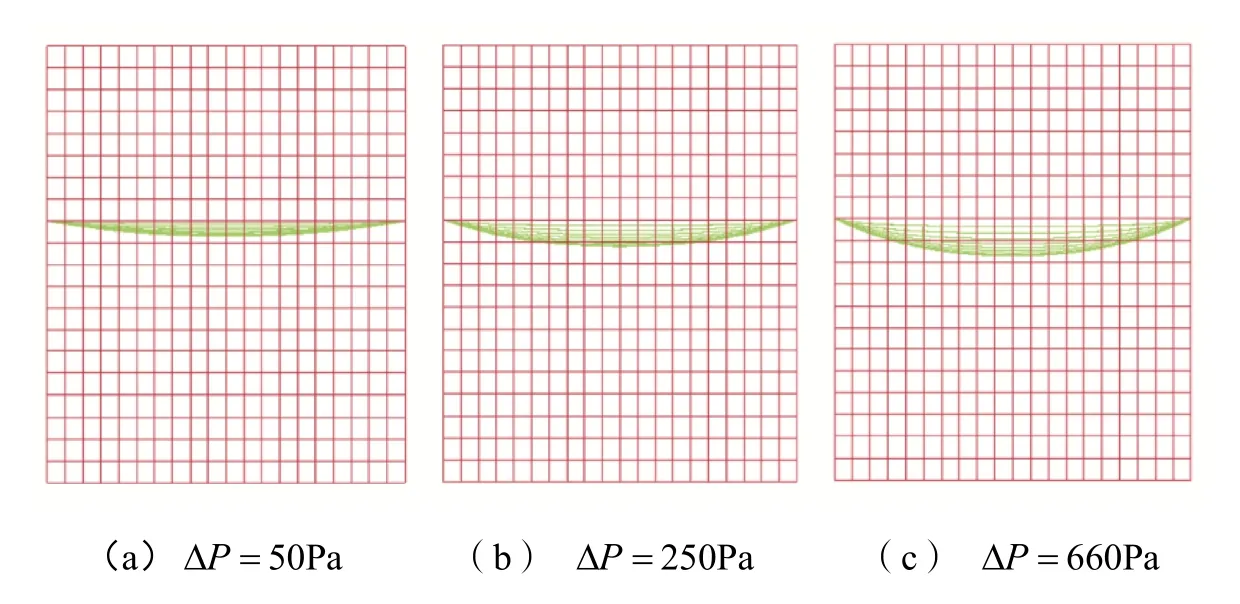
图10 602锦丝绸在不同压差下的外形变化Fig.10 602 kam silk deformation under applied air pressure load
4 结束语
文章根据伞衣织物实际结构特点,以多孔介质透气性理论为基础推导了简化的透气性预测模型,应用该算法对多种常见伞衣织物材料的透气性进行了计算,并将计算结果与各织物材料透气性试验数据以及流固耦合仿真计算数据进行了对比分析,结果表明:
1)简化模型只需标准压差下的透气量数据即可对伞衣织物的透气量方程进行估计,因此可以在缺乏相应透气性试验数据时对各类伞衣织物的压差-透气量曲线进行快速预测;
2)使用简化模型对六种国内外常见伞衣织物透气性进行了理论预测,与试验数据的对比表明简化模型对各类常见伞衣织物具有较好的预测精度;
3)基于ALE方法的织物透气性仿真试验表明:在LS-DYNA流固耦合数值计算中直接应用预测得到的Ergun透气性系数时,高压差下会因织物的弹性变形过大而导致计算得到的透气量结果偏大。
References)
[1]王利荣. 降落伞理论与应用[M]. 北京: 宇航出版社, 1997: 7-10. WANG Lirong. Parachute Theory and Applications[M]. Beijing: China Astronautic Publishing House, 1997: 7-10. (in Chinese)
[2]KNACKE T W. Parachute Recovery Systems Design Manual[R]. Virginia: DTIC Document, 1991: 5-71.
[3]EWING E G, BIXBY H W, KNACKE T W. Recovery Systems Design guide[R]. Virginia: DTIC Document, 1978: 287-291.
[4]马衍富. 降落伞伞衣织物的设计特点[J]. 产业用纺织品, 2000, 18(8): 14-18. MA Yanfu. Parachute Canopy Fabric Design Features[J]. Industrial Textiles, 2000, 18(8): 14-18. (in Chinese)
[5]马衍富. 降落伞织物的透气性[J]. 产业用纺织品, 1987, 5(1): 26-30. MA Yanfu. Permeability of the Parachute Fabric[J]. Industrial Textiles, 1987, 5(1): 26-30. (in Chinese)
[6]HEINRICH H G. The Effective Porosity of Parachute Cloth[R]. Virginia: DTIC Document, 1966: 6-8.
[7]LAVIER H W. Air Permeability Of Parachute Cloths, Part 2[R]. Virginia: DTIC Document, 1953: 1-3.
[8]RONDEAU N C. The Investigation of Parachute Fabric Permeability Under an Unsteady Pressure Differential[D]. Michigan: ProQuest, UMI Dissertations Publishing, 2013.
[9]GIBSON P W, DESABRAIS K, GODFREY T. Dynamic Permeability of Porous Elastic Fabrics[J]. Journal of Engineered Fibers and Fabrics, 2012, 27(4): 29-36.
[10]GOGLIA M J, LAVIER H W S, BROWN C D. Air Permeability of Parachute Cloths[J]. Textile Research Journal, 1955, 25(1): 296-313.
[11]WANG J, AQUELET N, TUTT B, et al. Porous Euler-lagrange Coupling: Application to Parachute Dynamics[C]. 9th International LS-DYNA Users Conference, Michigan, USA, 2006.
[12]贾贺, 荣伟, 陈国良. 基于 LS—DYNA的降落伞伞衣织物透气性参数仿真验证[J]. 航天返回与遥感, 2009, 30(1): 15-20. JIA He, RONG Wei, CHEN Guoliang. The Parachute Canopy Fabric Permeability Simulation with LS-DYNA[J]. Spacecraft Recovery & Remote Sensing, 2009, 30(1): 15-20. (in Chinese)
[13]张建祥, 王桂芝, 崔金德, 等. 纺织品透气性测试[J]. 印染, 2009, 35(23): 38-40. ZHANG Jianxiang, WANG Guilin, CUI Jinde, et al. Textile Permeability Test[J]. Printing, 2009, 35(23): 38-40. (in Chinese)
[14]SKJETNE E, AURIAULT J L. New Insights on Steady, Non-linear Flow in Porous Media[J]. European Journal of Mechanics-B/Fluids, 1999, 18(1): 131-145.
[15]ERGUN S. Fluid Flow through Packed Columns[J]. Chemical Engineering Progress, 1952, 2(48): 89-94.
[16]北京航空材料研究院. 航空材料数据库[DB]. [2013-10]. http://datacenter.biam.ac.cn/Default.asp. Beijing Institute of Aeronautical Materials. Aeronautical Materials Database[DB]. [2013-10]. http://datacenter.biam.ac.cn/ Default.asp. (in Chinese)
[17]TUTT B. The Application of a New Material Porosity Algorithm for Parachute Analysis[C]. 9th International LS-DYNA User's Conference, Michigan, USA, 2006.
[18]XIAO X L. Modeling the Structure-permeability Relationship for Woven Fabrics[D]. University of Nottingham, 2012.
A Fast Permeability Estimation Method for Parachute Fabric
NING Leiming ZHANG Hongying TONG Mingbo
(College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)
A parachute fabric permeability prediction method is proposed based on the Ergun theory. By applying this method, parachute fabric air permeability can be predicted without sufficient test data. A permeability predictions are made on a variety of common parachute fabrics over a range of pressure differentials, and the predicted results are analyzed by comparing with test data. An FSI model for fabric permeability test simulation is built by using Arbitrary Lagrangian-Eulerian method, the numerical simulation is conducted to further verify the reliability and adaptability of the simplified model. The results from this investigation indicate that the simplified model has high prediction accuracy on a variety of parachute fabrics under parachute operational pressure differentials.
canopy fabric; permeability; Arbitrary Lagrangian-Eulerian (ALE) formulation; fluid-structure interaction; parachute
V244.21
: A
: 1009-8518(2016)05-0010-09
10.3969/j.issn.1009-8518.2016.05.002
宁雷鸣,男,1988年生,南京航空航天大学飞行器设计专业在读博士研究生。研究方向为流固耦合动力学。E-mail: lmn_nuaa@163.com。
(编辑:陈艳霞)
2015-06-05
