基于带数据约束实时系统的互模拟检测方法
2016-02-23李国拯
李国拯,高 正
(南京航空航天大学 计算机科学与技术学院,江苏 南京 210016)
基于带数据约束实时系统的互模拟检测方法
李国拯,高 正
(南京航空航天大学 计算机科学与技术学院,江苏 南京 210016)
带数据约束的实时系统是指一种既带有时间约束又带有数据变量约束的计算系统,其广泛存在于航空航天、工业控制、国防等安全攸关系统,并发挥着至关重要的作用。针对这类系统的形式化建模与验证是确保其正确性和可靠性的重要途径。文中首先研究了组合接口自动机、Z语言、时间自动机的形式规范—CT-ZIA,其能同时描述带数据约束的实时系统的时序行为性质和数据结构性质;其次,为了研究该规范上的互模拟形式化验证,给出了CT-ZIA上的互模拟关系定义;然后,为了互模拟算法的可判定性,对CT-ZIA中的时钟进行等价划分,提出了有限论域CT-ZIA的定义;最后,基于有限论域CT-ZIA模型,给出了其上互模拟检测算法,并说明其正确性。
实时系统;接口自动机;Z语言;时间自动机;互模拟检测
0 引 言
带数据约束的实时系统[1]是指一种既带有时间约束,又带有数据变量约束的计算系统。飞行控制、核反应堆控制以及铁路调度控制等计算机控制系统都属于带数据约束的实时系统。这些系统中许多动作的完成都与时间相关,即要满足一定的时间限制,如某个动作要在一秒钟内完成;同时这些系统中数据变量之间也有一定的约束关系,如飞机的飞行速度可能跟气压、温度等有一定的约束关系。单一的规范技术很难适合这样的应用场景,所以这就要求利用多种能够描述系统行为各个方面的专门技术。基于这一想法,在文献[2]中提出了组合接口自动机、时间自动机和Z语言的形式规范。
接口自动机(Interface Automata)[3]是一种轻量级的基于自动机语言的组件规范语言,能够描述基于组件系统中组件及组件间的交互行为。时间自动机(Timed Automata)[4]是使用最为广泛的一种描述实时系统的数学模型,可简单看作带时钟变量的有限自动机。Z[5]是基于一阶谓词逻辑和集合论的形式规格语言。
文中研究了一种组合接口自动机、时间自动机和Z语言的规范语言,即CT-ZIA[2]。接口自动机是描述软件组件接口性质的直观模型,时间自动机是描述实时系统的模型,Z可以描述状态的数据性质以及状态的变迁。为了对复杂实时系统进行规范说明,这里简单介绍下CT-ZIA的定义,粗略地讲,CT-ZIA具有时间自动机风格和特点,但它的状态和操作是用Z语言来描述的。文中进一步研究了CT-ZIA上的互模拟关系,并给出了有限论域CT-ZIA上的互模拟检测算法。
1 连续时间ZIA规范
在文献[2]中,提出了CT-ZIA规范,并研究其上的模型检测[6]问题,下面直接给出其定义:
(1)SP是状态的集合;
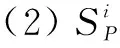
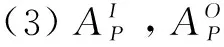
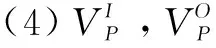
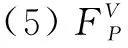
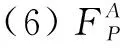
(7)X为时钟变量的非负实数有限集合,C(X)为X上时钟约束的集合,其语法定义如下:
Φ::=xc|cx|ø1∧ø2
其中,x∈X;∈{<,≤};c为非负有理数。
(8)映射I:SP→C(X)为每个状态赋以一时间约束,此约束称为节点不变量;
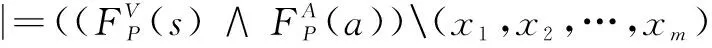
2 CT-ZIAs间的互模拟关系
互模拟[7-8]是进程演算里的一个十分重要的概念,用来研究并发系统行为的一种方法。在软件系统里,互模拟通常用来描述抽象规格说明与可执行程序代码的相互转换过程,所以互模拟关系的目的在于形式化说明相同组件的抽象和具体版本之间的关系,例如接口的规范与其实现之间的关系。
对于某个Z模式A,使用VI(A)代表A中的输入变量集合,VO(A)代表A中的输出变量集合,VH(A)表示A中的内部变量集合。
为了定义Z模式之间的互模拟关系,需要如下的符号。
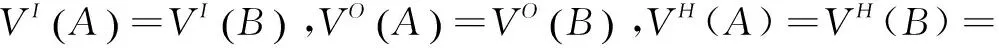
直观上,A≃B意味着模式A和模式B有相同的输入变量和相同的输出变量,并且模式A和模式B的输入变量范围和输出变量范围一样。
现在给出Z模式之间的互模拟关系,其描述了状态的数据结构属性间的互模拟关系。粗略地讲,对于模式A和模式B,说A和B是互模拟的,就是两者的输入输出变量一样,并且两者的输入变量范围和输出变量范围也一样。
定义3:考虑两个Z模式A和B,使用符号A≅B,如果
(1)VI(A)=VI(B),VO(A)=VO(B);
(2)A(x1,x2,…,xm)≃B(y1,y2,…,yn),其中{x1,x2,…,xm}=V(A)-VI(A)-VO(A),{y1,y2,…,yn}=V(B)-VI(A)-VO(A)。
接下来给出CT-ZIAs间的互模拟关系。对CT-ZIAs来说,状态不仅有数据属性,还有行为属性。因此,CT-ZIAs间的互模拟关系既包含数据属性间的互模拟关系,又包含行为属性间的互模拟关系。
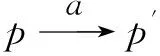
定义4:给定一个CT-ZIAP,定义有序对(s,DP)∈SP×为P在某个时刻的状态,其中是实数集合。下面定义P中的状态变迁:
定义5:考虑CT-ZIAP和CT-ZIAQ,称二元对称关系R⊆(SP×)×(SQ×)是互模拟关系,需对(s,DP)∈SP×,(t,DQ)∈SQ×,(s,DP)R(t,DQ)推出如下条件满足:
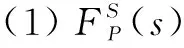
(2)对于时延d∈+,如果,那么存在时延d′∈+,使得以及;并且如果,那么存在时延d′∈+,使得以及;

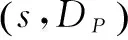
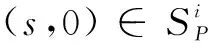
3 有限论域CT-ZIA
考虑一个CT-ZIAP以及其上的状态有序对(s,DP)∈SP×,显然,P是一个无限状态系统,为了互模拟算法的可判定性,需要首先将无限状态转为有限状态。为了获得CT-ZIA无限状态空间的有限描述,下面给出有限论域CT-ZIA的定义。
Alur,Courcoubetis和Dill在文献[9-10]中提出一种时钟等价方法,把时间自动机等价为域自动机,但是按照Alur时钟等价方法构造出的域自动机,存在状态空间迅速膨胀爆炸的问题。在文献[2]中,笔者采用一种优化的时钟等价方法,并在此基础上定义了适合于优化时钟等价规则的域自动机,使等价后的域自动机状态数尽量少[11],这样就将CT-ZIA等价为一种带Z的域自动机。
大体思想如下:在构建时钟等价规则时,主要考虑时钟关键点的相互比较。例如,对状态s来说,约束条件x≥2中的约束常量2是一个关键点,对于x的赋值v(x)来说,当v(x)>2或v(x)<2时,无论取何值都是不相关的,所以仅需要考虑约束常量这个关键点就可以了。
综上所述,对时钟x而言,可分为三种情况:
(1)v(x) (2)v(x)=cx则v'(x)=cx; (3)v(x)>cx则v'(x)>cx。 类似的,对于y-x的取值范围,只需要考虑时钟关键点的比较。 如上方法将CT-ZIA等价为一种带Z的域自动机,下面对CT-ZIA中Z模式再加以适当的约束,就得到一类特殊的CT-ZIAs,其上的互模拟检测算法是可判定的。 定义7:给定一个Z模式S[v1:T1;…;vm:Tm|P1;…;Pn],如果模式中的每个变量vi有有限多可能的值,即变量的类型Ti有有限多元素,那么称S为有限域Z模式。考虑一个,称其为有限论域CT-ZIA,需满足如下条件: 给定一个CT-ZIAP,可以将P转为等价的带Z域自动机,进一步约束P中Z模式的变量取值,就得到有限论域CT-ZIA,记为F(P)。这部分给出针对有限论域CT-ZIAs的互模拟检测算法BC。假定F(P)和F(Q)是两个有限论域CT-ZIAs,具体算法如下: BC(P,Q)= Rp,q:=BCS(p,q) BCS(p,q)= return(Bp,q) elseB:=∧a∈A(p,q)Matcha(p,q) Matcha∈A(p,q)(p,q)= return(false) return(false) Di,j:=BCS(pi,qj) return(∧i(∨j(Ca∧Ci,j∧Di,j))) BCZ(S,T)= if(VI(S)≠VI(T))or(VO(S)≠VO(T)) thenreturn(false) else VT:=V(T)-VI(S)-VO(S) E:=BCL(SVS,TVT) return(E) BCL(M,N)= TV(LS)= rewriteschemaLStoanequivalentfirstorderlogicalformulaLF if(LFisalwaystrueforanyassignmentonvariables)thenreturn(true) elsereturn(false) 在上面的算法中,如果对任意赋值LS总是返回true,那么函数TV(LS)返回true。一般,因为一阶逻辑的重言式问题是不可判定的,所以函数TV(LS)不能被实现,但是如果只考虑某些可判定的子逻辑,比如,逻辑公式的每个变量有有限多可能的值,这样的子逻辑的重言式问题就是可判定的。因为LS是有限域Z模式,每个变量仅有有限多的可能的取值。 不难证明上文提出的互模拟检测算法的正确性。下面给出上面算法的正确性说明: 引理1:算法BCZ(S,T)可以终止,并且是正确的,即算法返回true当且仅当S≅T。 证明:由Z模式的精化关系定义可得引理1是正确的。 引理2:算法BCS(p,q)可以终止,并且是正确的,即算法返回true,当且仅当p~q。 证明:函数BCS(p,q)从有限划分后的系统初始状态有序对(p,q)出发,通过匹配从它们出发的变迁来检测p,q之间的相似性。在遍历变迁图的过程中,算法根据CT-ZIA的变迁从每个状态有序对产生接下来的变迁以及状态,然后通过模拟来匹配变迁,如果匹配成功,算法就进入了下一对状态有序对。函数Matcha在两个变迁图的乘积图上执行深度优先的算法,如果一个状态不能匹配另外一个状态的变迁,那么它们间就不是互模拟关系,函数返回false,否则返回true。将P和Q进行了有限划分得到有限状态系统F(P)和F(Q),这就保证了仅会有限次调用函数Matcha(p,q),所以,函数BCS(P,Q)总是会终止。 通过上面的引理,即可得出下面的命题: 命题1:算法BCS(P,Q)可以终止,并且是正确的,即算法返回true当且仅当P~Q。 为了研究带有数据约束的实时系统,文献[2]中提出了组合接口自动机、时间自动机和Z语言三种形式规范说明技术的模型(CT-ZIA),研究了其上的模型检测问题,但是未对该模型进行进一步研究;文献[12]提出了一种基于离散时间的ZIA规范,但是基于离散时间的模型较适用于同步系统;文献[13]提出了混成ZIA模型,并给出了其上的近似精化关系定义,由于混成ZIA多数子集的不可判定性,未给出精化检测算法。 文中给出了CT-ZIAs间互模拟关系的定义,并对CT-ZIAs中的时钟进行等价划分,给出有限论域CT-ZIA的定义,在其上的互模拟检测算法是可以判定的,这对自动化验证组件的规范与实现的关系有重大意义。 [1] 李广元,唐稚松.带有时钟变量的线性时序逻辑与实时系统验证[J].软件学报,2002,13(1):33-41. [2] 倪水妹,曹子宁,李心磊.带数据约束实时系统的模型检测[J].计算机科学,2014,41(5):254-262. [3]deAlfaroL,HenzingerTA.Interfaceautomata[C]//ProcofACMSIGSOFTsoftwareengineeringnotes.[s.l.]:ACM,2001:109-120. [4] Alur R,Dill D L.A theory of timed automata[J].Theoretical Computer Science,1994,126(2):183-235. [5] Spivey J M.The Z notation:a reference manual[M].UK:Prentice Hall International Ltd,1992. [6] 戎 玫,张广泉.模型检测新技术研究[J].计算机科学,2003,30(5):102-104. [7] 朱维军,刘保罗,周清雷.时间自动机与信号自动机的互模拟算法[J].华南理工大学学报:自然科学版,2008,36(5):38-42. [8] 李 娜,姚从军.互模拟的一些基本性质[J].云南师范大学学报:哲学社会科学版,2010,42(5):68-73. [9] Alur R.Techniques for automatic verification of real-time systems[D].Stanford:Stanford University,1991. [10] Alur R,Courcoubetis C,Dill D.Model-checking for real-time systems[C]//Proceedings of fifth annual IEEE symposium on logic in computer science.[s.l.]:IEEE,1990:414-425. [11] 钱俊彦,赵岭忠,古天龙.一种基于时间自动机的时钟等价性优化方法[J].计算机工程,2005,31(18):71-73. [12] 狄杨思.形式规范的自动验证算法的研究[D].南京:南京航空航天大学,2012. [13] Cao Z,Wang H.Hybrid ZIA and its approximated refinement relation[C]//Proceedings of the 6th international conference on evaluation of novel approaches to software engineering.Beijing,China:[s.n.],2011:260-265. An Approach of Bisimulation Checking for Real-time System Based on Data Constraints LI Guo-zheng,GAO Zheng (School of Computer Science and Technology,Nanjing University of Aeronautics & Astronautics,Nanjing 210016,China) Real-time systems with data constraints refer to computing systems both with time-bound and data variables constraints,which is widely used in safety-critical areas like aerospace,industry control,defense system,playing an important role.Formal modeling and verification for these systems is an important way to ensure the correctness and reliability of the systems.In this paper,study a specification model combining interface automata,timed automata and Z language,named CT-ZIA.This model can be used to describe temporal properties and data properties of real-time systems with data constraints.Second,in order to study formal verification for bisimulation in the specification,the bisimulation definition for CT-ZIA is given.Then,for the decidability of simulation algorithm,each clock of CT-ZIA is partitioning in equivalence,putting forward the definition of limited domain CT-ZIA’s.Finally,give an algorithm for checking bisimulation relation between CT-ZIAs with finite domain and demonstrate the correctness of the algorithm. real-time system;interface automata;Z notation;timed automata;bisimulation checking 2014-11-25 2015-03-04 时间:2016-01-04 航空科学基金(20128052064);中央高校基本科研业务费专项资金(NZ2013306);国家“973”重点基础研究发展计划项目(2014CB744903) 李国拯(1990-),男,硕士研究生,研究方向为形式化方法、模型检测。 http://www.cnki.net/kcms/detail/61.1450.TP.20160104.1608.084.html TP311 A 1673-629X(2016)01-0006-04 10.3969/j.issn.1673-629X.2016.01.0024 互模拟检测算法
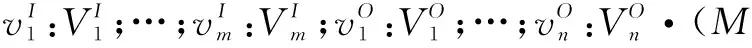
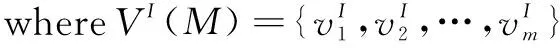
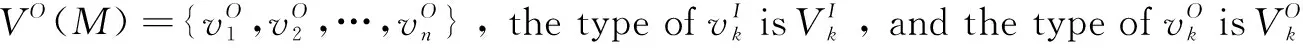
5 结束语
