一种新的相干信源互耦自校正算法

李磊， 李国林

(1.解放军第91872部队，北京 102400；2.海军航空工程学院七系，山东，烟台 264001)

一种新的相干信源互耦自校正算法

李磊1， 李国林2

(1.解放军第91872部队，北京 102400；2.海军航空工程学院七系，山东，烟台 264001)

针对互耦效应下相干信源的波达方向(direction of arrival， DOA)估计问题，提出一种基于阵列接收数据一阶统计量的解相干及互耦自校正算法. 算法利用阵元接收数据的一阶统计量构造伪协方差矩阵，理论推导证明，互耦系数已从理想导向矢量中剥离，且该矩阵的秩与信源相关性无关，仅与信源个数相等，即实现了信源的解相干及互耦自校正，因此通过对重构矩阵进行一次特征分解即可实现DOA估计. 此外，对算法的子空间估计性能及由互耦系数导致的测角模糊性进行了分析，结果表明该算法实现过程简单，计算量小，在低信噪比和短快拍数时仍具有很高的估计性能. 仿真结果验证了算法的有效性.

相干信源；互耦；一阶统计量；DOA估计

波达方向估计是阵列信号处理领域的一个重要研究方向，在雷达、通信、无线电探测等领域具有广泛的应用[1-4]. 大多数超分辨空间谱估计算法均以阵列流型精确已知、阵元之间相对独立为前提，但在实际中，受多种误差(如阵元幅相误差、阵元位置误差、互耦等)影响，理想阵列流型会出现偏差或扰动，导致估计性能急剧恶化.

目前，阵列互耦误差校正的主流方法是参数化估计方法，包括有源校正类、辅助阵元类和自校正类算法. 其中，自校正算法不需要方位已知的辅助信源及精确校正的辅助阵元，可以实时在线完成误差参数的估计与校正，因而得到广泛应用[5]. 文献[6-8]提出了一种能够实现在线方位估计的迭代优化类算法，校正精度较高，但无法保证全局收敛性，且需要循环优化及多维搜索过程，导致算法的实时性差. 王伟等[9]为避免文献[6-8]中全局收敛性及多维搜索问题，将双基地MIMO雷达的互耦参数估计转化为线性约束二次最小化问题，但该算法不适用于多径相干信源背景. 王布宏等[10]及Sellone等[11]利用ULA(uniform linear array， ULA)阵列互耦矩阵的带状对称Toeplitz特性，构造导向矢量的转换函数，提出一类秩损估计(rank reduction estimation， RARE)算法，实现了互耦与DOA的联合估计，Hu等[12]将该思想推广至二维阵列中，但转换函数不具备通用性，需要根据互耦自由度而定，且上述算法仅适用于非相干信源背景下的DOA估计及互耦误差自校正.

基于阵列接收数据的一阶统计量，本文提出一种相干信源DOA估计及互耦自校正方法，实现过程简单、计算量小，且在低信噪比和短快拍时仍能保持很高的估计性能，为互耦条件下的相干信源DOA估计提供了一个新的思路.

1 阵列及互耦模型

假设空间有2M+1个各向同性阵元组成均匀线阵，阵元编号为-M，…，0，…，M，阵元间距为d，如图1所示.N个中心波长为λ且均值非0的远场窄带信号sk(t)，k=1，2，…，N分别以与线阵法线夹角为θk的方向入射至阵列. 阵列噪声为0均值高斯白噪声，阵元间噪声彼此独立，且噪声与信号相互独立.

以线阵的中间阵元(编号为0)为参考原点，则第i个阵元的接收数据为

(1)

(2)

式中ni(t)为第i个阵元的加性高斯白噪声.

阵列接收数据的矩阵矢量形式可表示为

(3)

当考虑阵元间互耦效应时，阵列接收数据的矩阵矢量形式为

(4)

式中C为由矢量c形成带状对称Toeplitz互耦矩阵. 当阵元间的互耦自由度为p时，C可表示为

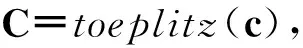
(5)式中c为2M+1维矢量，且有

c=[c0c1… cp0 … 0]，

2 基于一阶统计量的相干信源DOA估计及互耦自校正方法

本节利用ULA阵列互耦矩阵的带状对称Toeplitz特性进行有效子阵的选取，并通过其阵元接收数据的一阶统计特性构造伪协方差矩阵实现解相干及互耦自校正.

2.1 有效子阵选取

设互耦自由度为p，选取阵列中间2M-2p+3个阵元组成新的子阵，即阵列中编号为-(M-p+1)，…，M-p+1的阵元，则新阵列接收的快拍数据可表示为

(6)

式中：

(7)

(8)

定义c(θ)如下

(9)

将式(2)代入至式(9)中，则易推得

(10)

则式(6)可重新表示为

(11)

第i个阵元的接收数据可重新表示为

(12)

由式(12)可知，若c(θ)=0，则阵列在该方向上接收数据为0. 实际上，c(θ)等效于一个波束形成器的加权系数，当c(θ)=0时，波束形成器在该方向上形成0点，此时该方向为DOA估计的盲点，下文将对由互耦系数引起的测角模糊及应对措施进行分析.

2.2 基于一阶统计量的伪协方差矩阵构造

结合式(12)中阵元接收数据表达式，阵列接收数据的一阶统计量定义为

(13)

式中mk=E[sk(t)]≠0，k=1，2，…，N为入射信源的均值.

需要说明的是，本文算法要求入射信源均值非0，若信源均值为0，则下文构造的伪协方差矩阵会发生秩亏，则无法达到解相干的目的，这对算法的应用范围具有一定的局限性. 同时，由于阵元噪声均值为0，则mxi不含噪声分量，因此算法无需额外的去噪处理.

下面利用阵列接收数据的一阶统计量mxi构造M-p+2维伪协方差矩阵Rxx为

(14)

由式(13)及导向矢量特点可得

(15)

则易推得

(16)

(17)

与常规子空间类算法不同，本文构造的等效信号协方差矩阵Rss对角元素不再表示信号功率，而表示信源均值与互耦系数的乘积. 由式(16)及式(17)可知，矩阵Rss为对角阵，则矩阵的秩与信源个数相同，而与信源之间的相关性无关，即实现了解相干；同时，互耦系数c(θk)已从理想阵列流型矩阵剥离至等效信号协方差矩阵Rss中，即对该矩阵进行特征分解后得到的信号子空间US和噪声子空间UN不受互耦及信号相关性的影响. 结合MUSIC算法，利用谱峰搜索即可实现对入射信源的DOA估计. 谱估计器表达式为

(18)

3 算法仿真分析

本文所提算法为一种子空间类DOA估计算法，仿真中为方便对比，将文献[4]中未考虑互耦效应的修正空间平滑MUSIC算法(SS-MUSIC)作为对比算法. 假设3个远场窄带相干信号分别从-20°、30°和40°方向入射至图1阵列，设定阵元参数M=10，阵元间距d=λ/2，角度搜索区间为[-90°，90°]，搜索步长为1°.

3.1 子空间估计性能分析

子空间估计性能是决定子空间类算法DOA估计性能的关键因素. 两个子空间的距离定义为

(19)

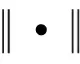
(20)

设定信噪比RSNR=10 dB，快拍数从50～1 800区间以50次为步长递增，每个快拍数下进行1 000次独立Monte-Carlo统计仿真，计算其均值作为子空间平均距离. 仿真结果如图2所示.

可以看出，通过本文算法估计的信号子空间和文献[4]中基于常规特征分解所得信号子空间是非常相近的.

它们与真实信号子空间距离之差在快拍数等于50次时仅为0.03，当快拍数变得更大时，其距离之差逐渐减小至0.003，从而证明了本文方法估计到的信号子空间和基于常规特征分解得到的信号子空间是等价的.

3.2 算法DOA估计有效性分析

不改变阵列模型及信号入射方向，考虑阵元间的互耦效应，为验证互耦效应对算法相干信源估计性能的影响，做如下仿真. 仿真时设定信噪比RSNR=10 dB，快拍数为200次，互耦自由度p=3，互耦系数矢量

c=[1 0.788 1+0.520 5i 0.326 6+0.255 1i 0 … 0]T.

本文算法在有互耦、无互耦及文献[4]中SS-MUSIC算法在有互耦时的仿真结果如图3所示.

由图3可以看出，本文算法能够实现互耦条件下的相干信源DOA估计，且在有互耦时的估计效果与无互耦时估计效果相差不大，而文献算法在互耦条件下的估计性能下降严重甚至估计错误. 分析其原因，一方面，本文算法利用一阶统计量构造等效信号协方差矩阵的秩仅与信源个数相同，而与信源之间的相关性无关，实现了信源解相干；另一方面，本文算法将互耦系数从理想阵列流型矩阵剥离，确保了算法估计的信号子空间和噪声子空间不受互耦及信号相关性的影响.

3.3 算法测角模糊性分析

仅改变互耦系数，为验证互耦系数导致的测角模糊进行如下仿真. 仿真时设定信噪比RSNR=10 dB，快拍数为200次，互耦系数矢量改变为c=[1 0.887 1+0.452 5i 0.5 0 … 0]T，互耦自由度p=3，本文算法在有互耦和无互耦时的仿真结果如图4所示.

显然，本文算法仍能正确估计出-20°和40°方向的入射信源，但在30°方向漏峰，且在别的方向出现伪峰. 分析其原因，当θ=30°时，导致c(θ)=0，阵列在该方向上接收数据为0，无法完成该方向DOA估计. 通过阵列设计时进行参数调整，即可在角度搜索范围内满足c(θ)≠0，实现对所有入射角度的DOA估计.

3.4 算法统计性能分析

不改变阵列模型及信号入射方向，分别改变信噪比与快拍数，验证本文算法的均方根误差(root-mean-square error， RMSE)随信噪比和快拍数的变化关系，仿真时以文献[4]中SS-MUSIC算法作为对比算法. DOA估计的RMSE定义为

(21)

图5(a)为本文算法及SS-MUSIC算法分别在有互耦和无互耦时的RMSE随SNR变化关系，仿真设定快拍数为200次，信噪比从0～20 dB区间以1 dB的步长递增，每个信噪比下分别进行100次独立Monte-Carlo统计仿真，估计偏差为所有仿真的均值. 可以看出，随着信噪比的增大，本文算法及无互耦的SS-MUSIC算法的RMSE都逐渐减小，而有互耦时的SS-MUSIC算法在信噪比3 dB之后基本保持在1.7°的误差. 其中，本文算法在有互耦时的估计误差始终高于无互耦时本文算法，而无互耦时的SS-MUSIC算法的估计误差始终保持最低，这是以大量互相关运算及平滑处理所带来的计算量为代价. 在RSNR=0 dB时，本文算法有互耦时的RMSE仅约为0.55°，即在低信噪比下保持了较高的估计性能.

图5(b)为本文算法及SS-MUSIC算法分别在有互耦和无互耦时的RMSE随快拍数变化关系，仿真设定信噪比RSNR=10 dB，快拍数从50～1800区间以50的步长递增，每个快拍数分别进行100次独立Monte-Carlo统计仿真，估计偏差为所有仿真的均值. 显然，所有算法的RMSE随快拍数的变化趋势与RMSE随SNR的变化趋势基本一致. 在快拍数为50次时，本文算法有互耦时的RMSE仅约为0.45°，即在短快拍数时同样保持了较高的估计性能. 同时，该仿真从统计性能定量分析的角度证明了本文算法较高的子空间估计性能.

4 结束语

在实际测向系统中，阵元间存在互耦效应，且多径效应会导致被测空间存在相干信源，严重影响DOA估计性能. 笔者以实际工程应用为背景，提出一种基于一阶统计量的相干信源DOA估计及互耦自校正方法. 算法利用阵列接收数据的一阶统计量构造伪协方差矩阵，由公式推导可知，互耦系数已从理想导向矢量中剥离，且矩阵的秩仅与信源个数相等，即实现了信源的解相干及互耦自校正. 算法利用阵列接收数据的一阶统计量代替传统算法中的二阶或高阶统计量，实现过程简单，计算复杂度低且在低信噪比和短快拍时仍能保持很高的估计性能. 如何将本文思想推广至二维DOA估计及互耦自校正是下一步的工作重点.

[1] Chen Chen， Zhang Xiaofei， Chen Han， et al. A low-complexity algorithm for coherent DOA estimation in monostatic MIMO radar[J]. Wireless Pers Commun， 2013，72(1):549-563.

[2] Zheng Zhi，Li Guangjun， Teng Yunlong. Simplifi estimation of 2D DOA for coherently distributed sources[J]. Wireless Pers Commun， 2012，62(4):907-922.

[3] Dandekar K R， Ling H， Xu G. Effect of mutual coupling on direction finding in smart antenna applications[J]. Electronics Letter， 2000，36(22):1889-1891.

[4] 董玫，张守宏，吴向东，等.一种改进的空间平滑算法[J].电子与信息学报，2008，30(4):859-862.

Dong Mei， Zhang Shouhong， Wu Xiangdong， et al. An improved spatial smoothing technique[J]. Journal of Electronics & Information Technology， 2008，30(4):859-862.(in Chinese)

[5] 王永良，陈辉，彭应宁，等.空间谱估计理论与算法[M].北京:清华大学出版社，2004:117-122.

Wang Yongliang， Chen Hui， Peng Yingning， et al. Spatial spectrum estimation theory and algorithms[M]. Beijing: Tsinghua University Press， 2004:117-122. (in Chinese)

[6] Friedlander B， Weiss A J. Direction finding in the presence of mutual coupling[J]. IEEE Trans on Antennas and Propagation， 1991，39(3):273-284.

[7] Khallaayoun A， Weber R J， Yikun H. A blind terative calibration method for high resolution DOA estimation[C]∥Proceedings of the Mititary Communication Conference. [S.l.]: IEEE， 2011:199-204.

[8] Sellone F， Serra A. A novel online mutual coupling compensation algorithm for uniform and linear arrays[J]. IEEE Trans on Signal Processing， 2007，55(2):560-573.

[9] 王伟，王咸鹏，李欣.双基地MIMO雷达多目标定位及互耦参数估计[J].华中科技大学学报，2012，40(7):78-83.

Wang Wei， Wang Xianpeng， Li Xin. Multi-target localization and estimation of mutual coupling bistatic MIMO radars[J]. J Huazhong Univ of Sci& Tech， 2012，40(7):78-83. (in Chinese)

[10] 王布宏，王永良，陈辉.均匀线阵互耦条件下的鲁棒DOA 估计及互耦自校正[J].中国科学E辑:信息科学，2004，34(2):229-235.

Wang Buhong， Wang Yongliang， Chen Hui. Robust DOA estimation and mutual coupling self-calibration algorithm for uniform linear array[J]. Science in China Series E: Technological Sciences， 2004，34(2):229-235. (in Chinese)

[11] Sellone F， Serra A. A novel mutual coupling compensation algorithm for uniform and linear arrays[J]. IEEE Trans on Signal Processing， 2007，55(2):560-573.

[12] Hu X Q， Chen H， Wang Y L， et al. A self-calibration algorithm for cross array in the presence of mutual coupling[J]. Science China， Information Sciences， 2011，54(4):836-848.

(责任编辑：李兵)

A Novel Self-Calibration Algorithm for Coherent Signal Sources

LI Lei1， LI Guo-lin2

(1.Unit 91872 of PLA， Beijing 102400， China; 2.Department 7 of Naval Aeronautical Engineering Institute， Yantai，Shandong 264001， China)

To estimate direction of arrival (DOA) for coherent signal sources in the presence of mutual coupling， a novel self-calibration and decorrelation method was presented based on the first order statistics of array received data. A pseudo covariance matrix was constructed by the first order statistics. Theoretical analysis proves that， the rank of the matrix was determined by the number of signals， without any relation with the coherency of signals. The mutual coupling coefficients have already been isolated from the ideal steering vectors. This shows that DOA estimation can be achieved by performing once decomposition to the reconstructed matrix. Moreover， the performance of subspace estimation and the fuzziness of DOA estimation caused by mutual coupling coefficients were analyzed respectively. Results show that， the proposed method has high performance under scenarios of low SNR and snapshot deficiency with simple implementation and low computational complexity. Simulations present the effectiveness of the method.

coherent signal sources; mutual coupling; first order statistics; DOA estimation

2014-05-14

李磊(1987—)，男，博士生，E-mail：lilei19880229@163.com；李国林(1954—)，男，教授，博士生导师，E-mail:liguolin@163.com.

TN 911.7

A

1001-0645(2016)12-1303-06

10.15918/j.tbit1001-0645.2016.12.018