基于鲁棒微分器的全阶非奇异终端滑模再入姿态控制

赖汝， 金震， 盛永智， 刘向东

(北京理工大学 自动化学院，北京 100081)

基于鲁棒微分器的全阶非奇异终端滑模再入姿态控制

赖汝， 金震， 盛永智， 刘向东

(北京理工大学 自动化学院，北京 100081)

针对飞行器再入段的强耦合和非线性的问题，提出了一种基于鲁棒微分器(robust exact differentiator， RED)的全阶非奇异终端滑模控制(full-order nonsingular terminal sliding mode control， FONTSMC)方法. 首先，设计了一种新的全阶非奇异终端滑模函数，保证在控制器中不存在带有分数次幂项的状态量的导数，同时证明了跟踪误差可以在有限时间内收敛到0；然后，针对该滑模运动方程存在误差二阶导数的特殊情况，引入了超螺旋算法(super-twisting algorithm， STA)作为鲁棒微分器(RED)，避免了由直接采用普通微分器引入的干扰噪声. 进一步为了避免滑模控制的抖振问题，采用边界层技术与低通滤波技术共同消除控制量的抖振. 最后，仿真结果验证了所设计的控制器可以实现有限时间姿态跟踪控制，且具有较好的鲁棒性.

全阶终端滑模；非奇异；抖振抑制；鲁棒微分器；姿态控制

飞行器的再入过程会呈现出较为严重的非线性特性. 这些因素导致了对飞行器的姿态进行控制变得异常复杂.

滑模控制方法为实现模型不确定系统的镇定问题提供了一套系统的解决方案[1]，这使得该方法被广泛应用于飞行器姿态控制中. Wang等[2]针对飞行器的姿态控制问题，利用反馈线性化进行解耦，对三通道分别设计了指数时变滑模控制器. Geng等[3]针对可重复使用的飞行器控制问题设计了有限时间终端滑模控制器. Sun等[4]设计了一个全新的有限时间滑模函数，实现了对高超声速飞行器巡航段的有限时间控制. Yu等[5]提出了终端滑模控制(terminal sliding mode control， TSMC)的概念. 与传统滑模控制器相比，终端滑模有限时间收敛的性质为控制器提供了更多的优势. 比如，更快的收敛速度、更高的控制精度以及更强的鲁棒性[6]. 然而，终端滑模控制方法仍然存在着两个主要问题：控制输出奇异与抖振问题.

针对控制量输出奇异问题，众多的专家学者都提出了相应的解决方法. 这些方法具体可以分为两类：一类是间接方法，如文献[7-8]中提出的终端滑模与传统滑模之间切换控制或将系统跟踪轨迹转化到一个事先定义的开区域等方法，然而该方法会增加原终端滑模的收敛时间；另一类是文献[9]中提出的非奇异终端滑模控制方法，属于直接方法.

为了避免上面方法的缺陷，本文引入了全阶滑模的概念. 在传统的滑模控制中，滑模函数的阶次低于系统状态空间的阶次，通常称此类滑模运动是降阶的. 近年来，Ackermann[10]、Ha等[11]提出了全阶滑模控制器的概念，即滑模面的阶次与系统状态方程的阶次相同. 将该思想用于终端滑模控制器设计中，可以有效避免控制输出的奇异问题. 然而，当采用全阶滑模思想设计终端滑模时，需要在滑模面中引入状态的二阶导数信息，该信息在实际中是不可测得的. 针对该问题，Levant[12]提出了超螺旋算法 (STA)，该算法可以用作控制器、状态估计器和鲁棒微分器(RED)，文献[12-13]中对其进行了详细分析. 当超螺旋算法作为鲁棒微分器对系统中某些状态的导数信息进行估计时，可以避免传统微分器存在的放大测量信号中的干扰噪声的问题. 同时可以保证估计误差在有限时间内收敛到0.

针对滑模控制输出抖振问题，相关学者从不同角度提出了解决方法，其中有边界层技术[14]、高阶滑模法[15]和滤波器法[16]等. 目前常用的方法是引入边界层，采用饱和函数或相应连续函数近似代替非连续的符号函数，该方法对于消除抖振方面具有一定的作用. 高阶滑模方法是将不连续的切换函数项转移到控制器的高阶导数中去，得到连续的动态滑模控制律，有效地降低了抖振. 滤波器方法是通过对控制器输出进行平滑滤波以达到消除抖振的目的.

1 再入飞行器数学模型及简化处理

本文采用文献[17]中提供的再入飞行器的模型，为简化在线计算以及控制器的设计，在建立数学模型时考虑如下假设：① 在建模时忽略地球的角速度；② 忽略了飞行器位移运动的影响；③ 由于再入过程中采用BTT控制策略，因此满足条件：β≈0.

将文献[17]中的非线性方程组写成多输入多输出的非线性仿射系统的形式，如下所示

(1)

式中：

对系统(1)进行反馈线性化处理，可得

式中：F(x)，E(x)由反馈线性化得到，且

det(E(x))=-1/I*Izz≠0，

因此控制器可以设计为

(2)

由此可得

(3)

式中：v=[v1v2v3]为引入的辅助变量，Δv为系统中的聚合扰动.

2 姿态控制器设计

本节给出基于鲁棒微分器(RED)的全阶非奇异终端滑模(FONTSMC)姿态控制器设计方法. 首先考虑如下引理：

引理1[18]对于系统(3)，当采用如下式的状态反馈控制律(FDC)，则可以保证系统(3)的状态量在有限时间内收敛到0.

(4)

2.1 滑模面设计

为了避免传统终端滑模中的奇异问题，设计如下的全阶终端滑模面

(5)

式中：S(t)=[s1(t)s2(t)s3(t)]T，一旦系统状态到达理想滑模面S(t)=0，则系统(3)将会变为有限时间稳定的双积分系统，由引理1可知，系统误差将在有限时间内收敛到0.

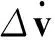
(6)

式中：ldmin，kdmin为矩阵ld，kd中非0元素的最小值，且有矩阵

ld=diag[ld1ld2ld3]，

kd=diag[kd1kd2kd3].

(7)

式中：θ的取值范围与式(3)相同；η=diag[η1η2η3]为切换增益矩阵.

证明 选择如下Lyapunov函数

对上式求导可得

(8)

将式(7)中的v带入式(5)的S(t)中，可得

(9)

对式(9)求导可得

将此式带入式(8)，可得如下关系式

解上面的微分方程可知，Vs收敛到0所用的时间为

(10)

因此，S(t)将会在有限时间内收敛到0. 证毕.

本文为了减弱滑模控制器固有的抖振问题，在切换控制中引入了一阶低通滤波器以达到消抖的作用(为了推导方便采用积分环节代替，效果相同). 进一步，为了使控制器的输出更加平滑，采用饱和函数代替切换控制中的符号函数，则等效控制项可重新表示为如下形式

式中φj为边界层厚度.

2.2 鲁棒微分器(RED)

在本节中将引入鲁棒微分器，对滑模函数中的姿态角二阶导数信息进行估计.

Levant在文献[19]中提出了鲁棒微分器的构造原理，下面将其引入到本文中.

(11)

为了使观测误差在有限时间内趋近于0，设计的鲁棒微分器如下

式中：a>0，b>0为超螺旋增益；z为姿态角二阶导数的估计值.

至此可以得到本文设计的全阶终端滑模姿态控制器如下所示

(12)

3 仿真验证

仿真时，初始高度30 km，初始飞行速度是2 800 m/s，初始姿态角Ω(0)=[0° 1° 0°]T，姿态角给定指令Ωc=[3° 0° 2°]T，初始姿态角速度p(0)=q(0)=r(0)=0(°)/s. 舵面偏转角限制在±30°. 为进一步验证所设计的姿态控制器在受扰时的鲁棒性，设大气密度摄动±20%，转动惯量摄动±10%，并外部干扰力矩为

[1+sin(πt)+sin(0.5πt)][111]T×105N·m.

仿真中的参数设置如下.

控制器参数：θ=0.6，d=20，η=3，kd=kT=1. 鲁棒微分器参数：a=2，b=4.

3.1 情况A

为了比较本文所提出的滑模控制算法与原有限时间控制算法在鲁棒性方面的改进，仿真分为以下两种情况(此时的切换控制项采用的是边界层加滤波器技术消抖的方法)：

① 在未加任何扰动时，分别对控制器(4)和控制器(12)进行仿真；

② 系统中存在参数摄动以及外部干扰，分别对控制器(4)和控制器(12)进行仿真.

图1给出了在没有外界扰动和参数摄动时分别使用控制器(4)和(12)进行仿真的姿态角跟踪曲线和舵面偏转角曲线. 由图1可知，此时两个控制器的控制效果一样，均使姿态角误差在有限时间内收敛到0，保证了跟踪精度.

图2给出了在情况 A的第2种情况下分别使用控制器(4)和(12)进行仿真的姿态角跟踪误差曲线. 由图2可知，存在外界扰动以及内部参数摄动时，本文设计的控制器式(12)具有更好的跟踪效果以及控制精度.

3.2 情况B

为了比较本文所用的抑制滑模控制器输出抖振的方法的有效性，进行如下仿真：

① 切换控制项使用饱和函数，未加滤波器；

② 切换控制项使用饱和函数加滤波器.

图3，图4分别是在情况 B的情形下进行的仿真. 由图3，图4可知，当滑模切换控制项使用符号函数时控制舵面的输出会存在较为剧烈的抖振，且在控制初始阶段存在控制量跳变；而当切换控制项使用饱和函数加滤波器时，控制舵面的输出效果最好，即控制输出较为平滑. 因此，本文采用边界层与滤波器技术相结合的方法有效抑制了滑模控制中存在的抖振问题.

4 结 论

本文对再入飞行器的姿态角跟踪控制问题进行了分析以及讨论. 通过对其模型进行简化处理以及输入输出线性化，得到了一个易于分析的对象模型. 在此基础上，完成了以下的工作：① 设计了新的终端滑模面，基于此滑模面提出了一种全阶非奇异终端滑模姿态控制算法，保证了姿态角跟踪误差在有限时间内收敛到0；② 所设计的新的终端滑模控制算法避免了传统终端滑模中存在的控制输出奇异的问题，提高了控制系统的性能；③本文通过将边界层技术与低通滤波器相结合，由仿真可知该算法消除了滑模控制中固有的抖振问题.

[1] Xu H， Mirmirani M D， Ioannou P A. Adaptive sliding mode control design for a hypersonic flight vehicle[J]. Journal of Guidance， Control， and Dynamic， 2004，27(5):829-838.

[2] Wang L， Liu X D， Cheng Y Z. High-order sliding mode observer based adaptive time-varying sliding mode for re-entry attitude control[J]. Control and Design， 29(2):281-286.

[3] Geng Jie， Sheng Y Z， Liu X D. Finite-time sliding mode attitude control for a reentry vehicle with blended aerodynamic surfaces and a reaction control system[J]. Chinese Journal of Aeronautics， 2014,27(4):964-976.

[4] Sun H B， Li S H， Sun C Y. Finite time integral sliding mode control of hypersonic vehicle[J]. Nonlinear Dyn， 2013，73(1-2):229-244.

[5] Yu X H， Man Z H. Model reference adaptive control system with terminal siding modes[J]. International Journal of Control， 64(6):1165-1176.

[6] Feng Y， Yu X H， Han F L. On nonsingular terminal sliding mode control of nonlinear system[J]. Automatic， 2013(49):1715-1722.

[7] Man Z H， Yu X H. Terminal sliding mode control of MIMO linear systems [C]//Proceedings of the 35th IEEE Conference on Decision and Control. [S.l.]: IEEE， 1996:4619-4624.

[8] Wu Y Q， Yu X H， Man Z H. Terminal sliding mode control design for uncertain dynamic systems[J]. Syst Control Lett， 1998，34(5):281-287.

[9] Feng Y， Yu X H， Man Z H. Non-singular terminal sliding mode control of rigid manipulators[J]. Automatic， 2002，38(12):2159-2167.

[10] Ackermann J， Utkin V I. Sliding mode control design based on Ackermann’s formula[J]. IEEE Trans Automat Cont， 1998，43(2):234-237.

[11] Ha Q P， Trinh H， Nguyen H T. Dynamic output feedback sliding mode control using pole placement and linear functional observers[J]. IEEE Trans Ind Electron， 2003，50(5):1030-1037.

[12] Levant A. Sliding order and sliding accuracy in sliding mode control[J]. Int J Control， 1993，58(6):1247-1263.

[13] Levant A， Fridman L. High order sliding modes: sliding mode in control engineering[M]. New York: Marcel Dekker Inc， 2002:53-101.

[14] Utkin V. Sliding modes in control and optimization[M]. Berlin， Germany: Springer-Verlag， 1992.

[15] Levant A. Robust exact differentiation via sliding mode technique[J]. Automatica， 1998，34(3)：379-384.

[16] Kang B P， Ju J L. Sliding mode controller with filtered signal for robot manipulators using virtual plant controller[J]. Mechatronics， 1997，7(3):277-286.

[17] Van Soest W R， Chu Q P， Mulder J A. Combined feedback linearization and constrained model predictive control for entry flight[J]. Journal of Guidance， Control， and Dynamics， 2006，29(2):427-434.

[18] Bhat S P， Bernstein D S. Finite-time stability of continuous autonomous systems[J]. SIAM J Control Optim， 2000,38(3):751-766.

[19] Levant A. Robust differentiation via sliding mode technique[J]. Automatica， 1998，34(3):379-384.

(责任编辑：李兵)

Robust Exact Differentiator Based Full-Order Nonsingular Terminal Sliding Mode for Re-Entry Attitude Control

LAI Ru， JIN Zhen， SHENGYong-zhi， LIU Xiang-dong

(School of Automation, Beijing Institute of Technology, Beijing 100081, China)

Considering the reentry vehicle with strong inherent coupling and highly nonlinear, a full-order nonlinear terminal sliding mode control scheme was proposed based on terminal sliding mode and robust exact differentiator (RED). Firstly, a novel full-order nonsingular terminal sliding mode control function was designed so that the derivatives of terms with fractional powers could not appear in the controller. Thus the control singularities could be avoided. Moreover, the tracking errors could be converged to 0 in finite time. Then, to obtain the derivatives of the angular velocity signal in the sliding mode manifold, a super-twisting algorithm (STA) was applied as robust exact differentiator. The interfering noise magnified with the common differentiator could be avoided because of the robustness of the RED. Furthermore, the filter and boundary layer technique were combined to alleviate chattering of the sliding mode controller. Finally, simulations were provided for the reentry vehicle with uncertain parameters and external disturbances to illustrate the effectiveness and robustness of the attitude control system.

full-order terminal sliding mode; singularity elimination; chattering alleviation; robust exact differentiator (RED); attitude control

2015-08-03

国家自然科学基金资助项目(11402020，11372034)

赖汝(1962—)，女，博士，副教授，E-mail：lairu@bit.edu.cn；金震(1990—)，男，硕士，E-mail：2120130929@bit.edu.cn.

TP 273

A

1001-0645(2016)12-1264-06

10.15918/j.tbit1001-0645.2016.12.011