微谐振器纵向振动热弹性耦合分析

李长龙， 高世桥， 牛少华， 刘海鹏

(北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

微谐振器纵向振动热弹性耦合分析

李长龙， 高世桥， 牛少华， 刘海鹏

(北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

对微谐振器在纵向振动时的热弹性耦合进行分析，以悬臂梁为基础，在环境温度为300 K时，对热弹性本构方程进行数值求解，对在纵向振动过程中产生的温度、受热弹性耦合的影响产生的频率漂移、热弹性阻尼进行分析. 分析结果发现，在纵向振动过程中，悬臂梁在前3阶振动模态下，温度变化量随着振动模态的升高而增大，在3阶振动模态时，温度变化量约为1.5 K；受热弹性耦合影响，频率漂移比首先随着梁长的增加而迅速增加，然后稳定在1.67×10-4附近；热弹性阻尼最大值约为1.0×10-4. 然后，使用COMSOL Multiphysics 软件对悬臂梁进行热弹性耦合仿真，并对数值结果进行验证. 结果表明，仿真结果与理论计算结果相吻合.

微陀螺仪； 纵向振动；热弹性耦合；频率漂移；COMSOL

在MEMS领域，设计具有高品质因子或低能量损耗的谐振器是设计MEMS器件的关键因素. 在微机械能量损失机制中存在外部能量损耗与内部能量损耗两种主要形式. 外部能量损耗如空气阻尼，是由于在非真空环境中，周围环境气体与器件相互作用而导致的能量损失[1]. 内部能量损耗包括晶格缺陷、热弹性阻尼等，主要是由于材料的内耗造成[2-3]. 随着MEMS封装技术的发展，气体阻尼对MEMS器件的影响越来越小. 内部能量损耗成为影响MEMS器件性能的主要机制. 在内部能量损耗中，热弹性阻尼成为限制高品质因子的微谐振器的主要因素.

热弹性阻尼是由谐振器在振动过程中拉伸和压缩产生的不可逆的热流而导致的. 材料在拉伸应力下温度升高，而在压缩应力下温度降低. 在材料内部形成温度梯度，为实现结构的热平衡，需要能量去调节温度梯度. 用来调节热平衡的能量是由机械能转化而成，而且这种转化是不可逆的. 在调节内部热平衡时能量损失的过程称为热弹性阻尼[4]. 只要材料的热膨胀系数不为零，在结构振动时就会有热弹性阻尼的存在. 因此，热弹性阻尼的研究成为MEMS器件阻尼研究的重点之一.

目前，关于热弹性阻尼，国内外一些学者已经对其进行了研究. Zener[5]最初引入热弹性阻尼的概念，并提出黏弹性固体中热弹性弛豫时间的概念.

Lifshitz及Rouckes[6]对Zener的理论进行了修正，推导出热弹性阻尼的精确解，

本文基于上述分析，对微谐振器在纵向振动过程中的热弹性损耗进行了研究. 本文以微陀螺仪敏感元件-悬臂梁为基础，首先建立热弹性耦合的控制方程；其次，分析悬臂梁在纵向振动过程中的温度分布、热弹性阻尼和由于热弹性耦合造成的谐振频率的漂移；最后对其进行建模，利用COMSOLMultiphysics进行仿真分析，并对理论推导的值进行验证.

1 热弹性耦合控制方程

陀螺模型如图1所示，将驱动梳齿简化成悬臂梁模型，如图2所示，尺寸为0≤x≤l,-b/2≤y≤b/2. 梁的长度方向为x轴，宽度和厚度方向分别为y和z轴. 悬臂梁最初处于零应力应变状态，并且梁上温度处为T0.

由热弹性体本构方程及热力学傅里叶定律可得热弹性耦合方程为［11］

(1)

式中：T为温度；cV为比定容热容；λ,μ为拉梅常数.

方程(1)为各向同性体三维热弹性耦合方程. 使用耦合方法解方程，评估热弹性耦合对悬臂梁纵向振动的影响. 微陀螺采用的是细长梁，根据欧拉-伯努利梁理论，假设微梁在纵向振动过程中横截面积保持为平面，并且忽略横向变形. 对于纵向振动问题，所以得变量都依赖于x轴. 将纵向振动时应变与位移的关系εx=∂ux/∂x，εy=-ν∂ux/∂x，εz=-ν∂ux/∂x代入到方程(1)中得

(2)

假设温度和位移都是时间谐振形式:

(3)

式中θ为温度变化量.

将方程(3)带入到(2)中，得

(4)

对方程(4)进行变换可得位移的偏微分方程.

(5)

其中

对偏微分方程(5)进行求解，得

(6)

式中：±rm(m=1，2)是方程Ar4+Br2+C=0的根；Lm，Nm(m=1，2) 为常数.

温度的变化量为

(7)

其中hm=

将边界条件分别代入位移与温度方程可得出关于频率的方程为

(8)

方程(8)是超正定方程，通过求解以上方程，可以求得热弹性耦合下的固有频率ω.

以上通过耦合方法计算出微梁在纵向振动时的温度变化与热弹性阻尼，下面根据非耦合方法计算悬臂梁在振动过程中的温度变化和能量损耗. 对于Si材料，热弹性耦合系数为10-5量级，意味着悬臂梁的弹性振动非耦合运动方程可以用来求解位移和温度. 悬臂梁纵向振动的位移为

(9)

(10)

悬臂梁的热边界条件为固定端绝热，自由端等温.

将机械边界条件代入到式(9)中得

(11)

纵向振动位移为

(12)

将式(12)代入到式(4)中的热动态方程得

(13)

推导出在纵向振动过程中的温度变化为

(14)

其中A，B为常数，

将热边界条件代入式(14)，得A=B=0，则

(15)

假设在每个振动周期内损失的能量全部是由调节热传导引起的，即损耗的能量都转化为热能，则损失的能量为

(16)

每个振动周期内的机械能为

(17)

悬臂梁在纵向振动过程中的热弹性阻尼为

(18)

纵向振动时热弹性阻尼与梁长的关系为

(19)

2 数值计算

陀螺仪所采用的材料为Si，环境温度为300 K. 在数值计算与仿真中的参数值如表1所示.

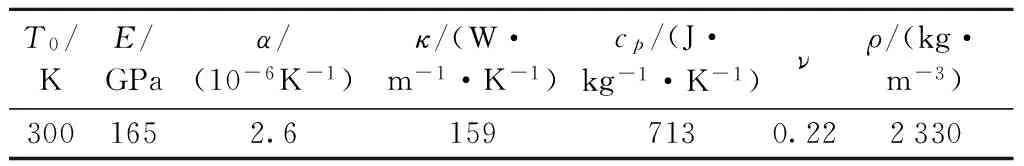
表1 各物理参数的定义

纵向振动时梁在不同位置处的位移与温度值如图3所示. 从图中看出温度在悬臂梁的固定端达到最大值，在自由端为0. 并且在前3阶振动模态下，温度变化量随着振动频率的升高而增大，在3阶模态时，温度变化量增加到1.5 K左右.

由于振动过程中温度的产生，则梁的固有频率产生漂移. 频率漂移比δ=(ωr-ω)/ω如图4所示. 其中ωr通过对方程(12)进行数值解得出. 由图可见，频率漂移比随着梁长的增加而增加，最初迅速上升，随着梁长的增加，频率漂移比逐渐趋于水平值，近似于1.67×10-4. 由此得出频率漂移比是尺度相关的参数，随着梁长的增加，温度对其影响逐渐降低并趋于稳定. 结果表明温度对振动的稳定性造成影响，并导致微结构刚度产生变化，使得固有频率产生漂移.

图5所示为悬臂梁热弹性阻尼与频率的关系，最大值为9.89×10-5，此时频率为7×1011Hz. 图6为热弹性阻尼在不同固有频率处的热弹性阻尼.

从图6可以得出，在不同固有频率时，热弹性阻尼具有相同的最大值，约为10-4，但热弹性阻尼最大值时的梁长随着固有频率的升高而增加.

对由非耦合方法和耦合方法计算得出的热弹性阻尼进行对比，结果如图7所示.

从图中可以看出，两种方法计算出的结构彼此类似，在极值点处，由耦合方法计算得到的热弹性阻尼比非耦合方法计算的值较小. 是由于使用非耦合方法，不考虑弹性振动和温度的相互耦合作用，忽略了热弹性耦合项.

3 有限元仿真

利用COMSOL多物理场耦合软件对悬臂梁进行热弹性有限元仿真，微梁模型长宽厚分别为595，30，5 μm，自由端为热绝缘，其他端面为热等温状态. 图8为前3阶纵向振动仿真结果. 从仿真结果可知，温度在固定端达到最大值，并且随着振动模态的增高而增加. 云图代表在振动时的温度分布.

为分析微梁不同位置处的温度分布，对悬臂梁进行路径分析，选取微梁不同路径，结果如图9所示.

由图9可知，1阶模态时，悬臂梁温度从固定端到自由端温度连续变化并逐渐降低，在自由端为0. 由于自由端处于热等温状态，与外部存在热交换，自由端一直处于热平衡状态. 在高阶频率处，温度发生正弦变化. 纵向振动时，固定端温度升高约3 K，不同固有频率处，固定端温升存在较小的扰动.

分别计算无耦合时的固有频率ω，热弹性耦合时的固有频率ωr，得出频率漂移比以及热弹性阻尼与梁长的关系. 结果如图10所示.

由图10可知，仿真得出的频率漂移比与理论计算值有类似的结果，稳定在1.8×10-3. 热弹性阻尼最大值约为2.2×10-4，与理论计算结果吻合.

4 结 论

本文对悬臂梁在环境温度为300 K时，纵向振动情况下的能量耗散情况进行了分析. 采用理论与仿真的方法对热弹性损耗机制进行研究，结果发现：

① 在低频振动时，温度变化量沿着x方向逐渐降低，在自由端变化量为0. 热弹性阻尼在低频下随着频率的升高而增加. 纵向振动情况下，当振动频率达到临界频率约为7×1011时，热弹性阻尼达到最大值，最大值为9.89×10-5. 当超过临界频率在高频振动时，热弹性阻尼随着频率的增加而减小.

② 在纵向振动时，不同振动模态下，由振动产生的温度约为3 K左右，振动模态不同，悬臂梁固定端的温度扰动不同.

③ 在环境温度为300 K时，经计算和仿真得知，热弹性阻尼随着梁长的增加而升高，当超过一定长度时，随之增高而降低，因此，可以通过调节梁的几何尺寸来调节热弹性阻尼.

[1] 吴衍记，黄显林.闭环光纤陀螺标度因数的温度稳定性研究[J].北京理工大学学报，2007，27(6)：618-620.

Wu Yanji， Huang Xianlin. Study on temperature stability of scale-factor in closed-loop fiber optical gyroscope[J]. Transactions of Beijing Institute of Technology， 2007，27(6)：618-620. (in Chinese)

[2] Srikar V T， Senturia S D. Thermoelastic damping in fine-grained polysilicon flexural beam resonators[J]. Journal of Microelectromechanical Systems， 2002，11(5):499-504.

[3] 董宏发，楼仁海.开式谐振腔Q值的计算与测量[J].北京理工大学学报，1988,8(4)：54-63.

Dong Hongfa， Lou Renhai. Calculation and measurement of the Q factor of an open resonator[J]. Transactions of Beijing Institute of Technology， 1988,8(4)：54-63. (in Chinese)

[4] Younis M I. MEMS linear and nonlinear statics and dynamics: MEMS linear and nonlinear statics and dynamics[M]. [S.l.]: Springer， 2011.

[5] Zener C. Internal friction in solids. I. theory of internal friction in reeds[J]. Physical Review， 1937，52(3):230-237.

[6] Lifshitz R， Roukes M L. Thermoelastic damping in micro-and nanomechanical systems[J]. Physical Review B， 2000，61(8):5600-5610.

[7] Jiao W， Song J， Guo F. Thermoelastic damping of micro resonators operating in the longitudinal vibration mode: In comparison with the case of flexural vibration[J]. Mechanics Research Communications， 2014，62:31-36.

[8] Guo F L， Rogerson G A. Thermoelastic coupling effect on a micro-machined beam resonator[J]. Mechanics Research Communications， 2003，30(6):513-518.

[9] Duwel A， Candler R N， Kenny T W， et al. Engineering MEMS resonators with low thermoelastic damping[J]. Journal of Microelectromechanical Systems， 2006，15(6):1437-1445.

[10] Zhang W， Turner K L. Thermoelastic damping in the longitudinal vibration: analysis and simulation[C]∥ASME 2004 International Mechanical Engineering Congress and Exposition. [S.l.]: American Society of Mechanical Engineers， 2004:145-149.

[11] 王洪纲.热弹性力学概论[M].北京:清华大学出版社,1989.

Wang Honggang. The theory of thermoelastic[M]. Beijing: Tsinghua University Press, 1989. (in Chinese)

(责任编辑：刘雨)

Analysis on Thermoelastic Damping of Micro Resonators from Longitudinal Vibration

LI Chang-long， GAO Shi-qiao， NIU Shao-hua， LIU Hai-peng

(State Key Laboratory of Explosion Science and Technology， Beijing Institute of Technology， Beijing 100081， China)

The thermoelastic coupling of micro resonators from the longitudinal vibration mode was analyzed. And constitutive equations of thermoelastic coupling were deduced based on the cantilever beam at the surrounding temperature of 300 K. The temperature resulted from longitudinal vibration, the frequency shift ratio and thermoelastic damping were analyzed. The results demonstrate that in the process of the first three longitudinal vibrations, the temperature vibration increases with the vibration modes. And in the third mode, the temperature vibration is about 1.5 K. The frequency shift ratio sharply increases with the beam length firstly, and then the curve gradually approaches the horizontal line at a fixed value close to 1.67×10-4. Peak value of thermoelastic damping is about 1.0×10-4. At last, the COMSOL multiphysics was used to simulate the thermoelastic coupling of the cantilever beam to verify the numerical results. The results show that the simulation results are coincided with the theoretical results.

micro-gyroscope; the longitudinal vibration; thermoelastic coupling; frequency shift; COMSOL

2015-06-15

国家“八六三”计划项目(2013AA041104)

李长龙(1989—)，男，博士生，E-mail:xiaolong_joy@163.com；高世桥(1961—)，男，教授，博士生导师，E-mail:gaoshq@bit.edu.cn.

O 327

A

1001-0645(2016)12-1237-06

10.15918/j.tbit1001-0645.2016.12.006