基于最优解析解的机载布撒武器弹道优化
2016-02-22单永志韦常柱孟秀云解静徐良臣
单永志, 韦常柱, 孟秀云, 解静, 徐良臣
(1.哈尔滨建成集团有限公司,黑龙江,哈尔滨 150030;2. 哈尔滨工业大学 航天学院,黑龙江,哈尔滨 150001;3. 北京理工大学 宇航学院,北京 100081;4. 中国人民解放军第二炮兵装备研究院,北京 100094)
基于最优解析解的机载布撒武器弹道优化
单永志1,2, 韦常柱2, 孟秀云3, 解静4, 徐良臣1
(1.哈尔滨建成集团有限公司,黑龙江,哈尔滨 150030;2. 哈尔滨工业大学 航天学院,黑龙江,哈尔滨 150001;3. 北京理工大学 宇航学院,北京 100081;4. 中国人民解放军第二炮兵装备研究院,北京 100094)
为解决机载布撒武器射程有限,而防空体系的拦截距离则不断增大,投弹载机被击落的风险越来越大的问题,本文建立了机载布撒武器纵向平面内滑翔飞行运动方程,并基于最优控制理论构造了约束布撒武器末端速度和飞行距离的性能指标泛函,然后根据哈密尔顿原理推导了最优滑翔弹道参数的解析形式. 通过与直接打靶+SQP算法的数值直接优化方法进行对比分析,验证了本文所研究的解析形式最优弹道参数求解方法具有更高的计算效率和精度.
机载布撒武器;最远滑翔弹道;最优控制;解析形式
机载布撒武器是一种中远程投放的制导武器,它能在敌防空火力区域之外投放、携带多种子弹药,属于高精度、模块化的多用途航空制导攻击武器[1]. 机载布撒武器主要用于攻击敌机场跑道、停机坪上的飞机、技术兵器阵地、电力设施、集群武装人员等各类面目标. 由于机载布撒武器一般无动力装置,必须依靠大升阻比弹体实现远距离滑翔攻击. 在进行滑翔弹道设计时需要考虑各种因素,如射程远、飞行时间短、终点需满足开舱抛撒子弹药条件等,同时还需要考虑工程实现的可能性,如舵面偏转角、法向过载、攻角等不宜过大. 在设计弹道时应尽可能综合考虑各种因素,从而得到能满足各方面要求的最佳弹道.
机载布撒器无动力飞行弹道一般分为3段[2]:稳定段、中制导段、末导段.
由于中制导段滑翔弹道方案决定了机载布撒武器的最大射程,因此为满足系统性能指标对射程的要求,需要研究能够实现无动力最远距离滑翔的弹道优化设计方案,以实现射程最大化. 弹道优化方法主要分为直接法与间接法[3]. 间接法是利用由变分法、极大值原理等得到的最优条件来求解动态优化问题,求解精度较高,但是需要推导最优解、存在两点边值问题并且约束处理困难等. 直接法采用参数化方法将连续空间的最优控制问题求解转化为一个非线性规划问题,通过数值求解非线性规划问题来获得最优轨迹. 相对于间接法其应用更为广泛,而且有很多不同算法,但是直接法存在计算速度慢、初值敏感度高等缺点. 无论直接法还是间接法,二者在工程应用中都存在一些问题,尤其是用于机载布撒器这类需要根据战场动态实时生成最优轨迹的快速打击武器,因此目前轨迹优化理论在机载布撒器上的应用较少.
刘莉等[4]根据布撒器的飞行弹道特点,建立了滑翔方案弹道的优化设计模型,采用优化设计方法对其进行了弹道优化设计,在此基础上针对机载投放的不确定性问题,提出了建立方案弹道数据库的解决方案,并对数据库的精度和效率进行了分析;陈琦等[5]针对滑翔制导炮弹提出一种不确定飞行环境下的弹道优化方法以降低方案弹道对各类随机干扰的敏感度,推导了不确定飞行环境下的弹道优化模型,利用Chebyshev伪谱法将弹道优化问题转换为非线性规划问题,在此基础上采用内点算法获得了方案弹道的最优解,对随机干扰有很好的抑制效果;田晓丽等[6]提出了一种滑翔增程火箭弹最优化弹道的求解算法,针对计算模型求解规模较大的问题,给出了用分布式并行集群计算服务器求解的进程调度方法.
针对机载布撒器需要动态实时生成最优弹道的需求,本文基于最优控制理论推导了机载布撒武器滑翔弹道最大射程控制参数的解析解——最优弹道倾角,然后结合准平衡滑翔条件得到对应最优弹道倾角的攻角,进而得到最大射程弹道. 仿真结果表明该方法计算速度快,并且不依赖初值,具有很强的在线弹道优化能力.
1 最优控制问题的数学描述
机载布撒武器最优滑翔弹道的优化研究过程是根据给定的技术指标,建立弹体的运动方程,并选择主要设计参数,构造性能指标泛函,运用现代控制理论求解最优参数,最终形成飞行弹道.
基于最优控制理论设计最优滑翔弹道,主要包括以下几方面问题:
① 系统的状态方程,即系统的动态描述,对于连续系统,其状态方程一般为
(1)
式中:X(t)为n维状态向量;u(t)为γ维控制向量;f[·]为n维向量函数.
② 容许的控制域,在实际问题中,控制向量u(t)往往不可能在γ维欧氏空间内任意取值,而是有所限制,即要求控制u(t)满足某一约束条件
(2)
在γ维欧氏空间中,所有满足式(2)的点u(t)的集合记为
(3)
其中U称为控制域,出自控制域U的控制u(t),即u(t)∈U,称为容许控制.
③ 始端和终端条件,应该明确始端t0、X(t0)和终端tf、X(tf)的取值范围. 如果t0、X(t0)给定,则称为固定始端;如果t0固定,X(t0)是任意的,则称为自由始端. 如果X(t0)需满足某约束条件,其取值在某一集合内
(4)
则称为可变始端. 类似地,终端条件有固定终端、自由终端和可变终端3种情况. 实际控制问题可能是它们的某种组合.
④ 性能指标,性能指标是最优化的具体体现,即要求什么状态达到最优,如能量最省、时间最短等. 对于连续系统,综合型性能指标的表达式为
(5)
2 滑翔弹道最优解析解推导
由于最优控制的解析解求解过程比较复杂,需要对弹体运动模型进行适当简化,将弹体的俯仰通道模型简化后建立状态方程组,该简化模型中包括距离、高度和速度等状态变量,模型中还包含描述过载、姿态角的方程.
(6)
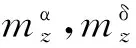
(7)
积分以外的部分为终端指标函数,即对终点的要求,被积函数为动态指标函数,这是从t0时刻到终点时刻tf整个过程中要求最优的指标. 积分号前有负号,是因为最优控制是求积分指标的最小值,加负号后代表求其最大值.
首先根据目标函数,写出哈密尔顿函数为
(8)
哈密尔顿函数只与积分号里面的项有关,与积分号外的约束项无关,为了求解最优控制规律,设置了伴随因子λ,λ为关于模型状态量y,v的动态变化的系数. 对哈密尔顿函数求相应状态变量的导数,可以得到相应的伴随方程.
伴随方程为
(9)
(10)
对积分号外的约束项求导,可以得到伴随因子λ的终端条件,得到在中段结束时λ的值.
终端条件为
(11)
(12)
(13)
伴随方程中的λy,λv必须满足终端条件,通过求解微分方程可得λy,λv的解析解. 由伴随方程和端点条件解得
(14)
(15)
其中a1为待定常数.
由于
(16)
故
(17)
对哈密尔顿函数求导,求出关于θ的H的最小值,
(18)
(19)
将θ=tan-1(λvg/v-λy)代入λ值得
(20)
其中a1为待定的未知常数,可任意取值,根据调试结果,a1可以根据c1[v-v(tf)]中的v(tf)的变化来取不同值,从而对末段速度进行约束.
由于最优弹道倾角表达式(20)是隐式表达式,所以本文采用二分法对其进行求解,最终得到最优弹道倾角θ*.
最后,基于准平衡滑翔条件
(21)
由升力系数CL得到当前弹道倾角下对应的攻角值,最终可获得最远射程滑翔弹道.
3 基于直接打靶法+SQP算法的弹道优化
为对比分析最优解析解得到的弹道,本文基于直接打靶法+SQP算法进行了机载布撒器的弹道优化,直接打靶法+SQP算法的优化模型如下:
① 控制量.
控制量为在飞行时间[0,tf]内的21个离散攻角和总飞行时间:u=[α1α2… α13tf].
② 目标函数.
即所要得到的优化弹道的性能指标(射程最远):J=-x .
③ 过程约束.
飞行过程约束主要为法向过载约束:0.5≤N≤1.5.
通过限制法向过载来控制弹道的“跳跃”程度,约束范围越宽松跳跃程度越激烈、机动范围越大,反之则否.
④ 终端约束.
飞行终端约束选为高度,令-2m≤Hf≤2m.
对终端高度进行限制主要是考虑到仿真时很难实现Hf=0,因此放宽终端高度范围.
4 仿真分析
如前文所述,调整系数c1即可得到对应于不同速度下的弹道倾角指令,进而控制飞行弹道. 由式(17)可知,系数c1越大,终端速度越接近设计速度,反之则否.
采用某型机载布撒器物理参数[7],利用第1节推导得到的最优解,终端速度设计为192m/s,令c1=1,进行投放高度6km、投放初速250m/s、弹道倾角为0°初始条件下的最大射程优化,并与基于直接打靶+SQP方法得到的最大射程弹道进行对比. 其中参考轨迹为轨迹优化初值弹道. 仿真结果如图1~图6所示.
3条轨迹参数对比见表1.
由仿真结果可以发现:
① 由于采用准平衡滑翔条件,基于最优解析解得到的弹道倾角(约为-6°,因此在t=0时刻弹道倾角有突变)及法向过载变化很小,因此相较于直接打靶+SQP方法,飞行高度与速度变化平稳;

表1 轨迹参数对比
② 基于最优解析解得到的最大射程为51.62 km,略小于SQP方法得到的射程;
③ 基于最优解析解的弹道计算时间(0.44 s)远远小于SQP方法(25.88 s).
综上可知,基于最优解析解进行轨迹优化既能得到与SQP方法相近的最大射程,又具有SQP方法所不能达到的很快的计算速度,便于弹上在线轨迹优化的实现.
5 结 论
根据最优控制理论推导了机载布撒器最大射程滑翔问题的最优性条件,利用哈密尔顿原理对最优条件进行数值求解. 仿真结果表明,基于最优控制获得解析解是快速求解机载布撒器最优滑翔弹道的一种有效方法. 本文的研究结果对其他类型的弹道优化设计有一定参考价值,对机载布撒器的总体设计及闭环近似最优滑翔制导律设计也具有重要意义.
[1] 刘晓利,陶其恒.机载布撒武器系统发展综述[J].弹道学报,1996,8(3):95-100.
Liu Xiaoli, Tao Qiheng. The development and research of the air-borne weapon dispenser system[J]. Journal of Ballistics, 1996,8(3):95-100. (in Chinese)
[2] 耿丽娜,郑志强.基于遗传算法的制导炸弹最优制导律[J].中南大学学报:自然科学版,2007,38:176-181.
Geng Lina, Zheng Zhiqiang. Optimal control law for guided bombs on genetic algorithm[J]. J Cent South Univ: Science and Technology, 2007,38: 176-181. (in Chinese)
[3] Betts J T. Survey of numerical methods for trajectory optimization[J]. Journal of Guidance, Control and Dynamics, 1998,21(2):193-206.
[4] 刘莉,李怀建. 机载布撒器滑翔方案弹道优化与方案弹道库设计[J].弹箭与制导学报,2004,21(3):61-64.
Liu Li, Li Huaijian. The project trajectory optimization of airborne dispenser and the design of trajectory database[J]. Journal of Projectiles, Rockets, Missiles and Guidance,2004,21(3):61-64. (in Chinese)
[5] 陈琦,王中原.不确定飞行环境下的滑翔制导炮弹方案弹道优化[J].航空学报,2014,35(9):2593-2604.
Chen Qi, Wang Zhongyuan. Optimal trajectory design under uncertainty for a gliding guided projectile[J]. Acta Aeronautica ET Astronautica Sinica,2014,35(9):2593-2604. (in Chinese)
[6] 田晓丽,陈国光,阚卫东.滑翔增程火箭弹弹道优化算法研究[J].应用基础与工程科学学报,2007, 15(1):137-141.
Tian Xiaoli, Chen Guoguang, Kan Weidong. Research on optimal algorithm of glide range extend rocket[J]. Journal of Basic Science and Engineering, 2007,15(1):137-141. (in Chinese)
[7] 王颖,宋龙,张拥军.制导滑翔炸弹的最优末制导律研究[J].弹箭与制导学报,2010,30(4):51-54.
Wang Ying, Song Long, Zhang Yongjun. Research on the optimal terminal guidance law for gliding guidance bombs[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2010,30(4):51-54. (in Chinese)
(责任编辑:刘雨)
Trajectory Optimization for Airborne Dispenser Based on Analytical Solution
SHAN Yong-zhi1,2, WEI Chang-zhu2, MENG Xiu-yun3, XIE Jing4, XU Liang-chen1
(1.Harbin Jiancheng Group Co. Ltd, Harbin,Heilongjiang 150030, China; 2.School of astronautics,Harbin Institute of Technology, Harbin, Heilongjiang 150001, China; 3.School of Mechatronical Engineering, Beijing Institute of Technology, Beijing 100081, China; 4.The Second Artillery Equipment Research Institute of PLA, Beijing 100094, China)
The airborne dispenser is an effective air-ground weapon possessing standoff strike ability. However its strike range is very limit, and it has to take higher risk to be intercepted with the range of air defense system increasing, so it is essential to study the theory and application of longest glide trajectory optimization for unpowered airborne dispenser. By using optimal control theory, the optimal glide flight kinematics and dynamics equations in the vertical plane were established to make performance function for final velocity and flight range control, and the analytical result of optimal glide trajectory could be obtained based on Hamilton’s principle. Compared with direct-shooting and SQP, the results show that this analytical-based method can get a optimal trajectory with a higher calculation efficiency and precision.
airborne dispenser; longest gliding trajectory; optimal control; analytical form
2015-07-16
国家自然科学基金资助项目(60217289)
单永志(1963—),男,博士,教授,E-mail:abcd@sina.com.
V 211
A
1001-0645(2016)12-1228-05
10.15918/j.tbit1001-0645.2016.12.004
