说2016届福建省高中毕业班质量检查理科综合测试第25题
2016-02-21李海彬
⌾李海彬
(作者单位:福建省南安第一中学 362300)
说2016届福建省高中毕业班质量检查理科综合测试第25题
⌾李海彬
题目:2016 届福建省高中毕业班质量检查理科综合测试第25题


(1)A第一次与挡板碰前瞬间的速度大小v;(2)A第一次与挡板碰撞到第二次与挡板碰撞的时间Δt;(3)B相对于A滑动的可能最短时间t。
一、考点分析
1、知识点:滑动摩擦力、动摩擦因数和静摩擦力属于考纲的Ⅰ级要求,牛顿运动定律、匀变速直线运动、动能定律和能量守恒属于考纲的Ⅱ级要求。2、考纲要求:能理解知识点,并能在叠加体有相对运动情景中正确运用分析,解决,推理和判断。3、命题意图:考查学生灵活应用牛顿运动定律,匀变速运动规律、动能定理、能量守恒定律解决相关问题(叠加体相对运动的问题)的能力, 考查学生的思维能力、建模能力、分析综合能力、知识迁移能力、应用数学知识解决物理问题的能力。4、考查方式:设置常见板块类叠加体模型;问题设置直接、简洁、明了。
二、学情分析
1、这是一道综合性强、过程较为复杂的问题,解决该类问题需要学生有一定的知识迁移能力和创新意识,能将实际问题转化成物理模型。对于牛顿力学,由于考生更为熟悉,也容易理解,故考生大多数用动力学的观点求解;2、思维障碍和易错点: 由于本题是多物体多过程复杂的物理问题,审题时不能精确到位,按运动过程审题及分析是学生的难点易错点。
三、解题思路
(1)B和A一起沿斜面向下运动,由机械能守恒定律有
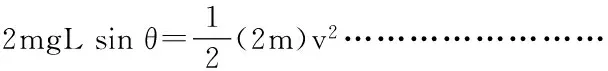

(2)第一次碰后,对B有
mg sin θ=μmg cos θ 故B匀速下滑……………………③
对A有mg sin θ+μmg cos θ=ma1……………………④
得A的加速度 a1=10m/s2,方向始终沿斜面向下, A将做类竖直上抛运动…………………… ⑤
设A第1次反弹的速度大小为v1,由动能定理有



(3)设A第2次反弹的速度大小为v2,由动能定理有
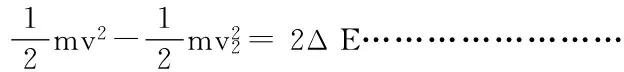
得v2=0……………………⑩
即A与挡板第2次碰后停在底端,B继续匀速下滑,与挡板碰后B反弹的速度为v′,加速度大小为a′,由动能定理有
1111mg sin θ+μmg cos θ=ma′ ………………………………(12)
当B速度为0时,因mg sin θ=μmg cos θ≤fm, B将静止在A上。……………………(14)
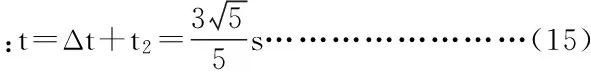
四、变式和拓展
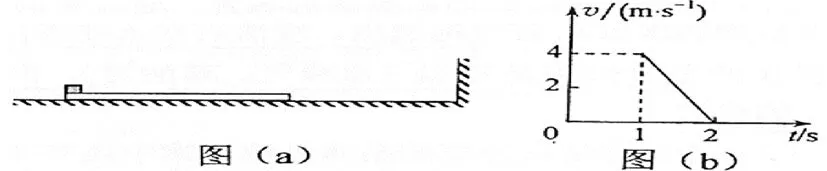
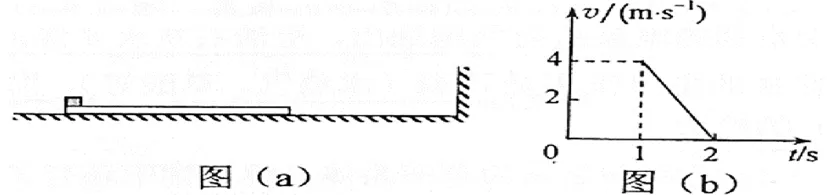
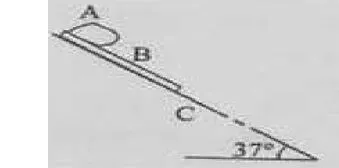
1.根据学生的能力和发展阶段可以把斜面换成光滑水平面,由简单到复杂,如:一长木板置于光滑水平地面上,木板左端放置一小物块;在木板右方有一墙壁,木板右端与墙壁的距离为4.5m,如图(a)所示。t=0时刻开始,小物块与木板一起以共同速度向右运动,直至t=1s时木板与墙壁碰撞(碰撞时间极短)。碰撞前后木板速度大小不变,方向相反;运动过程中小物块始终未离开木板。已知碰撞后1s时间内小物块的v-t图线如图(b)所示。木板的质量是小物块质量的15倍,重力加速度大小g取10m/s2.求:
(1)木板与地面间的动摩擦因数μ1及小物块与木板间的动摩擦因数μ2;(2)木板的最小长度;(3)木板右端离墙壁的最终距离。
2.再把光滑水平面换成粗糙水平面,由简单到复杂,如:(2015年新课标全国理综1卷第25题)
一长木板置于粗糙水平地面上,木板左端放置一小物块;在木板右方有一墙壁,木板右端与墙壁的距离为4.5m,如图(a)所示。t=0时刻开始,小物块与木板一起以共同速度向右运动,直至t=1s时木板与墙壁碰撞(碰撞时间极短)。碰撞前后木板速度大小不变,方向相反;运动过程中小物块始终未离开木板。已知碰撞后1s时间内小物块的v-t图线如图(b)所示。木板的质量是小物块质量的15倍,重力加速度大小g取10m/s2.求:
(1)木板与地面间的动摩擦因数μ1及小物块与木板间的动摩擦因数μ2;(2)木板的最小长度;(3)木板右端离墙壁的最终距离。


(1)A第一次与挡板碰前瞬间的速度大小v;(2)A第一次与挡板碰撞到第二次与挡板碰撞的时间Δt;(3)B相对于A滑动的可能最短时间t。
4.(2015年全国新课标Ⅱ第25题)
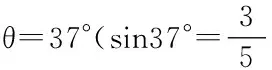
(1)在0~2s时间内A和B加速度的大小(2)A在B上总的运动时间
五、试题的创新点
它是学生“最熟悉的陌生人”。说其“熟悉”,因为这些道题目板块类叠加体模型,这种题型从高一到高三,我们不断地在练习;说其“陌生”,因为这道题目又都高于我们平常的习题,是对平常习题的延伸、拓展和创新。它呈现出信息新颖、对象多体、过程复杂、条件隐蔽、解法灵活、结果多样等特点,综合性强,能力要求高。
六、反思和感悟
平常教学中,尽量由简单到复杂,逐级加深:由单个物体单过程过渡到单个物体多过程,然后再过渡到多个物体多个过程。
解题的策略——规范分析的方法
科学的分析流程
1、明确研究对象;2、正确受力分析;3、分析运动情况
七、此题的教育功能和选拔功能
1、综合分析、逻辑推理、数学运算能力;2、联系实际解决物理问题;3、整体思维,防止顾此失彼;4、假设未知量,求解,培养前瞻意识
(作者单位:福建省南安第一中学 362300)
