高等数学的“补美法”技巧

蔡 瑾， 董 艳， 陈 琳

(1.中国人民公安大学信息技术与网络安全学院， 北京 100038； 2.成都工业学院, 四川成都 610031)

高等数学的“补美法”技巧

蔡 瑾， 董 艳， 陈 琳

(1.中国人民公安大学信息技术与网络安全学院， 北京 100038； 2.成都工业学院, 四川成都 610031)

数学不是从一开始产生就象教科书中那么完美，其往往是出于解决问题的需要，以一种直观的形式发展出来的，进而才有了数学美的简单性、统一性、对称性、奇异性的特征。本文结合高等数学中的数学定义、定理、数学知识的运用这三方面阐述了补美思想在其中的应用，阐明了高等数学教学中一种重要的学习方法——补美法。通过补美法原理的应用来激发学生追求数学美，提高学习效率、训练学生的发散思维以及培养其创新能力。

数学美； 补美法； 高等数学

0 引言

数学是理性思维和想象的结合，其历来以其高度的抽象性，严密的逻辑性为人们所赏识，却很少有人把它与美学联系起来，英国著名数理逻辑学家罗素指出：“数学，如果正常看它，不但拥有真理，而且也具有至高无上的美。” 美是科学和艺术共同追求的东西，什么是美呢？美有两个标准：一、一切绝妙的美都显示出奇异的均衡关系(培根)。二、美是各部分之间以及各部分与整体之间固有的和谐(海森伯)。数学美不同于艺术美，数学美主要表现为简单性、和谐性、统一性、对称性、奇异性。

当某一事物其内容和形式不完善时，我们往往会根据美的原理及规律去改造和完善它，这一过程中使用的方法称为补美法。数学中的补美法是建立在深刻理解数学知识的基本思想上，且必须要辅以数学美的基本原理才能实现。数学中的补美给人以完整的美感，其具有简单性、统一性、对称性和奇异性的特点，而补美法的技巧在高等数学教学中处处都有体现。高等数学中数学概念的简单性、统一性，结构系统的和谐性、对称性，数学命题和数学形式的完整性、奇异性，都是数学美的具体内容。但是只有通过补美法的应用，才能使上述特性得以实现。在教学中有意识地教给学生一种重要的学习方法——补美法，这对培养学生学习数学的兴趣，提高课堂教学效率，提高学生的数学素养有着十分重要和积极的作用。高等数学中补美法的技巧有多种类型：从不完整到完整、从规则到不规则、从不对称到对称、从无序到有序，其主要应用如下：

1 数学定义的补美

数学定义随着数学的发展会产生局限性，为改变这种情况，就必须对定义进行延拓与补充，使其更加完美。

例1 数列极限定量定义→函数极限定量定义

在讲授极限定义时，我们先从刘徽的割圆术给出了数列极限的定义：若对于任意给定的正数ε，总存在正整数N，使得对于n>N的一切xn，不等式|xn-a|<ε都成立，称常数a是数列xn的极限。数列作为特殊函数，其自变量为正整数，而对于一般的函数来说，其自变量是实数，又如何给出函数极限的定义？根据补美法“统一性”的特点，我们在理解数列极限的定义基础上，把正整数n连续化，也就是说，数列极限是n沿数轴上正整数跳跃地趋于+∞，函数极限是x沿数轴上一切点连续地趋于∞，如图1、图2所示。由此引入了函数极限的定义：如果对于任意给定的正数ε，总存在正数X，使得对适合不等式|x|>X的一切x，对应的函数值f(x)都满足不等式|f(x)-A|<ε，称常数A是f(x)当x→∞时的极限。这一定义进一步完善了极限这一体系，既符合数学美的“和谐性”又符合“统一性”，而且也让学生实实在在感受到数学美是看得见、摸得着的，并不是数学家们凭空臆造出来的。

图1 数列极限

图2 函数极限

例2 规则图形的面积→不规则图形的面积

运用初等数学知识，我们会求正多边形、圆等规则图形的面积。但在实际生活中，大量是求不规则图形的面积。如测量河流的流量，需要知道河床断面的面积；又如在设计船体时，需要计算水线面面积。这些都需讨论不规则图形的面积，即由任意曲线围成的封闭图形的面积。根据补美法“统一性及奇异性”的特点转化为求曲边梯形面积，再求两个曲边梯形面积之差——即为所求的封闭图形的面积，这样就拓展了面积的计算公式，定积分的定义应运而生。其定义采用了“分割、近似、求和、取极限”四个步骤，得到曲边梯形面积，如图3所示。

图3 曲边梯形的面积

(λ=max {Δxi})

由本例我们可以看到：依据美的规律，用补美法的“统一性及奇异性”引入定积分的定义，使求面积的方法更加完善，从而达到美的境界。

2 数学定理的补美

数学定理及其形式的简单性、完整性、对称性只有通过补美法的应用，才能使上述特性得以实现。可见，补美法是对理解数学知识的一种深入，不仅具有美学价值，更具有方法论意义。

例3 两个向量平行充分必要条件的简化

向量a=(ax,ay,az)与向量b=(bx,by,bz)平行的充分必要条件是

aybz-azby=0;azbx-axbz=0

axby-aybx=0

(1)

式(1)表达形式冗长，显然不符合数学美的“简单性”要求，根据补美法“简单性”的特点可化简为

(2)

式(2)虽然简单明了，但还不够完善，在bx，by，bz都不等于零时，式(2)和式(1)具有相同意义；但当bx，by，bz中有零时，式(2)具有局限性。根据补美法“统一性及对称性”的特点，补充规定：

(3)

式(3)代表ax=0，ay=0。这样式(2)得以完善。可见，该例中补美法的应用促进了等式的对称、整齐，既符合“简单性”又符合“对称性”的具体要求，体现了美与真的统一，进而使学生更加深入透彻的理解所学知识。

例4 正项级数极限形式比较审敛法的完善

3 数学知识运用的补美

在高等数学解题中，运用补美法，将为解题带来方便。补美法的探究与运用，不仅能训练学生的发散思维，引导他们在解题中直觉地运用补美技巧，对提高学生的数学审美能力会有所裨益。解题补美三部曲：第一步、问题难在哪里？第二步、怎样改动有利于解题？第三步、跟着感觉走。

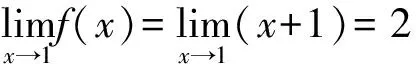
故x=1为函数第一类间断点中的可去间断点，如图4所示。问题难在哪里？x=1是可去间断点，而其它所有的点都是连续点，这样就不符合数学美的“统一性”要求，按照补美法的“统一性”补充定义：f(1)=2，即

图4 补充定义前的函数

这样一来y在点x=1处就连续了，从而在所有点都连续，如图5所示。

图5 补充定义后的函数

可见，本例x=1本来是可去间断点，但通过补美法的应用，则函数在x=1处就变得连续，实现了全体点的统一，达到美的境界，学生对可去间断点概念的印象也会非常深刻。

例6 在什么条件下，(a,b)内的连续函数f(x)为一致连续？

可见，本例是根据自身特点，挖掘美学因素，通过补美法的应用求解，达到整体的和谐与统一。

例7 设f(x)，g(x)在[a,b]上均连续，证明柯西—施瓦兹不等式

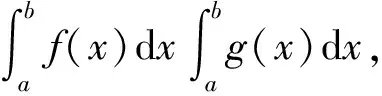
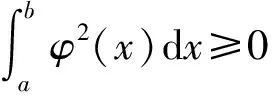
得到

最后用韦达定理即可证得。

令φ(x)=f(x)+λg(x)

则φ2(x)=f2(x)+2λf(x)g(x)+λ2g2(x)≥0

从而有

可见，本例是根据不等式内部结构，通过补美法的应用巧妙构造关系式，既满足数学结构系统的“奇异性”，又满足“和谐性”，这样学生就能掌握并熟悉这类证明题的方法。

4 结语

数学的补美是迷人的。很多复杂的数学问题，开始常常让人感觉无从下手，但是一经补充这种独特的思路，复杂的数学问题便迎刃而解，让人豁然开朗，因此在具体的高等数学教学中，对诸如上述问题，我们应该充分应用补美法的原理，引导学生在高数学习中去挖掘、去欣赏数学美，使数学变得生动、活泼、有趣，以此激发学生追求数学美，这样学生会在心灵上得到一种共鸣，在思考过程中得以尽情享受“山重水复疑无路，柳暗花明又一村”的乐趣，学习兴趣油然而生。这样一来，一方面能使学生得到一种美的享受，激发其学习兴趣，提高学习效率；另一方面对训练学生的发散思维、培养学生的创新能力、提高学生的数学审美能力等都会产生潜移默化的作用。

[1] 吴开朗. 数学美学[M]. 北京：北京教育出版社,1993.

[2] 沈山剑. 也谈数学美——补美思想的数学应用[J]. 数学通报, 1998(4):10-12.

[3] 刘玉琏. 数学分析讲义第五版[M]. 北京：高等教育出版社,2010.

[4] 同济大学数学系. 高等数学第六版[M]. 北京：高等教育出版社,2007.

[5] 吴振奎,吴旻. 数学中的美[M]. 哈尔滨：哈尔滨工业大学出版社,2011.

(责任编辑 于瑞华)

蔡瑾(1971—)，女，河北辛集人，硕士，讲师，研究方向为应用数学。

D13