需求对价格敏感情况下的库存控制与定价研究

唐艳

（深圳技师学院 国际商务系，广东 深圳 518000）

需求对价格敏感情况下的库存控制与定价研究

唐艳

（深圳技师学院 国际商务系，广东 深圳 518000）

用价格来引导需求是当前较多企业的经营策略，库存管理和定价成为该策略中的重要问题，在借鉴已有研究的基础上对该问题进行了理论研究。在单品种、需求函数为价格的二阶可导递减凹函数、可提前订货的假设下建立了动态规划模型，从理论上证明了在假设前提下最优定价策略的存在性以及在该价格策略下的补库策略。

库存控制；定价；需求随价格可变

1 引言

库存控制是企业经营的关键环节，过高的库存可能导致产品的积压，过低的库存又可能导致缺货，而传统的EOQ模型适合在假设需求稳定的情况下进行该问题的研究。但是，商业环境在不断变化，特别在当前互联网购物环境大背景下，网商为了刺激需求，相互之间的价格战是家常便饭，京东商场、淘宝、天猫每年的双十一的血拼让人记忆犹新，价格战显然是为了刺激需求，这也反映出价格的变化对需求有着明显的影响，在这种情况下需求不再是稳定的，而是可以通过价格进行调节，这便使得企业面临价格引导需求情况下的库存控制问题。同时，可以提前订货也是大部分企业能够做到的，而现在的问题是如何定价以引导需求才能使企业在综合考虑库存控制情况下使得企业整体收益最大。本文试图通过建立数学模型来从理论上探讨这样一个问题：在结合已有的理论分析基础上，在需求为价格敏感且允许顾客提前订货的情况下，企业该如何做好库存控制以及是否存在最优定价，使企业整体利润最大化。

2 文献综述

Whitin在1955年对价格引导需求情况下的单周期库存管理问题进行了研究，其研究在EOQ模型的基础上假设需求为价格的单调递减线性函数，在该假设情况下得到了最优价格以及在该价格下的最优订货量，Whitin同时还研究了需求为价格可变并带有一定随机性的库存管理问题，在假设需求为价格的线性函数的情况下引入服从U(0，2)的随机变量并得出了相应的结论。Howard Kunreuther和Jean Francois Richard在1971年也对需求为价格函数的单周期库存管理问题进行了研究，其研究得到的结论是在价格影响需求的假设下，企业将价格与库存综合考虑进行决策将获得更高的利润。Wagner和Whitin在1958年对该问题的多周期问题进行了研究，通过建立动态规划模型讨论了需求为价格函数情况下的定价及库存控制问题。Bhattacharjee和Ramesh在2000年也对该问题进行了研究，并研究了该问题的启发式算法。Federgruen和Heching在2002年研究了需求随价格可变并带有一定随机性情况下的库存管理问题，假设可延迟交付、库存费用或缺货费用为凸函数、单周期库存费用为价格和库存水平的联合凹函数。假设需求为价格的函数，但允许顾客提前订货并通过远期定价来增加需求的确定性，该假设更接近于当前的交易环境，Sumit Kunnumkal和Huseyin Topaloglu在2008年对该问题进行了研究。

3 模型建立及相关结论的证明

3.1 模型假设

（1）经销商只经营一种货物，允许顾客提前订货，每周期进行库存盘点并在周期初决策下一周期的订货量以及未来若干周期的价格。

（2）需求为价格的函数，该函数满足：单调递减、二阶可导凹函数，需求函数受到的外界随机扰动期望值为零。

（3）库存费用及缺货费用为每周期末库存的凸函数。

3.2 模型建立及相关结论与证明

设在第t周期初，需要确定未来N周期的价格，设订购在s周期交付货物的价格为在该价格下，设需求函数为根据假设2，xt(pt,s)为二阶可导凹函数，且Eε=0。

选取该院疗养的2 000例糖尿病疗养员作为研究对象，其中男1 325例，女 675例，年龄 40～78岁，平均(59.73±8.49)岁，病程 3～20 年，平均(11.65±3.86)岁；以同期在我院接受健康体检的500名健康人群作为健康对照组，其中男316名，女184名，年龄41～80岁，平均(60.36±8.72)岁；两组受检者在性别分布、年龄等一般资料方面差异无统计学意义(P＞0.05)，具有可比性。

在第t周期初已知的s周期的总需求为：Ds,t=在确定价格为pt,s后，又会产生新的需求

设供应商订货提前期为L，当前库存为it，延期交货量为Yt，补货量为Bt，在t到t+L周期内，补库前的总库存为补库后库存为It，则：

在t到t+L周期内的需求为补库前库存为补库后库存为It=I1t+Bt=

在t周期初，提前期外各周期需求为向量：设N＞L+1。

在t周期初，需要做出的决策是：当前周期的补货量Bt以及s周期交付所对应的订货价格pt,s（其中s=t,t+1,…,t+N）。所面对的状态变量是和Dt。状态转换关系为：

在第t周期，库存费用或缺货费用设为Ht(It,pt)=其中ht为凸函数且也既有同时假设费用函数为多项式有界函数。即：存在整数α，使得：

设每次订货的固定费用为Gt，单位订货费用为Ct，由此，可以计算在周期t内的收益函数为

证明如下：

以下建立动态规划模型：

设在t阶段状态变量为从t阶段到T阶段的最大期望收益为则可得动态规划模型为：

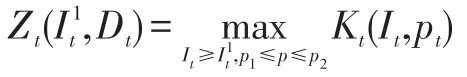
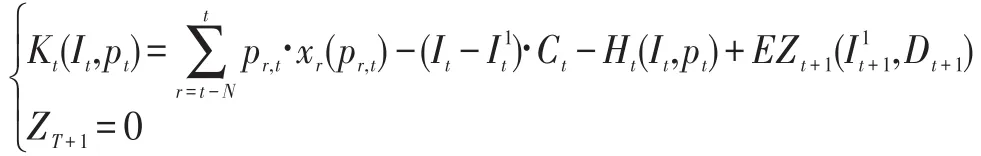
对该动态规划模型，可证明如下结论：

（2）对∀t，有且存在最大值点。

采用归纳法来证明。证明如下：

对（1）的证明：t=T时，有由结论一，Kt为关于It和pt的联合凹函数，所以为关于的单调递减凹函数。假设在t周期结论成立，则在t-1周期时，由其中为关于和的联合凹函数，由假设为关于的单调递减凹函数为关于和的联合凸函数，为单调递减函数，所以为关于和的联合凹函数，再回到前述等式，容易知道原结论成立。

对（2）的证明：t=T时，有由假设费用函数为多项式有界函数。即：存在整数α，使得：由前述证明，KT为凹函数，且所以KT存在最大值点，设为由有

设在t周期结论成立，即存在最大值点且Zt和Kt都为关于IT和有界。则在t-1周期，由（1）有即存在常数U＞0,使得因为故有：

即有：

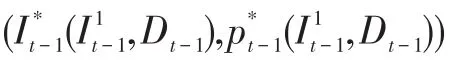
由此，可以得出如下结论：

在t周期初，在需求为Dt的状态下，存在最大值点当补库至当无需补库。具体证明如下：

对周期t，由为凹函数且存在最大值点则对任意需求Dt，由为凹函数，且故存在最大值点，记为：所以，当时为最优决策，即补充库存至且最优定价为当时，最优策略为不补库，即

4 结束语

针对需求对价格敏感的库存控制与定价问题，本文建立了动态规划模型来进行研究，在假设前提下证明了最优价格策略的存在性以及相应的补货策略。当然，相关讨论还可以继续深入，比如本文没有考虑固定费用，也相当于假设固定费用为零，固定费用可以在后续研究中加入，本文中的一些假设也可以进一步放宽，从而更进一步的符合实际情况。这些都可以在后续研究中继续讨论。

[1]M F Keblis,F Youyi."Optimal pricing and production control in an assembly system with a general stockout cost[J].IEEE transactions on automatic control,2012,57(7):1 821-1 826.

[2]L Chen,Y Chen,Z Pang.Dynamic pricing and inventory control in a make-to-stock queue with information on the production status[J].Automation Science and Engineering,IEEE Transactions on,2011,8(2).

[3]Yano C A,Gilbert S M.Coordinated pricing and production/ procurement decision:A review[A].In A Chakravarty,J Eliashbert(eds),Managing business interfaces:Marketing,engineering and manufacturing perspectives[C].Amsterdam:Kluwer Academic,2002.

[4]Chao X,Chen H,Zheng S.Joint replenishment and pricing decisions in inventory systems with stochastically dependent supply capacity[J].Eur J Oper,Res,2008,191(1):142-155.

[5]Chen H,Zhang Z.Joint pricing and inventory control with general additive demand[A].Joint CORS/INFORMS Internat.Conf [C].Toronto,2009.

[6]Chen X,Simchi-Levi D.Coordinating inventory control and pricing strategies with random demand and fixed ordering cost:The finite horizon case[J].Operations Research,2004,52: 887-896.

[7]Elmaghraby W,Keskinocak P.Dynamic pricing in the presence of inventory considerations:Research overview,current practices and future directions[J].Management Science,2003,49 (10):1 287-1 309.

Study on Inventory Control and Pricing with Price-sensitive Demand

Tang Yan
(Department of International Business,Shenzhen Institute of Technology,Shenzhen 518000,China)

In this paper,based on previous studies,we analyzed theoretically the inventory management and pricing in enterprise operation strategy,built the dynamic programming model on the premises of single product,the demand being a secondary derivable decreasing concave function of price,and advance order allowed,and proved theoretically the existence of an optimal pricing strategy against such premises as well as the corresponding replenishment strategy for it.

inventory control;pricing;demand varying with price

O227;F253

A

1005-152X(2016)12-0101-03

10.3969/j.issn.1005-152X.2016.12.024

2016-10-24

唐艳（1983-），女，华东交通大学物流工程硕士，深圳技师学院讲师，研究方向：供应链管理、物流与营销专业教学。