大型工程结构失稳问题的数值模拟研究及预防措施

2016-02-20王思晨车金如

河北能源职业技术学院学报 2016年4期

关键词：构件稳定性钢筋

王思晨，陈龙，石健，齐晖，车金如

(宁波工程学院，浙江宁波 315211)

大型工程结构失稳问题的数值模拟研究及预防措施

王思晨，陈龙，石健，齐晖，车金如

(宁波工程学院，浙江宁波 315211)

大型工程结构坍塌事故频发，结构失稳破坏是其主要原因。结构整体失稳往往是由于结构中个别构件发生强度、刚度及失稳破坏而引起。本文针对单个构件失稳破坏引发结构失稳问题，从理论计算和数值模拟两方面给出钢筋混凝土结构细长受压柱的临界荷载，分析结构失稳的原因并给出预防措施。

结构失稳；数值模拟；力学模型

1.引言

1.1 结构失稳概念

工程结构或其构件除了应具有足够的强度和刚度外，还应有足够的稳定性，以确保结构的使用安全。结构的稳定性是指结构在荷载作用下，保持原有平衡状态的能力。在工程实际中曾发生过众多由于结构失稳而造成破坏的工程事故。其中有19世纪末被称为“工程师之戒”的加拿大魁北克大桥的坍塌，还有二十世纪末发生在我国重庆市綦江县彩虹桥整体垮塌等，凡此种种都为我们敲响了警钟。所以研究结构及其构件的稳定性问题，与研究其强度和刚度具有同样重要性。

结构物及其构件在荷载作用下，外力和内力必须保持平衡，稳定分析就是研究结构或构件平衡状态是否稳定的问题。当结构或构件处于不稳定平衡状态时，任何微小的干扰都会使结构或构件发生很大的变形，从而丧失承载能力，这种情况称为失稳，或称为屈曲。

1.2 结构失稳的分类

结构稳定问题可分为两类：

1.2.1 质变失稳—结构失稳前的平衡形式为不稳定，出现了新的与失稳前平衡形式有本质区别的平衡形式，结构的内力和变形都产生了突然性变化，这种失稳称为第一类失稳，结构丧失第一类稳定性又称为分支点失稳。

1.2.2 量变失稳—结构失稳时，其变形将大大发展(数量上的变化)，而不会出现新的变形形式，即结构的平衡形式不发生质的变化，这种失稳称为第二类失稳，结构丧失第二类稳定性又称为极值点失稳。

1.2.3 研究失稳的意义

结构无论是丧失第一类稳定性还是第二类稳定性，对于工程结构来说都是不能容许的。结构失稳以后将不能维持原有的工作状态，甚至丧失承载能力，而且其变形通常急剧增加导致结构破坏。因此，在工程结构设计中除了要考虑结构的强度外，还应进行其稳定性校核。

据统计，我国每年因大型工程结构失稳而导致的经济损失就多达数千万元。为了掌握大型工程结构失稳机理，对大型工程结构失稳的事故做到提前预防，进一步完善预防手段，以便采取主动应对措施。通过对现有大型工程失稳事故发生、发展和预防等展开调查研究，便于掌握其发生的规律，依此提高工程界对失稳问题的理解、认识和重视。应用力学知识、材料知识、结构知识和稳定理论等，以宁波工程学院建工实验中心现有设备为依托，借助结构计算室大型有限元软件，对已发生工程失稳案例进行数值模拟，通过工程模型简化，现场数据搜集，对已发失稳事故进行计算机模拟，给出有效的数值计算方法，为现场提供一整套积极预防措施。

2.结构失稳破坏的调查与分析

通过对失稳结构的实地调查，发现以下问题：

2.1 结构失稳的特征

从观测可知结构失稳具有以下特征：

结构中有个别构件处于应力较高水平，易发生结构失稳现象。结构失稳具有突发性，是一个动力学过程。结构失稳时，结构产生很大位移并且发生瞬间坍塌。

2.2 结构失稳的假设

基于现场观察和理论研究，对结构失稳提出以下假设：

结构在尚未达到临界状态时，处于平衡状态，并不因强度不够而失效；结构中的构件是均匀、连续和各向同性的，服从对应的强度理论。

2.3 结构失稳的分析

2.3.1 能量准则

在热力学第二定律基础上导出的最小二阶功原理，可用作判别失稳的准则，在有限变形的条件下，发生在结构中变形构件的二阶功是

(1)

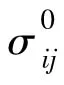
δ2W>0，表明结构的平衡状态是稳定的；δ2W<0，表明结构的平衡状态是不稳定的；它表示由于失稳，结构发生失效；δ2W=0，表明结构处于临界状态。所以，δ2W=0可用作判断线性和非线性条件下结构失稳的统一准则。

2.4 有限元方程

借助于有限元方法将结构离散化，并以矩阵形式给出的特征方程代入(1)式可得下式：

(k0+λik△)vi=0

(2)

因用于计算结构特征值的载荷水平低于结构因强度不够而产生破坏的载荷水平，故导致结构发生失稳破坏。公式中各字母的意义：k0是与初始状态有关的刚度矩阵；k△是用于失稳分析的载荷增量引起的刚度矩阵；λi和vi分别代表结构失稳的特征值和与特征值相对应的特征向量。这里仅第一特征值(最小的特征值)及其对应的屈曲模态在实践中有意义。

2.5 临界荷载的确定

钢筋混凝土结构强度高耐久性好，是工程中常用的结构之一，其中的柱构件比较细长，截面相对较小，组成构件的板件宽而薄，因而在荷载作用下容易丧失稳定性。稳定的平衡位置与不稳定的平衡位置之间的分界点称为临界点，临界点所对应的荷载称为临界荷载。工程设计中确定静定结构的临界载荷时，采用了如下习惯做法，即只要组成静定结构的构件之一失稳时，结构将失去平衡能力，此时的外载荷就是结构的临界载荷。静不定结构也叫超静定结构，它含有平衡要求之外的多余构件，称多余约束。当具有多余约束的结构(或构件)失稳时，结构(或构件)仍具有承载能力，只有当最后的静定结构也失去平衡能力时，对应的载荷才是静不定结构的临界载荷。

2.6 结构细长受压柱临界力计算

如图1所示为某住宅建筑中钢筋混凝土柱，其截面尺寸b=300mm，h=300mm，l=3000mm，混凝土强度等级为C=30，采用HRB400钢筋，As选用820(As=2513mm2)

其配筋如图1所示。

解：

计算钢筋混凝土柱的弹性模量E

EA=E1A1+E2A2(E为等效弹性模量，E1为钢筋弹性模量，E2为混凝土弹性模量，A1为钢筋面积，A2为混凝土面积)

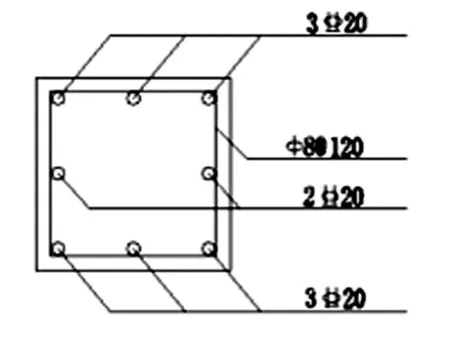
图1 柱截面尺寸及钢筋布置图

由题意可知：A=300×300=9.0×104mm2，E1=200GPa ，E2=30GPa，A1=2.51×10mm2，A2=A-A1=9.0×104-2.51×103=8.75×104

通过计算可得：E=34.7GPa

计算截面惯性矩I

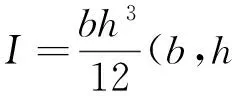
计算得：I=6.75×108mm4

细长受压柱的临界力计算

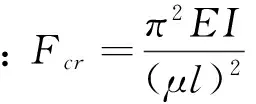
(3)

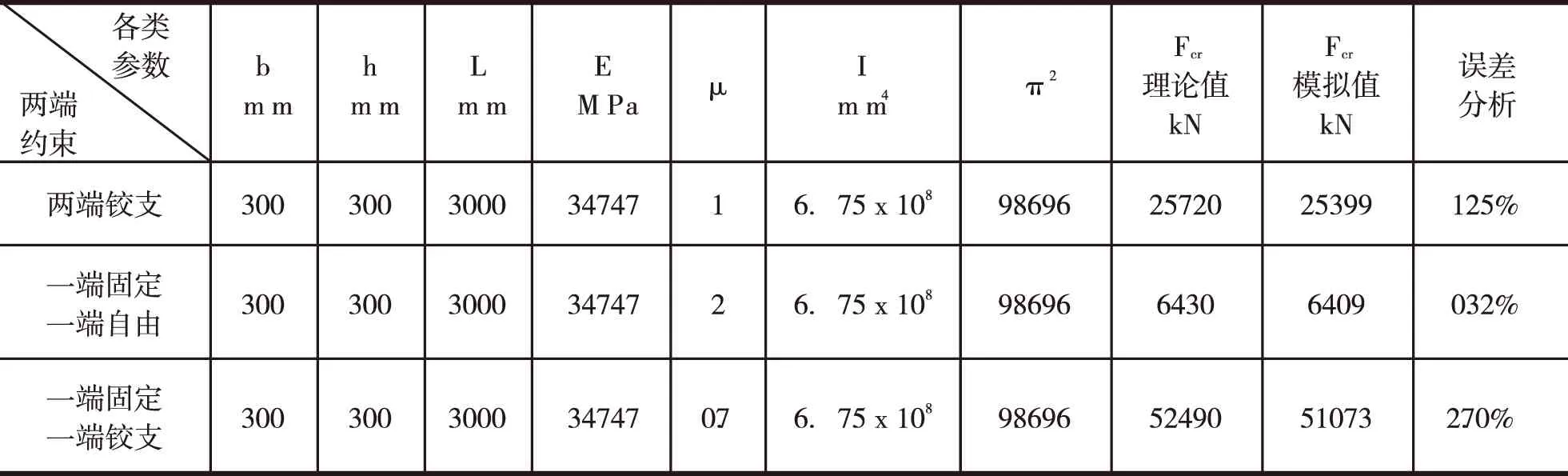
例如：当约束情况为两端铰支时，将μ=1及已上所得量代入公式(3)得：Fcr=2.75×104kN(理论值)，同理可得其他约束情况下的临界力值，参见表1。

3. 结构构件失稳的数值模拟

3.1 计算机模拟过程

1. 创建部件；

2. 创建材料属性，选择弹性(弹性模量E=34.7GPa，泊松比v=0.2)；

3. 创建截面，柱的截面尺寸为300x300(单位)；

4. 指派梁的方向；

5. 装配，创建实例；

6. 创建分析步，选择线性摄动—屈曲；

7. 创建边界条件，施加载荷；

BC-1 一端固定，一端自由

U1=U2=UR3=0 CF2=-1000

BC-2 一端固定，一端铰支

U1=U2=UR3=0 U1=0，CF2=-1000

BC-3两端铰支

U1=U2=0 U0=0，CF2=-1000

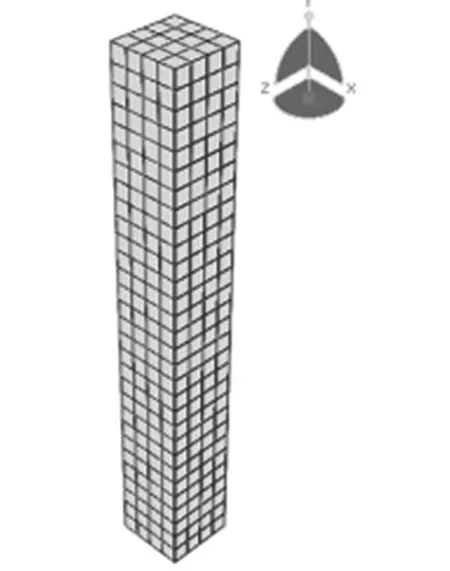
图2 柱计算机模拟图

8. 划分网格(如图2所示)；

9. 作业，检查数据，分析得出结果；

由表1不难看出，钢筋混凝土结构的细长受压柱其临界力的计算可以采用欧拉公式进行计算，其计算值与模拟值相比误差较小且屈曲模态也具有良好的对应性。

3.2 细长受压柱临界力的模拟与计算值比对

见表1。

表1 钢筋混凝土结构300×300截面受压柱不同约束下临界力的模拟与计算值比对

3.3 细长受压杆柱的屈曲模态

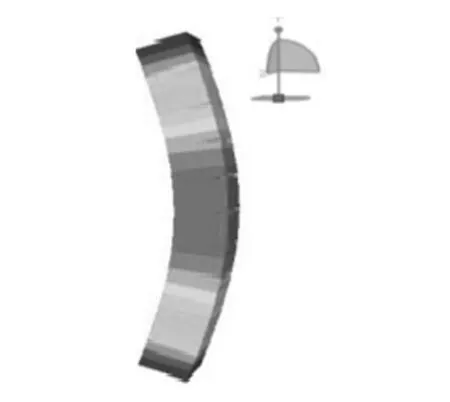
图3 两端铰支柱失稳图

图4 一端固定一端自由柱失稳图

图5 一端固定一端较支柱失稳图

4. 结构失稳的原因分析

4.1 结构整体失稳的原因分析

4.1.1 设计错误

设计错误主要与设计人员的水平有关。如：缺乏结构整体和局部失稳的概念；使用错误的失稳验算公式；只验算基本构件的稳定，忽视整体结构的稳定验算；计算简图及支座约束与实际受力不符，设计安全储备过小等。

4.1.2 工作缺陷

受压构件的制作缺陷通常包括构件的初弯曲、初偏心、热轧冷加工以及焊接产生的残余变形等。这些缺陷将对钢结构的稳定承载力产生显著影响。

4.1.3 支撑不足

钢筋混凝土结构在安装过程中，当尚未完全形成整体结构之前，属几何可变体系，构件的稳定性很差。因此必须设置足够的临时支撑体系来维持安装过程中的整体稳定性。若临时支撑设置不合理或者数量不足，轻则会导致部分构件丧失稳定性，重则造成整个结构在施工过程中倒塌或倾覆。

4.1.4 使用不当

当结构竣工并投入使用后，若使用不当或变更功能等意外因素也是导致失稳事故的主要原因。例如，使用方随意改造结构或构件的使用功能；改变构件的受力状态；由积灰或增加悬吊设备引起的超载；基础不均匀沉降和温度应力引起附加变形以及意外冲击荷载等。

4.2 结构局部失稳的原因分析

结构局部失稳主要是针对构件而言，其失稳的后果虽然没有整体失稳严重，但对以下原因引起的失稳也应引起足够的重视。

4.2.1 设计错误

设计人员忽视甚至不进行构件的局部稳定计算，或验收方法错误，致使组成构件的各类板宽厚比和高宽比大于规范限值。

4.2.2 构造不当

通常在构件局部受集中力作用的部位，原则上应设置构造加劲肋。另外，为了保证构件在运转过程中不变形也必须设置横隔、加劲肋等。但实际工程中，加劲肋数量不足、构造不当的现象比较普遍。

4.2.3 原始缺陷

原始缺陷包括钢材的负公差严重超规，制作过程中焊接等工艺产生的局部鼓曲和波浪变形等。

4.2.4 误选吊点

结构在吊装过程中，特别是大型钢结构的构件，吊点位置的选定十分重要，吊点位置不同，构件受力的状态也不同，有时构件内部过大的压应力将会导致构件在吊装过程中产生局部失稳。

5. 结构失稳的处理与防范

大型结构失稳事故需以预防为主，应遵守以下原则：

5.1 强化稳定性设计的理念

结构的整体布置必须考虑整个体系及其组成部分的稳定性要求，尤其是支撑体系的布置。结构稳定计算的假定必须符合实际受力情况，尤其是要考虑支座约束的影响。

构件的稳定计算与细部构造的稳定计算必须配合，尤其要有强节点的概念。

强度问题通常采用一阶分析，而稳定问题原则应采用二阶分析。

叠加原理适用于强度问题，不适用于稳定问题。

处理稳定问题须有整体观点，应考虑整体稳定和局部稳定的相互影响。

5.2 结构或构件的制作力求减少缺陷

在常见的众多缺陷中，初弯曲、初偏心、残余应力等对稳定承载力影响最大，因此，制作单位应通过合理工艺和质量控制措施将缺陷降低到最小程度。

5.3 施工单位应确保安装过程中的安全

对吊装结构的处理，施工单位要制定科学的施工组织设计，采用合理的吊装方案，精心布置临时支撑，以防止钢结构安装过程中的失稳，确保结构使用安全。

5.4 使用单位应正确使用钢结构建筑物

使用单位要注意对已建钢结构进行定期检查和维护，当需要进行工艺流程和使用功能改造时，必须与设计单位或有关专业人士协商，不得擅自增加负荷或改变构件受力。

[1]李丽君，沈玉凤.ANSYS对于压杆稳定的辅助教学[J].实验科学与技术，2009，01：121-122+125.

[2]董冠文，李宗义，赵彦军，王泽荫，杨龙，张庆华，杜建霞，赵典凯.压杆稳定临界力欧拉公式统一推导[J].武汉工程大学学报，2012，12：71-74.

[3]冯贤桂.细长压杆临界压力欧拉公式的统一推导[J].力学与实践，2003，04：65-67.

[4]林红，胡玉林，薛世峰.ANSYS在工科材料力学教学中的应用[J].电脑学习，2011，01：15-17.

Research on Numerical Simulation of Large Engineering Structural Instability and its Preventive Measures

WANG Si-chen, CHEN Long, SHI Jian, Qi Hui, CHE Jin-ru

(Ningbo University of Technology, Ningbo Zhejiang, 315211 China)

Large engineering structure collapse accidents are mainly caused by structural instability. The overall structural instability is often attributed to certain particular components of the structure that lead to strength, stiffness and stability failures. The paper only focuses on structural instability problems caused by a single component stability failure. It provides the critical load of reinforced concrete slender compression columns both from the theoretical calculation and numerical simulation. It also analyses the causes of structural instability and proposes preventive measures.

structural instability; numerical simulation; mechanical model