基于GPU并行计算的超声波束合成方法
2016-02-18陈胤燃罗建文
陈胤燃 何 琼 罗建文*
1(清华大学医学院生物医学工程系,北京 100084)2(清华大学生物医学影像研究中心,北京 100084)
基于GPU并行计算的超声波束合成方法
陈胤燃1,2何 琼1,2罗建文1,2*
1(清华大学医学院生物医学工程系,北京 100084)2(清华大学生物医学影像研究中心,北京 100084)
逐列扫描式的聚焦成像方法会限制超声成像帧频的提高。采用平面波发射模式只需要一次发射和接收即可获得一幅完整的超声图像,平面波成像是可以大幅度地提高成像帧频,从而实现超声超高速成像的方法之一。但是现有的超声波束合成器无法达到超声超高速成像对于计算能力的要求。对基于平面波成像的超声延时-叠加波束合成算法进行并行性分析,在此基础上设计并实现两种基于图形处理器(GPU)并行计算的超声平面波成像波束合成方法——基于2个Kernel和基于1个Kernel的并行波束合成方法。两种方法的主要区别在于波束合成中对延时值的计算和存储策略的不同处理,仿体实验证明两种方法的计算帧频分别达到2 178 和2 453 帧/s。相比于普通的方法,这两种基于GPU的并行波束合成方法的计算帧频分别提速99倍和111倍。实验结果表明,GPU波束合成器相比于传统方法,可以大幅度提高计算能力。
超声成像;波束合成;并行计算;图形处理器
引言
传统的超声B模式成像利用多次发射和接收聚焦声波来合成一幅完整的图像,该成像模式下的理论最高帧频一般在几十到一百多帧每秒之间。如果采用多焦点发射的模式,该理论最高帧频将相应降低,降低的倍数等于多焦点增加的个数。为了进一步提高超声成像的帧频,随着超声成像系统软硬件水平的不断提高,超高速超声成像逐渐发展为如今超声成像的研究热点之一。
超高速超声成像的概念最早由Bruneel等在1977年提出[1]。在1979年,和Bruneel同一个组的Delannoy等开发出了一个超声系统,可以通过一次的脉冲发射,利用模拟域的并行数据处理而获得一幅图像,该系统可以达到1 000帧/s的速度(70条线)[2]。在Bruneel和Delannoy等之后,1984年,Shattuck等在相控阵成像中通过在一次发射后同时计算多条B模式扫描线的方法来提高成像速度[3]。1991年,Lu和Greenleaf提出了基于非衍射波束的超声成像来提高成像速度[4]。从20世纪90年代开始,Fink等提出了平面波发射和并行波束合成的方法来实现超高速成像,该方法可以将帧频提高到数千帧每秒[5-7]。平面波成像在发射过程中同时激励超声探头的所有阵元,发出波前形状为平面的脉冲超声波,平面波在传播过程中覆盖整个成像区域。在接收过程中,各个阵元接收声场中的回波信号,经过并行波束合成和其他后处理之后得到一幅完整的B模式图像,平面波成像只需要一次发射/接收过程即可以获得一幅图像,因此其理论最高成像帧频为
(1)
式中,Z是成像区域的深度,c是超声波在组织中传播的速度。
通常认为c的值为1 540m/s,假设图像深度为5cm,那么对应的理论最高帧频为15 400f/s(帧/s)超高的帧频可以带来绝佳的时间分辨率,从而能够捕捉到组织运动中的更多细节,有效地辅助疾病的诊断,如实现剪切波弹性成像、超高速超声多普勒成像等。
就超声波发射/接收的环节而言,平面波成像相比于传统聚焦成像能够大幅度地提高帧频,但要真正实现超高速成像,还需要解决成像过程中因为单位时间内数据量大幅度增加而带来的计算能力不足的问题。现有临床超声设备的波束合成环节都通过数字信号处理器(DSP)、现场可编程门阵列(FPGA)等设备来实现,这些设备的计算能力还无法满足超声超高速成像波束合成实时计算的要求。
图形处理器或图像处理单元(graphicsprocessingunit,GPU),由于具有强大的数值计算能力和高度的可并行性,使得它成为通用计算领域的强大工具,也是实现超声超高速成像的工具之一。夏春兰等利用GPU实现了从超声射频(RF)信号到B模式图像的各项关键环节的处理,显著地提高了成像的速度[8]。一些学者将GPU应用于超声的波束合成,并利用多个GPU实现了平面波成像波束合成的并行处理,在一定的成像参数下,实现了每秒数千帧的计算帧频[9-12]。
本研究采用平面波成像方式和延时-叠加波束合成算法,利用一块商用GPU,采用NVIDIA公司开发的统一计算架构(computeunifieddevicearchitecture,CUDA),结合C语言进行编程[13],设计并实现了两种基于GPU并行计算的平面波成像波束合成方法。
1 方法
1.1 CUDA编程模型
1.1.1 GPU并行计算模型
在介绍CUDA架构的编程模型之前,首先了解几个和CUDA编程有关的概念[13-16]:
1) Kernel:指可以在GPU中运行的函数,也称之为内核函数,CUDA程序中需要交给GPU处理的命令都需要写在Kernel函数中,供GPU调用。
2) Grid:是一个虚拟的概念,中文名称“线程网格”或“网格”,它是一个和Kernel相对应的概念,通常一个Kernel对应着一个特定的Grid,即运行一个Kernel都需要生成一个Grid。
3) Block:中文名称为“线程块”,Block是Grid的最小执行单位,一个Grid中可以划分出多个Block,各个Block在任务中是并行执行的,Block之间没有固定的执行顺序,也不能进行通信,Grid里最多可以划分出3个维度的Block。
4) Thread:中文名称“线程”,是执行计算任务的最小单位,一个Block里可以划分出最多3个维度的Thread,同一个Block里的Thread在执行任务的时候可以通过共享存储器进行通信。
图1说明了一个Kernel中的Grid、Block和Thread之间的抽象关系,可以看出在Kernel中存在着两个层次的并行:Grid中Block之间的并行和Block中Thread的并行。
使用GPU进行并行计算时,需要根据待处理数据的具体特征,合理设计Grid和Block的维度、Grid中每一个维度上的Block数目和Block中每一个维度上的Thread数目。
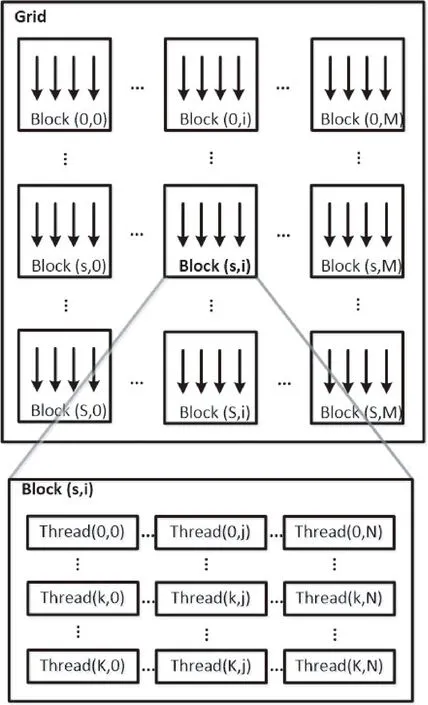
图1 一个Kernel中Grid、Block和Thread之间的抽象关系(以二维为例)Fig.1 Abstract relations of grid, block and thread in one kernel (a 2-D case)
1.1.2 GPU数据存储架构
GPU中有多种类型的存储器,它们和Grid、Block、Thread之间的读写访问关系如表1所示。
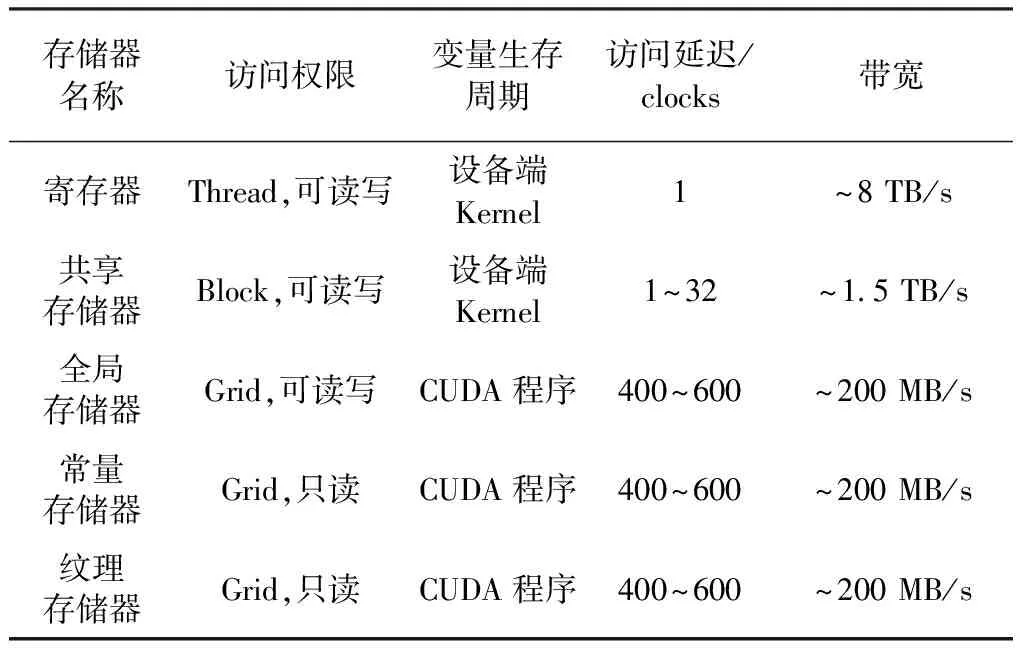
表1 GPU中各种存储器的比较 [13-16]
利用GPU进行并行计算时,数据在其中的存储策略合理与否对计算的效率有很大的影响。在进行波束合成并行计算时,需要尽可能地提高数据读写的速度。共享存储器在所有的存储器中,访问延迟较小,带宽较高,可以同时被一个Block里的所有Thread并行访问。在并行波束合成的具体实现过程中,使用共享存储器可优化数据存储策略,在一定程度上提高了波束合成的速度。
1.2 GPU并行波束合成方法设计和实现
1.2.1 延时-叠加波束合成算法并行性分析
采用延时-叠加波束合成算法,首先需要计算不同深度的延时值,根据延时-叠加算法的原理,图像中同一深度上各个采样点的延时模型是完全一致的。如图2所示,第i行上的点L_i1和L_i2处在同一深度上,它们在各个对应通道中的延时完全一致(在图中用相同的色块表示),可以共享2R+1个延时值,2R+1是波束合成接收孔径的大小。因此,同一深度的各个采样点可以通过共享一组延时值,实现并行合成。再分析同一通道不同深度的采样点,可以发现不同深度的采样点在进行合成时是相互独立的。同样如图2所示,第i行和第j行的采样点在叠加计算时互不影响,也可以实现并行合成。不同深度点的延时值不同,在图中由不同灰度的方块表示。
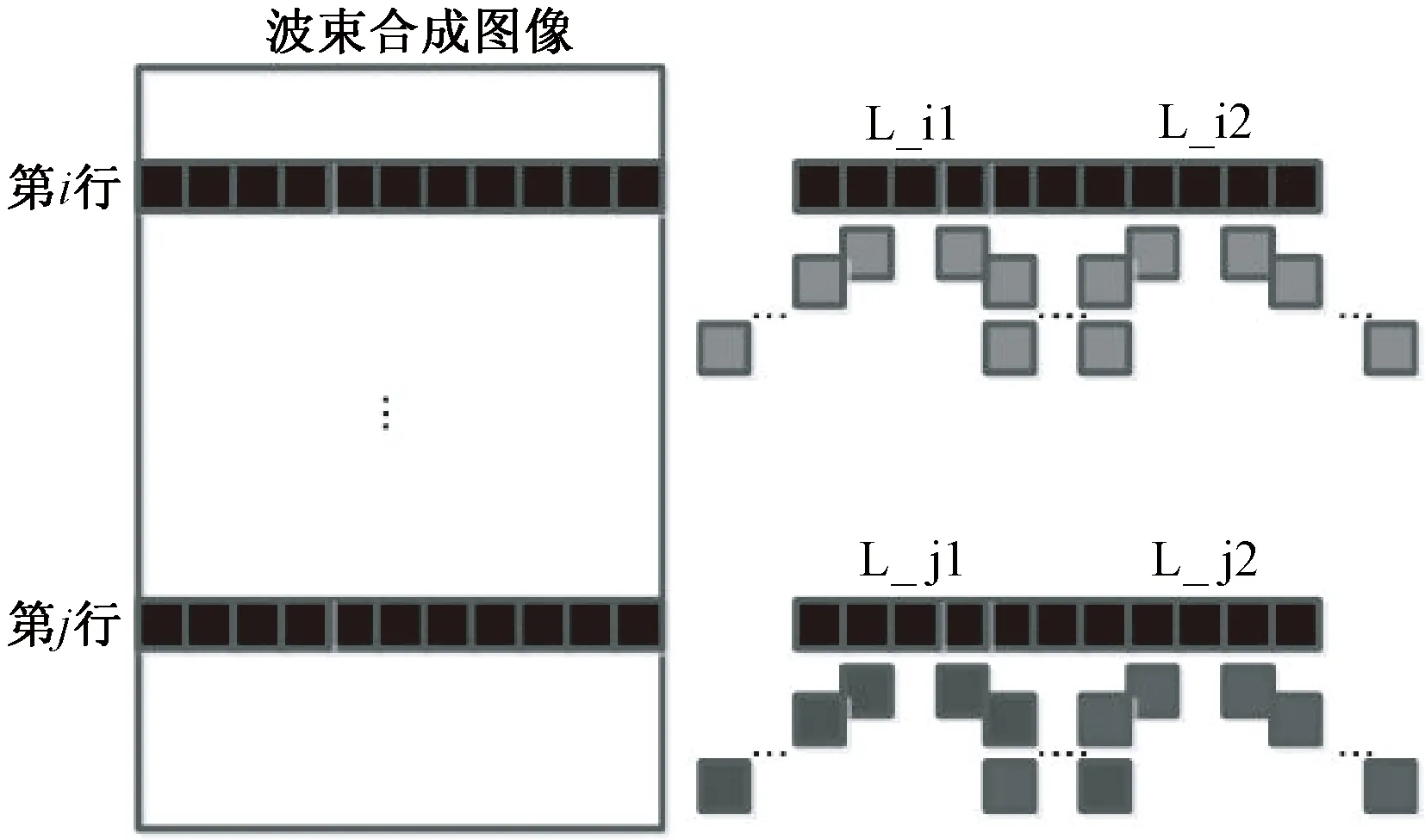
图2 延时-叠加波束合成算法并行性分析Fig.2 Analysis of parallel Computation in delay-and-sum beamforming
通过分析可知,延时-叠加波束合成算法至少存在着两层可并行计算的环节。
1.2.2 2个Kernel实现并行波束合成
由于延时的计算和采样点本身的值没有关系,因此在波束合成前,可以先并行地计算出所有的延时,得到延时表,它的每一行代表了对应深度采样点所共享的一组延时值。在波束合成过程中,对于每个采样点的所有延时不需要重复计算,而是通过“查找延时表”的方式,找到与之同一深度的所有延时值即可。
通过分析可以发现,延时表的计算过程存在着两层的并行,因此可以将延时表的计算作为并行任务1。将任务1交给一个Kernel函数进行计算,此处将该函数命名为Kernel1,通过计算得到的延时表存放于GPU中,供后面的叠加环节使用。
将查延时表进行波束合成的环节作为并行任务2,并建立一个新的Kernel函数执行,该函数此处命名为Kernel2,通过它读取延时表的对应数值进行波束合成,Kernel1和Kernel2各自的Grid和Block设计及并行计算任务的划分示意如图3、4所示。
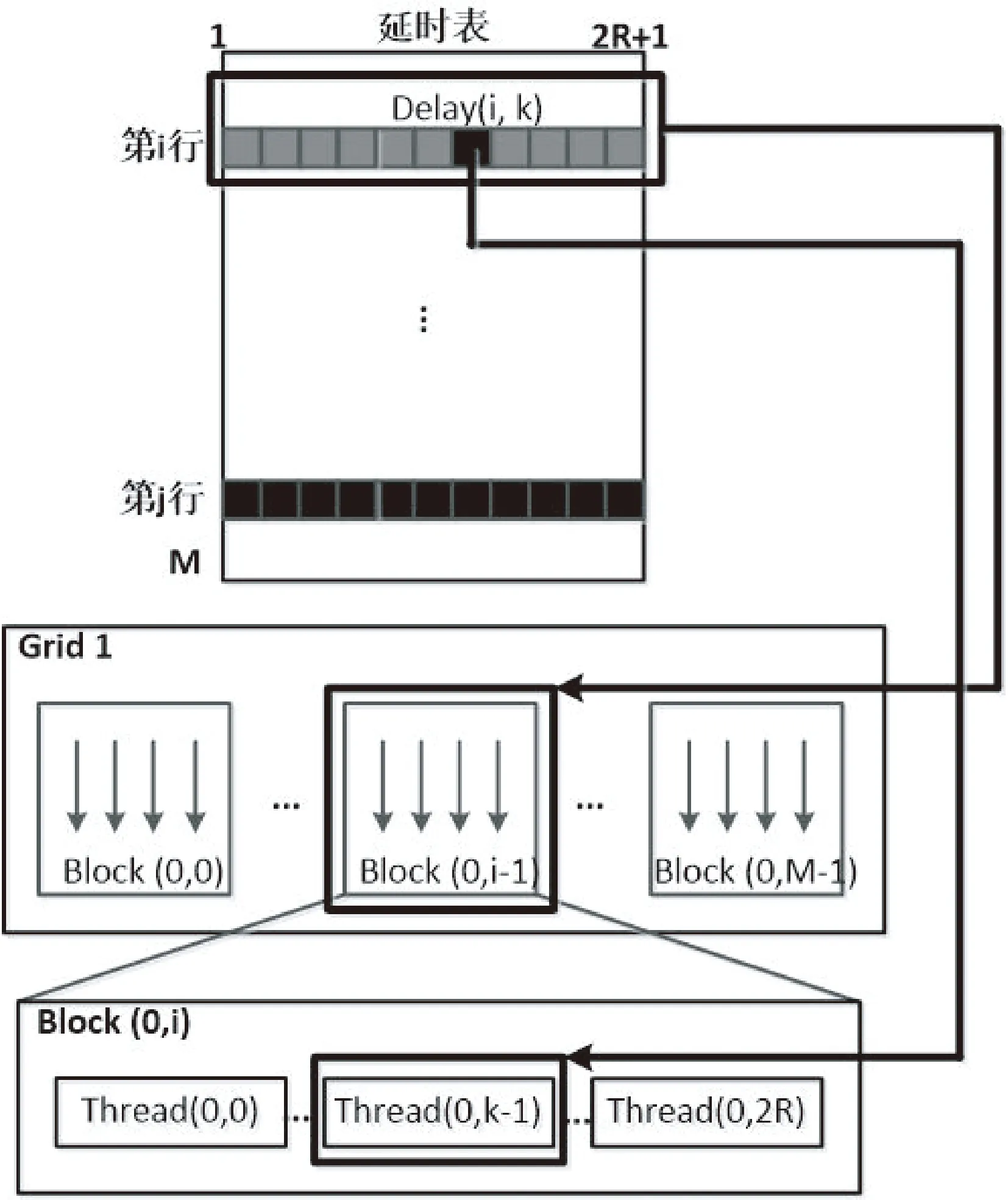
图3 Kernel1对应的Grid1和Block1设计及并行任务划分Fig.3 Diagrammatic sketch of Grid1 and Block1 designs and task assignments in Kernel1

图4 Kernel2对应的Grid2和Block2设计及并行任务划分Fig.4 Diagrammatic sketch of Grid2 and Block2 designs and task assignments in Kernel2
从图3中可以总结出计算延时表的Kernel1过程中的两层并行:
1) 延时表中第i行的2R+1个延时值,全部交给Grid1里的Block(0,i-1)进行计算;
2) 该行的第k个延时值(共2R+1个),则交给Block(0,i)里的Thread(0,k-1)线程进行计算。
从图4可以总结出进行叠加计算的Kernel2过程中的3层并行:
1) Grid2中第s行的M+1个Block负责计算图像数据包中的第s张未合成图像;
2) 这M+1个Block与第s张图像的M+1行数据一一对应,即Block(s, i)负责计算第s张图像的第i行上的所有N+1个像素点的值;
3) 第s张图像的第i行上的N+1个数据与Block(s,i)里的N+1条线程一一对应,即Thread(0,j)负责合成第s张图像的像素点P(i,j)。
1.2.3 1个Kernel实现并行波束合成
使用2个Kernel实现延时-叠加波束合成将 “计算延时”变成更加方便的“查找延时”,但是“查找延时”的设计存在着局限性。首先,查延时表的操作要求对应于每一个接收孔径的延时模式是完全一致的,这仅适用于平面波成像中的无角度偏转发射/接收模式,若采用带角度偏转发射/接收的平面波成像方式,其延时模式更加复杂,因此难以使用该方法,而平面波成像为了提高横向分辨率,通常需要采集多个偏转角度的图像进行多角度空间复合。其次,在2个Kernel的方法中,Kernel1函数算出的延时表只能存放于全局存储器中,而线程对全局存储器的访问存在着几百个时钟周期的延迟,相比于共享存储器、寄存器等,访问速度很慢,这在一定程度上也影响了并行波束合成的速度。
为了改善2个Kernel方法的不足,在改进的方法中利用Kernel2里已经分配的线程来直接计算延时,因为GPU里分配的线程都是轻量级线程,因此单条线程的计算能力并不突出,如果将庞大的计算量分配给若干条线程来计算,会极大地拖慢程序的运行速度。同时,需要为计算得到的延时值设计合理的存储策略,让其他的线程在进行叠加计算时能够达到较高的访问速度,保证1个Kernel的方法也能够保持相同的计算能力。
利用1个Kernel实现延时-叠加波束合成,需要用到GPU中的共享存储器,之所以在2个Kernel的方法中不使用共享存储器,是因为Kernel2在运行过程中,一条线程访问延时表所在的存储器并读取相应的延时值的次数只有一次,不存在一条线程对一个延时值重复读取的情况,因此在2个Kernel的方法中使用共享存储器并不会提高波束合成的速度。
使用1个Kernel实现延时-叠加计算的Grid和Block设计及并行任务划分如图5所示。
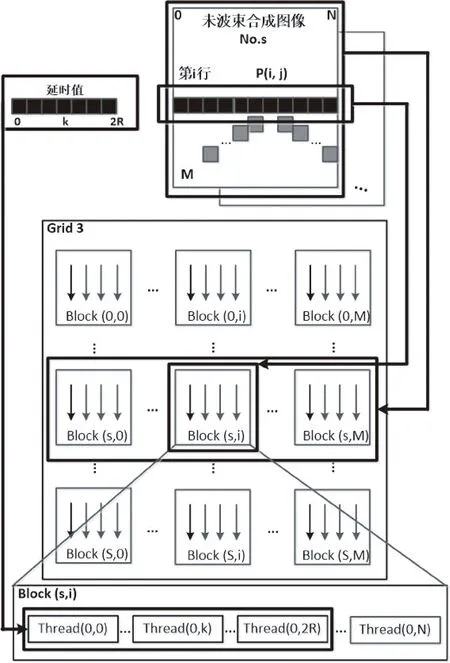
图5 1个Kernel并行波束合成对应的Grid和Block设计及并行任务划分Fig.5 Diagrammatic sketch of grid and block designs and task assignments in beamforming with one kernel
在改进的方法中舍弃了Kernel1,在Kernel2已经分配的线程中分配一部分线程来计算延时值,并将计算得到的延时值存入共享存储器中,避免了将延时值存放在访问速度较慢的全局存储器中。在改进Kernel2中,一个Block的任务是对同一个深度的N+1个数据进行波束合成,并且同一个深度的N+1个数据在波束合成时共用2R+1个延时值。因此在划分并行任务时,分配Kernel2的每一个Block里的2R+1条线程来并行地计算这个Block所对应深度的2R+1个延时值,再并行地将这些延时值存放于所在共享存储器中,经过同步机制后,Block里的所有线程进行叠加计算时,只需要从各自的共享存储器中读取相应的延时值并使用即可。这样的任务划分相比于前者,线程访问读取延时值的速度更快、效率更高。实验结果也证明,尽管Block里有一部分线程因为计算延时值而增加了计算负担,但因为使用了访问速度更快(相比于全局存储器)的共享存储器,波束合成的速度并没有降低。
1.3 实验设计
在仿体实验中,使用Verasonics V-1超声数据采集系统和L11-4线阵探头采集通道数据,探头中心频率7.5 MHz。实验中进行对比的波束合成处理器分别是Intel公司的Xeon CPU(主频3.10 GHz)和NVIDIA公司的Tesla K20c GPU(2 496个CUDA核,5 GB内存),采集通道RF数据的各项参数如表2所示。为了验证GPU波束合成结果的正确性,对合成的结果没有进行滤波、角度复合等优化,因此获得的图像有较强的噪声干扰,对比度和信噪比也不及一般的超声图像。其中,接收孔径33代表合成每一个像素点时用到的通道数,接收孔径大小为9.5 mm。

表2 线阵探头采集通道RF参数及波束合成参数
1.4 评价方法
本研究中对于实验结果的评价方法如下:
1) 均方误差。用归一化的均方误差来评估波束合成结果的正确性,其表达式如下:
(2)
式中:xi,j是参考数据集,在本研究中是采用传统波束合成方法得到的图像矩阵;yi,j是实验数据集,在本研究中是采用GPU波束合成方法得到的图像矩阵;N是数据集的大小;mean(xi,j)表示求平均计算。
2) 计算时间。将超声采集系统获得的100帧通道数据进行打包处理,再一次性送入波束合成器(CPU或GPU)中,计算波束合成器采用不同方法合成完毕100帧图像的时间,以此作为衡量波束合成器计算性能的依据。
3) 算法复杂度和计算量。从算法本身的复杂程度对比,以及不同算法合成100帧图像时所需要的计算量,对3种不同的方法进行讨论。
3 结果
仿体实验的结果如图6所示,其中图6(a)是采用普通串行算法计算得到的B模式图像,图6(b)是采用GPU并行算法中的2个Kernel方法计算得到的结果,图6(c)是1个Kernel方法计算得到的结果。
1) 均方误差。以图6(a)作为参考数据集,将图6(b)、(c)分别和参考数据集做均方误差计算,得到的结果均为0.002 5%。
2) 计算时间。普通波束合成方法和两种并行波束合成方法的计算能力对比如表3所示。可以看到,普通方法耗时4 500ms,帧频为22f/s左右。2个Kernel的方法耗时为45.92ms,计算帧频2 178f/s左右;使用1个Kernel的方法耗时40.76ms,帧频达到2 453f/s左右。相比于普通方法,两种并行合成方法分别加速99倍和111倍。相比2个Kernel的方法,1个Kernel的方法又进一步提速12.68%。
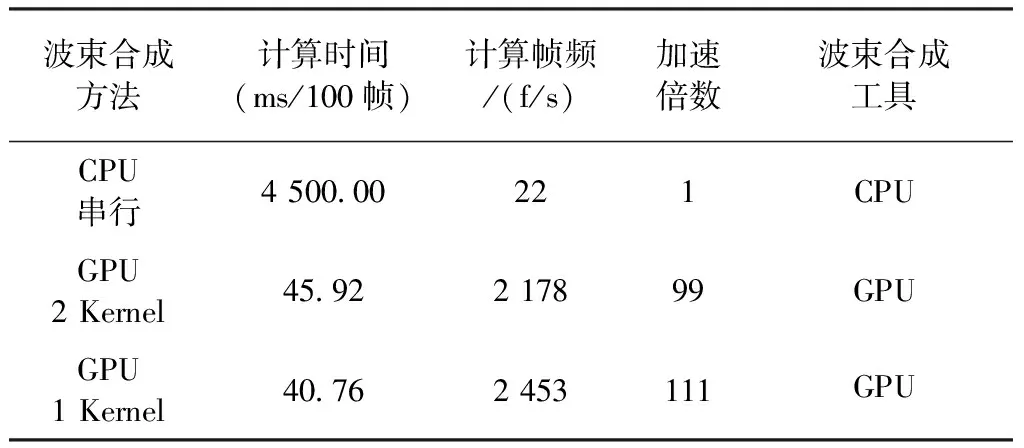
表3 GPU并行波束合成和普通波束合成方法计算能力对比
4 讨论
4.1 算法复杂度和计算量
基于CPU串行计算的波束合成方法在合成每一个像素点时,需要分别计算这些像素点的延时值,再进行叠加计算。对于待合成图像中的每一个像素点,需要循环重复上述过程。本研究提出的第2种GPU波束合成方法,即基于1个Kernel的方法,从算法复杂度的角度而言,和基于CPU串行计算的方法类似,即在合成每一个像素点时,该点的延时值是单独分别计算和储存的,不同的是后者将该方法进行了并行化处理,并利用共享存储器来提高存储效率。综合言之,这两种方法的计算思路是一致的,但基于GPU的方法需要考虑并行分配线程和数据的存储策略。
本研究中提出的基于2个Kernel的方法,需要先建立1个Kernel来计算延时表并储存在全局存储器中,再由第2个Kernel调用。从算法角度而言,该方法的复杂度相对较高,而且相比1个Kernel的方法,更多地利用了全局存储器,因此在一定程度上降低了数据的读取效率。
从数据量的角度考虑,基于CPU串行计算的方法和两种基于GPU并行计算的方法,其数据的输入量和输出量是相同的,其中输入是100帧的通道数据,输出是100帧波束合成之后的射频数据(数据格式也相同)。从中间生成的临时数据而言,基于CPU的方法和基于GPU的1个Kernel的方法在合成每一个像素点时,只会产生对应于该点的延时值数列,存储于共享存储器中并随着波束合成的进行而不断更新。而基于GPU的2个Kernel的方法在计算过程中会产生一个延时表,它会根据图像矩阵的大小而占据不同的存储空间。
4.2 应用灵活性
使用2个Kernel的方法需要先计算出延时表,是基于无角度偏转发射/接收模式的平面波成像在同一深度处有完全相同的延时模式而采用的简便算法,它所适用的成像方法范围较窄,因此当遇到角度偏转发射/接收模式的平面波成像或者是其他先进成像方法时,这样的方法使用并不方便。而1个Kernel的方法通过分配出部分线程直接计算所在的线程块所需要的延时值,提高了应用的灵活性。
4.3 创新和不足
上述两种方法与已有的并行波束合成算法相比,不同之处在于,现有并行波束合成方法一般是同时对不同通道的RF数据进行波束合成,而本研究所采用的方法考虑到了延时-叠加波束合成算法在同一深度上具有相同的延时模式,可以共享一组延时值,从而实现同一个深度上的并行波束合成。在大部分超声图像中,纵向上一个通道的采样点数要远远大于横向上的通道数,该方法并行地合成各个深度上的数据,相比现有的并行波束合成方法,具有更大的加速潜能。
在本研究中,根据延时值计算和存储策略的不同,设计并实现了两种基于GPU的并行波束合成方法,两种方法最大的区别是对共享存储器的使用。由于不同GPU的共享存储器空间存在一定的差别(一般为48 KB),因此采用第二种方法时需要考虑具体所使用的GPU共享存储器大小,避免发生数据的溢出,导致计算结果错误。
该项工作还有可以进一步改进和突破的地方,如进一步优化数据在GPU中的存储策略,减少待波束合成数据因存放于全局存储器中而造成的较高的访问延迟。另外,加入角度复合之后,数据量的成倍增加会导致计算帧频的相应降低,如何保证GPU波束合成器在数据量增加的情况下仍然保持较高的计算能力也是今后工作的重点之一。
5 结论
本研究基于延时-叠加波束合成算法的并行性分析,设计出了两种基于GPU并行计算的超声波束合成方法——基于2个Kernel和基于1个Kernel的并行波束合成方法,并分别编程实现。两种方法均达到了较高的计算能力,相比普通的合成方法大幅度提高了计算帧频。
[1] Bruneel C, Torguet R, Rouvaen KM, et al. Ultrafast echotomographic system using optical processing of ultrasonic signals[J]. Applied Physics Letters, 1977, 30(8): 371-373.
[2] Delannoy B, Torguet R, Bruneel C, et al. Acoustical image reconstruction in parallel‐processing analog electronic systems[J]. Journal of Applied Physics, 1979, 50(5): 3153-3159.
[3] Shattuck DP, Weinshenker MD, Smith SW, et al. Explososcan: A parallel processing technique for high speed ultrasound imaging with linear phased arrays[J]. The Journal of the Acoustical Society of America, 1984, 75(4): 1273-1282.
[4] Lu J, Greenleaf JF. Pulse-echo imaging using a nondiffracting beam transducer[J]. Ultrasound in Medicine & Biology, 1991, 17(3): 265-281.
[5] Tanter M, Fink M. Ultrafast imaging in biomedical ultrasound[J]. IEEE Trans Ultrasonics, Ferroelectrics, and Frequency Control, 2014, 61(1): 102-119.
[6] Souquet J, Bercoff J. Ultrafast ultrasound imaging[J]. Ultrasound in Medicine & Biology, 2011, 37(8): S17.
[7] Montaldo G, Tanter M, Bercoff J, et al. Coherent plane-wave compounding for very high frame rate ultrasonography and transient elastography[J]. IEEE Trans Ultrasonics, Ferroelectrics, and Frequency Control, 2009, 56(3): 489-506.
[8] 夏春兰, 石丹, 刘东权. 基于 CUDA 的超声 B 模式成像[J]. 计算机应用研究, 2011, 28(6): 2011-2015.
[9] So HKH, Chen J, Yiu BYS, et al. Medical ultrasound imaging: To GPU or not to GPU? [J]. IEEE Micro, 2011, 31(5): 54-65.
[10] Yiu BYS, Tsang IKH, Yu ACH. Real-time GPU-based software beamformer designed for advanced imaging methods research[C] // 2010 IEEE International Ultrasonics Symposium (IUS). San Diego: IEEE-UFFC, 2010: 1920-1923.
[11] Yiu BYS, Tsang IKH, Yu ACH. GPU-based beamformer: Fast realization of plane wave compounding and synthetic aperture imaging[J]. IEEE Trans Ultrasonics, Ferroelectrics, and Frequency Control, 2011, 58(8): 1698-1705.
[12] Chen J, Yiu BYS, So HKH, et al. Real-time GPU-based adaptive beamformer for high quality ultrasound imaging[C] // Clemens Ruppel, Ken-ya Hashimoto, eds. 2011 IEEE International Ultrasonics Symposium (IUS). Orlando: IEEE, 2011: 474-477.
[13] Cook S. CUDA Programming: A Developer′s Guide to Parallel Computing with GPUs [M]. Waltham: Elsevier, 2012.
[14] Farber R. CUDA Application Design and Development [M]. Waltham: Elsevier, 2011.
[15] Kirk DB, Wen-mei WH. Programming massively parallel processors: a hands-on approach [M]. Waltham: Elsevier, 2012.
[16] 张舒, 褚艳利. GPU 高性能运算之 CUDA[M]. 北京: 中国水利水电出版社, 2009.
Ultrasound Beamforming Based on GPU Parallel Computation
Chen Yinran1,2He Qiong1,2Luo Jianwen1,2*
1(DepartmentofBiomedicalEngineering,SchoolofMedicine,TsinghuaUniversity,Beijing100084,China)2(CenterforBiomedicalImagingResearch,TsinghuaUniversity,Beijing100084,China)
The conventional line-by-line focused mode restricts the improvement of frame rate in ultrasound imaging. In plane wave imaging, each image is obtained by only one transmission and reception, and thus ultrafast imaging can be achieved. However, the current beamformers cannot meet the demand of ultrafast ultrasound imaging for massive computation. In this paper, the feasibility analysis of parallel computation in delay-and-sum beamforming algorithm was performed and two beamforming methods based on graphics processing unit (GPU) parallel computation including the 2 Kernel-based and 1 Kernel-based parallel beamformers were designed and implemented. The main differences between these methods were the calculations and data storage strategies of time delays in beamforming. Phantom experiments demonstrate that the computational frame rates of each method was 2,178 frames per second and 2,453 frames per second, respectively. Each of the methods obtained a speed up ratio of 99 and 111 compared to the normal method, which demonstrated that the GPU-based beamformer could significantly improve the calculating capability.
ultrasound imaging; beamforming; parallel computing; GPU
10.3969/j.issn.0258-8021. 2016. 06.006
2016-03-21, 录用日期:2016-06-23
国家自然科学基金(61271131);高等学校博士学科点专项科研基金(20130002110061)
R318
A
0258-8021(2016) 06-0677-07
*通信作者(Corresponding author), E-mail: luo_jianwen@tsinghua.edu.cn
